基于高斯估算的多智能体最优覆盖控制网络研究
2020-12-24李晶
李 晶
(辽宁工程职业学院,辽宁 铁岭 112008)
0 引言
现实环境会发生各种各样预想不到的灾难,例如地震、火灾、洪涝灾害等,这些灾害发生后会产生相对比较复杂的灾难环境,如高风险、高污染性、次生灾害随时存在等等,这样的环境对人类开展救援非常困难。因此,开发具有自主性的智能机器人来代替自然人来执行救援任务成就成为迫切的需求。复杂的灾后动态环境,智能机器人个体是无法独立完成任务,这就需要多个智能机器人个体组成的多智能体系统相互之间协同互助共同完成设置的各项任务,输出误差也能够在控制范围内。在灾难救助过程中,很多目标任务都具有不可预测性,多智能体系统需要有更强的感知能力、移动和信息传导能力[1-2]。在实现某些特定的任务的时候,需要对特定任务环境和要求进行实时监控,并且综合各种因素较好的完成任务。那么如何解决多智能体与外部综合因素之间的互动,这是多智能体的最优覆盖控制很好地应用。
1 多智能体最优覆盖控制方法
多智能体在特定区域内的最优覆盖控制行为,本文把这种特定区域可以成为多智能体所要执行任务的目标区域。笔者针对不同的智能体对目标区域进行分割,对单个智能体在所处区域内进行控制,在通过整个覆盖系统的感知能力和信息传导能力将其控制信息传导给其他的智能体,同时各个智能体之间还能相互监控,进而实现对目标区域的最优监控目标。根据目标区域内被关注信息的分布(敏感度函数),合理地分布多智能体,使目标区域中需要重点关注的区域拥有更多的执行任务的智能体,从而获得更多的参数,为下一步实施监控提供有力支撑。
1.1 高斯估算
在通常情况下,现实研究的智能体所处的目标区域内的敏感度函数是未知的,由于敏感度函数未知,为了解决多智能体覆盖控制问题,首先要有效获得多智能体覆盖网络即目标区域的各采样信息,然后对获得各种采样信息进行数学描述,同时利用高斯估算对其进行寻优。
1.1.1 数学描述
假设目标区域内有n个智能体随机分布没有任何规律,那么将各个智能体的位置信息用下列算式表示:
(1)
其对应的运动表达式如下所示:
(2)
上式中,ui为第i个智能体的控制输入。
根据随机变量的取值参数估计,假设每个智能体的损失函数均表示为f(pi,q)=‖pi-q‖2,因此多智能体覆盖网络总的损失函数为:
(3)
得到敏感度函数为:φ(q):R2→R+。
每个智能体的控制输入为:ui=ki(Cvi-pi),i=1,...,n。
1.1.2 高斯估算
在覆盖网络中不同区域的敏感度函数常被用于描述该区域内的一些属性,如温度、湿度等,且这些信息不会随时出现急剧变化,但由于区域的复杂性这些属性也处于一种没有界限的情况。因此,利用估算的基函数κ(q)和权重系数β以组合的形式,即:
(4)
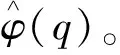
(5)
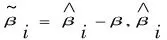

1.2 最优覆盖控制方法
由于目标区域内的敏感度函数的不确定性,需要在(tk,tk+r)时间内,对智能体在目标区域内的敏感度函数特定时间值进行信息采集。采样间隔为hk=tk+1-tk,则其在估计系统中的采样数据集合可以通过下式表示,即:y=[yNi(tk)T,...,yNi(tk+r)T]T。因此,覆盖网络内智能体数据采样集合为D={P,y}。
因其敏感度函数估计系统的基函数κ(q)=[K1(q),...,Km(q)]T,在上式中引入向量系数β,使得上面提到的数据采样集合D满足y=κ(P)Tβ,具体表达式如下:

(6)
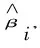
(7)
因此,多个智能体对目标区域内敏感度函数估计值为:
(8)
(9)
(10)
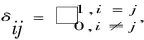
(11)
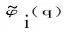
(12)
假设覆盖网络的代价函数具体形式为:
(13)
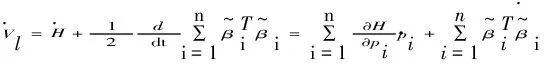
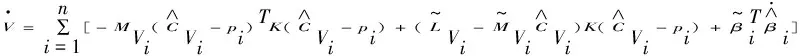
(14)
(15)
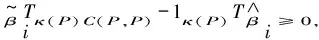
2 结语
基于高斯估算的最优覆盖控制网络研究,文章提出一种多智能体,主要利用了智能体所处目标区域未确定的敏感度函数进行数据采样,给出了其最优信息分布方法,即估计值与实际应用之误差在实际控制范围内,使得多智能体在目标区域内近似于最优分布。
