雷达伺服系统全阶磁链观测器设计与实现

徐俊

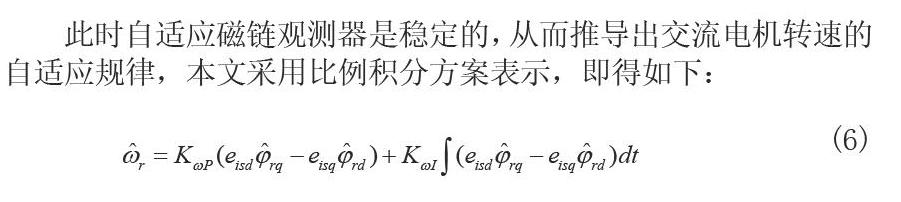
摘要：针对自适应速度辨识系统不稳定问题，本文构造了一种全阶磁链观测器，实现了交流电机速度估算，建立了雷达伺服系统速度回路。利用TMS320F2812建立了硬件实验平台，实验表明雷达伺服系统全阶磁链观测器在低速时能够稳定运行，对电机参数变化和外界干扰有一定自适应能力。

关键词：雷达伺服系统;全阶观测器;Lyapunov

1  前 言

伺服系统是雷达的重要组成部分，特别是在交流伺服系统设计中，交流电机因其结构简单、运行可靠、可维修性、互换性以及经济性好等优势，一直受到广泛关注。随之而来交流电机控制理论、方法也逐渐进入实用阶段。

本文根据状态观测理论，提出了一种全阶自适应磁链观测器，运用稳定性理论Lyapunov实现了交流电机转速和定子电阻估计，建立了无速度传感器雷达交流伺服系统。

2  全阶状态观测原理

全阶观测器就是构造一个状态观测器，其维数与实际系统的维数是接近或者近似相等的。提供全阶观测器与实际系统同样的条件要求，从而实现估计的输入和输出量可以代替真实而难以得到的输入和输出。

定义一个系统：

其中输出量 、输入量 是可以直接得到，但是中间状态量 是不能被直接观测的。全阶状态观测器就是利用可以直接得到的 和 ，去估计出与实际状态量 近似相等的 。

3  交流电机全阶磁链观测模型

以定子电流 和转子磁链 作为状态变量，在α-β坐标系下交流电机模型的状态方程可以表示为[4]：

（2）

从上述描述的交流电机状态方程和状态观测器原理可知，取定子电流 和转子磁链 作为观测量，构建适合的增益矩阵G，以此形成交流电机全阶磁链观测器模型，具体表达式如下所示：

（3）

式中，^为估计值。

增益矩阵G的选择对系统稳定性和抗干扰能力有一定影响，实际设计中，增益矩阵G可以参考观测器极点与系统极点之间的关系。

4  基于Lyapunov理論的电机参数辨识

为了推导出自适应规律，本文运用了稳定性理论Lyapunov，将式（1）作为参考模型，式（3）观测器作为可调模型，其中式（3）观测器中含有交流电机转速和定子电阻的辨识值 和 。式（3）与式（1）相减得到关于定子电流和转子磁链的观测误差状态方程：

（4）

式中：

运用Lyapunov函数，选择适当增益矩阵G，使得下式，即：

此时自适应磁链观测器是稳定的，从而推导出交流电机转速的自适应规律，本文采用比例积分方案表示，即得如下：

（6）

式中，比例系数均为正数，值的大小与观测器的响应速度有关。

5  交流伺服系统全阶磁链观测器的实现

根据系统设计要求，利用TMS320F2812建立了基于全阶磁链观测器的交流伺服系统，如图4所示。结合硬件实验平台，进行了相关控制软件设计。

6 实验结果

利用上述建立的雷达交流伺服控制系统实验平台，对全阶观测器原理进行了验证。 图5为电机一定转速下，全阶观测器估计的电机转速曲线，由上述可以看出，伺服系统具有较好的稳定性和动态响应能力。

7 结 论

本文由状态观测理论延伸建立了一种自适应磁链观测器，运用稳定性理论Lyapunov实现了电机速度估算，构成了雷达伺服系统速度回路。利用TMS320F2812建立了仿真实验硬件平台，仿真实验验证了雷达交流伺服系统全阶自适应磁链观测器的有效性和鲁棒性。

参考文献：

[1]李忱.无速度传感器雷达交流伺服系统设计[J].现代雷达，2002，11（6）：78-81.

[2]王坚，年晓红，桂卫华，曹霄.新型异步电机无速度传感器控制方法[J].中国电机工程学报，2008，3（28）：96-101.

[3] Yang G，Chin T H.Adaptive-speed identification scheme for a vector-controlled speed sensorless inverter-induction motor drive[J].IEEETrans on Industry Applications，1993，29（4）：820-825.

[4]Kubota H，Matsuse  K.DSP-based adaptive flux observer of induction motor[J].IEEE Trans on Industry Applications，1993，29（2）：344-348.