在计算教学中利用迁移学习提高学生的运算能力

邢锦竹

摘 要：在小学数学计算教学中，积极地运用迁移规律，利用学生已有的计算知识和技能对新知识、新技能的学习产生积极的影响，进行重组建构、拓展延伸，就可以把整个计算相关的算理、算法串联起来，形成完整的认知结构，提高学生的运算能力。

关键词：计算教学;迁移学习;运算能力

一、课前微课学习，沟通前后知识之间的联系，进行初步迁移

大家都知道，迁移所依赖的主要条件是不同知识存在着共同的因素，前后教材的共同因素越多，就越容易产生正向的迁移。在学习新知识时，通过发掘新旧知识的共同因素，并充分利用这些共同因素，创设迁移情境，就可以沟通新旧知识的内在联系，逐步提高学生学习和探索新知识的能力。

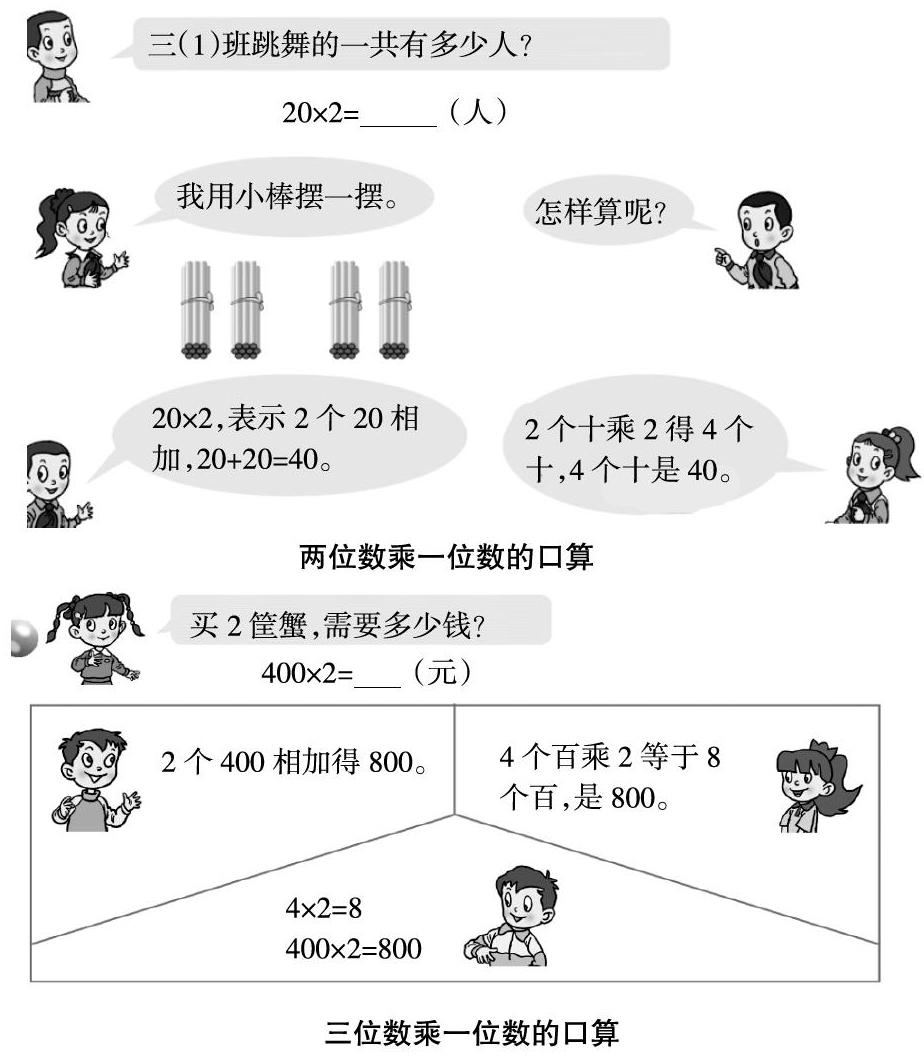
例如：青岛版三年级上册将“两位数乘一位数”“三位数乘一位数”分成前后两个单元，教材这样设计一来可以分解知识难点，二来可以引导学生利用知识迁移，“拾级而上”，逐步理解口算算理，掌握口算方法。

从教材中可以看出，对于两位数乘一位数的口算素材的呈现，教材提供了摆一摆、转化成加法、利用数的意义说理、根据以前的乘法口诀进行推算等不同的方法，帮助学生在从不同角度理解算理的基础上掌握算法。三位数乘一位数的口算与两位数乘一位数的口算在算理、算法上完全相通，对于三位数乘一位数，可以在学生拥有的两位数乘一位数的学习经验基础上进行迁移类推，自主探索算理形成。教材阶梯上升的设计，有助于培养学生的运算能力。

在教学“三位数乘一位数口算”时，教师可以制作两位数乘一位数口算的预习微课视频。学生课前观看微课，联想起以前学习过的两位数乘一位数的口算方法的探究过程。在已有知识经验的基础上通过迁移类推，自主探索学习三位数乘一位数口算的方法。在这个学习过程中，学生能尝试沟通口算的算理和算法，并利用已有的知识经验解决类似的新问题，促进了运算能力的发展。

二、课堂交流分享，沟通算理优化算法，实现迁移后的提升

在学生课前自学微课、初步探索的基础上，课堂进行交流分享。学生探索到多种不同的解题思路，通过小组内和全班范围的解析、提问、补充，进一步完善了学生的认知，使学生更深入地理解了三位数乘一位数口算的算理。

例如：青岛版三年级上册第三单元“三位数乘一位数的口算”一课中有这样的片段：

师：计算400×2时联想起哪些以前学过的知识，用到过的方法，自己又是怎样用这些经验去研究计算400×2的？

生1：以前我在两位数乘一位数的口算中用了摆一摆的方法，我现在也用摆一摆的方法。我在百位上先摆4个珠子，表示400，又摆4个珠子表示400，两个400就是800，所以我认为400×2=800。

生2：我也是用摆一摆的方法，但是我用小方块来摆。一个大方块表示100，我先摆400，再摆400，一共是800，所以400×2=800。

生3：我是把乘法转化成加法400+400=800，所以400×2=800。

生4：我是这样想的：4个百乘2得8个百，就是800，所以400×2=800。

生5：以前我們学过4×2=8，我在做40×2=80，所以400×2=800。

师：同学们想到了这么多办法，有摆一摆、有转化成加法、有的把400看成4个百，这些方法都可以求出400×2=800。想一想，这些方法之间有什么联系啊？

生1：画图和加法有联系。

生2：图和看成几个百有联系。

生3：看成几个百和推算有联系。

师：同学们真善于思考，虽然每种方法看起来都是不同的，但它们的道理是相通的。

在学生交流分享学习成果后，教师引领提升。先和学生一起将多种方法进行梳理，然后引导学生通过观察、比较，体会到所有的方法在道理上都是相通的，从横向上建立各种方法之间的联系，更进一步地明晰口算算理。

在接下来大量的口算练习过程中，学生自然而然地选择了更加简洁的算法，从而实现算法优化。在此基础上，教师及时点拨，理清算理和算法之间的关系，逐步突破教学难点，学生的思维也经历了一个充分感悟—自然碰撞—理性提升的过程。

三、挖掘练习内涵，在应用知识的过程中进一步迁移拓展，促进运算能力的发展

教学活动中的各种练习，是学生应用知识的一种重要形式。这种知识的应用，同知识、能力的迁移有着密切的关系。所以教师要重视练习的设计，充分挖掘教材练习题的内涵，进一步利用迁移规律提高学生应用知识解决问题的能力，并注意在练习的过程中适时适度地进行拓展，为后续学习中的进一步迁移做好准备。

在“三位数乘一位数的口算”一课的练习环节，为了进一步培养学生利用知识的迁移进行学习，并提高运算能力，教师特意做了以下的练习设计，目的是在巩固三位数乘一位数口算方法的基础上，引导学生将两、三位数乘一位数的口算方法继续迁移到四位数乘一位数、五位数乘一位数，甚至四位数乘两位数中，让学生的学习结构清晰，会运用知识的迁移来解决新问题，并为今后的学习打下基础。

例如：青岛版三年级上册第三单元“三位数乘一位数的口算”一课中有这样的片段：

师：仔细观察第一栏，你有什么发现？

再看看其他几栏，是不是也有这样的规律？

生1：每组都是乘的第一个数字。

生2：后面的题比前面的题多1个0。

生3：一个因数扩大了10倍，结果也扩大了10倍。

师：你们的意思是不是先算2×3，然后呢？

生：因数有几个0，就在后面添几个0。

师：那500×4的结果为什么有3个0？

生：因为本身5×4就有一个0了，然后500后面有2个0，这样就一共三个0。

将口算方法拓展到四位数乘一位数。

师：我想考考大家，出示算式2000×3，你会算吗？追问：你是怎样计算的？

生：2000×3=6000，先算2×3=6，然后2000后面有三个0，就在6的后面加三个0。

师：谁能像老师一样出一道题考考大家？

引导学生自主提问，自主解答，给学生提供想象和思考的空间，将知识继续迁移。

在这个环节中，引导学生通过观察、比较，发现规律，打通两位数乘一位数口算和三位数乘一位数口算的方法，并尝试将这种方法迁移拓展到更多位数乘一位数的口算中，有效地培养了学生的运算能力。

总之，我们在计算教学中要准确把握教材的设计脉络，了解学生已经具备的计算知识和技能，抓住知识的生长点，创设情境，大胆放手让学生自主探究、类推迁移、自主建构。让迁移成为学生学习的一种思维习惯，引导学生自觉地在计算学习中应用迁移规律来理解算理、掌握算法，并能解决问题，从而提高学生的运算能力。

参考文献：

[1]李旭.如何在计算课中培养小学生的迁移能力[J].新课程（小学），2015（7）：215.

[2]沙丽侠.如何在计算教学课堂中培养小学生的知识迁移能力[J].商，2013（24）：377.

[3]李林娟.浅谈在计算教学中培养小学生知识的迁移能力[J].读写算（教育导刊），2012（18）：11.

[4]唐国富.浅谈在小学数学教学中如何提高学生的计算能力[J].知识文库，2016（6）：135.

编辑 郭小琴