《平行四边形的初步认识》单元整体设计的教学反思

陈枫枫

摘 要：基于单元整体教学设计的设想，苏教版二年级上册第二单元“平行四边形的初步认识”分为直观认识课和操作活动课。直观认识课中集中教学多边形和平行四边形的初步认识，课题为“认识多边形”;操作活动课中通过围一围、拼一拼和剪纸等体会多边形和平行四边形的形状特点，感受相关图形之间的联系，培养动手操作能力，课题为“变化的图形”。单元整体教学设计的理念在于贯通单元每个课时知识之间的联系甚至是单元与后续知识，在整合的基础上，使教学内容在有主线的基础上又能一气呵成。

关键词：平行四边形;单元教学;直观认识课;操作活动课

本文就关联多边形与平行四边形还是突出平行四边形的深入探究、归纳还是演绎、以活动为主还是以讲解为主三个问题进行深入思考，旨在完善教学设计，更好完成教学目标，凸显单元整体教学的优势所在。

一、关联还是突出

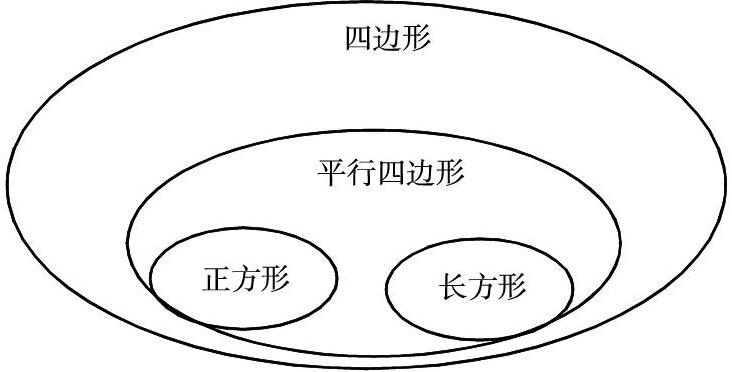
原有教学中关联了四边形与正方形、长方形、平行四边形，如下图四者关系，将已学平面图形做特殊与普遍上的区分与归纳，在学生头脑中建立平面图形的逻辑关系：

此环节仅基于正方形、长方形、平行四边形都有四条边这一共同特点将三者与四边形相联系，但正方形、长方形与平行四边形之间的逻辑关系却并未凸显，这一知识点也是后续学生易混淆的知识点。

二年级的学生如何通过将正方形、长方形归入平行四边形来突出其独有的特点呢？教学中应采取归纳的方法，教学设计如下：

设计三组开火车的动画。

第1个动画，一辆火车从一条铁轨上开过。

师：刚刚你看到了什么？

生：一辆火车从铁轨上开过去了。

师：为什么火车能从铁轨上开过去？

生可自由回答。

然后，教师出示另一条不平行的铁轨，火车开动失败。

师：为什么这里的火车开不了了？

生：因为第1辆火车的铁轨两边是向着同一个方向，而刚刚的铁轨交叉了。

第1个动画，一辆火车从另一条铁轨上开过，和第1条铁轨交叉出平行四边形。

师：这两组铁轨交叉出了什么图形？

生：平行四边形。

师：怎么样的铁轨可以交叉得到平行四边形？

生：两组相交铁轨可以交叉出平行四边形。

第2个动画，两组铁轨交叉得到一个正方形。

第3个动画，两组铁轨交叉得到一个长方形。

师：这三个图形分别叫什么？

生：平行四边形、正方形、长方形。

师：有人说，正方形、长方形也叫平行四边形，你们同意吗？小组讨论一下。

请小组代表发表意见。

总结：因为正方形、长方形也是由同一方向的两条相交铁轨交叉得出，所以它们是平行四边形。

师追问：那么可以说平行四边形是正方形吗？

生：不可以。

师：为什么不可以呢？

生：因为正方形两组对边都是正正的，而平行四边形有一组对边是斜斜的。

同理得到平行四边形也不是长方形。

从生活中常见的铁轨引入，不出示专业词“平行”又能从铁轨两边同一方向的特点感觉到“平行”，两组铁轨相交形成平行四边形，得到大前提——两组对边平行的四边形是平行四边形，而后两组铁轨相交又相继形成正方形、长方形，得到小前提——正方形（长方形）两组对边平行，在学生脑中建立这样形象性的联系，自然而然能得到正方形、长方形是平行四边形的结论。通过追问又得到平行四边形不是正方形、长方形，因此“正方形、长方形是平行四边形”是充分不必要条件。如此循环论证，学生能较好地厘清正方形、长方形与平行四边形的逻辑关系。

二、归纳还是演绎

归纳与演绎是两种不同的逻辑思维方式。原有教学采用演绎法，太过束缚学生的自主思考。正如怀特海所说“为了获得知识，我们首先必须使自己不受知识的束缚”。因此，为了让学生不受束缚地获得知识，采用归纳法教学，可进行如下教学调整：

师：同学们，上节课我们都认识了哪些图形朋友呀？

生：我们认识了四边形、五边形、六边形还有平行四边形。

师：想自己把它们变出来吗？

生：想。

出示一幅钉子板图。

师：我们可以在哪里把这些好朋友变出来？

生：在钉子板上。

师：同桌一起合作在钉子板上先变出四边形、五边形、六边形，好吗？

生自主活动，请一位学生上来展示其作品。

生：我围出了一个四边形、一个五边形、一个六边形。

师：他围得怎么样？

生鼓掌通过。

师：那么四边形的边在哪里？有几条？顶点在哪里？有几个？同桌讨论一下，一人说边一人说顶点。

各组同桌上臺依次说明。

师：回忆刚才多边形的边和顶点的数量，你有什么想说的？

生：四边形有4条边和4个顶点，五边形有5条边和5个顶点，六边形有6条边和6个顶点。

师：发现了什么？

生：是几边形就有几条边和几个顶点，边和顶点的数量相同。

师：现在，请你拿出三角尺（全班三角尺都相同且拼出的三种平行四边形之一是长方形或正方形），这两个三角尺有什么特点？

生：一样的。

师：你怎么证明它们一样呢？

生：可以把它们重叠起来。

师：你能用这两个相同的三角尺拼出一个平行四边形吗？

生自主拼平行四边形，请三个同学分别展示他们拼出的平行四边形。

师：请问怎么把两个相同的三角尺拼成一个平行四边形呢？誰上来说一说。

生：把两个相同的边合在一起，它们两个方向是相反的。

师：这个方法对吗？请你再试一试。

生再试。

师：这个方法有用吗？

生：有。

师：现在请你仔细观察这个平行四边形，上下两边有什么特点？

生：上下两条边是相同的。

师：左右两条边呢？

生：左右两条边也是相同的。

师：你有什么想说的？

生：平行四边形上下两条边、左右两条边是相同的。

师：那如果一个四边形上下两条边、左右两条边是相同的，那它是？

生：是平行四边形。

没有预先提供多边形的样子，学生凭借原有经验围出四边形、五边形、六边形。通过观察，从一个一个特殊多边形所具有的相同的边与顶点的关系得到普遍结论。拼一拼中，学生先用方法证明了两个三角尺是相同的，而后用三种不同的平行四边形（其中一个拼出的是正方形或长方形，正好运用了正方形、长方形也是平行四边形的这一结论）得到同一个拼平行四边形的方法，再用此方法验证，随后追问上下、左右两边的关系，初步体会平行四边形两组对边相等、两组对边相等的四边形是平行四边形。

三、活动为主还是讲解为主

数学中大多新知学习以教师讲授为主。但教育学所关心的是孩子自身及其发展。因此，单元整体教学设计中单独设立一节操作课，大多为学生活动，旨在围图形、拼图形、剪图形等过程中培养学生的空间想象能力，使学生脑中的平面图形可做、可摸。因此，每一操作环节的总结归纳是必要的，且可通过板书来展示此操作活动课的具体知识要点。下文对剪正方形和四边形环节做如下教学设计的调整：

师：在一张正方形纸上剪下一个三角形，剩下的部分是什么图形呢？

生自主剪图形，请剪出不同剩余部分图形的三个学生上来展示并说明。

师：那么一张正方形纸上剪下一个三角形，剩下的部分是？

生：三角形、四边形、五边形。

师：那么，一张四边形纸上剪下一个三角形，剩下的部分是什么图形呢？请你猜一猜？

生：可能是三角形、四边形、五边形。

师：是这样的吗？剪剪看。

生自主剪图形，请剪出不同剩余部分图形的三个学生上来展示并说明。

师：你有什么发现？

生：一张四边形纸剪下一个三角形，剩余部分可能是三角形、可能是四边形，也可能是五边形。

师：回忆刚刚一张正方形纸上剪下一个三角形后剩下的什么？

生：三角形、四边形、五边形。

师：正方形也是什么图形？

生：正方形也是四边形。

师：对这个你有什么想说的？

生：所有的四边形剪下一个三角形后剩余部分可能是三角形、四边形、五边形。

此一环节由剪特殊的四边形正方形开始，再剪随意的四边形，在学生脑中建立“无论特殊还是普遍的四边形，剪下一个三角形后剩余图形都可能是三角形、四边形、五边形”的结论形成过程，由表象内化为抽象结论。

为弥补操作活动课讲解不足的劣势，每一环都应有板书设计，整体板书设计如下：

变化的图形

几边形就有几条边和几个顶点，边与顶点的数量相同。

等边对齐，方向相反。

四边形剪下一个三角形都可能剩一个三角形、四边形或五边形。

通过反思教学中的这三个问题，可知单元整体教学设计不仅贯通知识，更是为学生后续知识的学习作长远铺垫，更尊重学生主体地位。通过环节巧妙设计，由个别到一般，注重每个学生的思维发展水平，获得归纳得到数学结论的乐趣与信心，不拘泥于以往惯有的教学形式，依托教材，更依托教师对基础教育阶段数学知识的整体考量，在系统总结知识要点的基础上采用以活动为主的课程。

参考文献：

[1]怀特海.思维方式[M].北京：商务印书馆，2013：9.

[2]马克斯·范梅南.教学机智：教育智慧的意蕴[M].北京：教育科学出版社，2014：33.

编辑 冯志强