探问，让有效学习真实发生

李增文

教学活动中如何充分调动学生学习的主动性、让学生的思维活动始终处于积极探索的状态中，使数学思维和能力实现从“无”到“优”再到“新”的质的提升，以期达成学习的最大效率，这是数学教师必须冷静思考和积极行动的大课题。

现以“复式统计表”这一教学内容为例，旨在阐明学生数学思维的积极调动、学生学习主动性的深度开掘、学生创造能力的不断突破。我们相信这样的探索不仅操作性强而且有实际的效益。

课前我们分析了学生的学情，知道学生已经具备初步的数据收集、整理、应用等相关的统计经验。因此预设新课教学目标时必须有新的关注点，既要避免重弹老调，又要在知识迁移中做到同中求变、异中出新。建立且问且探式的课堂教学结构模式，既能保证学生理解、掌握统计表的特征等，又能使学生在求同、整合、创造等思维活动中有突破、有成果、有体验，从而达到提高学生数学核心素养的终极目的。

一问：是和盘托出，还是层层剥离？

教材例题是这样引入的：

那我们就如此这般地整体呈现给学生吗？分层出示该怎样实施？哪种方式更能引起注意？哪种方式目的性、方向性更强？哪种方式使学生的注意力更持久？

我们先出示一张古筝统计表。这样学生的注意力就会比较集中，优于出示四张时目标分散，避免了盲目性。随后让学生阅读和理解这张统计表中数据表示的意义，复习一下单式统计表这一旧知识。随后把其余的三张统计表一并呈现，引出下阶段的探索。

从心理角度分析，和盘托出也许得到的只是瞟一眼而已;藏着掖着，反而能吊足观众的胃口，也能增强学生的好奇心、探索欲。从文艺角度分析，“犹抱琵琶半遮面”般出镜，似乎更具有美的欣赏价值。从数学教学有效性的角度分析，做到层次性强、逻辑清晰、前后连贯，才是合理妥帖的。

二探：整合共同点

曾经在一个数学名家的讨论会上听到这样一个议题：小学生数学思维中，是求同思维重要还是求异思维重要？哪个要先行一步？讨论的结果为：“求同思维”重于求“求异思维”;“同”是确定知识的“大类”，是基础，是知识的核心。个人也深信这一点。

四张统计表揭示后，学生的思维进入第二个层面：观察、比较相同点。学生可能还是会停留在信息的介绍这一个层面，但教师要有所控制，切忌投放时间过多，点到为止即可，教师要有方向性地迅速把学生的关注点引向比较它们的“相同点”。教学时要鼓励学生大胆说出自己的想法，紧扣主要特征，善于抓住契机寻找切入点。譬如都有“两行”和“四列”。

此时老师可以追问：如果把四张统计表整合成一张，能不能做到？

继续追问：新的统计表长什么样子？（几列？几行？）

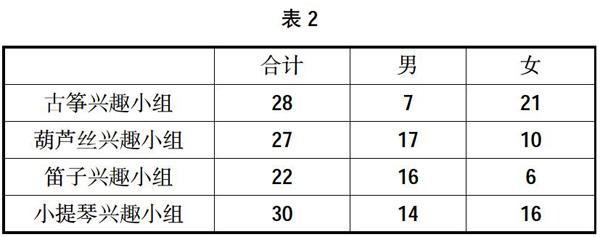
随着老师不断的追问，学生的探索也如剥洋葱般直抵核心：（1）四合一，是可行的;四合一，体现数学的简易美;（2）四列！共性明显，相比很容易得出;（3）几行？两行肯定不够，稍有难度，但“跳一跳”也就能摘到这个“甜果子”了。这样，一个复式统计表雏形就“创造”出来了。学生填上数据，就成了表2。

那么，如果我们就简单地把复式统计表出示给学生，然后指导他们理解表格并填写数据，学习的效果会一样吗？答案不言自明。容易得到的大多没有滋味，辛苦挣得的虽少但金贵。学习活动缺乏了探幽入微的追寻，周折是少了，但思维能力明显缺位，探索也只能止步于浅显的层面，学习的体验终归是平淡的。

三问：是望山即止，还是登顶览胜？

学生填好统计表，顿时幸福感油然而生。但是追寻的步伐才刚刚开启，遥望得到的是同一平面的景致，而最美的风景都是登临巅峰后的所见。

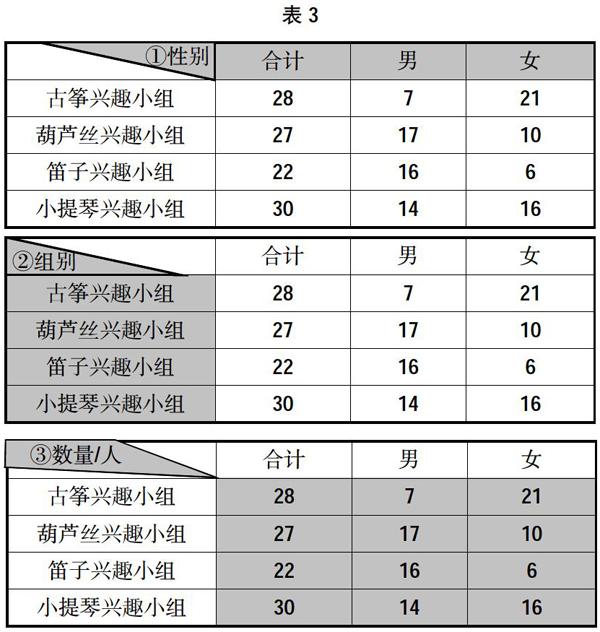
我们可以指导学生按“列”观察表二，从右向左一列列地寻找规律。告诉学生左上的空一格比较特殊，这格叫作“表头”，就是像头脑一样的“指挥中心”;表头一般分成三个部分。同时，教师还能借助媒体，对同一信息作模块化底色处理。这样教学效果会更佳，学生印象会更深，如表3。

这阶段，学生按“列”寻找规律，一般会确定左上角所填“组别”的合理性。这是认知趋同、思维惯性的缘故。那么这种惯性思维如何打破、认知视角如何转换，就需要教师的讲解和引领，这样就能把学生引领上一个新高度。有效教学从不拒绝教师的讲解，教师当讲则讲，要在关键处助力。新知建立又打破，这种持续的建立和打破就使学生的思维有了不竭的动力源，学习活动充满了挑战性，成功感也越能激动人心。最后教师宣告：你们创造的统计表就叫“复式统计表”时，学生沸腾了！

四探：解密奥妙处

这个时候，教师直接出示教材中的复式统计表。学生的高峰体验迅速降温，他们惊呼“怎么不一样”、怀疑“老师别有用心”、自嘲“我们上当了”、恍悟“我们千辛万苦得到的不是对的”……学习的情感体验千姿百态。

教師利用多媒体，清晰地展示两者间的联系过程：把下面四行整体向下移动，在首行下面插入“总计”行。运用底色，增强两者间的不同，如表4。

新鲜的事物总是最能吸引眼球！学生刹那的失落又立刻转移到新的探究中。

老师可以这样问：如果你是设计人员，你会这样设计吗？

面对学生的迷茫，教师适度提问：增加了几个数据？哪些数据你会算？

接下来让学生分组研究讨论，分别算出了男生的总计数、女生的总计数。

最后一个格子，学生尝试了用不同的算法后就能发现：男生数+女生数=四个小组合计数的总和！最后一个数据竟然还隐藏着验算的功能！

追问：你觉得这种设计的妙处在哪里？

这时候，学生都不禁发出感慨：这样设计的复式统计表的信息量更多且更科学！如不好好研究，还真发现不了这些奥秘呢！深度探究，赋予了学生绝妙的、独特的学习体验，同时也让学生领略了数学的迷人魅力！

五问：是双向互通，还是单向练习？

巩固练习阶段，我们采用课本习题，继续利用例题的元素，并注重联系学生的实际，开展调查，收集数据，填写表格，分析数据，完成全部的操作。

老师问：刚才的例题中提到了四种乐器，如果从这些乐器中选择一种，你想学习哪一种？（学生自由交流，将自己的答案写在小纸条上。）

教师出示统计表，指名说说和前面复式统计表的不同之处。

提出思考：在我们还没有进行数据收集的时候，哪个数据可以确定先填写？

有违常规的一问！同样激起了大家的议论。很快学生又都恍然大悟了，自己班的总人数、全班男生总数、女生总数不都是现成的数据吗？

接着指示学生收集了几个数据：学习古筝、葫芦丝、笛子的男生数，学习葫芦丝、笛子、小提琴的女生数。

老师问：留白处的小提琴男生数和古筝女生数的数据，你们能知道吗？

大家纷纷表示：通过计算，能很快算出这两组人数。

老师又问：如果公布剩下的这两组学生人数，一定是这两个数据吗？会出现什么情况？说明什么？

看似铁板钉钉的事儿，怎么还有疑问？有的说“要小心老师有诈”，有的说“我们一定会见证奇迹的”，有的说“不一致说明前边统计有误，得重来”……学生愉快地交流着，思维空前活跃。

巩固练习环节，教师灵活处理学习资料，引导学生逆向思考总数到部分数的数据处理方法。本班“学生总数”是一个客观已知条件，以此来带动整个数据链，使学生数学思维更加灵活。最后两个数据的验证，将统计和生活密切结合，客观理性地展示了统计的现实意义，是趣味性和现实性的有机结合。

六探：突破瓶颈源

本课时教学基于学生的旧知，通过观察引导学生发现单式统计表的相同点，进而进行整合和创造，在不断地探问中激活思维、闪现灵光，消除惰性等消极的学习行为，让思考走向深刻，让学习成为一种乐趣。

“复式统计图”是大家都比较熟悉的教学内容。那么，传统教学内容是否满足于习惯性教法还是力图嘗试更有效的教学探索呢？我想教师应该在教后反思的基础上增加一项本领，叫作“教后反刍”。

不论是教学内容还是教学对象，我们都得有“反刍”本领：看似熟知，尚需斟酌和推敲;初尝味浅，反复吐纳才显深味。如此，我们就能突破制约职业发展的“瓶颈”，教研才会越研越精彩，教师的创造之路也必定越走越明朗。也正因如此，教学的有效性也会越来越真实可信。

编辑 冯志强