基于FPGA+DSP的北斗信号快速捕获算法设计与实现

高唱 陈则王 曾庆喜 吕查德

摘 要： 为了解决北斗卫星接收机中传统并行频率捕获算法傅里叶变换需要处理的数据量大而影响卫星信号捕获速度的问题，提出了一种基于相干降采样的北斗信号快速捕获算法。利用FPGA+DSP（高速数字信号处理器+现场可编程逻辑门阵列），在传统的并行频率捕获算法中加入相干降采样模块，当信号进行载波剥离和伪码剥离后，通过降低采样频率的方式减小傅里叶变换需要处理的数据量，再对卫星信号进行三维搜索。结果表明，理论上所提算法计算量减少了80%以上，对实际北斗信号进行捕获时，平均每颗星的捕获时间为9.95 ms，内存资源消耗相比于传统并行频率捕获算法减少了42%。因此，新算法能在节约资源的同时有效提高捕获速度，可为进一步提高软件接收机的捕获性能提供参考。

关键词： 测试计量仪器;北斗;快速捕获;相干降采样;现场可编程逻辑门阵列（FPGA）;数字信号处理器（DSP）

中图分类号：TN967.1文献标识码： A

doi：10.7535/hbkd.2020yx06001

Design and implementation of BeiDou signal fast

acquisition algorithm based on FPGA+DSP

GAO Chang， CHEN Zewang， ZENG Qingxi， LYU Chade

（College of Automation Engineering， Nanjing University of Aeronautics and Astronautics， Nanjing， Jiangsu 211106，China）

In BeiDou satellite receiver， a fast BeiDou signal acquisition algorithm based on coherent down-sampling was proposed to solve the problem that the large amount of data to be processed by the Fourier transform affects the acquisition speed of satellite signals in the traditional parallel frequency acquisition algorithm. On the basis of FPGA+DSP （field-programmable gate arrays+digital signal processors）， the coherent down-sampling module was added to the traditional parallel frequency acquisition algorithm， and after the carrier and pseudo random code were stripped， the sampling frequency was reduced to decrease the number of points to be processed in the Fourier transform， and then a three-dimensional search for the satellite signal was performed. Theoretical analysis shows that the algorithm can reduce the amount of calculation by more than 80%; the experiments on the actual BeiDou signal indicate that the average acquisition time of each star is 9.95 ms， and the memory resource consumption is reduced by 42% compared with the traditional parallel frequency acquisition algorithm. This algorithm can effectively improve the acquisition speed while saving resources， which can provide reference for further improving the acquistition performance of the software receiver.

testing and measuring instruments; BeiDou; fast acquisition; coherent down-sampling; field-programmable gate arrays（FPGA）; digital signal processor（DSP）

北斗卫星导航系统（BDS）是中国研制的全球卫星导航系统，致力于为全球用户提供稳定可靠的卫星导航服务[1-3]。信号捕获是卫星接收机中的关键技术，用于搜索所有可见卫星并获得伪码相位和多普勒频移的粗略值[4-9]。卫星信号的捕获速度是评价接收机性能的重要指标。

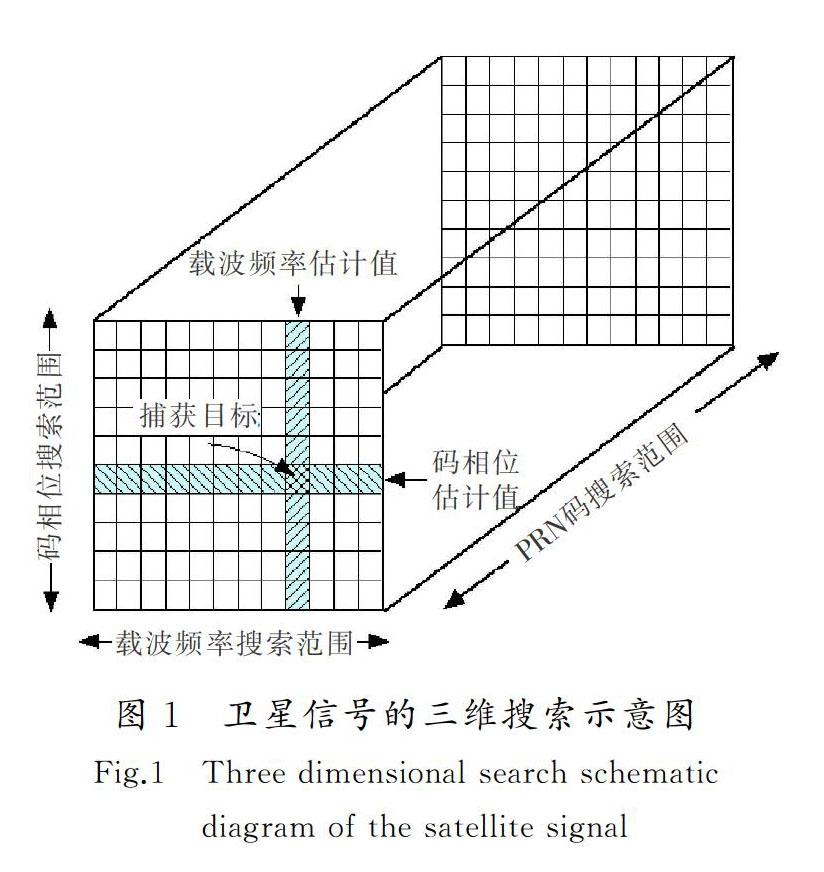
卫星信号的捕获就是对信号的三维搜索，即分别从PRN码、伪码相位和多普勒频移的方向进行搜索[10]。搜索过程如图1所示，每一小格的横向长度代表伪码相位搜索的步进值，一般取0.5个码片[11];每一小格的縱向长度代表载波频率搜索的步进值，一般取500 Hz。传统的串行捕获利用时域相关器在每一个PRN码上对信号的载波频率和码相位进行扫描式的二维搜索，其实现起来比较简单，且具有良好的捕获灵敏度，但是因为不同载波频率和码相位的组合很多，导致该方法的搜索范围大。此外，对于每一个码相位和多普勒频移的组合，其积分时间固定，捕获时间长[12]。

为了实现卫星信号的快速捕获，国内外学者提出了一系列基于频域的捕获算法。传统并行捕获算法有并行频率法和并行码相位法。并行频率法只需要对伪码相位进行遍历，减少了捕获时间，但是算法的并行性不够高，需要循环遍历的次数多，捕获效率低[13-15]。并行码相位法只对载波频率进行遍历，具有很好的并行性，但是其结构复杂，采样频率选择有限且在搜索每个载波频率点时需要进行2次傅里叶变换和1次傅里叶逆变换，运算量大，影响了卫星信号的捕获速度[16]。LIU等[17]提出了一种基于匹配滤波器和FFT（PMF-FFT）的捕获方法，利用伪码的自相关函数特性，在时域和频域2个维度同时对信号进行并行处理，该算法硬件实现简单，但是频率分辨率低。XIA等[18]提出了一种改进的PMF-FFT捕获方法，利用信号失锁前获得的多普勒频移值将捕获目标的范围缩小，并且用DFT代替FFT，解决了捕获精度与硬件复杂度之间的矛盾，实现了高动态卫星信号的捕获，但是相关输出峰值有较大的衰减。RAO等[19]利用信号在频域的稀疏特性，提出了基于稀疏傅里叶变换（SFT）的捕获方法，并分析了降采样因子对捕获速度的影响，该方法的计算复杂度随着参与运算信号长度的增加显著下降，但是SFT的实现较为复杂，且在降采样因子选取不合适时，结果误差较大。王凯等[20]提出了基于压缩感知改进的部分匹配滤波-快速傅里叶变换（CSPMF-FFT）算法，该算法减少了相关器的数目和FFT的运算量，节约了硬件资源，但是存在折叠噪声问题，影响了检测概率，而且在压缩比超过15时，重构概率会迅速降低到80%以下。

综上所述，现有的快速捕获算法都需要用到傅里叶变换且参与傅里叶变换的数据点数很多。针对这一问题，本文提出了加入相干降采样的并行频率捕获算法，在信号被剥离了码相位后先通过相干降采样模块再进行傅里叶变换。该算法降低了采样频率，使参与傅里叶变换的点数减少，减少了程序的运算量，节约资源的同时有效提高了捕获速度。

1 北斗信号结构

北斗信号采用码分多址（CDMA）方式，所有卫星发射具有相同载波频率的导航信号，通过伪随机码将共享相同载频的信号区分开。北斗信号是在载波上调制了伪随机码和导航电文的信号，调制方式为QPSK[21]。北斗B1信号是以下3种信号的组合：1）载波信号，频点在1 561.098 MHz的正弦信号，作为信号载体;2）伪随机码，有一定周期、取值为0和1的离散码序列，是识别卫星信号源自哪颗卫星的标识，同时也对初始信号进行了展宽。北斗B1信号的伪码速率为2.046 MHz，码长为2 046个码片;3）导航电文，包括星历信息、历书信息、卫星时钟相对系统时的修正参数和其他导航服务参数。北斗系统中加入了neumann-hoffman（NH）码对载波进行同步调制。北斗卫星的导航电文原始比特率为50 bit/s，经NH码调制后数据比特率变为1 000 bit/s。所以北斗B1信号的表达式为

sj（t）=AjB1CjB1（t）DjB1（t）exp[i（2π（fIF+fd）t+φj0）]，

式中：j为PRN码;AjB1为信号振幅;CjB1（t）为伪随机码;DjB1（t）为导航电文;fIF为载波频率;fd为多普勒频移;φj0为初始载波相位。

接收天线可以将卫星发射的电磁波信号转换为电压信号或电流信号，随后将信号送入射频前端进行处理。在经过射频前端模块中前置滤波器和前置放大器的处理后，信号变为频率较低、载噪比较高的中频信号，再经过A/D转换器的采样，得到的中频数字信号表达式为

sj（n）=AjB1CjB1（n）DjB1（n）exp[i（2π（fIF+fd）n+φj0）]+w（n），

式中：w（n）为双边功率谱密度是N0/2时的加性高斯白噪声。

2 基于相干降采样的快速捕获算法

2.1 算法原理

基于相干降采样的捕获算法实现框图如图2所示。其信号处理过程简述如下：第1步，将输入信号与本地载波信号相乘，实现数字下变频;第2步，信号和本地伪码信号相乘，完成伪码剥离;第3步，进行相干降采样，将采样后得到的信号进行离散傅里叶变换（DFT）;第4步，对DFT得到的结果取模，并对结果进行门限判决，若结果大于设定门限值，说明捕获成功。

对输入的中频信號进行载波剥离。将输入信号与本地载波相乘，从而使输入信号下变频到零中频信号。以某颗北斗卫星为例，只考虑其B1I分支信号，表达式为

s（n）=AC（n）D（n）exp[i（2π（fIF+fd）n+φ0）]+w（n），

式中：A为信号振幅;C（n）为C/A码;D（n）为导航电文比特;fIF为载波中频频率;fd为多普勒频移;φ0为初始载波相位;w（n）为白噪声分量，表示为

w（n）=wI（n）+iwQ（n），

其中wI（n）和wQ（n）分别代表在I支路和Q支路上均值为零且互不相关的正态噪声，它们的信号功率为σ2n。

输入数字中频信号经过和本地载波相乘的复下变频操作后，得到零中频数字信号，其表达式为

s0（n）=s（n）exp[-i（2πfIF）n]=AC（n）D（n）exp[i（2πfdn+φ0）]+w（n）。

对零中频数字信号进行剥离伪码的操作，其结果为

s1（n）=s0（n）C（n-m）=AR（m）D（n）exp[i（2πfdn+φ0）]+w（n），

式中：R（m）=C（n）C（n-m），其中m为本地伪码的码相位。北斗B1信号码长为2 046个码片，m=0，1，…，2 045。在信号捕获过程中，可以通过改变本地伪码的m值使本地伪码与捕获信号的伪码对齐。当本地伪码与捕获信号的伪码相位对齐时，即m=0时，有

R（m）=R（0）=1。

对完成载波剥离和伪码剥离后的信号进行采样频率为fS的相干降采样，即相当于对离散信号s1（n）的每M个点取1个平均值得到采样后的离散信号x（k），其表达式为

x（k）=1M∑M（k+1）n=Mks1（n）=1MTS∫MTS（k+1）MTSk

s1（t）dt=[DW]Asin（πfdMTS）MπfdTS

exp[i（2πfdMTSk+πfdMTS+φ）]+w（k），

式中TS为采样周期，TS=1/fS。

在相干降采样的过程中，I，Q支路的噪声特性没有发生变化，但是其平均功率变为

σ2wI=σ2wQ=12 σ2nM 。

通过DFT对信号进行频谱分析，首先对无限长信号序列进行加窗处理，将信号与矩形窗函数相乘，得到

x′（k）=x（k）rect（MTSL）=

AR（m）sin（πfdMTS）MπfdTSexp[i（2πfdt+πfdMTS+φ）]·

∑+∞k=-∞δ（t-MTSk）rect（tMTSL）。

将时域信号x′（k）转换为频域信号X（f），表示为

X（f）=AR（m）sin（πfdMTS）MπfdTS·[12πδ（2πf-2πfd）]·

[2πMTS∑+∞k=-∞δ（2πf-k2πMTS）]·[MTSLsinc（MTSLf）]=

AR（m）Lsinc（MTSfd）·[δ（2πf-2πfd）]·

[∑+∞k=-∞δ（2πf-k2πMTS）]·sinc（MTSLf）。

对无限长的频域信号X（f）进行离散加窗，得到

y（k）=X（f）∑∞k=-∞δ（f-kΔf）rect（MTSf）=

X（f）∑1/（2MTS）k=-1/（2MTS）δ（f-kΔf）。

在DFT过程中，噪声平均功率下降为σ2，其表达式为

σ2=σ2yI（k）=σ2yQ（k）=12

σ2nML 。

对DFT结果取模，得到

Y（k）=|y（k）|=yI（k）L 2+

yQ（k）L 2 。

Y（k）屬于莱斯分布，根据其概率密度分布曲线fn（z），由虚警率Pfa唯一确定捕获门限Vt，表示为

Pfa=∫+∞Vtfn（z）dz=

∫∞Vtzσ2e-z22σ2dz=

e-V2t2σ2，

Vt=σ-2ln Pfa 。

Y（k）的噪声分布属于瑞利分布，根据其概率密度分布曲线fs（z）和设定好的门限值Vt，可以求出信号的检测概率为

Pd=∫+∞Vtfs（z）dz。

2.2 算法性能分析

为了分析本文提出的捕获算法的性能，将传统并行频率捕获算法作为比较对象[22]。设置多普勒频移的搜索范围为[-10 kHz，10 kHz]，伪码相位的搜索范围为2 046个码片。若以500 Hz的频率步进值和1码片的码相位步进值进行捕获，则可以计算得到传统并行频率算法和L点降采样并行频率算法捕获过程所需要的计算量。以N点的采样深度计算，得到2种算法的运算量如表1所示。

由表1计算可知，取4 096点数据作64点DFT运算时，即N=4 096， L=64时，基于相干降采样的并行频率捕获算法比传统的并行频率捕获算法在乘法计算量和加法计算量上都减少了80%以上。

对北斗B1信号进行5 000次蒙特卡洛实验，以虚警率为横轴、检测概率为纵轴绘制受试者工作特征曲线（ROC曲线），分别采用传统并行频率捕获算法、L=64点相干降采样捕获法和L=32点降采样捕获法进行测试，得到曲线如图3所示。由图3可知，与传统并行频率捕获算法相比，加入相干降采样模块后的捕获算法检测概率有所降低。这是因为加入相干降采样模块后，得到的相关峰值结果低于传统并行频率捕获算法的峰值结果。当虚警率为0.1时，基于相干降采样的捕获算法相比传统并行频率捕获算法其检测概率仅下降0.1%。因此，本文提出的改进的并行频率捕获算法具有较好的捕获性能。

3 算法的FPGA+DSP实现

3.1 FPGA+DSP实现框架

由于基于FPGA+DSP的信号处理系统具有良好的并行处理能力，可以满足北斗B1信号快速捕获对实时性的要求，所以选择采用FPGA+DSP实现北斗B1信号的捕获。

基于FPGA+DSP的设计如图4所示。从天线进来的信号经过射频前端和低噪声放大后进入A/D通道，采样得到数字信号后送入FPGA内进行捕获，FPGA记录每一通道的捕获结果并给DSP发送捕获完成标志位。DSP通过地址总线和数据总线从FPGA中读取数据，对各通道的捕获结果进行门限判决。捕获系统采用12通道并行处理方式，每个通道的捕获实现分为载波剥离、伪码剥离、峰值检测和门限判决4部分。

3.2 载波剥离

通过本地载波信号和输入数字中频信号相关实现载波剥离。图5为载波剥离部分的实现框图，其中U1为载波NCO模块，U2为数字下变频模块。载波NCO模块的输入为和中频数字信号中心频率相对应的频率控制字，产生2路频率可调节的正交信号cos_I和sin_Q。数字下变频模块用于完成对输入信号载波的剥离，利用本地载波产生的2路相互正交的信号与输入的2路正交的采样信号相乘，将原有的数字中频复信号的载波剥离，只剩下基带调制的零中频数字信号。

3.3 伪码剥离部分

通过本地伪码与零中频信号相关实现伪码剥离，在信号被剥离伪码后通过相干降采样的方式对信号进行采样，对采样结果进行DFT。图6为伪码剥离部分的实现框图，其中：U3为DCM模块;U4为本地伪码产生模块;U5为相干降采样模块;U6为DFT实现模块。

DCM模块产生各个模块的工作时钟。本地伪码产生模块根据当前通道捕获的目标PRN码生成相应的伪码序列，然后根据码相位的搜索码片位置调整输出的伪码相位。实时采集2 ms的采样数据进行捕获处理，则有4 092个点进入相干降采样模块，首先将4 092点补零至4 096点，然后取M=64对信号进行降采样，将得到的降采样结果输入DFT模块。DFT模块在主时钟的驱动下，每获得1点降采样数据便对其进行1次64点DFT，当做完64点DFT时，即可获得完整的64点DFT结果。

通过FPGA片上debug工具SignalTap观察波形，结果如图7所示。图中Start_Acq为DSP控制的捕获开始标志位;ena_accum为相干降采样累加使能标志位，控制64点累加;Clear_Flg为清零标志位，控制累加结果清零;FFT_Valid_Flg为DFT完成标志位，为1时说明已经完成4 096点的处理，可以进行峰值检测。

3.4 峰值检测部分

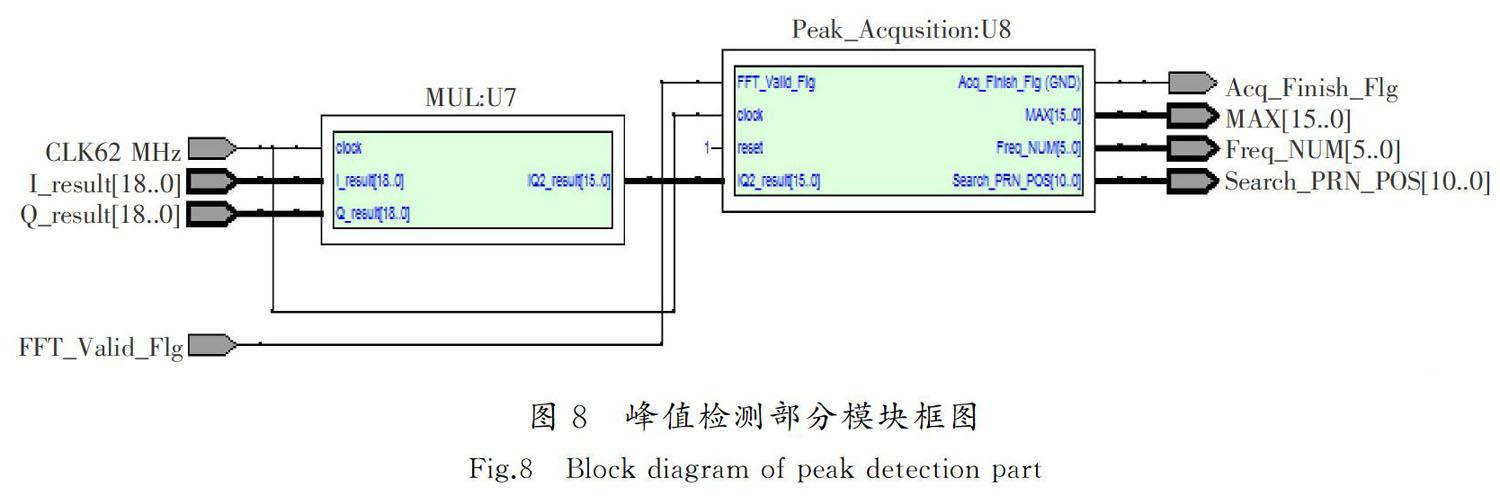
峰值检测部分负责遍历DFT峰值结果，得到捕获检测值。取码相位搜索步进值为1个码片，载波频率搜索步进值为500 Hz，循环搜索所有的伪码相位和载波频率，则可以得到每个搜索点对应的峰值能量。遍历得到的所有峰值，将DFT峰值结果中的最大值作为捕获判决的检测值，并记录检测值对应的载波频率和伪码相位。在捕获完成后，生成捕获完成标志位Acq_Finish_Flg发送给DSP。图8为峰值检测部分的实现框图，其中：U7为乘法器模块，负责计算DFT的峰值能量;U8为峰值检测模块，负责遍历DFT峰值能量并记录其最大值作为捕获检测值。

3.5 门限判决部分

DSP读取捕获完成标志位Acq_Finish_Flg为1时，对12通道的捕获结果进行门限判决，若检测值大于门限值，说明捕获成功，否则说明该通道没有捕获到该PRN码的卫星。之后，DSP重新分配新的目标PRN码给FPGA的12个通道，将捕获开始标志位Start_Acq置1，触发下一轮的捕获。

3.6 实验结果与分析

算法验证采用定制的GPSL1+BD2B1双模卫星导航开发平台，实物图如图9所示。接收机基带处理FPGA采用ALTERA公司的高性能芯片StratixII EP2S90F1020I4，DSP采用TI公司的高速浮点型处理器TMS320C6713。通过SignalTap截取一段对某颗北斗B1信号成功捕获的数据如图10所示。图10中，Acq_Finish_Flg为捕获完成标志，MAX为峰值结果，Freq_NUM为多普勒频移，Search_PRN_POS为码片位置。

表2为卫星接收机采用快速捕获算法2019-03-27T11：23在南京航空航天大学自动化学院的楼顶对北斗B1信号的捕获结果。在CCS3.3环境下，使用断点 和Profile测试100次捕获时间， 每次捕获平均消耗时间为119.36 ms，由于捕获模块集成了12个通道并行捕获，所以平均每颗星的捕获时间为9.95 ms。通过Quartus II软件查看片内存储资源占用情况，本文提出的算法占用的内存资源为12%，相比于传统的并行频率捕获算法减少了42%。

实验结果表明，基于相干降采样的并行频率捕获算法能夠实现对北斗B1信号的快速捕获，且捕获性能稳定，消耗的内存资源更小。

4 结 语

本文提出了一种新的捕获算法，在传统的并行频率捕获算法中加入相干降采样模块， 通过理论分析说明了该算法的计算量比传统并行频率捕获算法计算量减少了80%以上，并通过FPGA+DSP验证了算法的可行性，平均捕获每颗星的时间为9.95 ms，与传统并行频率捕获算法相比， 该算法的内存资源消耗减少了42%，可以实现北斗信号的快速捕获。

本文虽然只讨论了一个北斗B1信号的情况，但只需要调整本地振荡器的频率、采样点数和相干积分时间等相关参数，所提出的算法和硬件实现框架就可以适用于其他卫星信号，包括GPS，Galileo，GLONASS和其他GNSS信号。

尽管本文通过引入相干降采样的方式提高了捕获速度，但是并没有提高卫星信号的捕获精度。接下来的研究将针对高动态和高灵敏度的卫星信号进行研究，以期进一步提高软件接收机的捕获性能，让软件接收机快速捕获算法能够真正应用于工程领域。

参考文献/References：

[1]刘瑞华， 董立尧， 翟显. 北斗卫星导航系统空间信号用户测距误差计算方法研究[J]. 中国空间科学技术， 2017， 37（4）：41-48.

LIU Ruihua， DONG Liyao， ZHAI Xian. Research on calculation method of signal in space user range error for BeiDou Navigation Satellite System[J]. Chinese Space Science and Technology， 2017， 37（4）：41-48.

[2]BHUIYAN M Z H， SDERHOLM S， THOMBRE S， et al. Overcoming the challenges of BeiDou receiver implementation[J]. Sensors， 2014， 14（11）：22082-22098.

[3]王博， 焦海松， 谷庆，等. 北斗接收机动态定位精度测试与分析[J]. 导航定位学报， 2014， 2（2）：109-112.

WANG Bo， JIAO Haisong， GU Qing， et al. Dynamic accuracy testing and analysis for BeiDou receiver[J]. Journal of Navigation and Positioning， 2014， 2（2）：109-112.

[4]HU Zhiming， ZHANG Bo， LU Jinjian. FPGA implementation of stepping correlation acquisition algorithm for BeiDou II B1 signal[C]//2019 6th International Conference on Dependable Systems and Their Applications （DSA）.[S.l.]：[s.n.]，2020. doi：10.1109/DSA.2019.00049.

[5]LI Rongbing， HAN Zhifeng， LIU Jianye， et al. A high-sensitivity acquisition algorithm for BeiDou signals with NH code[J]. Journal of Navigation， 2019， 72（6）：1-15.

[6]RAKIPI A， KAMO B， CAKAJ S， et al. GPS signal acquisition and sensitivity analysis using different algorithms on a software receiver[C]//International Conference on Computational Intelligence. Riga： IEEE， 2015： 97-102.

[7]AZEEM U， AYUSH K D. Noise analysis on auto correlation of GPS coarse acquisition code[C]//International Conference on Communication & Network Technologies. [S.l.]：IEEE， 2015： 178-181.

[8]ZHU Can， FAN Xiangning. A novel method to extend coherent integration for weak GPS signal acquisition[J]. IEEE Communications Letters， 2015， 19（8）：1343-1346.

[9]AHAMED S F， LAVETI G， GOSWAMI R， et al. Fast acquisition of GPS signal using Radix-2 and Radix-4 FFT algorithms[C]//IEEE International Conference on Advanced Computing. [S.l.]： IEEE， 2016： 674-678.

[10]TANG Yinyin， GUO Xiye， WANG Yueke， et al. High-sensitive acquisition of signals for inter-satellite links of navigation constellation[J]. Electronics Letters， 2015， 51（23）：1879-1880.

[11]王爾申， 张晴， 雷虹，等. GPS空间信号可用性评估算法[J]. 电光与控制， 2017，24（2）：39-42.

WANG Ershen， ZHANG Qing， LEI Hong， et al. Evaluation algorithm of GPS signal in space availability[J]. Electronics Optics and Control， 2017（2）： 39-42.

[12]LECLERE J， CYRIL B， LANDRY R J， et al. FFT splitting for improved FPGA-based acquisition of GNSS signals[J]. International Journal of Navigation and Observation， 2015（2）：1-12.

[13]LEIBOVICH P E， JUAN G D， JAVIER G G， et al. Dedicated hardware for FFT based fast acquisition of GNSS signals[C]//2015 IEEE 6th Latin American Symposium on Circuits & Systems （LASCAS）. [S.l.]： IEEE， 2015.doi： 10.1109/LASCAS.2015.7250424.

[14]KIM B， KONG S H. Design of FFT-based TDCC for GNSS acquisition[J]. IEEE Transactions on Wireless Communications， 2014， 13（5）：2798-2808.

[15]ZHANG Yanbin， LYU Weijun， YU Dunshan. A fast acquisition algorithm based on FFT for BOC modulated signals[C]//TENCON 2015-2015 IEEE Region 10 Conference. [S.l.]： IEEE， 2016. doi： 10.1109/TENCON.2015.7372893.

[16]SOGHOYAN A， SULEIMAN A， AKOPIAN D. A development and testing instrumentation for GPS software defined radio with fast FPGA prototyping support[J]. IEEE Transactions on Instrumentation and Measurement， 2014， 63（8）：2001-2012.

[17]LIU Chang， ZHANG Jun， ZHU Yanbo， et al. Analysis and optimization of PMF-FFT acquisition algorithm for high-dynamic GPS signal[C]//IEEE International Conference on Cybernetics & Intelligent Systems. [S.l.]： IEEE， 2011. doi： 10.1109/ICCIS.2011.6070325.

[18]XIA Xuan， ZHAO Jiankang， LONG Haihui， et al. Fractional Fourier transform-based unassisted tracking method for global navigation satellite system signal carrier with high dynamics[J]. IET Radar， Sonar and Navigation， 2016， 10（3）：506-515.

[19]RAO M V G， RATNAM D V. Faster acquisition technique for software-defined GPS receivers[J]. Defence Science Journal， 2015， 65（1）：5-11.

[20]王凯，吴斌，汪勃.一种利用压缩感知改进的PMF-FFT扩频捕获算法[J].电讯技术，2018，58（6）：661-667.

WANG Kai，WU Bin，WANG Bo.An improved PMF-FFT spread spectrum signal acquisition algorithm based on compressed sensing[J].Telecommunication Engineering，2018，58（6）：661-667.

[21]China Satellite Navigation Office. BeiDou Navigation Satellite Signal in Space Interface Control Document Open Service Signal Version 2.1 [M]. Beijing： China Standardization， 2016.

[22]魯郁. 北斗/GPS双模软件接收机原理与实现技术[M]. 北京：电子工业出版社，2016.