基于GMM逆效应压力传感器的结构设计与研究

崔路飞 王传礼 喻曹丰 熊美俊

摘  要： 从传统压力传感器结构和超磁致伸缩材料逆效应原理入手，通过对闭合磁路和偏置磁场的研究，设计出一种新型的超磁致伸缩压力传感器，通过结构内部的霍尔传感器测量磁通量实现静态力的测量。利用Comsol软件进行有限元仿真，重点研究闭合磁路对磁通量的影响以及偏置磁场对传感器输出特性的影响规律。仿真结果表明：当采用闭合磁路装置时，能够对磁通进行引导，几乎没有漏磁通现象;存在一个最佳偏置电流（偏置磁场）使得传感器的灵敏度最高，求得灵敏度为0.44 mV/N。这为后面超磁致伸缩逆效应压力传感器的深入研究提供了一种技术途径。

关键词： 超磁致伸缩逆效应; 闭合磁路; 偏置磁场; 超磁致伸缩压力传感器; 有限元仿真; 灵敏度

中图分类号： TN602?34; TN03                     文献标识码： A                     文章编号： 1004?373X（2020）23?0164?03

Abstract： On the basis of the structure of traditional pressure sensor and the principle of inverse effect of GMM （giant magnetostrictive material）， a new type of giant magnetostrictive pressure sensor is designed by studying the closed magnetic circuit and bias magnetic field. The static force can be measured by measuring the magnetic flux with Hall sensor inside the designed sensor. The finite element simulation is carried out by Comsol software， and the influence of closed magnetic circuit on magnetic flux and the influence of bias magnetic field on the output characteristics of the sensor are studied. The simulation results show that， when the closed magnetic circuit device is used， the magnetic flux can be guided and there is almost no leakage magnetic flux; the presence of an optimum bias current （bias magnetic field） maximizes the sensor′s sensitivity， which is 0.44 mV/N. It provides a technical approach for the further study of giant magnetostrictive inverse effect pressure sensor.

Keywords： giant magnetostrictive inverse effect; closed magnetic circuit; bias magnetic field; giant magnetostrictive pressure sensor; finite element simulation; sensitivity

0  引  言

超磁致伸缩材料具有能量转化率高，尤其在电磁和机械能可逆转化之间[1?2]，凭借响应速度快、应变大、低频响应好、频带宽等特点被誉为21世纪高科技战略资源材料[3?5]。其中，超磁致伸缩逆效应是超磁致伸缩材料一个非常重要的特性，即对GMM施加外力時，GMM周围的磁通量会发生变化，这种现象被称为维拉里效应[6]。通过对磁通量的测量实现对力的测量，这对传感器来说具有极大的研究价值。虽然超磁致伸缩材料本身具有许多优点，但是超磁致伸缩传感器的研究尚处于起步阶段，对其报道较少。文献[7?8]设计了超磁致伸缩力传感器并进行了实验，验证了力传感器的可行性，但没有考虑内部漏磁现象。

本文在此基础上设计了超磁压力传感器结构，并对该传感器结构进行二维有限元仿真分析，得到闭合磁路装置能够对磁通进行引导，提高了传感器线性度和测量范围，这对用霍尔传感器测量磁通量的变化并转化为电压信号的输出来说，具有特殊意义。同时，得到了最佳偏置电流以提高传感器的灵敏度，这为后面超磁致伸缩逆效应力传感器的深入研究提供了一种方法与技术途径。

1  超磁致伸缩力传感器的基本原理与结构设计

超磁致伸缩力传感器的结构如图1所示。其结构分为三个部分，分别为闭合磁路装置、偏置磁场装置、测量装置。即外力直接作用在顶杆上，然后传递给导磁块，再传递给超磁致伸缩棒，超磁致伸缩棒在外力作用下其周围磁通量发生变化，最后用霍尔传感器测量磁通量。导磁块、上导磁体、圆筒磁轭、下导磁体形成闭合的磁路。目前，偏置磁场施加方式主要分为电流偏置式和永磁偏置式[9]。本文采用直流电流的激励线圈提供偏置磁场，以实现对偏置磁场的实时调节。用霍尔传感器检测磁通量的变化，其周围增加一个不锈钢钢环结构，以实现对超磁致伸缩力传感器灵敏度的提高。端盖与壳体通过内槽螺钉连接固定，对内部起到保护作用。

2.2  磁场仿真与分析

用Comsol软件对超磁致伸缩力传感器进行有限元仿真时，其端盖、壳体、预紧弹簧、内槽螺钉、预紧螺栓等结构影响特别小，可以忽略。

为了研究闭合磁路结构对磁通量的影响，在线圈中通入电流[I=]2 A的情况下，得到仿真结果如图2，图3所示。图2是没有闭合磁路结构仅有隔磁结构情况下的磁通量分布图，图3是有闭合磁路结构情况下的磁通量分布图。

通过图3与图2进行对比发现，只有隔磁结构并没有起到隔磁效果，而有闭合磁路结构的图3磁通密度分布合理，磁路完整，且磁通密度主要分布在磁路区域，闭合磁路几乎没有漏磁现象。这对用霍尔传感器测量磁通量并转化为电压的过程显然是合理的。

3  偏置磁场对传感器输出特性的影响

在传感器工作模式下，适当的偏置磁场使GMM棒刚好进入以磁畴偏转为主的阶段，导致传感器感知力的能力将增强[10]。为了确定偏置磁场对传感器输出特性的影响规律并确定最佳偏置磁场以提高传感器的灵敏度，对传感器在不同的偏置磁场下进行仿真。

3.1  偏置磁场有限元分析

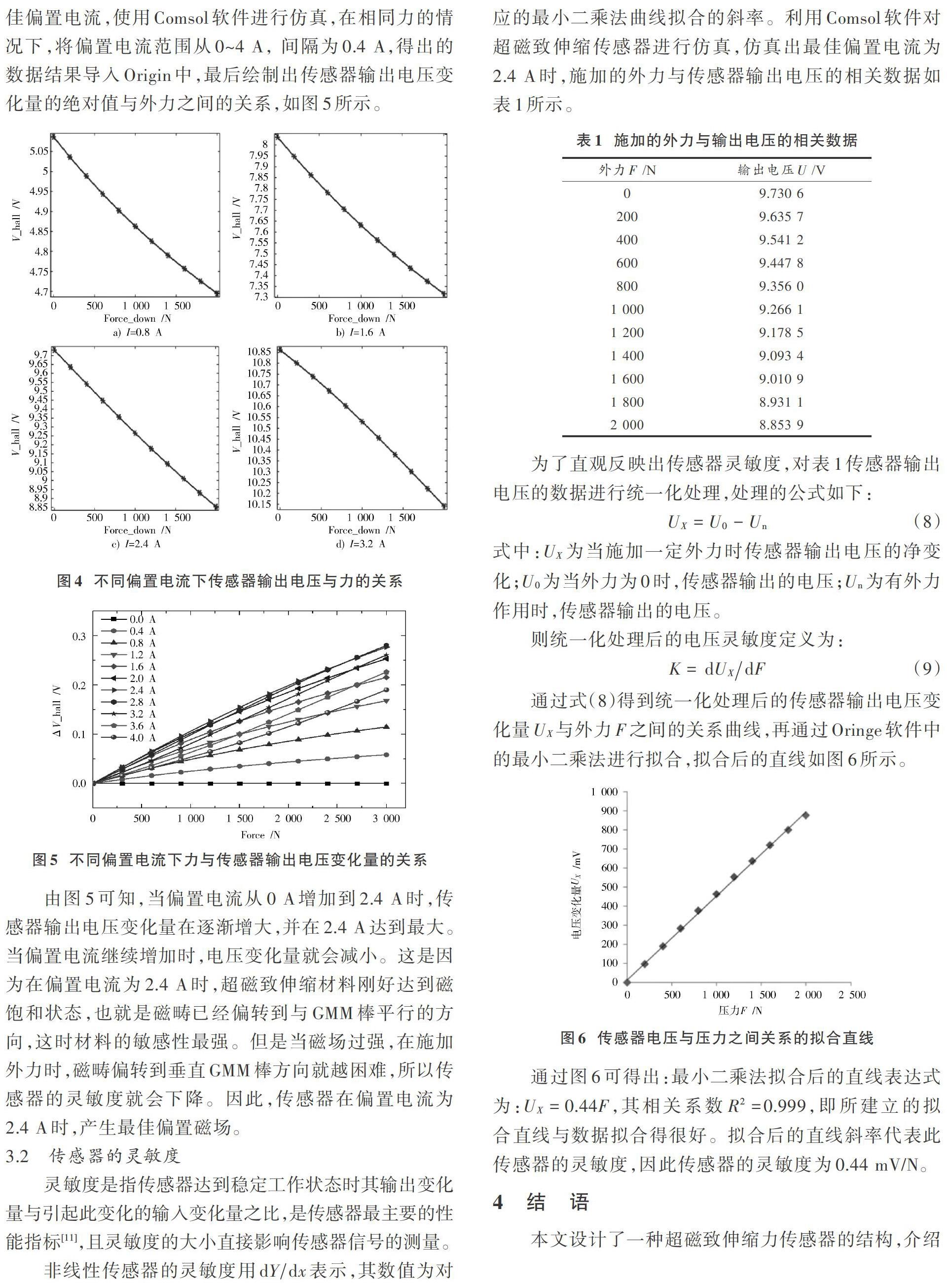
对偏置线圈施加不同的电流，其电流分别为0.8 A，1.6 A，2.4 A，3.2 A。用Comsol对其进行仿真，仿真出不同偏置电流下传感器输出电压与外力之间的关系，其结果如图4所示。

从图4中可以看出：外力在1 500 N以内线性关系较好，且随着外力不断增大，输出电压不断减小;当偏置电流不断增大时，输出电压也在不断增大。为了找出最佳偏置电流，使用Comsol软件进行仿真，在相同力的情况下，将偏置电流范围从0～4 A， 间隔为0.4 A，得出的数据结果导入Origin中，最后绘制出传感器输出电压变化量的绝对值与外力之间的关系，如图5所示。

由图5可知，当偏置电流从0 A增加到2.4 A时，传感器输出电压变化量在逐渐增大，并在2.4 A达到最大。当偏置电流继续增加时，电压变化量就会减小。这是因为在偏置电流为2.4 A时，超磁致伸缩材料刚好达到磁饱和状态，也就是磁畴已经偏转到与GMM棒平行的方向，这时材料的敏感性最强。但是当磁场过强，在施加外力时，磁畴偏转到垂直GMM棒方向就越困难，所以传感器的灵敏度就会下降。因此，传感器在偏置电流为2.4 A时，产生最佳偏置磁场。

3.2  传感器的灵敏度

灵敏度是指传感器达到稳定工作状态时其输出变化量与引起此变化的输入变化量之比，是传感器最主要的性能指标[11]，且灵敏度的大小直接影响传感器信号的测量。

非线性传感器的灵敏度用[dYdx]表示，其数值为对应的最小二乘法曲线拟合的斜率。利用Comsol软件对超磁致伸缩传感器进行仿真，仿真出最佳偏置电流为2.4 A时，施加的外力与传感器输出电压的相关数据如表1所示。

为了直观反映出传感器灵敏度，对表1传感器输出电压的数据进行统一化处理，处理的公式如下：

[UX=U0-Un] （8）

式中：[UX]为当施加一定外力时传感器输出电压的净变化;[U0]为当外力为0时，传感器输出的电压;[Un]为有外力作用时，传感器输出的电压。

则统一化处理后的电压灵敏度定义为：

[K=dUXdF] （9）

通过式（8）得到统一化处理后的传感器输出电压变化量[UX]与外力[F]之间的关系曲线，再通过Oringe软件中的最小二乘法进行拟合，拟合后的直线如图6所示。

通过图6可得出：最小二乘法拟合后的直线表达式为：[UX=0.44F]，其相关系数[R2=]0.999，即所建立的拟合直线与数据拟合得很好。拟合后的直线斜率代表此传感器的灵敏度，因此传感器的灵敏度为0.44 mV/N。

4  结  语

本文设计了一种超磁致伸缩力传感器的结构，介绍了其工作原理，并分析了磁通量的分布情况与偏置磁场对传感器输出特性的影响。然后通过仿真分析表明：

1） 闭合磁路结构使磁通密度分布合理且磁路完整，闭合磁路几乎没有漏磁现象，这对用霍尔传感器测量磁通量并转化为电压的过程显然是合理的。

2） 超磁致伸缩力传感器存在最佳的偏置磁场使传感器灵敏度最高，求得灵敏度为0.44 mV/N，且传感器的最佳偏置电流为2.4 A。

参考文献

[1] YANG Qingxin， YAN Rongge， FAN Changzai， et al. A magneto?mechanical strongly coupled model for giant magnetostrictive force sensor [J]. IEEE transactions on magnetics， 2007， 43（4）： 1437?1440.

[2] 钟长鸣.基于GMM薄膜声音传感器的发动机故障检测[D].淮南：安徽理工大学，2017.

[3] 喻曹丰，王传礼，邓海顺，等.超磁致伸缩驱动器磁场性能分析与优化[J].现代制造工程，2015（8）：136?140.

[4] 张慧.新型超磁致伸缩驱动器的设计及性能研究[D].上海：应用技术大学，2016.

[5] YADAV S， SHARMA P， YAMASANI P， et al. A prototype micro?thermoelectric power generator for micro?electromechanical systems [J]. Applied physics letters， 2014， 104（12）： 123903.

[6] 翁玲.超磁致伸缩振动传感器的模型与实验研究[D].天津：河北工业大学，2008.

[7] 攀长在，杨庆新，闫荣格，等.超磁致伸缩力传感器的模型研究[J].传感器与微系统，2007，26（3）：40?42.

[8] 刘慧芳，贾振元，王福吉，等.超磁致伸缩力传感器及其实验研究[J].大连理工大学学报，2011（6）：832?836.

[9] 谭先涛.超磁致伸缩驱动器的优化设计研究[D].上海：上海交通大学，2010.

[10] 唐志峰.超磁致伸缩执行器的基础理论与实验研究[D].杭州：浙江大学，2005.

[11] 王化祥.传感器原理与应用技术[M].北京：化学工业出版社，2017.