多特征加权指数熵在光斑中心定位中的应用
2020-12-23张明富马月辉段梦琨郑军飞孙晓贤
张明富 马月辉 段梦琨 郑军飞 孙晓贤

摘 要: 激光光斑中心检测是视觉测量中常用的关键技术,检测算法的优劣直接影响了测量的精度。针对现有光斑定位算法存在定位精度低、抗干扰能力差等问题,提出一种改进的激光光斑中心定位算法。该算法在Shannon熵的基础上引入指数熵,并根据光斑图像特征选取类内离散度最小和灰度对比度最大对指数熵进行加权处理,将使加权指数熵值最大时的灰度值作为阈值对光斑图像进行阈值分割,由此消除噪声干扰,最后由质心法进行光斑中心定位。实验表明,在兼顾稳定性的同时,与传统阈值分割方法相比,光斑中心定位误差降低了22%以上。
关键词: 视觉测量; 光斑定位; 指数熵应用; 阈值分割; 加权处理; 噪声干扰消除
中图分类号: TN911.73?34; TP391.41 文献标识码: A 文章编号: 1004?373X(2020)23?0020?04
Abstract: Detection of laser spot center is a key technology commonly used in vision measurement. The quality of detection algorithm affects the accuracy of measurement directly. In allusion to the problems of low positioning accuracy and poor anti?jamming ability of the existing spot location algorithms, an improved laser spot center positioning algorithm is proposed. The exponential entropy is introduced on the basis of Shannon′s entropy. According to the characteristics of the light?spot image, the exponential entropy is weighted by choosing the smallest intra?class dispersion and the largest gray contrast ratio. The gray value of the maximum weighted exponential entropy is used as the threshold to segment the spot image, and eliminate noise interference. The center positioning of the light?spot has been realized by the centroid method. The experiment results show that, in comparison with the traditional threshold segmentation method, the error of the laser spot center positioning algorithm is reduced by more than 22% while it gives consideration of stability.
Keywords: vision measurement; light?spot positioning; exponential entropy application; threshold segmentation; weighted processing; noise jamming elimination
0 引 言
基于视觉的形变测量系统具有精度高、非接触、受环境影响小等优点,在桥梁、隧道等重点监测场合应用广泛[1?2]。而大多数视觉测量系统选取亮度集中、抗传输介质干扰能力强的光斑作为待测物[3],因此快速准确的光斑定位是实现精确形变测量的前提。
常用的光斑定位算法有插值法[4]、二维高斯拟合法[5?6]、灰度质心法[7]以及多种改进算法。插值法通常以光斑最亮点作为插值中心,选取插值中心[x]轴和[y]轴4个节点进行插值计算。插值法计算量小、运算速度快,但计算精度极易受所选插值节点灰度波动影响。对于边缘含强干扰亮点的光斑图,插值中心易误选。二维高斯拟合法运算精度高,且稳定性好,对符合高斯分布的光斑图具有较好的鲁棒性。但其测量精度易受图像具体分布和采样数据样本大小影响,在实际应用中往往需要对图像和数据样本大小进行具体分析。灰度质心法对于均匀光斑能够精确定位,计算速度快,但抗噪能力差。直接光斑定位算法易受噪声影响,对此文献[8]采用先分割后定位处理光斑图像,结果证实对干扰抑制较好。文献[9]采用亮度阈值分割光斑图,后运用圆几何原理定位中心,算法简单且计算速度快。文献[10]对光斑图像去噪校正后采用OTSU法进行光斑分割,最后采用插值计算中心,检测结果稳定性优于对照算法。阈值法可有效消除噪声干扰,提高定位精度,但对光斑图进行阈值分割属于小目标分割,其目标背景比通常小于0.1,在此情况下,现有的分割算法易引入误差[11],进而影响光斑定位精度。
由以上原因,本文采用先阈值分割后进行光斑质心定位,且考虑到光斑与背景灰度值相差较大,准确分割后光斑内部灰度均匀,类内方差很小等特点,可用来弥补最大熵法只考虑目标背景最大平均信息量,却忽略图像灰度分布以及目标背景差异性。基于此,本文将图像灰度信息以及目标背景差异性作为权值对最大熵法进行加权处理,将加权指数作为光斑图像阈值选取准则对图像进行分割,以消除噪声干扰并减少计算量,然后通过质心法进行光斑定位,使定位结果兼顾实时性与高精度。
1 信息熵阈值选取
1.1 最大Shannon熵阈值选取
1.2 最大指数熵阈值选取
当图片灰度值[i]均存在,最大Shannon熵可快速准确选取最佳阈值。但对于光斑图像,其背景与目标相交处灰度突变较大,由此可造成特定灰度值比例较少甚至缺失。此時若[pi→0],则[ΔIpi→∞];若[pi=0],则[ΔIpi=log(1pi)]无定义。因此,本文引入一种改进的自信息量表示,使得事件获取的信息量满足以下原则[13]:
2 光斑定位算法的改进
2.1 方差加权指数熵
指数熵可获得更适合光斑特征的图像最大平均信息量,但却忽略了图像灰度分布的重要性,由于激光光斑量集中,在最优分割后,光斑内部灰度均匀,在数学上表现为类内方差很小,可根据该特征对光斑指数熵进行加权。在1.1节图像[i=fx,y]经阈值[T]分割后背景和目标平均灰度为[μ0]和[μ1]:
由于光斑灰度均匀,用其类内方差倒数对光斑信息熵进行加权,将使加权后的光斑信息熵远大于背景信息熵,为减少运算量,方差加权指数熵阈值选取公式可简化为:
2.2 多特征加权指数熵
将光斑类内方差作为权值计入其信息熵中,可以获得考虑目标灰度相关性的最佳分割阈值。但图像最小类内方差的计算依据是误差平方和最小,在该准则下当不同类别包含个体数相差较大时,将大类分割开可能使误差平方和更小。光斑图像属于小目标分割,其特征是目标背景之比通常小于0.1,将该准则应用于光斑最小类内方差选取,将背景划分为光斑的一部分可获得更小的类内方差,此时用类内方差对信息熵进行加权获得更大的方差加权信息熵,造成光斑错误分割进而影响定位精度。
对于具有一定信噪比的光斑图像,待检测的光斑部分平均灰度一般明显高于其背景平均灰度值,且灰度均值不受目标大小影响,基于此特性,为体现光斑与背景之间的灰度差异,引入光斑和背景平均灰度差作为权值来消除类内方差可能存在的误分割。背景和目标平均灰度分别为[μ0]和[μ1],考虑到目标背景所占比例,则式(11)方差加权指数熵可改进为:
3 光斑定位精度分析
3.1 高斯噪声影响下光斑定位精度
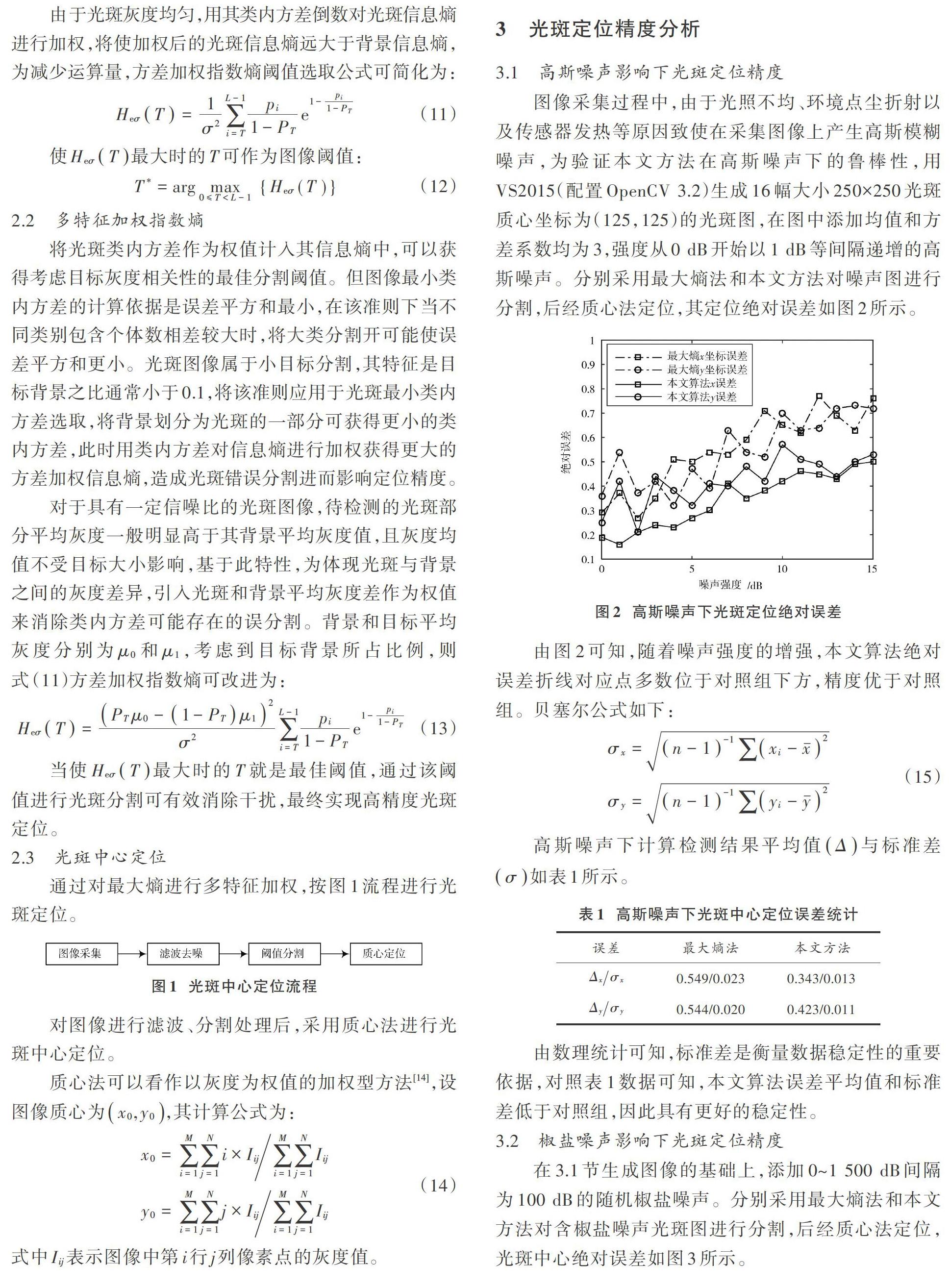
图像采集过程中,由于光照不均、环境点尘折射以及传感器发热等原因致使在采集图像上产生高斯模糊噪声,为验证本文方法在高斯噪声下的鲁棒性,用VS2015(配置OpenCV 3.2)生成16幅大小250×250光斑质心坐标为(125,125)的光斑图,在图中添加均值和方差系数均为3,强度从0 dB开始以1 dB等间隔递增的高斯噪声。分别采用最大熵法和本文方法对噪声图进行分割,后经质心法定位,其定位绝对误差如图2所示。
由数理统计可知,标准差是衡量数据稳定性的重要依据,对照表1数据可知,本文算法误差平均值和标准差低于对照组,因此具有更好的稳定性。
3.2 椒盐噪声影响下光斑定位精度
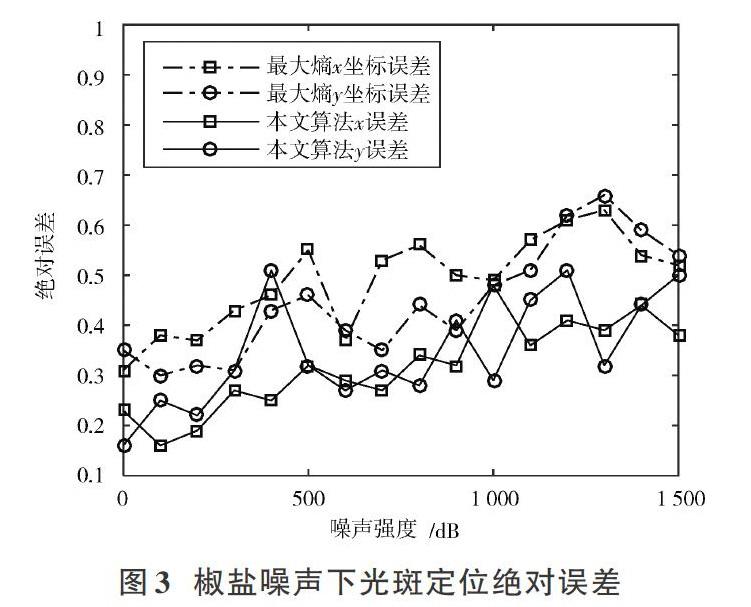
在3.1节生成图像的基础上,添加0~1 500 dB间隔为100 dB的随机椒盐噪声。分别采用最大熵法和本文方法对含椒盐噪声光斑图进行分割,后经质心法定位,光斑中心绝对误差如图3所示。
椒盐噪声下计算检测结果平均值[Δ]与标准差[σ]如表2所示。
由表2数据可知:本文算法标准差小于对照组,具有更好的稳定性。对比平均误差,本文算法误差在[x]方向降低了35%,在[y]方向上降低了22%,在兼顾鲁棒性的同时,提高了定位精度。
4 结 语
光斑中心检测广泛应用于视觉测量中,是视觉测量的关键技术,其定位精度直接决定了相关设备应用效果。本文将光斑灰度分布以及图像目标背景灰度差异作为权值,对最大熵法进行加权,并将加权最大熵作为图像阈值的分割准则,弥补了现有最大熵法对图像灰度分布以及目标背景差异性利用不足等问题,提高了光斑定位精度。实验结果表明,与对照组相比,本文算法抗干扰能力强,兼具稳定性与高精度。
参考文献
[1] 刘兆蓉,王志乾,刘绍锦,等.激光光斑中心精确定位算法研究[J].计算机仿真,2011,28(5):399?401.
[2] DONG Hongjun, WANG Long. Non?iterative spot center location algorithm based on Gaussian for fish?eye imaging laser warning system [J]. Optik?International journal for light and electron optics, 2012, 123(23): 2148?2153.
[3] XU Yongfeng. A photogrammetry?based experimental modal analysis method by tracking visible laser spots [EB/OL]. [2019?08?20]. https://www.researchgate.net/profile/Yongfeng_Xu.
[4] 张秋佳,赵玉华.基于加权插值算法的激光光斑中心检测[J].激光与红外,2016,46(1):81?84.
[5] 陈和,杨志浩,郭磐,等.激光光斑中心高精度定位算法研究[J].北京理工大学学报,2016,36(2):181?185.
[6] 郭晴晴,张运杰,李新,等.星载激光高度计地面光斑质心定位方法研究[J].量子电子学报,2018,35(3):338?343.
[7] 席剑辉,包辉.基于改进质心法的激光条纹中心提取算法[J].火力与指挥控制,2019,44(5):149?153.
[8] 徐亚明,束进芳,安动动.自适应阈值激光光斑中心定位方法研究[J].城市勘测,2014(4):5?7.
[9] 郭玉静,魏丽.一种基于亮度阈值的激光光斑中心定位算法[J].测试技术学报,2017,31(3):223?226.
[10] 张绍堂,吴鸿,宁德琼.一种高精度的激光图像光斑中心检测方法[J].激光杂志,2018,39(8):153?156.
[11] 吴一全,吴加明,占必超.一种可有效分割小目标图像的阈值选取方法[J].兵工学报,2011,32(4):469?475.
[12] 吴一全,殷骏,毕硕本.最大倒数熵/倒数灰度熵多阈值选取[J].信号处理,2013,29(2):143?151.
[13] 葛启承,林锦国,肖迪.基于信息熵的图像阈值选取算法[J].江苏科技大学学报(自然科学版),2010,24(5):485?488.
[14] 李朋,高立民,吴易明,等.加权质心法亚像元定位误差研究[J].电子测量技术,2011,34(6):43?46.
