一类三维非线性系统的复杂簇发振荡行为及其机理1)

马新东 姜文安 张晓芳 韩修静 毕勤胜

∗(江苏大学土木工程与力学学院,江苏镇江 212013)

†(江苏科技大学船舶与海洋工程学院,江苏镇江 212003)

引言

多尺度效应广泛存在于自然界的各种实际系统中,如不同神经细胞的簇放电行为[1-3]、飞机的高速旋转与慢速平动的耦合[4]、化学系统中的同质液相催化反应[5]和周期激励扰动下齿轮振荡器的快慢行为[6]等.多尺度的耦合往往使系统表现出大幅振动和小幅振动的组合[7],这种现象被称为簇发振荡[8-10].大幅振动通常对应着系统在大振幅极限环内的运动,小幅振动对应着系统在平衡点或小振幅极限环内的运动.连接大幅振动和小幅振动的可以是分岔[11-12],也可以是其他形式的动力学行为,如脉冲式爆炸(PSE)[13-14]和吸引子的快速逃逸(speed escape of attractor)[15]等.

一般说来,多尺度效应可以分成三类:第一种是时域上的,即系统各状态变量之间存在变化速率上的显著差异,数学方程中出现小参数扰动(0 < ε ≪1);第二种是频域上的,即系统中存在不同量级的频率耦合,数学方程中出现与系统自然频率有着量级差异的周期激励频率(0 < ω周期≪ω自然);第三种是时域和频域的耦合,由于快慢分析方法的限制,这类系统的研究存在较大的困难,目前只有较少的文献[16-18].但这几篇文献也仅仅研究了激励频率远大于小参数的情况.对于前两类多尺度效应,人们进行了深入研究,取得了丰富的成果.如在时域多尺度方面,古华光[19]利用实验和理论相结合的方法,揭示了外激、参激和噪声等不同调控机制下神经元的多种簇放电模式及其转迁规律;樊登贵等[20]从基于基底神经节−丘脑皮层电路的帕金森神经元网络出发,给出了电荷平衡双相脉冲−深部脑刺激的最优控制,并进行了生理实验验证;包伯成等[21]提出了一种具有快慢结构的三维Morris-Lecar 神经元模型,通过分岔图、时间序列等分析了混沌簇发和周期簇发等的机理; Desroches等[22]研究了由尖峰加周期分岔引起的簇发振荡现象,在这种动力学行为中鸭式解起到了核心作用.

在频域多尺度方面,郑健康等[23]研究了参数激励下一类三维混沌电路系统由叉形分岔滞后诱发的不同簇发行为及其机理; 韩青爽等[24]利用分岔图、时间历程图等分析了周期激励下水轮机调速系统高温气动薄膜的簇发特性;Zhou 等[25]分析了两个参数激励下最小化学反应系统的簇发,给出了4 种基于跨临界分岔滞后的新型簇发形式;Makouo 和Woafo[26]在数值方面分析了两种激励下van der Pol 振荡器的周期和混沌簇发现象,并进行了实验验证;Kovacic 和Lenci[27]研究了低角激励频率下纯非线性振子的簇发,这种振动模式是由绕慢流形的快速振荡组成.

自激系统是自然界中广泛存在一类动力系统,它的振荡由系统自身的运动维持,如薄壁可缩软管的自激振荡现象[28],轮轨摩擦自激振荡引起的钢轨波磨现象[29],热声发动机的起振[30]和激波串的自激振荡[31]等.如果自激系统某些参数发生周期变化且周期变化频率远小于系统固有频率时,系统会出现簇发振荡等丰富的动力学行为.如Zdzislaw[32]研究了圆盘式单极发电机通过一个小振幅正弦电压发生器向直流电动机供电时的簇发振荡、混沌振荡等的产生条件.Shaw 等[33]对辉光放电等离子体自激装置中的“fold/fold cycle” 型混沌簇发和混沌尖峰振荡等进行了实验研究.Wang 和Ma[34]给出了噪声影响下简化光学参量振荡器的簇发振荡产生机理.时培明等[35]分析了一类含准周期参激刚度和摩擦阻尼的非线性扭振系统的周期簇发现象及其动力学转迁.尽管对于自激系统不同形式的簇发及其机理研究已经得到了丰富的成果,但由于多尺度效应的复杂性,使得这类系统的动力学特性仍需要进一步研究.本文针对一类自激单圆盘单机发电机三维非线性动力系统[36-37],研究了系统在参数激励作用下的不同簇发行为,如图1 所示.该三维非线性系统可以描述两种自激同极发电机系统的动力学行为,这两种发动机系统在数学上是等效的,都含有法拉第圆盘和线圈,不同的是一个含电容器,另一个含与线圈串联的电机.系统的数学模型如下

其中,x表示系统的重标电流,y表示圆盘的角转动速度,z表示电容器的电荷或电机的角速度.α 表示力偶,κ 表示机械摩擦,β−1表示测量电枢的转动惯量或电容,ρ 表示电动机的机械摩擦或漏泄电阻.这里将参数β 用函数β0+β1cos ωt调制,其中激励频率ω 满足0 < ω1.这样ω 与系统固有频率ω0之间出现了量级差异,系统(1)成为一个典型的两时间尺度自激系统,其中方程(1)是快子系统,方程=−ωβ1sin ωt是慢子系统.该系统动力学行为的研究可以作为类似非线性低维系统研究的基础,可以用于描述地球物理流体动力学中某些有趣的现象.诸如地球液态金属核中自激磁流体动力发电机作用产生的主要地磁场和地球大气−海洋系统的“厄尔尼诺−南方涛动”等,它们的动力学行为会表现出类似于非线性弛豫振荡(或簇发振荡)的特性,这是由大气和海洋之间复杂的尺度效应相互作用的结果.

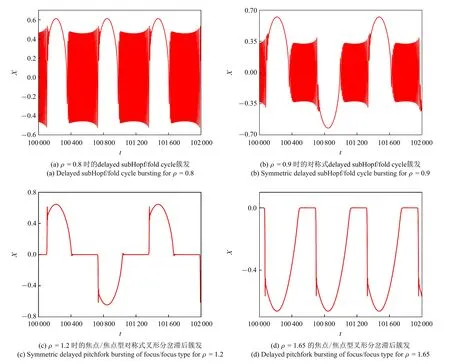
图1 参数β0=1,β1=0.8,α=2,κ=1,ω=0.01 时的不同簇发行为Fig.1 Different patterns of bursting oscillations for β0=1,β1=0.8,α=2,κ=1 and ω=0.01

本文以三维非线性电机系统(1)为例,围绕多时间尺度簇发振荡问题,旨在揭示亚临界Hopf 分岔滞后和叉形分岔滞后行为诱发的多种簇发振荡现象机理,以及典型参数对簇发动力学的影响.本文的组织结构如下:在第1 节中,研究了快子系统的稳定性和分岔,给出了Hopf 分岔、叉形分岔等典型分岔的产生机制.利用(β,x)平面内的相图与分岔图的叠加,第2 节分析了对称式亚临界Hopf 分岔滞后簇发产生机理.第3 节给出了对称式亚临界Hopf 分岔滞后簇发随参数ρ 变化的动力学转迁,得到了亚临界Hopf 分岔滞后簇发、焦点/焦点型对称式叉形分岔滞后簇发和焦点/焦点型叉形分岔滞后簇发3 种不同簇发模式.最后,第4 节总结全文.

1 系统的稳定性与分岔

对于方程(1),在任意参数条件下都会存在平衡点E0(0,α/κ,0).在E0处将系统线性化,可以得到Jacobian 矩阵

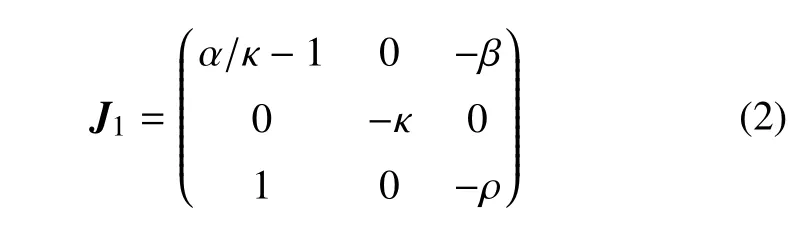
E0的稳定性由对应的特征方程F(λ)=a0λ3+a1λ2+a2λ +a3决定,其中a0=1,a1=κ+ρ+1 −α/κ,a2=κρ+(κ+ρ)(1 −α/κ)+β,a3=κρ(1 −α/κ)+βκ.当参数满足a0a3−a1a2> 0 且a1> 0,a3> 0 时,E0是稳定的.当a1a2−a0a3=0 时,特征方程出现一对纯虚根,此时系统出现Hopf 分岔,产生振荡频率为=κρ+(κ+ρ)(1 −α/κ)+β 的极限环.

为了更清晰地说明系统的分岔行为,固定参数ρ=0.9,其他参数取值与图1 相同,对应的系统稳定性和分岔特性如图2 所示.从中可以得到如下结论:平衡点E0总是不稳定的;当β>βLPC=0.807 1 时,此时的稳定吸引子为极限环LC1;当β 随时间慢变穿越叉形分岔点PB,出现另外两个平衡点E1,2,并且在区间0.823 3=βsubH<β<βPB=0.9 内,E1,2都是不稳定的;E1,2的稳定性可以通过亚临界Hopf 分岔subH1和subH2 改变,同时产生两个不稳定的极限环LC2 和LC3,通过matcont[38]数值模拟可知LC2 和LC3 的振荡幅值会逐渐增大.当β 变化到达极限环的fold 分岔点LPC 和同宿分岔点Homo(βLPC=βHomo=0.807 1)时,LC2 和LC3 与LC1 和不稳定平衡点E0碰撞消失.然后,在LPC 的左侧只有两个稳定的平衡点E1,2.

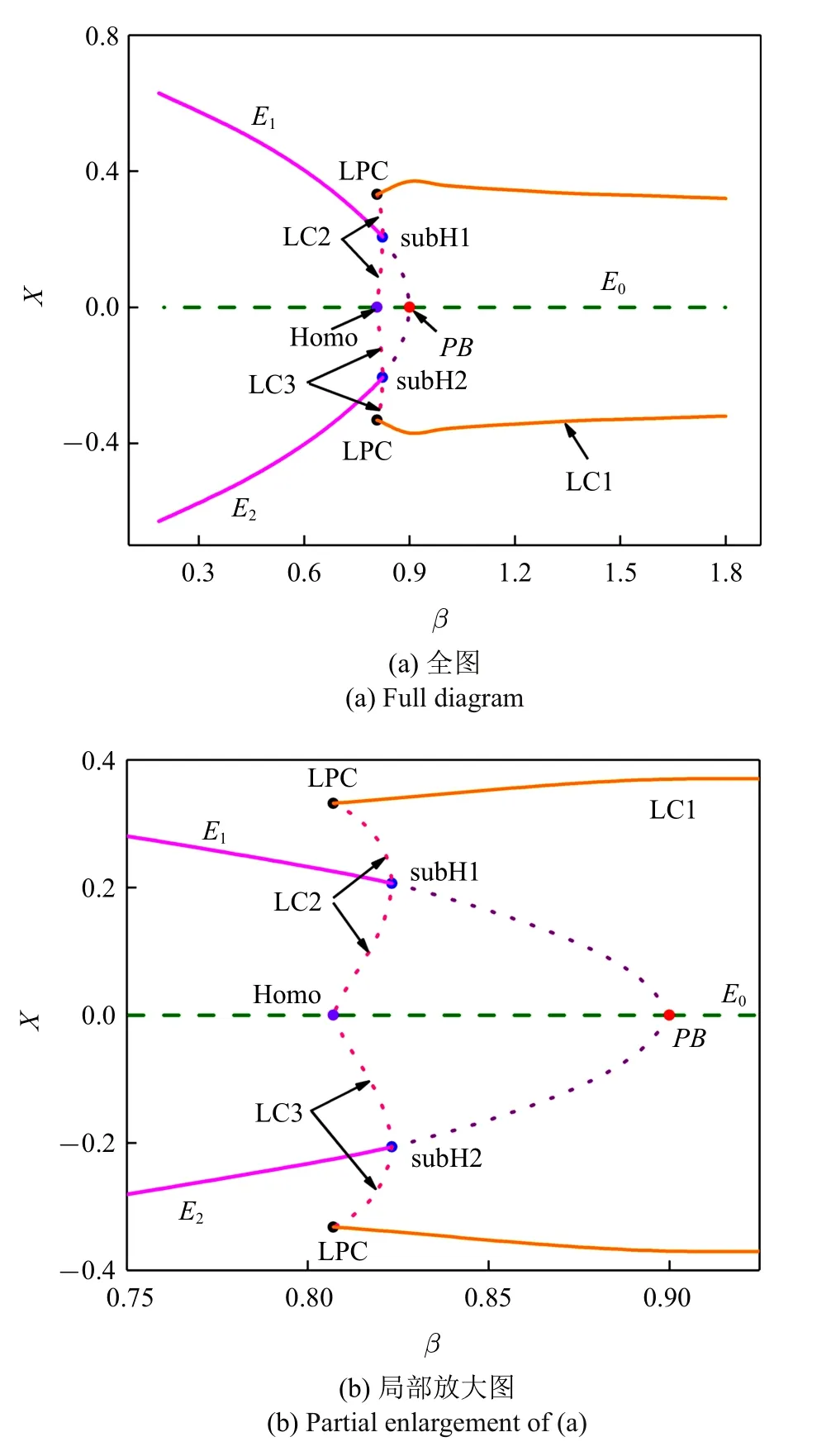
图2 ρ=0.9 的单参数分岔图Fig.2 One-parameter bifurcation diagram for ρ=0.9

2 对称式delayed subHopf/fold cycle 簇发

上节以ρ=0.9 为例研究了系统的稳定性和分岔条件,基于此,这部分揭示ρ=0.9 时的动力学行为机理,其他参数的取值与图1 相同.图3 给出了ρ=0.9的系统相图和时间序列,可以发现,这种快慢动力学行为显然与稳定极限环和稳定平衡点有关,这与图2的分析相符.

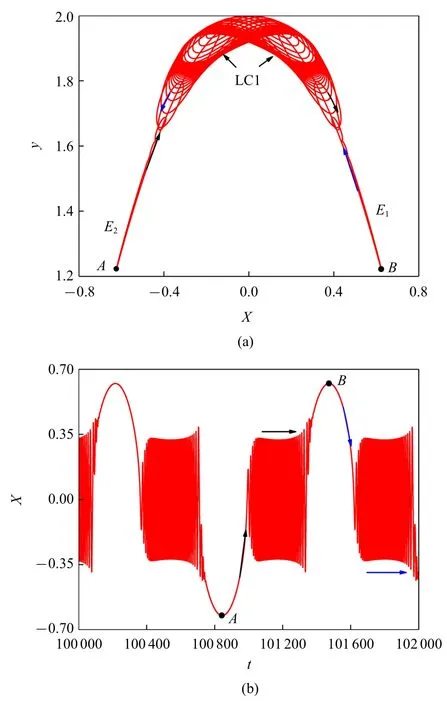
图3 ρ=0.9 的相图和时间序列图Fig.3 Phase diagram and time series for ρ=0.9

图4 ρ=0.9 时(β,x)平面上的相图与分岔图的叠加Fig.4 The superposition of the phase diagram in(β,x)plane and bifurcation diagram for ρ=0.9

这种快慢动力学行为的产生机制可以通过叠加(β,x)平面上的相图和分岔图[39]得到,见图4.假设轨迹从β 的最大值1.8 处开始运动,此时的稳定吸引子为极限环LC1,LC1 的向量场使轨迹在LC1 的最大振幅和最小振幅之间大幅运动.随着β 减小到βPB,叉形分岔使系统出现另外两个不稳定的平衡点E1,2.当β 穿越βsubH1和βsubH2后,E1,2通过亚临界Hopf 分岔稳定,同时产生两个不稳定的极限环.同时可以看到,在subH1 和subH2 附近极限环LC1 的振荡幅值变大,然后LC1 与两个不稳定极限环在极限环的fold分岔LPC 处碰撞消失,与此同时,两个不稳定的环也与不稳定平衡点E0曲线碰撞,出现同宿分岔Homo.最后,在LPC 和Homo 的左侧只剩下稳定的平衡点E1,2,轨迹经过短暂的振幅逐渐减小的高频振动后进入平缓的平衡点运动,直至β 减小到其最小值0.2.

当β 从0.2 逐渐增大过程中,E1,2在subH1 和subH2 处失稳,但小幅平衡点运动仍未消失,轨迹会继续沿着不稳定的E1,2运动一段时间,表现为参数穿越亚临界Hopf 分岔的慢通过效应,或者亚临界Hopf分岔滞后.经过一段滞后区间(见图4(b),滞后区间宽度约为0.14),轨迹进入稳定极限环LC1 中大幅振荡,直至β 增大到其最大值1.8,一个周期过程结束.

在这种快慢行为中,大幅运动开始于亚临界Hopf 分岔滞后,结束于极限环的fold 分岔,而且在一个周期内存在两个对称的大幅运动,因此这种簇发模式可以称为对称式delayed subHopf/fold cycle 簇发.

3 簇发的动力学转迁

上节给出了ρ=0.9 时的对称式亚临界Hopf 分岔滞后簇发的产生机理,下面研究这种簇发行为随参数ρ 变化的动力学转迁,其他参数的取值仍与图1相同.

3.1 两参数分岔图

图5 给出了系统关于参数β 和κ 的两参数分岔集,从中可以发现β 从最小值−4 到最大值4 存在两种穿越形式:一种是区域1,即这个过程只穿越了叉形分岔曲线PB;另一种是区域2,这个过程穿越了极限环的fold 分岔曲线LPC、亚临界Hopf 分岔曲线subH 和叉形分岔曲线PB.穿越形式的不同,会使系统出现不同的动力学行为.

对称式亚临界Hopf 分岔滞后簇发是区域2 中当LPC 曲线与subH 距离较远时的典型行为,ρ 的取值不会定性改变系统的动力学特性,因此可以取定参数ρ=0.9 进行研究.

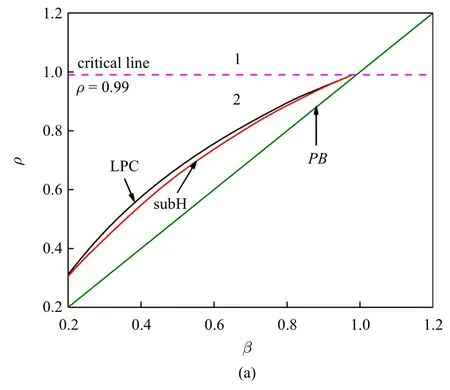
图5 系统关于β 和ρ 两参数分岔图Fig.5 Two-parameter diagram related to β and ρ

3.2 Delayed subHopf/fold cycle 簇发

当图5 区域2 中的LPC 曲线与subH 距离较远时,如ρ=0.8,由于LPC 分岔点和subH 分岔点距离很远,系统的动力学行为受初始点的影响很大.图6 给出了当初始点分别为(0.001,0.001,0.001) 和(−0.001,−0.001,−0.001) 时的相图和时间历程,可以发现这两部分关于x=0 是对称的.

这种簇发行为的产生机制如图7 所示.当轨迹从β 的最大值1.8 处开始运动时,此处的稳定吸引子为LC1,轨迹在LC1 中做大振幅振荡.当β 穿越叉形分岔PB 后,产生不稳定平衡点E1.E1的稳定性通过亚临界Hopf 分岔subH1 改变,同时产生一个不稳定极限环.当β 到达极限环的fold 分岔LPC 时,稳定极限环LC1 与不稳定极限环碰撞消失.然后轨迹沿着稳定平衡点E1曲线运动,直至β 的最小值0.2.在β增大过程中,E1通过亚临界Hopf 分岔失稳,轨迹继续沿着不稳定E1运动一段时间,表现出分岔滞后效应(此时滞后区间宽度约为0.16),随后进入稳定极限环LC1 中运动.

由图可见,大幅运动开始于亚临界Hopf 分岔滞后,结束于极限环的fold 分岔,因此这种快慢行为可以称为delayed subHopf/fold cycle 簇发.

3.3 焦点/焦点型对称式叉形分岔滞后簇发

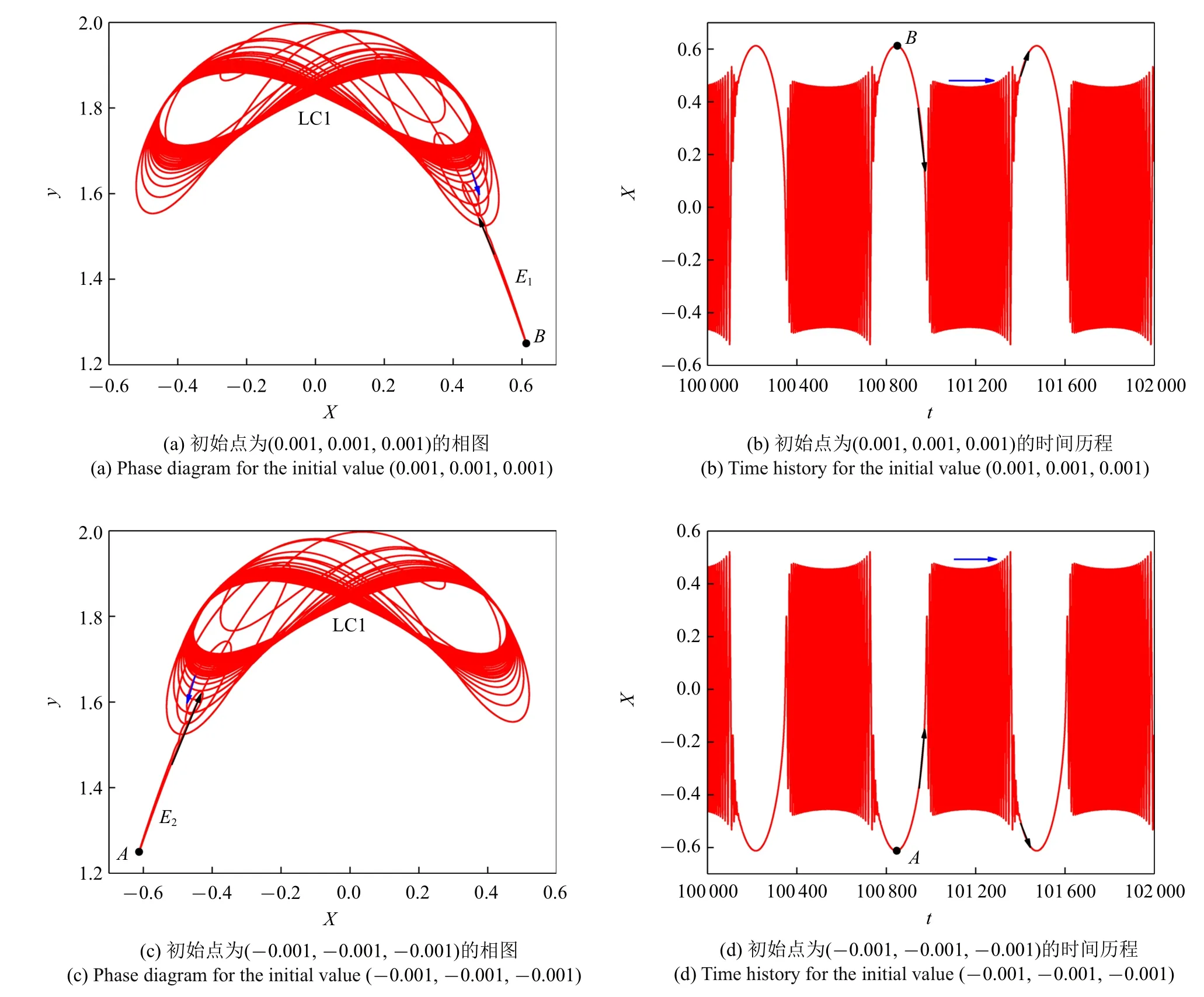
图6 ρ=0.8 的相图和时间历程图Fig.6 Phase diagram and time history for ρ=0.8

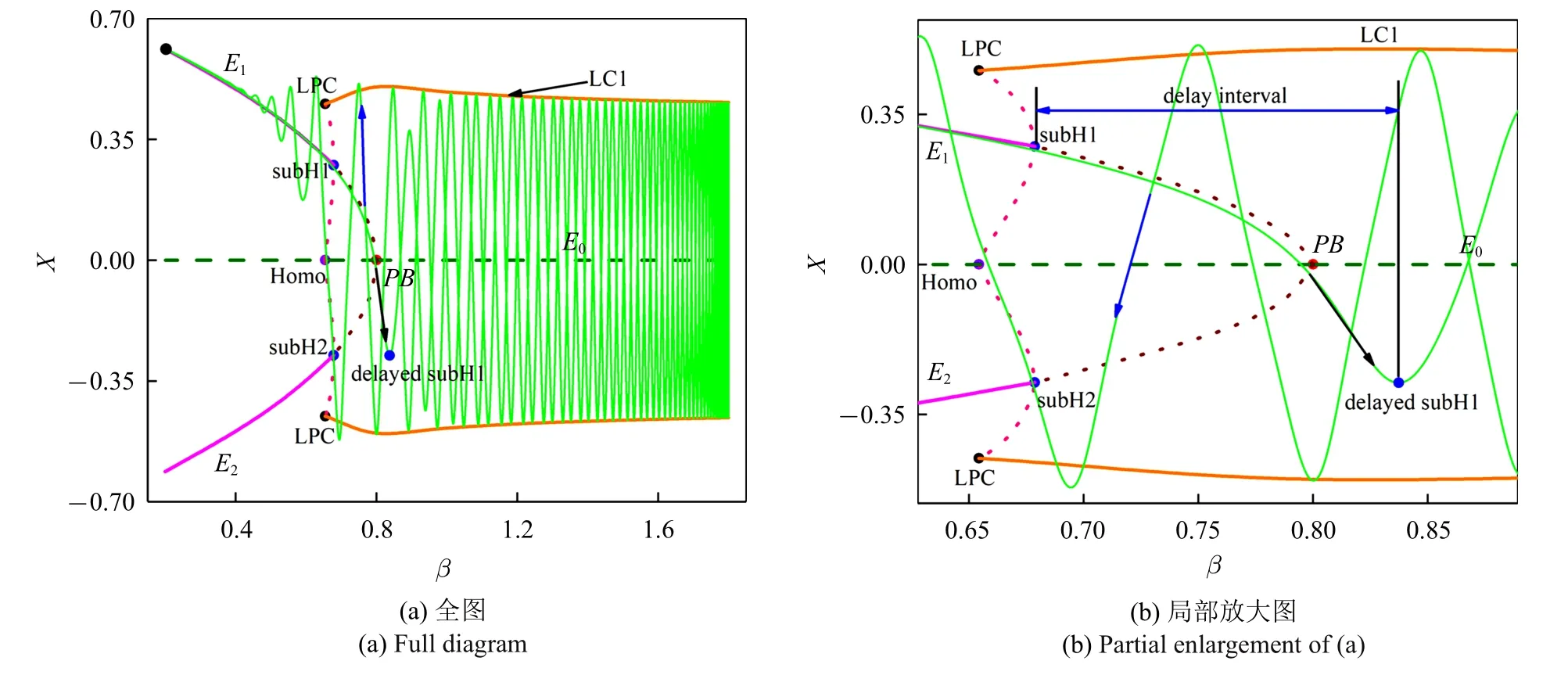
图7 ρ=0.8 时(β,x)平面上的相图与分岔图的叠加Fig.7 The superposition of the phase diagram in(β,x)plane and bifurcation diagram for ρ=0.8

当参数ρ 增大进入区域1 时,可以看到此时β双向变化只会穿越叉形分岔PB,表现为系统动力学在不同平衡点之间的转迁.因此,平衡点的类型会决定系统动力学的特性.如当ρ=1.2 时,E0是稳定的焦点(当β=1.52 时,特征方程的特征根为λ1=−1,λ2,3=−0.1 ± 0.557i),E1,2也是稳定的焦点(当β=0.906 时,特征方程的根为λ1=−1.08,λ2,3=−0.18 ± 0.714i).此时,系统的动力学行为只与焦点有关,对应的相图和时间序列如图8 所示.

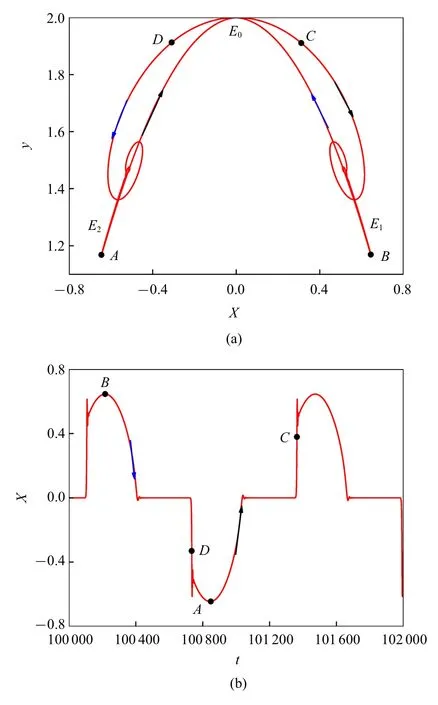
图8 ρ=1.2 的相图和时间序列Fig.8 Phase diagram and time series for ρ=1.2

图9 给出了ρ=1.2 时的快慢动力学分析.当β从1.8 逐渐减小时,轨迹会沿着稳定平衡点E0的平衡曲线做近似直线运动.随着β 穿越叉形分岔PB,系统出现了另外两个稳定平衡点E1,2.但在图9 中可以看到,由于叉形分岔滞后的原因,轨迹沿着不稳定的E0又运动很长一段时间才转到E1,2中运动,直到β到达其最小值0.2.然后β 又开始逐渐增大,轨迹从沿着E1,2平衡曲线运动经过叉形分岔转入到E0的平衡曲线运动,直至完成一个周期运动.

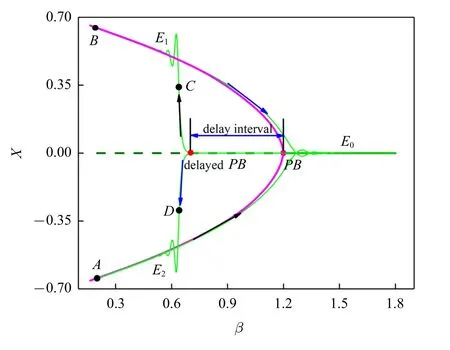
图9 ρ=1.2 的快慢动力学分析Fig.9 Fast-slow analysis for ρ=1.2

这种快慢动力学行为是轨迹从一个稳定焦点进入另一个稳定焦点的运动,而且存在上下两个对称结构,同时又可以看到明显的叉形分岔滞后特性(此时的滞后区间宽度约为0.5),因此这种簇发行为可称为焦点/焦点型对称式叉形分岔滞后簇发.

3.4 焦点/焦点型叉形分岔滞后簇发

随着ρ 的增大,对称结构发生破却,初始取值决定了系统轨迹离开E0平衡曲线后的走向.图10 给出了当ρ=1.65 时,初值分别为(0.001,0.001,0.001)和(−0.001,−0.001,−0.001)的相图和时间历程图.

从图11(a)可以看到系统轨迹从E0的平衡曲线进入E1的平衡曲线时,出现了一个很大的滞后区间.并且随着ρ 的增大,这种叉形滞后区间的宽度越来越小(图11(a)的滞后区间约为0.66,图11(b)的滞后区间约为0.32,图11(c)的滞后区间约为0.06,图11(d)的滞后区间为0).这种动力学仍是从焦点到焦点的簇发行为,并且没有存在对称结构,因此该簇发称为焦点/焦点型叉形分岔滞后簇发.

4 结论

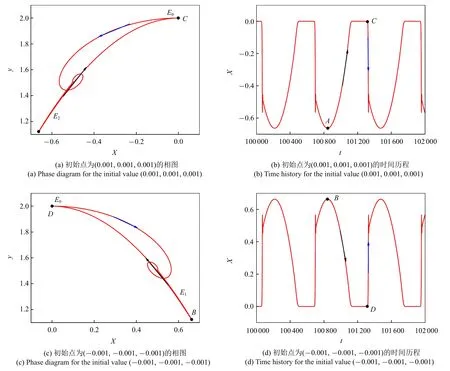
图10 ρ=1.65 的相图和时间序列Fig.10 Phase diagrams and time series for ρ=1.65

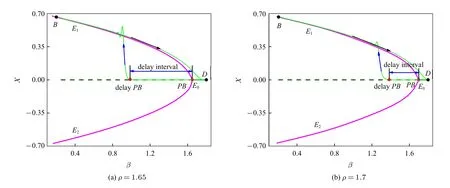
图11 (β,x)平面上的相图与分岔图的叠加Fig.11 Overlapping of the phase diagram in(β,x)plane and bifurcation diagram

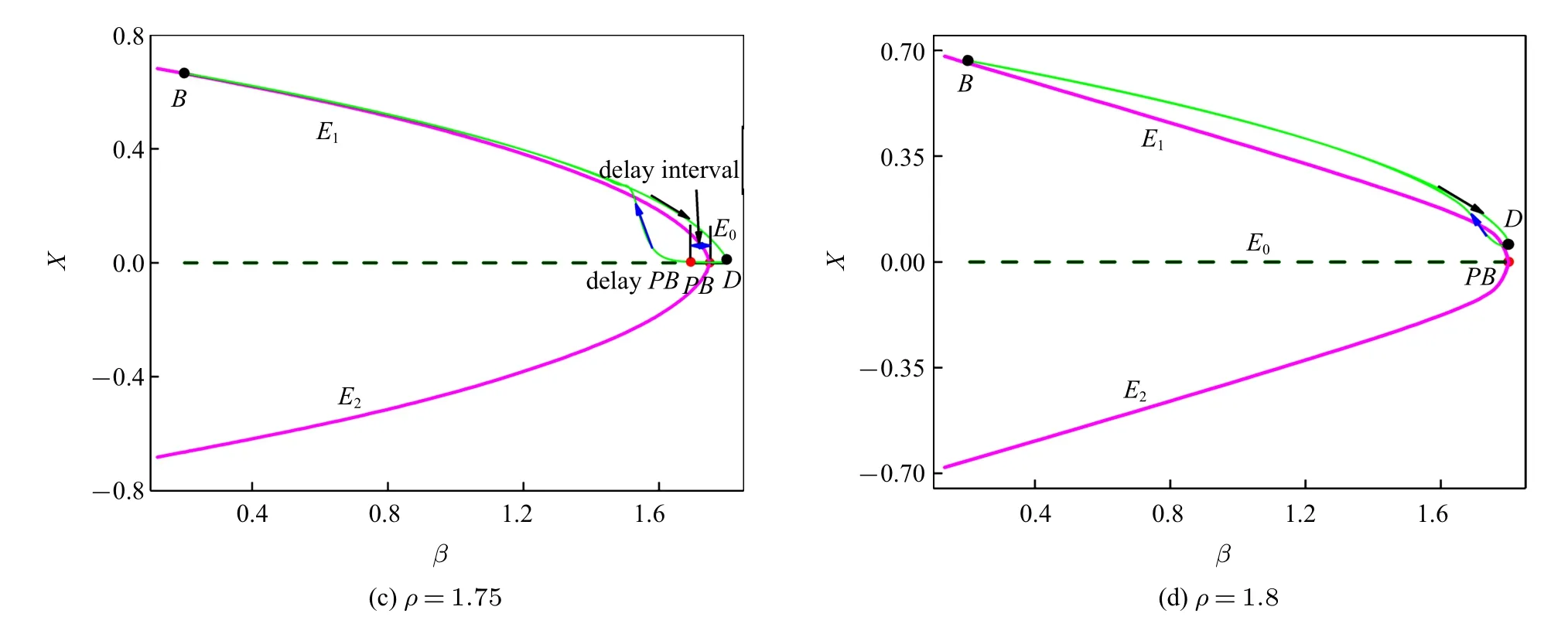
图11 (β,x)平面上的相图与分岔图的叠加(续)Fig.11 Overlapping of the phase diagram in(β,x)plane and bifurcation diagram(continued)

参数激励下的两时间尺度非线性系统可以产生非常复杂的簇发行为.在给定的参数条件下,对快子系统进行分岔分析,发现系统会出现叉形分岔、亚临界Hopf 分岔、极限环的fold 分岔和同宿分岔,此时系统对应的簇发形式为对称式亚临界Hopf 分岔滞后簇发.在这种簇发行为中,发现了明显的亚临界Hopf分岔滞后现象.然后,借助两参数分岔图,研究了对称式subHopf/fold cycle 簇发随参数ρ 变化的动力学转迁,得到了delayed subHopf/fold cycle 簇发、焦点/焦点型对称式叉形分岔滞后簇发和焦点/焦点型叉形分岔滞后簇发,这些簇发的产生与ρ 和初始点的选取有关.同时,随着ρ 的增大,亚临界Hopf 分岔滞后区间宽度逐渐减小,叉形分岔滞后区间宽度先增大后减小.