面内随机堆叠石墨烯复合材料压阻传感机理与压阻性能1)
2020-12-23李正杨庆生尚军军刘夏
李正 杨庆生 尚军军 刘夏
(北京工业大学力学系,北京 100124)
引言
面内随机堆叠石墨烯复合材料(graphene composites,GC)是由基底材料(例如聚合物)和随机堆叠于基底表面的石墨烯片构成的.因为由它制成的应变传感器具有良好的压阻效应和柔韧性,得到了人们的极大关注.许多基于GC 纤维[1-3]、薄膜[4-6]以及织物[7-8]的传感器件的研究工作已被报道,它们可以应用到医疗电子、环境监测和人工智能等领域,例如由其制造的智能电子皮肤既可以察觉肺的呼吸、心脏的跳动这样的小变形,也可以感知身体各关节的屈伸这样的大变形.石墨烯的制备方法、基底材料以及GC 的组装方法的差异使得它们的压阻性能有所不同.为了改进和革新生产技术、提高压阻性能,许多研究工作已经被开展.Son 等[9]在预拉伸的尼龙缠绕橡胶线(NCRYs)上喷涂石墨烯片制备的GC 感知范围可达310%,为减少外部环境对压阻性能的影响在NCRYs 表面增加了共聚酯保护层.Jia 等[10]通过在还原氧化石墨烯/热塑聚氨酯纤维表面粉刷聚多巴胺获得了多功能应变传感器,聚多巴胺的引入不仅使其具有很好的透气性还防止了还原氧化石墨烯从热塑聚氨酯表面脱落.Wei 等[11]采用水辅助转移法制备了一种激光还原氧化石墨烯聚乙烯醇薄膜复合材料,由其制成的传感器贴附于喉结能够让哑巴发声.Das 等[12]在不使用任何有害化学物质和复杂工艺的情况下,在生物兼容的尼龙膜上制备了高性能纸基表皮传感器,可以对人的心脏、大脑、肌肉以及运动进行监测.Fu 等[13]应用还原氧化石墨烯片涂装玻璃纤维/硅胶复合材料生产了柔性应变传感器,该传感器不但具有很好的灵敏度还可以对感知结构进行增强.然而,目前为了实现GC 的商业化,大部分研究工作集中在革新与改进制备方法上,对于压阻传感机理的研究由于观测技术的限制基本停留在通过实验现象与结果进行推理上.
为了建立复合材料的宏观性能与微观结构的联系,从更深层次研究复合材料的工作机理和性能,数值建模和数值模拟是经济有效的方法[14-16].尤其对于由石墨烯片随机堆叠而成的GC,优势更为突出.Wang 等[17]为研究由石墨烯与织物构成的石墨烯复合材料的压阻性能,基于改进的Voronoi 多晶微观模型建立了等效电阻网络,但该模型很难应用到多层石墨烯堆叠制成的复合材料.Hempel 等[18]由随机分布的等尺寸圆片的本身电阻与接触电阻建立了一张电子渗流网络,通过求解基尔霍夫方程组对其进行了研究.Tao 等[19]采用有限差分的方法求解欧姆定律微分方程计算了不同网格密度的复合材料的电阻应变曲线,但未考虑接触电阻的影响.当前虽然针对GC 的数值模拟开展了一些工作,但对于GC 的压阻传感机理仍然不是十分清楚,另外接触电阻对一些GC 压阻效应的产生起到至关重要的作用,如何在计算过程中体现接触电阻的贡献有待解决.
本文基于面内随机分布石墨烯复合材料的微结构特点,建立了一个新的二维GC 传感器模型,发展了压阻性能的计算方法,探讨了GC 的压阻传感机理和微结构参数对压阻性能的影响.
1 二维GC 传感器模型
根据石墨烯片在复合材料内随机堆叠分布的结构特征[20],在边长分别为l+2a和l,厚度为h的区域内随机投入边长为a,厚度为t的石墨烯方片构建GC 传感器模型.由于石墨烯片与复合材料薄膜的厚度远小于它们的另外两个尺度,假设石墨烯片相互贯穿且厚度与复合材料薄膜相同,如图1(a)所示,红线包络区域为电极(l×a×h),工作区(l×l×h)被电极与绿线包络,蓝线包络表示电极与工作区被聚合物封装.由于在该模型中长方体的厚度h等于石墨烯片的厚度t,因此它是一个准二维模型,于是由它简化得到的二维模型(图1(b))可用于研究GC 的压阻性能.在GC 传感器模型中每片石墨烯的中心坐标以及它与x方向的夹角分别由0 ∼1 间的3 组均匀分布随机数确定,例如,初始状态,第i片石墨烯中心坐标及石墨烯片与x方向的夹角分别为,,其中分别为3 组随机数中第i个元素.

图1 GC 传感器模型构造过程示意图Fig.1 Schematic of GC sensor model construction process
在本模型中进行如下假设:(1)由于石墨烯的面内刚度远大于聚合物基底的刚度,将石墨烯片视为刚性片.(2)因为石墨烯与聚合物之间存在较强的范德华力,基底能够将变形完全传递到石墨烯片,另外,随机堆叠的石墨烯片很难实现公度接触,而非公度接触石墨烯片具有超滑能力[21],所以GC 的变形可认为是均匀的,即石墨烯片中心相对于整个模型位置保持不变.若模型沿x方向伸长,第i片石墨烯任意时刻的中心坐标可表示为

其中ε 为GC 沿x方向的正应变,µ为基底材料的泊松比.
取橡胶作为基底材料,不可压缩材料橡胶的泊松比取0.5 仅适用于小变形条件,对于能够感知大变形的GC 不再适用.为计算橡胶的泊松比,在由橡胶制成的受力板内任选单元体如图2 所示,单元体的初始体积V0=dxdydz,在单向应力σx作用下,单元体变形后体积V1=(1+ε)(1 −µε)2dxdydz,作为不可压缩材料,橡胶在变形过程中体积不变,即

求解上式可得

因为1 −µε 恒大于0,上式只能取负号,橡胶的泊松比为
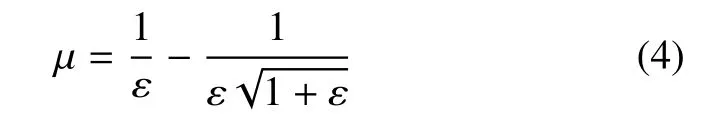

图2 橡胶板与其单元体Fig.2 Plate made of rubber and its volume element
由于石墨烯片随机堆叠,GC 传感器模型(图1(b))中有些独立存在的石墨烯片与导电网络没有联通,对电子迁移没有贡献.移出这部分石墨烯片,可以得到能够直接应用有限单元法计算的GC 传感器模型,如图1(c)所示.
2 电场计算有限元格式
为分析GC 传感器模型(图1(c))的电阻变化,在模型的两个电极上分别输入、输出恒定电流,电位φ的求解就是如下Laplace 方程的边值问题.
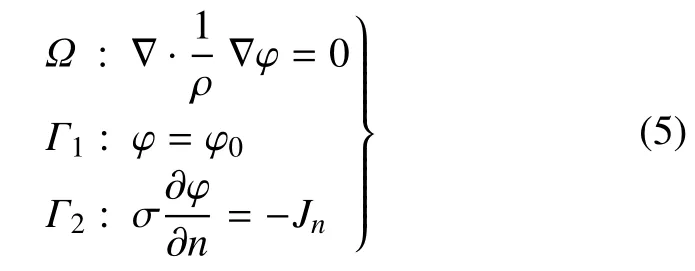
式中,ρ 为石墨烯的电阻率,φ0为边界上的电位,Jn为边界上输入电流的电流密度.应用式(5)可以建立恒流电场的有限元格式

上式也可表示为

3 GC 压阻传感机理
石墨烯复合材料的压阻效应源于在复合材料中的石墨烯片形态改变(搭接石墨烯片的相对滑移与分离以及石墨烯薄膜的断裂),石墨烯片间的接触电阻与隧道效应[22-23].
因为在间距为几个纳米的石墨烯片间存在隧道效应,所以电子可以在两片分离的石墨烯片间迁移,并且两片石墨烯间的电阻随着石墨烯片间距的增大指数式升高.这也是一些石墨烯复合材料具有压阻效应的重要原因.但是在GC 中,当电子可由石墨烯片的搭接实现迁移时,一些分离的石墨烯片由于隧道效应的存在,依然可以作为一个并联支路,该支路的电阻远大于其他支路的电阻,由并联电阻公式可以证实,这个支路对整个网络电阻的贡献很小,因为并联电路的总电阻取决于电阻小的支路;随着GC 的伸长,当某个位置石墨烯片分离后,电子不再能由石墨烯片的搭接实现迁移时,由串联电阻公式可知,在该位置由隧道效应产生的电阻将主导整个网络的电阻,但是隧道效应发挥作用的传感范围仅有几个纳米,对于能够感知大变形的GC,隧道效应对于GC 压阻性能的贡献不能被应用,所以本文不考虑隧道效应对GC 压阻性能的影响.
为了研究GC 中石墨烯片的形态对压阻性能的影响,研究认为石墨烯片与片之间完全接触即不考虑接触电阻的影响,选择橡胶作为基底材料,模型中石墨烯片的含量用面分比ω 表示

其中,m是模型中石墨烯的片数,A为每片石墨烯的面积,A0为模型的面积.将边长为5 µm 的方片以面分比为1.2 随机堆叠于工作区边长为100 µm 的GC 传感器模型中,由单层石墨烯的方阻与厚度分别为125 Ω/sq[24]和0.335 nm[25]可知它的面内电阻率ρ0=4.187 5×10−14TΩ·µm,因为多层石墨烯搭接区域的面内等效电阻等于各单层电阻的并联值,所以模型中搭接区域的面内电阻率可取为ρ0/n,其中n是石墨片堆叠的层数.
灵敏度系数β 是判断传感器压阻性能的一个重要指标,它表示单位应变的相对电阻,即

由上式可知,灵敏度系数为常数时,相对电阻随应变线性变化,反之,非线性变化.

图3 GC 相对电阻与灵敏度系数曲线Fig.3 Curves of GC relative resistance and gauge factor

表1 传感器模型的形态与电流密度云图Table 1 Configuration and current density contour of the model
图3 表明有些相对电阻线性增大、灵敏度系数近似为常数,有些相对电阻急剧变化、灵敏度系数不再稳定.为了解上述现象产生的原因,对20% < ε <30% 时模型的形态与电流密度云图(表1) 进行分析.当20% < ε < 25%时石墨烯片仅产生了滑移,电流密度云图中也只有石墨烯片的滑移导致的电子迁移路径长度的增长,可知图3 中相对电阻的线性增大与灵敏度系数恒定不变是由石墨烯片的滑移产生的;当25% < ε < 30%时大部分石墨烯片彼此滑移而只有一小部分发生了分离,由于石墨烯片的滑移仅能产生电子迁移路径长度的增长,所以电子迁移路径数量减少与无效片数量的增多是由石墨烯片的分离导致的,而此时相对电阻发生了突变,灵敏度系数不再为常数,所以石墨烯片的分离导致电子迁移路径数量的减少与无效片数的增多,使得相对电阻的非线性变化、灵敏度系数不稳定.无效片是指孤立于电子迁移网络的石墨烯片或仍然与电子迁移网络相连,因远离电子迁移通道,其上电流密度很低的石墨烯片.GC 实验得到的相对电阻应变曲线初始阶段线性增大,后期非线性增长的现象[8-10]可由上述结论合理解释,因为在GC 变形的初始阶段石墨烯片间的形态改变以滑移为主,后期才出现了分离.由上述分析可知,石墨烯片形态改变产生压阻效应的具体原因是石墨烯片的滑移导致的电子迁移路径长度的变化与分离导致的电子迁移路径数量和无效片数量的改变.
GC 传感器模型整个变形过程中的石墨烯形态与电流密度云图(表2)表明随着纵向伸长,在纵向石墨烯片彼此滑移,由于重叠面积减小,模型中高电阻率面积增大,低电阻率面积减小,伴随一些石墨烯片彼此分离,间距增大,甚至一些石墨烯片脱离电子迁移网络,导致电子迁移路径长度增长,电子迁移路径的数量减少,无效片数增多,这些因素均使整个电子迁移网络电阻增大;在横向由于泊松效应的影响,重叠的石墨烯片的重叠面积增大,高电阻率面积减小,低电阻率面积增大,分离的石墨烯片实现搭接,原本不在电子迁移网络上的石墨烯片加入了网络,使得电子迁移路径的数量增多,无效片数减少,这些因素致使整个电子迁移网络电阻减小.因为橡胶泊松比,模型工作区沿纵向伸长量εl将总大于沿横向收缩量µεl,所以由模型沿纵向伸长引起电阻的增大总大于由横向收缩引起电阻的减小,从而使得模型在应变大时具有较高的电阻(图3(a)),与之对应表2 中模型工作区面积随应变升高而增大,即石墨烯片的密度随之减小,文献[20,23]表明GC 的电阻率随着石墨烯片密度升高而减小.所以尽管导致GC 产生压阻效应的具体原因有较多,但产生压阻效应的根本原因是GC 中石墨片密度的改变.
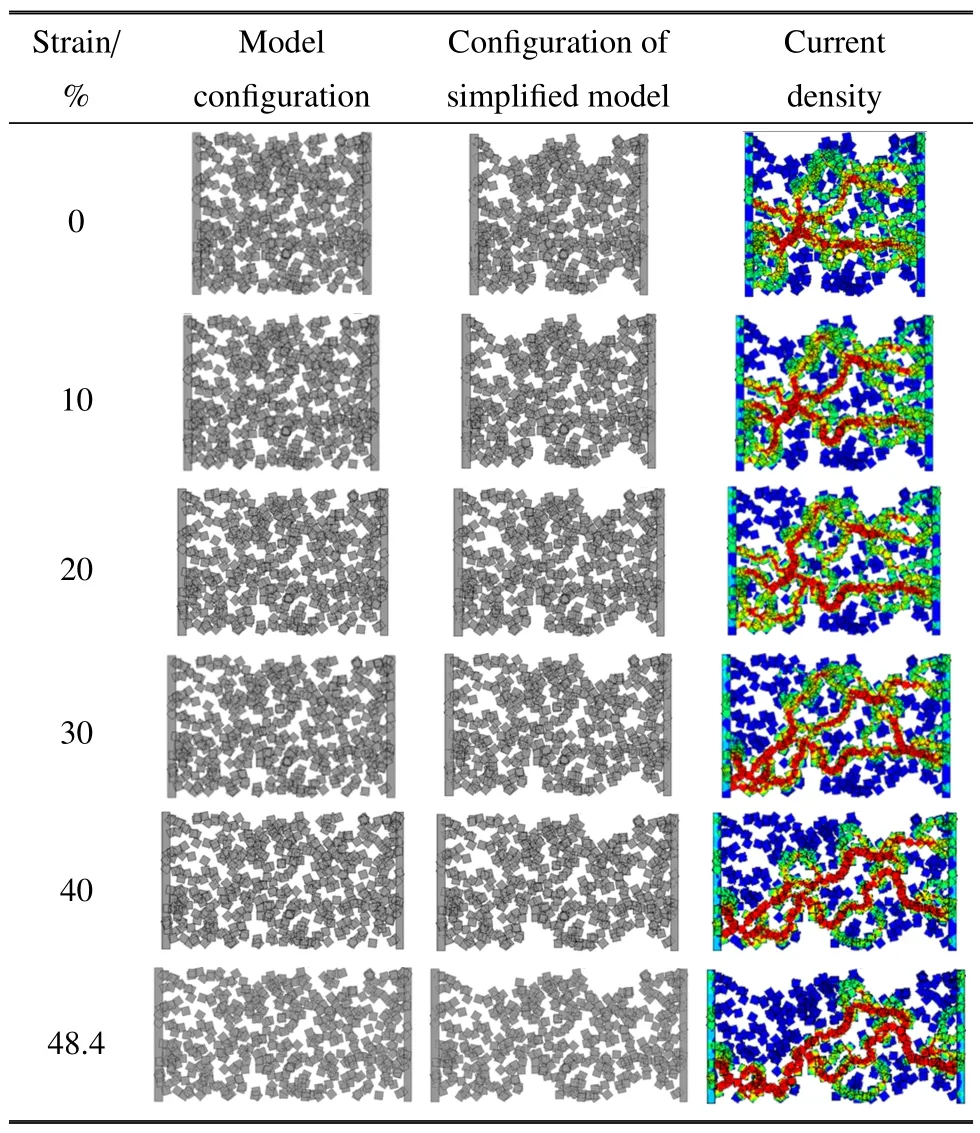
表2 传感器模型的形态与电流密度云图Table 2 Configuration and current density contour of the model
然而,我们注意到图3 中的GC 压阻性能曲线不像文献实验结果那样具有单调性,例如,当12.5% <ε<15%时,相应的石墨烯片形态与电流密度云图如表3 所示,模型没有因为石墨烯片密度的降低,出现相对电阻增大,而是由模型的横向收缩,分离的石墨烯片建立联系,使电子迁移路径数量增加,无效片减少,导致相对电阻减小.原因是上述模型中石墨烯片数过少,模型为非统计均匀场,不能反映由石墨烯片在平面内随机堆叠GC 的有效压阻性能.另外,三维GC[26]的石墨烯片与二维模型一样堆叠在基底表面,外载荷作用下,石墨烯片间同样存在滑移与分离,所以该模型的结论同样适用于三维GC.
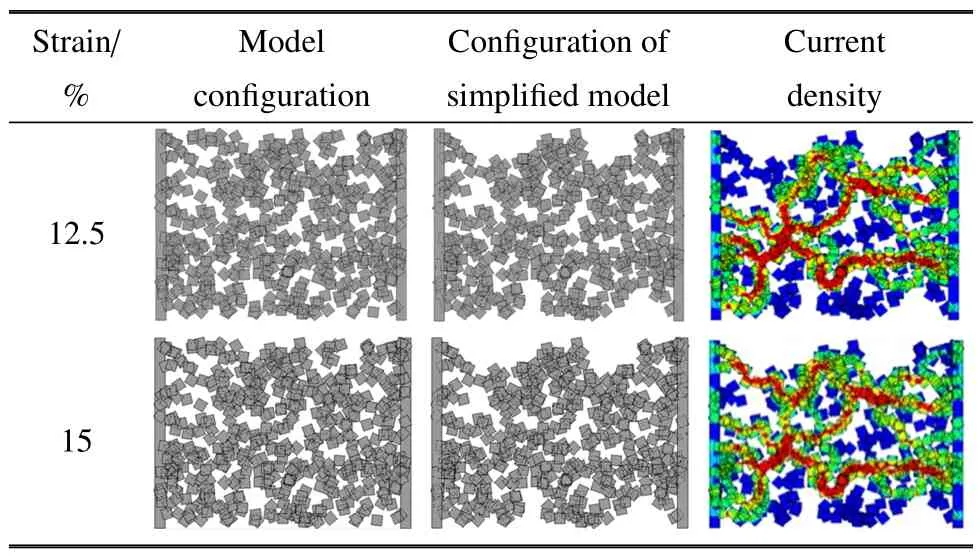
表3 传感器模型的形态与电流密度云图Table 3 Configuration and current density contour of the model
4 不同微结构GC 的压阻性能
为了探知石墨烯片的密度对GC 压阻性能的影响,工作区边长为125µm,石墨烯片边长为5µm,面分比分别为1.4,1.6,1.8,2.0 的GC 传感器模型被模拟,图4(a) 所示的模拟结果表明相对电阻曲线初始阶段近似线性变化,随着应变的增大相对电阻开始急剧增大,这是因为在变形初始,石墨烯片的滑移引起的电子迁移路径长度增长导致电阻线性增大发挥主导作用,当变形较大时,石墨烯片的分离诱发的电子迁移路径数量减少、无效片数增多致使相对电阻非线性增大开始控制电阻的走势.图4(b)中的灵敏度系数初始阶段约为3,与石墨烯复合材料滑移模型研究结论[27]一致,也能说明初始变形阶段GC 中的石墨烯片以滑移为主.因为高密度堆叠的石墨片之间拥有更多的重叠面积,模型伸长时石墨烯片导电网络具有更好的连通性,所以图4(a) 表明复合材料感知范围随着面分比的增大而提高,但是由于低密度堆叠的GC 中电子迁移网络中并联支路较少,石墨烯片的分离造成电阻的增大会首先表现出来,所以在图4(b)中它的灵敏度系数值较高.上述模拟结果与Son 等[9]和Sethy 等[28]实验结论是相同的,可证实GC 传感器模型能够模拟GC 的压阻性能.因为传感器模型最终的灵敏度系数较高,灵敏度系数β < 5时相对电阻曲线可被看作是线性的,该线性感知范围约为总感知范围的30%.

图4 不同面分比GC 相对电阻与灵敏度系数曲线Fig.4 Relative resistance and gauge factor curves of GC with different area fraction
图5 为工作区边长125 µm,面分比为1.8,石墨烯片边长分别为5µm,7µm,9µm 的模型计算结果.因为面分比相同搭接面积相近,初始电阻与滑移引起的电阻增量相仿,所以ε<60%时相对电阻与灵敏度系数曲线基本重合.当ε > 60%时,a=9µm 石墨烯片模型的灵敏度系数较小,这是因为大尺寸石墨烯片搭接长度大不易分离,也正是这个原因a=9 µm石墨烯片模型具有更大近似线性阶段与感知范围.
5 接触电阻
GC 中的石墨烯片不是平直的二维结构,而是具有很多褶皱[29],对于一些GC[18,23],石墨烯片间的接触电阻是不能忽略的.为分析石墨烯片在复合材料伸长过程中形态的变化,截取两片重叠石墨烯的局部如图6(a)所示,在复合材料伸长方向(x方向),因为石墨烯的刚度远大于基底材料,石墨烯可认为是刚性的,但在横向(y方向)由于泊松效应石墨烯片将会产生屈曲,变形过程如图6(a)∼图6(d)所示,接触面积急剧减小甚至完全分离,而Holm 电接触理论表明接触电阻与接触点的个数、接触点的半径成反比.所以石墨烯片间的接触效应,也是GC 表现出电阻随应变变化的压阻性能的一个重要原因.基于石墨烯片变形特征与接触电阻的特点,为体现接触电阻的贡献,模型中石墨烯搭接区域的面内电阻率可取为应变的函数,该函数的选取势必受到复合材料的生产工艺与传感器的制造技术的影响.

图6 变形过程中石墨烯片局部变形示意图Fig.6 Local deformation schematic of graphene flakes in the process of GC deformation
GC 相对电阻应变关系曲线通常开始阶段近似线性增长,后期急剧变大.将接触面的电阻率取为γρ0eψε/n可以展现GC 相对电阻的变化趋势,其中γ反映初始层间接触电阻的影响,若初始石墨烯片在范德华力作用下,像石墨中的石墨烯一样,虽然它的离面电阻率约为面内电阻率的110 ∼170 倍[30],但由于两片石墨烯的厚度很小,离面电阻也远小于面内电阻,可以忽略层间接触电阻的影响,γ=1,否则γ>1.ψ 体现变形对层间接触电阻影响,当变形对层间电阻影响很小时ψ=0,反之,ψ>0.图7 为工作区边长为125µm,石墨烯片边长为5µm,面分比为1.8 的传感器模型的有、无接触电阻的灵敏度系数,它表明将重叠面的电阻率取为γρ0eψε/n,可以充分体现接触效应对GC 压阻性能的贡献.

图7 有、无接触电阻模型的灵敏度系数比较Fig.7 Comparison of gauge factors between models with and without contact resistance
6 结论
本文根据GC 微观结构特征与均匀变形的特点,建立了压阻分析的力学模型,发展了压阻性能的计算方法,分析了压阻效应产生的机理和微结构参数的影响,研究结论如下.
(1)石墨烯片的滑移导致相对电阻线性变化,灵敏度系数为常数,这是GC 可作为压阻传感器材料的重要特点和优势.石墨烯片的分离致使相对电阻急剧改变,灵敏度系数不再稳定.
(2)GC 中石墨烯形态改变诱发压阻效应的根本原因是石墨烯片的密度发生了改变.
(3)高密度、大尺寸石墨烯片GC 具有较大的感知范围,边长为5µm 的石墨烯片构成的GC 线性感知阶段约占总感知范围的30%.而低密度、小尺寸石墨烯片GC 灵敏度系数更高.
(4)若需考虑石墨烯片间的接触效应,将接触面的面内电阻率设置为应变的函数,能够反映接触电阻对压阻性能的贡献.
