航天器单脉冲机动可达域求解算法1)

杜向南 杨 震

(国防科技大学空天科学学院，长沙 410073)

引言

随着人类太空活动日益频繁，空间目标(航天器、空间碎片等)数量不断增大，在轨航天器、乃至整个空间环境的安全面临新的挑战[1-2].一方面，在轨航天器存在与其他空间目标碰撞的危险[3-4]；另一方面，在轨航天器之间的对抗博弈活动越来越多[5-6]，这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7-10]，比如轨道机动后的可达范围及可能威胁区域.

航天器单脉冲轨道机动可达域是指航天器在某一位置施加机动冲量后，未来时间所有可能到达位置的集合[11].其中机动冲量满足一定约束条件[12]，一般用速度机动球或速度机动椭球来描述，用以限制脉冲机动的大小和方向.

航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来.导弹攻击区[13]是指导弹攻击目标的可能范围.Beckner[14]给出了基于椭圆轨道上某点发射弹道武器，发射速度固定情况下的可达区计算公式.Battin[15]进一步研究并给出弹道导弹在初始静止、发射速度方向任意，大小受限情况下轨道可达包络的确定方法.随着航天技术发展，基于天基平台的导弹拦截受到一定关注，1994年，Vinh 等[16-17]采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题.常燕等[18-19]提出了追踪区的概念，用于描述满足约束的可行变轨点集.徐加瑞等[20]对追踪区和机遇区进行了进一步研究.随后，可达域研究进一步向具有空间机动能力的航天器拓展.2009 年，雪丹等[21-22]提出了航天器可达范围的概念，在不考虑拦截目标和时间约束情况下，研究航天器所有可能到达的最大区域，文献[23]给出了共面可达范围的精确求解，主要针对二维平面情况，此后作者在文献[24]中进一步研究了三维空间的可达范围求解方法，但是该方法仅能给出可达范围的保守上界，不能精确地确定可达范围.针对此不足，温昶煊等[25-28]通过参量转化进一步研究了三维空间可达域问题，该方法通过分别计算内外包络获得可达域，但求解模型较为复杂，涉及较多的变量代换关系；陈奇等[29]基于初始轨道建立模型，通过增加几何约束条件，求解非线性方程组获得了航天器单脉冲机动的可达域包络，进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算，温昶煊等[25-28]的方法计算操作简单，但求解模型的可达性证明较复杂，涉及复杂的角度转化关系证明，且针对可达域内外包络有不同的计算公式；陈奇等[29]的方法模型普适性更好，但是非线性方程组求解对初值选取的要求较高，初值选取不合适会使得部分计算结果偏保守从而导致精度降低.因此需要模型更加精简，拟合效果更好的求解算法.

针对现有研究不足，本文基于近心点坐标系建立了针对未来可达位置矢量极值求解的可达域求解模型.首先基于边界速度双曲线推导可达性判断条件；其次在待求位置指向可达前提下，构建可达矢径极值求解算法，求解基于单一参变量的非线性方程，获得可达域包络位置坐标；最后采用Monte Carlo 打靶仿真方法验证所提方法的正确性.

1 可达域求解模型

1.1 坐标系定义

令r0表示航天器初始位置矢量，rf表示航天器终端位置矢量，如图1 所示，航天器在r0处执行一次机动，经转移轨道到达rf.由r0，rf可确定转移轨道平面M，设该平面与初始轨道平面夹角为β.

定义近心点坐标系Sg：原点E位于地心，xg轴指向初始轨道近地点，zg轴指向初始轨道角动量方向，yg轴位于初始轨道平面内，并与xg，zg轴构成右手直角坐标系.设初始轨道航天器机动位置的真近角为f，则r0在Sg坐标系下表达式

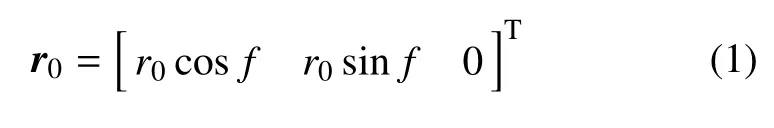
其中r0表示初始位置矢量r0的长度.

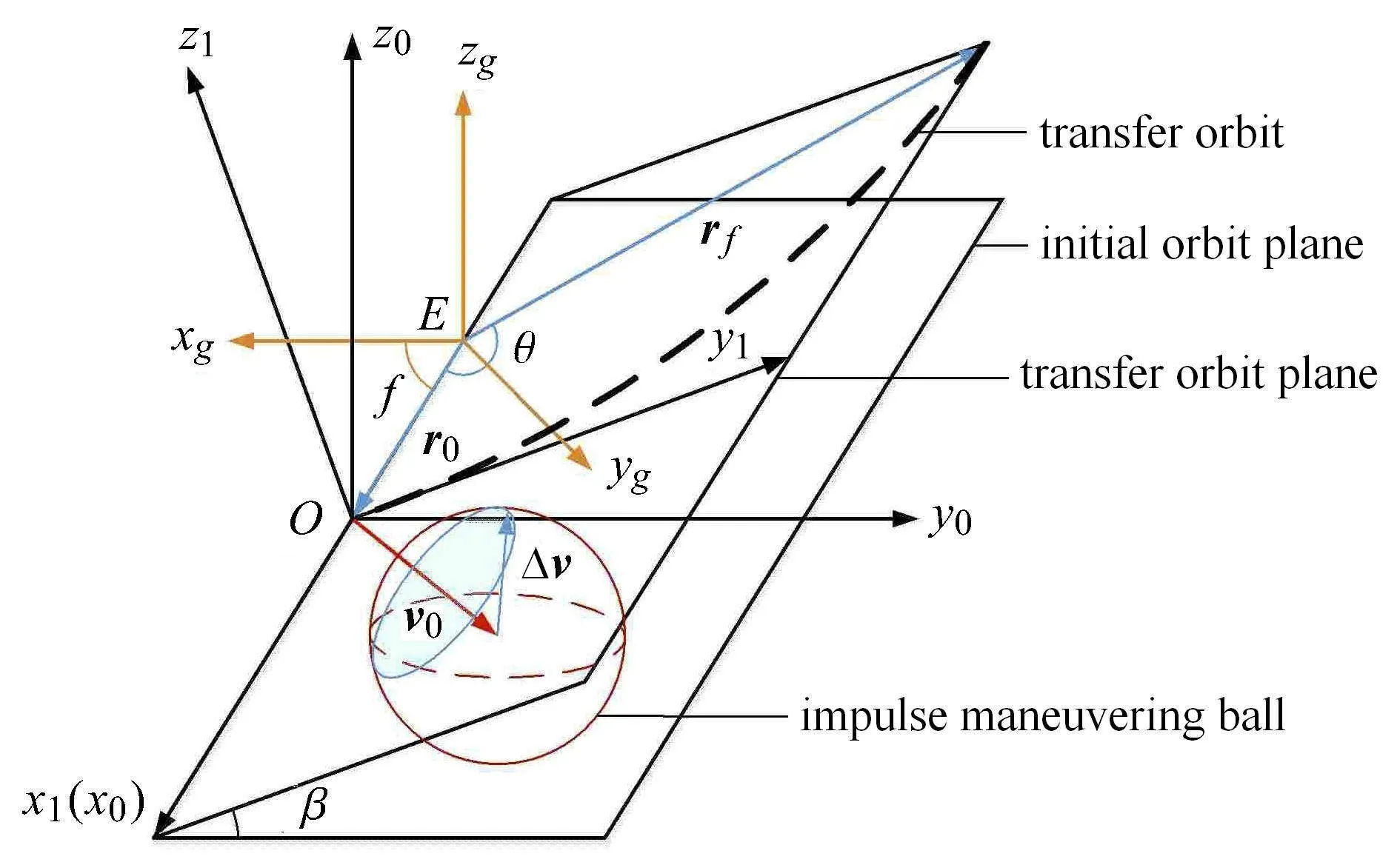
图1 坐标系位置关系Fig.1 Illustration of the defined coordinates

定义坐标系S0：原点O位于航天器质心，x0轴与r0重合，z0轴指向初始轨道角动量方向，y0轴与x0轴、z0轴构成右手直角坐标系.航天器初始轨道速度v0在S0坐标系下可表示为[11]

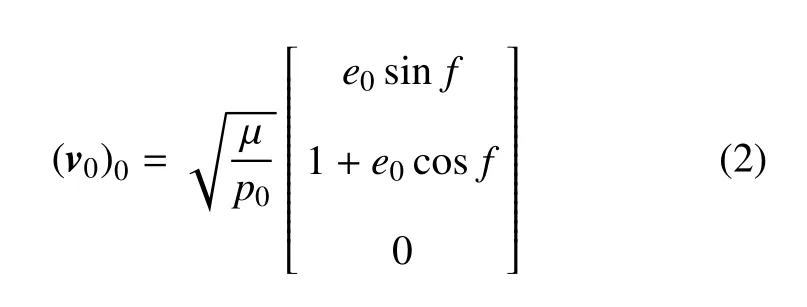
定义轨道坐标系S1：x1轴与x0轴重合，z1垂直于平面M并指向转移轨道角动量，y1位于M面内，与x1，z1构成右手直角坐标系.航天器初始轨道速度v0在S1坐标系下可表式为

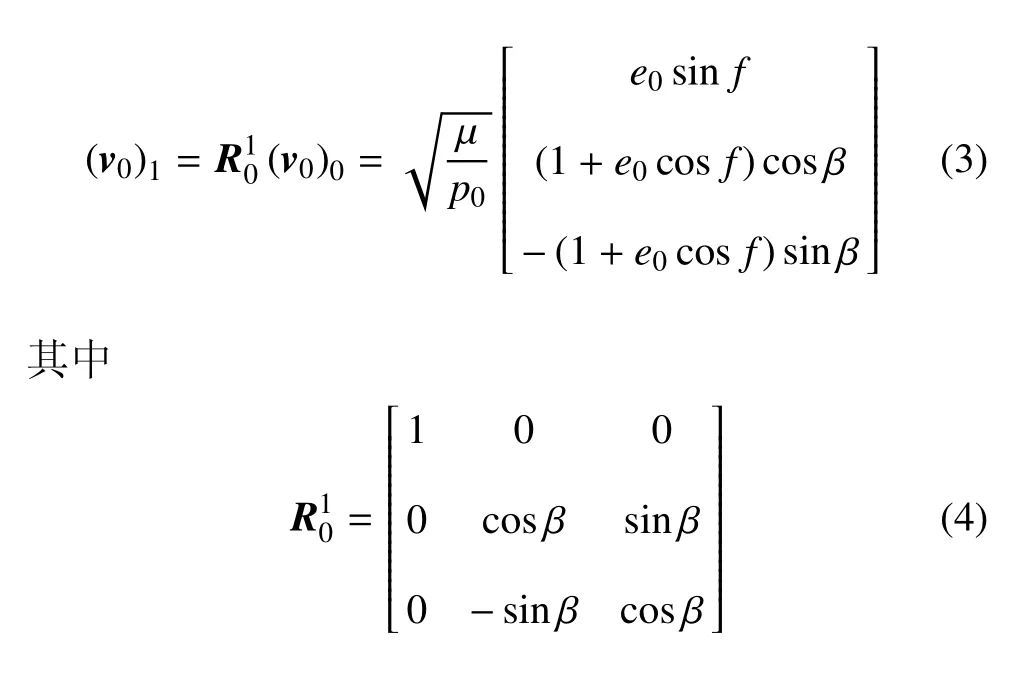
一般而言，航天器携带的推进剂有限，其最大机动能力亦有限，可以转化为总速度增量∆v表示.假设航天器最大机动能力为∆v，机动方向任意，即可将航天器的机动能力建模为速度机动球.如图2 所示，在速度机动球内，航天器执行某一可能的机动后，将进入M平面内的某一对应转移轨道，到达rf位置.定义∆vM为∆v在转移轨道面内的投影，用角度α 表示∆vM相对于参考方向=r0/r0的夹角，即转移轨道面机动方位角.

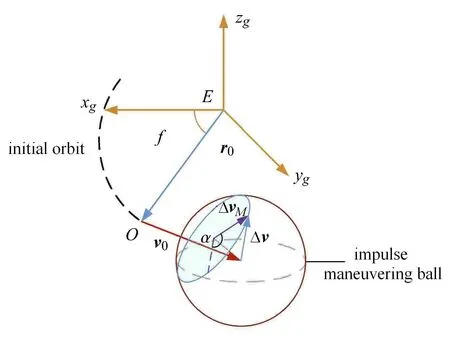
图2 速度脉冲方位角Fig.2 Azimuth of the maneuvering impulse

记航天器机动后的速度为v1=v0+∆v，根据S1坐标系定义，v1在S1中可表示为

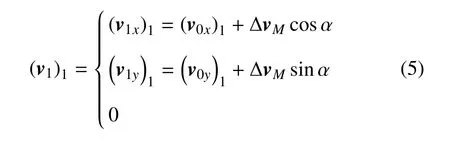
在近心点坐标系Sg中，定义角度γ 与ϕ，用来描述机动后未来可达位置矢量rf的空间指向，如图3 所示.图中ϕ 表示rf与初始轨道面的夹角.rf在初始轨道面内的投影用线段EW表示，E为引力中心，W为初始轨道上某点，γ 表示rf在初始轨道面投影EW与xg轴之间的角距，即近心点角距.显然，γ 与ϕ 取值变化可使rf指向空间任一方向，而该指向在给定速度机动约束条件下是否可达，需要进一步验证并给出可达性判据.

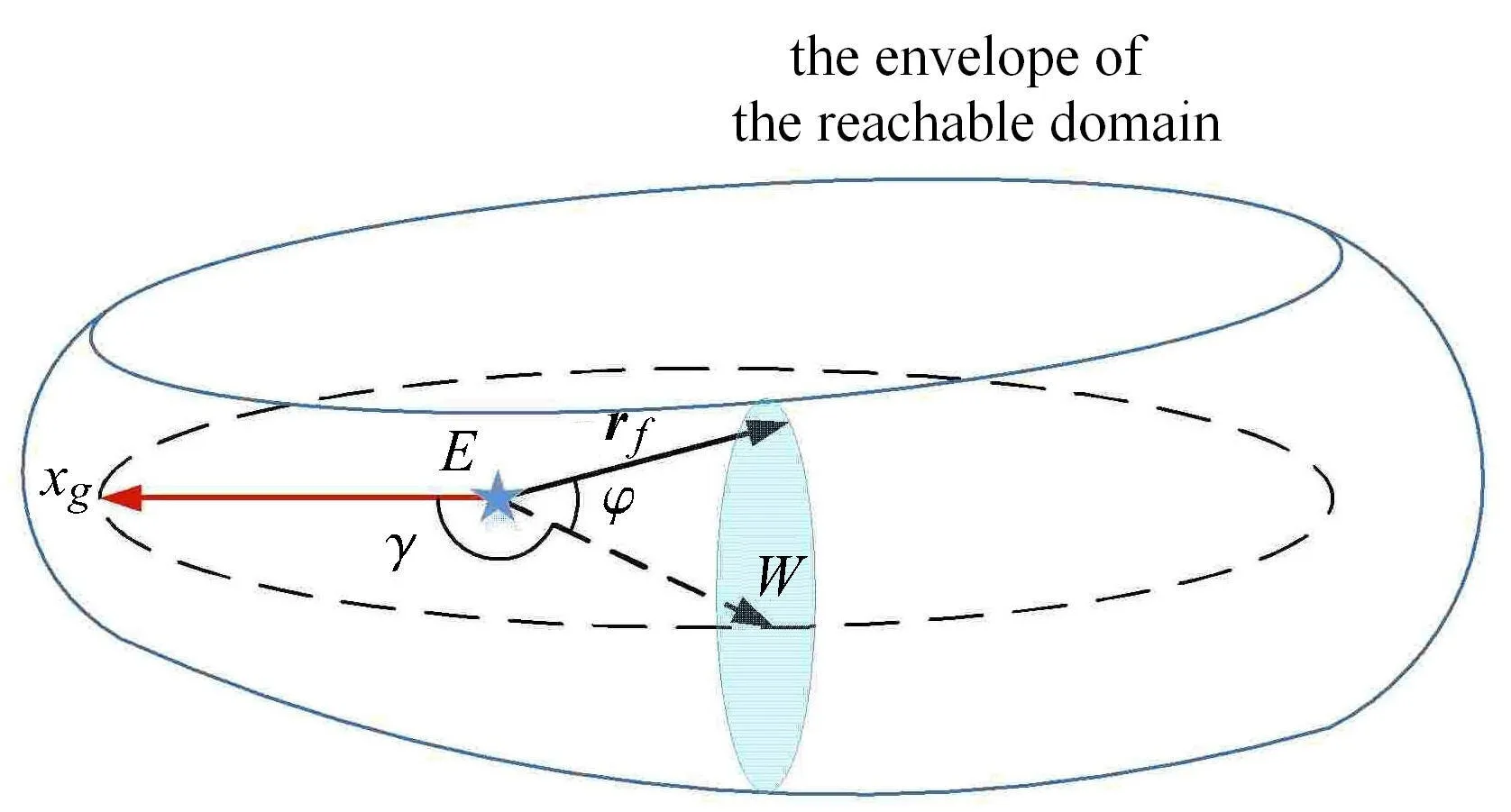
图3 γ 和ϕ 角度示意图Fig.3 Illustration of angle γ and ϕ

1.2 轨道机动可达性判据

以轨道机动位置r0为起点，终端位置rf为终点，二点之间的转移过程可以看做是两点边值问题，Battin[15]证明轨道两点边值问题满足如下等式

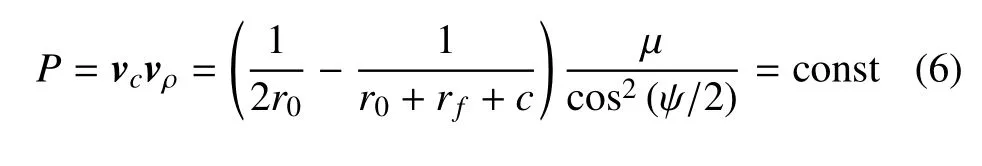
定义从机动位置到目标位置的弦为c=rf−r0，式(6)中vc,vρ分别表示S1中坐标系下转移轨道初始速度矢量v1在弦长方向和r0方向的速度分量，为连接r0和rf的弦长，ψ 表示vc与vρ之间的夹角，如图4 所示.

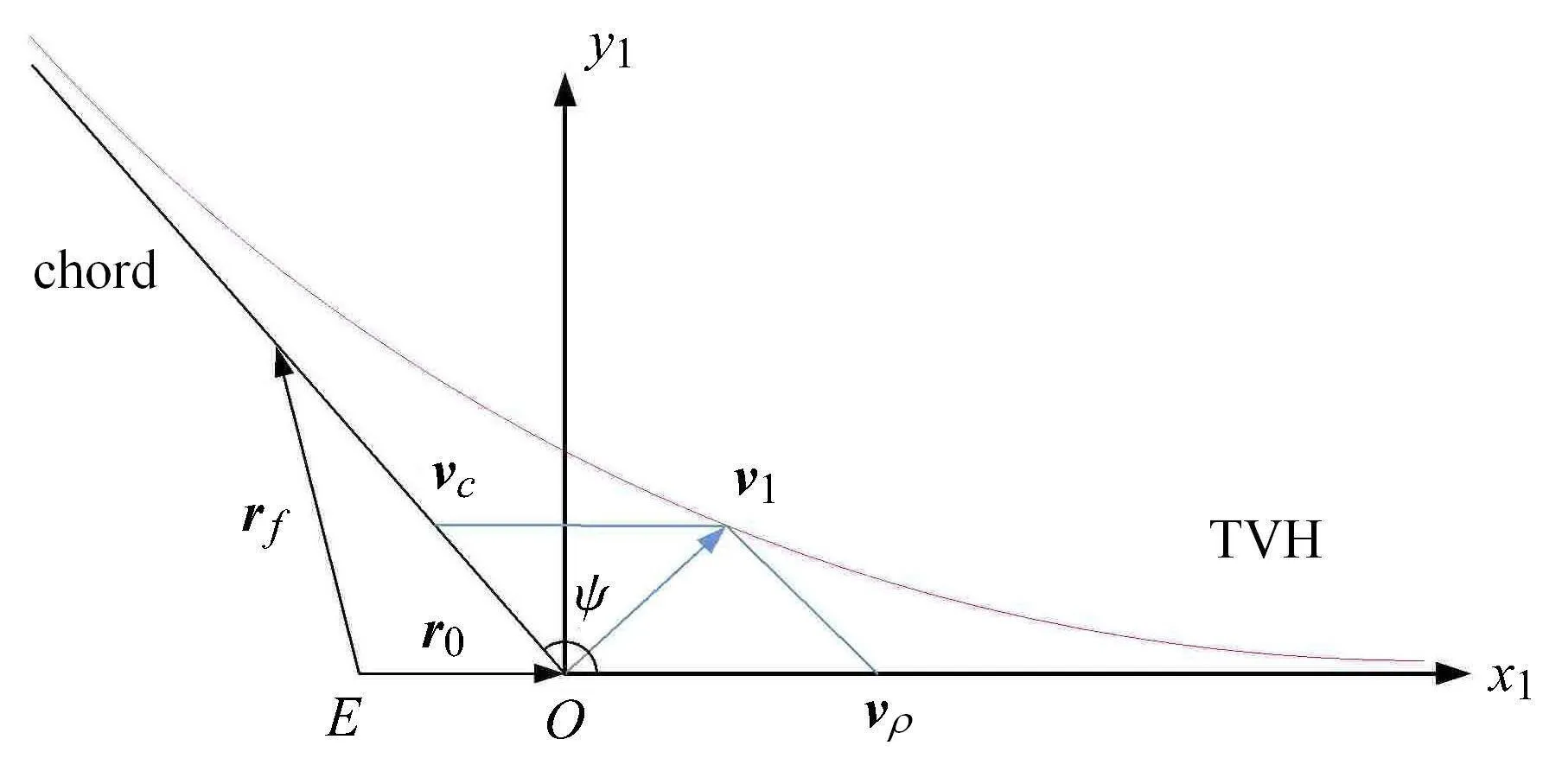
图4 边界速度双曲线示意图Fig.4 Illustration of terminal velocity hyperbola

由等式(6)可得轨道两点边值问题的重要结论[15]：能到达给定目标位置矢量的所有可能转移轨道，其初始速度矢量的轨迹是一条边界速度双曲线(terminal velocity hyperbola，TVH)，该双曲线两条渐近线分别为弦和初始位置矢量r0所在的直线.因此，为使得rf目标方向可达，需保证机动后的速度始端能够落在边界速度双曲线上，如图5 所示.

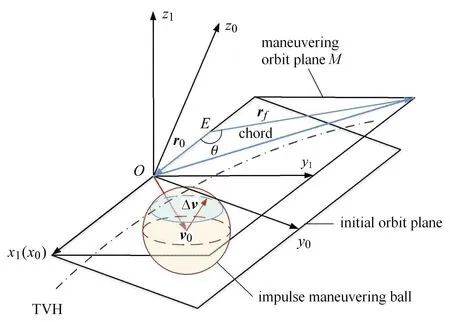
图5 边界速度双曲线与速度机动球关系Fig.5 Relationship of TVH and impulsive maneuvering ball

当[γ,ϕ]确定后，rf的指向随之确定，随着rf矢径长度变化，TVH 渐近线走势也随之变化，从而可以得到一簇边界速度双曲线，该双曲线簇随rf长度变化可覆盖整个转移轨道平面M，如图6 所示.因此，只需保证转移轨道面与速度机动球相交，即可保证机动后速度矢端落在边界速度双曲线上，从而使得rf目标方向可达.

图6 边界速度双曲线在M 平面内分布Fig.6 Distribution of TVH in the plane M

若要使得转移轨道面与速度机动球相交，只需保证速度脉冲∆v在转移轨道面内存在分量∆vM，由图7 可知∆vM可由下式求解

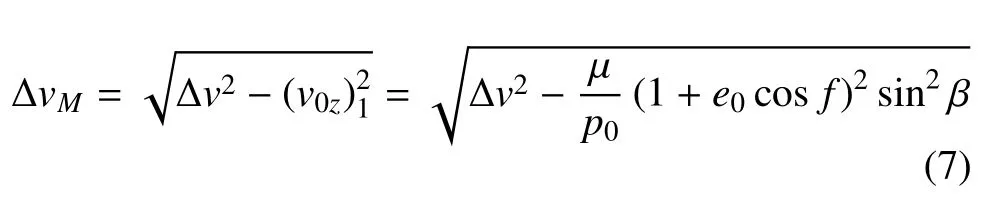
为使式(7)可解，需保证式中根号下表达式非负.式(7)中角度f,γ,ϕ,β 的几何关系如图8 所示，由空间几何公式可知

将式(8)代入式(7)，令式(7)中根号下表达式非负得到

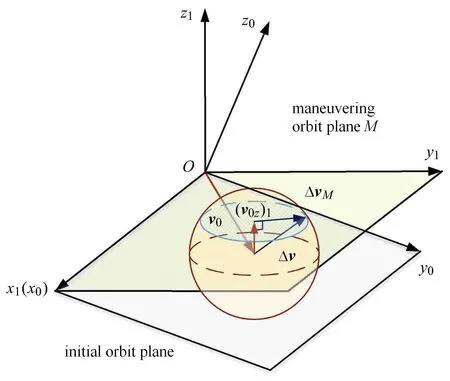
图7 ∆vM 位置关系Fig.7 Location of ∆vM

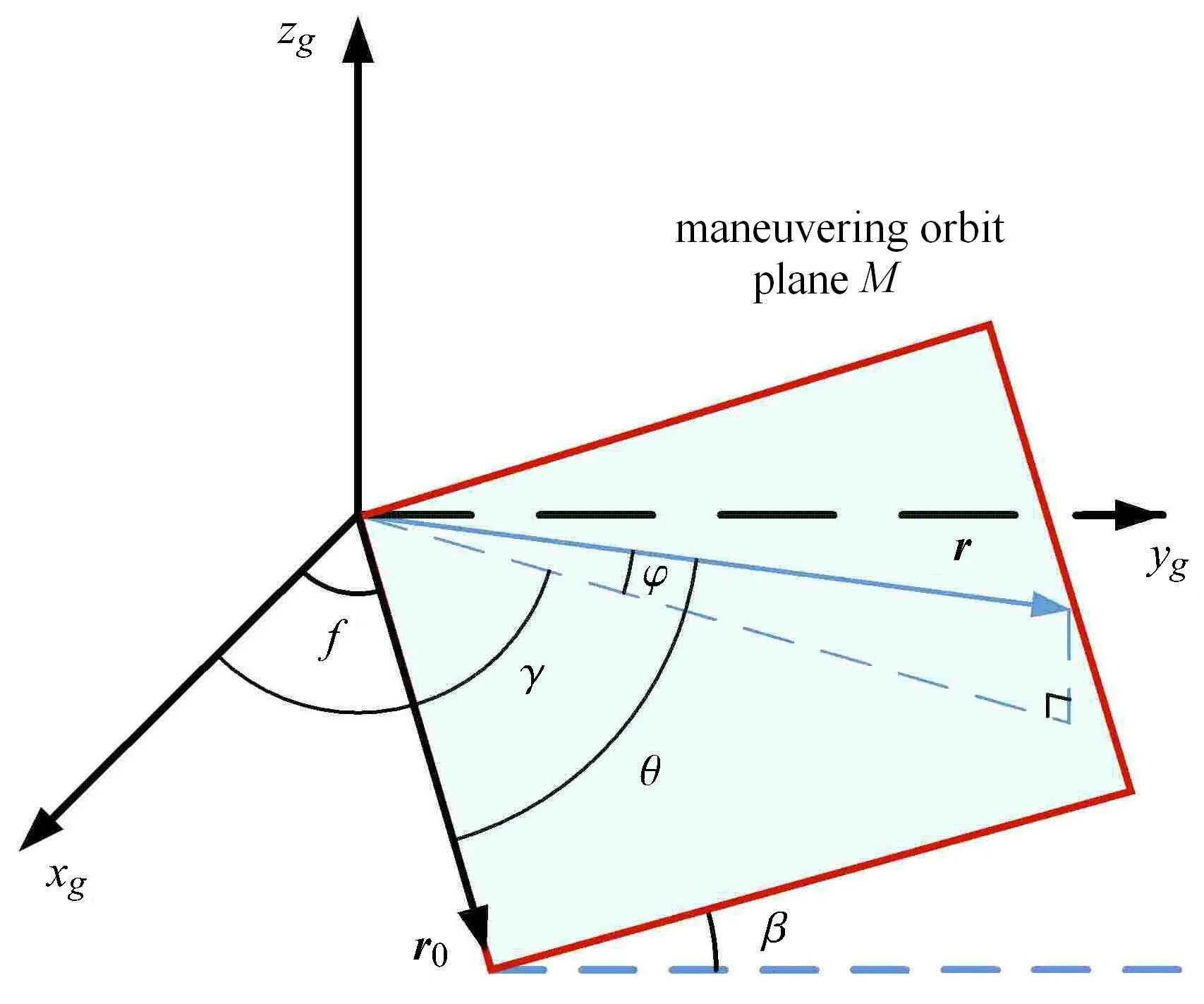
图8 角度几何关系Fig.8 Geometry of the defined angles

进一步整理式(9)得到可达性判据，ϕ 应满足

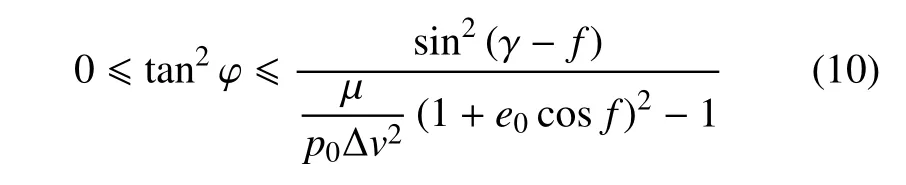
当rf与r0共线时，此时γ−f=0 或γ−f=π，ϕmax=ϕmin=0.对rf与r0不共线的一般情况，当rf方向可达时，取纵向切面如图9 所示，根据可达性判据，ϕ 存在取值范围[ϕmin,ϕmax]，极值ϕmin,ϕmax分别对应rf与可达域上下两端相切的情况.一般情况下，rf会穿过可达域得到一条可达线段UV.EU对应rf方向可达矢径的极小值，EV对应rf方向可达矢径的极大值.因此，获得轨道机动可达性判据后，求解轨道机动可达域包络的核心问题是如何计算所有可达方向的矢径极值，本文将在2.1 节给出求解算法.

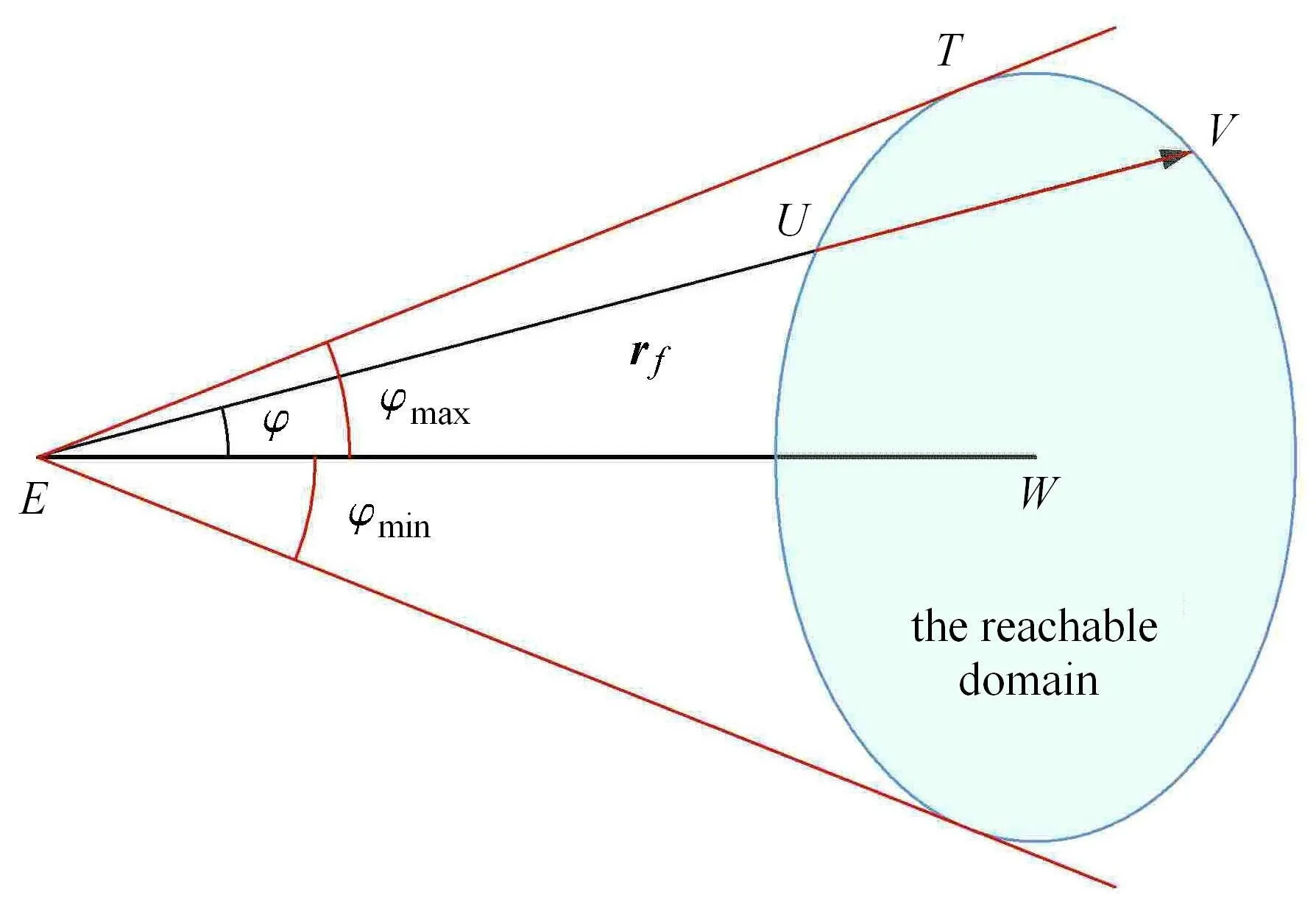
图9 可达线段UVFig.9 The reachable line UV

1.3 可达域包络的几何特性

如图10 所示，在S0坐标系下，速度机动球关于初始轨道平面对称，令∆v1，∆v2为两个对称的速度机动冲量，显然机动后速度矢量vt1，vt2也关于初始轨道平面对称，有

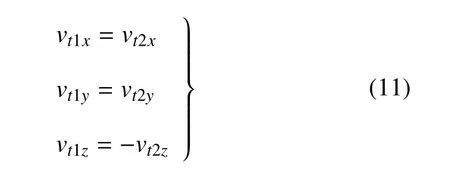
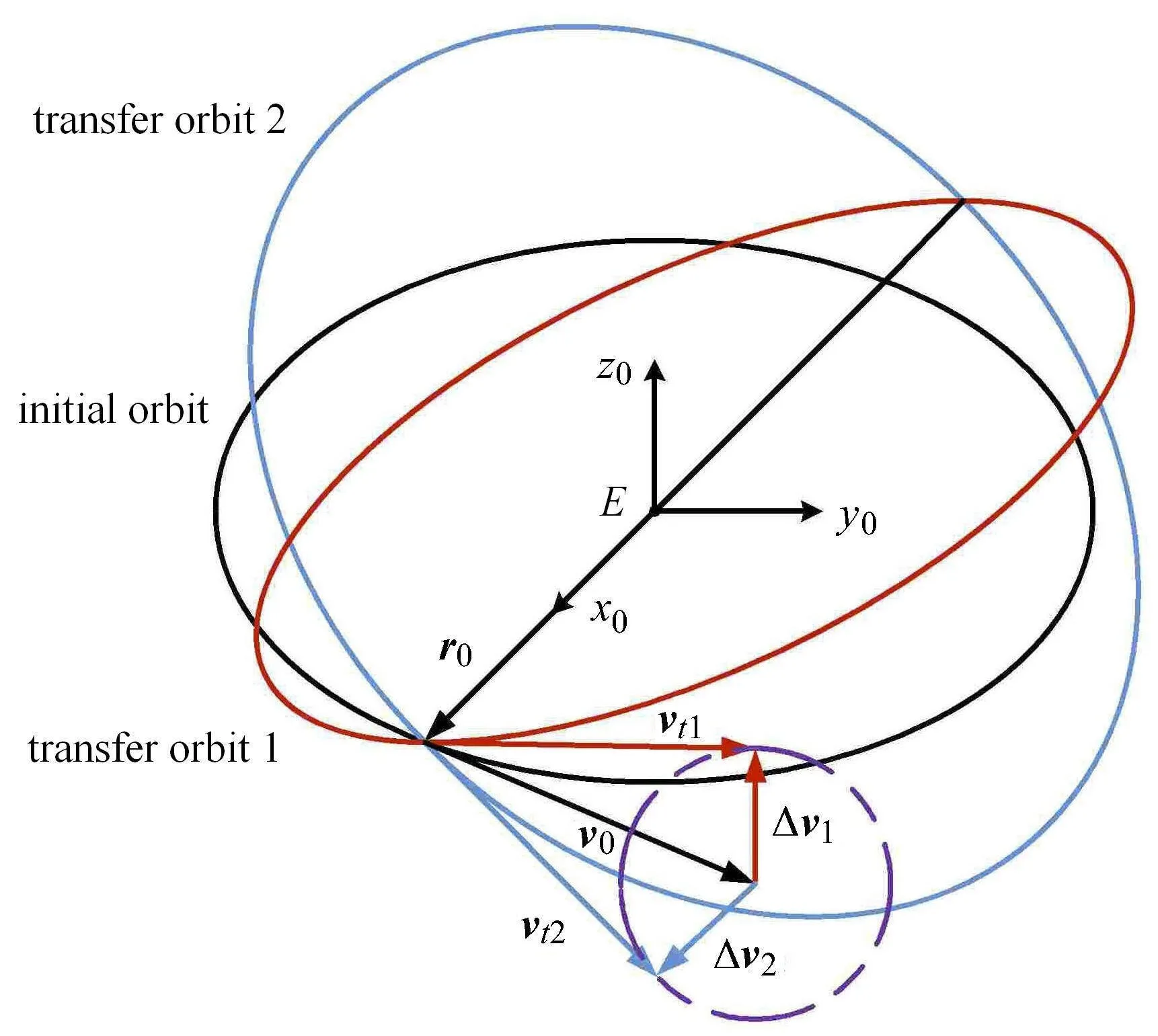
图10 转移轨道对称性Fig.10 Symmetry of transfer orbits

在二体轨道初值问题中，设经过一段时间后，两条轨道的位置相对于初始位置的真近角差均为∆f，则该时刻轨道位置可以表示为[30]

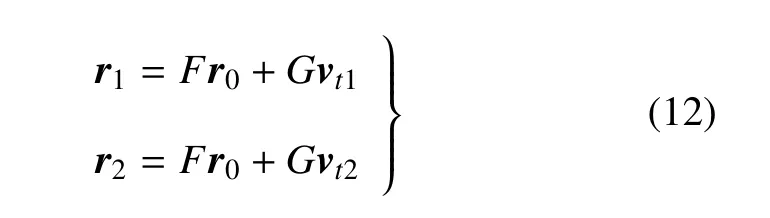
其中，F与G为拉格朗日系数，仅与∆f取值相关[30]，当∆f相同时，可作为常系数处理.

若不采取任何机动，航天器自由运行到距离初始位置真近角差∆f处的轨道位置可以表示为

如图10 所示，在S0坐标系中，x0Oy0平面是基于初始轨道面建立的，因此r0z=0；v0z=0，从而式(13)中

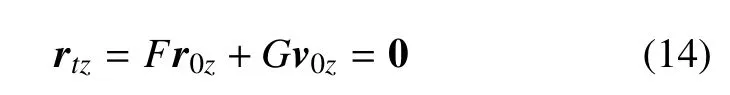
因此由式(11)∼式(14)可知

根据上述结论可知，r1和r2始终关于初始轨道面(z0=0)上下对称.由于单脉冲机动可达域是上述对称轨道分布的区域，因此也是关于初始轨道面对称的.

因此，在二体轨道假设下，求解轨道机动可达域，只需计算位于初始轨道平面一侧的可达域包络，可达域的另一半可由对称性快速获得，如图11 所示.

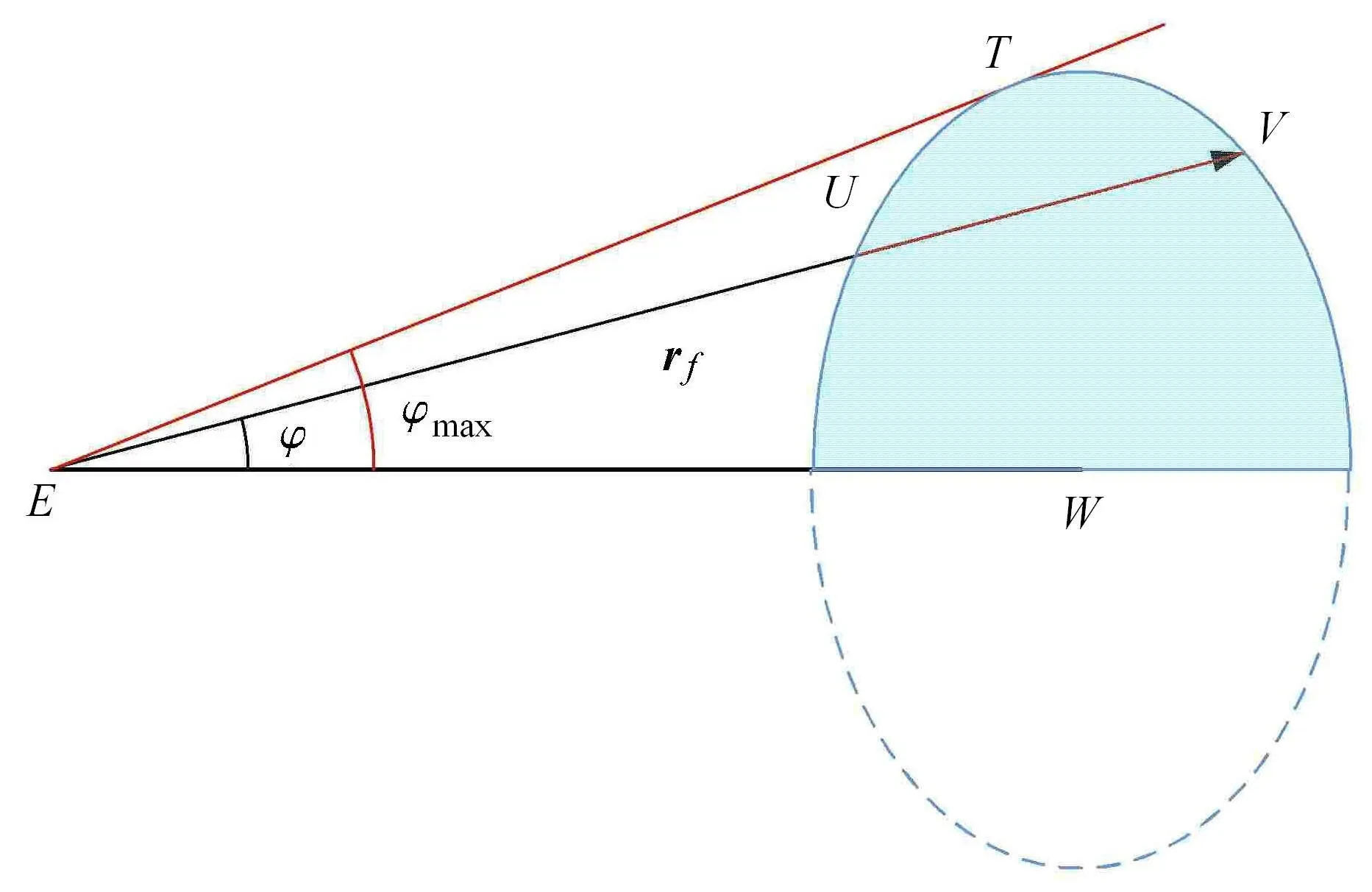
图11 可达域包络对称性Fig.11 Symmetry of reachable domain

2 可达域求解算法

由第1 节可达域求解模型可知，求解航天器单脉冲轨道机动可达域的核心是按照一定顺序求解航天器在[γ,ϕ]方向上可达矢径的极值.本节介绍可达方向矢径极值求解算法，给出完整求解流程，并与两种已有算法流程对比，说明本算法改进之处.

2.1 可达方向矢径极值求解算法

基于二体轨道动力学模型可得目标位置矢量rf可表示为[25]

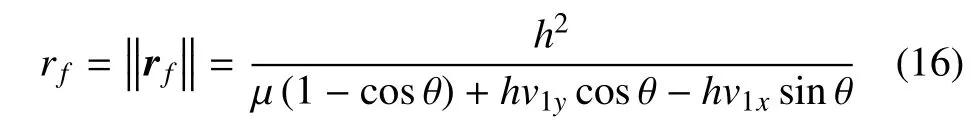
式中，θ 表示r0与rf的夹角；h=，其中h表示转移轨道角动量

θ 可由图7 角度关系表示

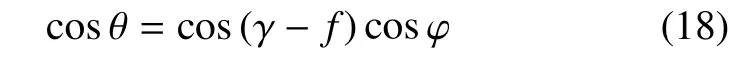
根据γ 和f的位置关系，进一步确定θ 的取值范围如下

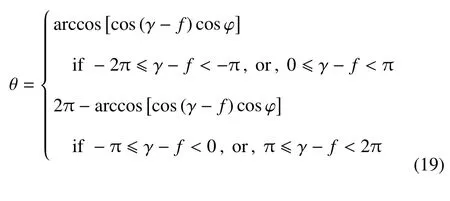
将式(3)代入式(5)可知vx，vy是关于β 和α 的函数，又由式(6)可知i是关于γ 和ϕ 的函数.因此，rf矢径可以表示为

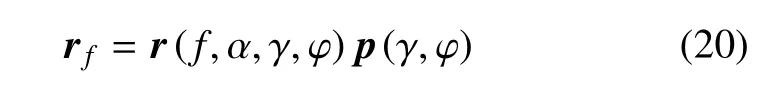
其中rf表示rf矢径大小，p表示rf方向单位矢量

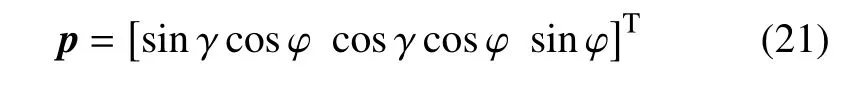
当机动位置f，终端位置方向γ,ϕ 确定后，rf矢径式(20)是关于变量α 的一元函数，因此只需选择合适的α 取值，使得式(16)取极值即可.式(16)对α 求导得

将式(3)代入式(5)，并对α 求偏导得

将式(23)代入式(22)得到

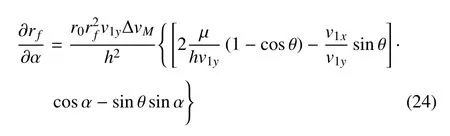
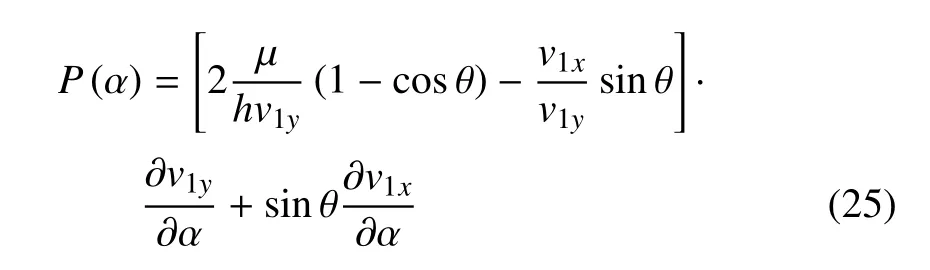
则可将极值求解问题转化为求表达式P(α)=0 的零点的问题.求解完成后，将所得α 解代入式(16)即得到rf矢径极值.

在满足可达性判据的前提下，终端位置rf方向上可达位置点构成可达线段UV，如图12 所示.EU和EV是rf矢径两个不同的极值，因此，在[−∞,+∞]范围内，至少存在两个α 值满足式(25).

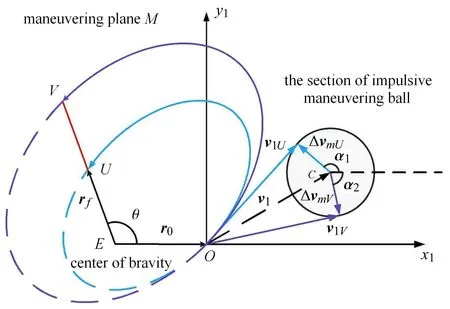
图12 ||rf||极值与α 取值关系Fig.12 Relationship between||rf||and α

在采用数值迭代法求解式(25)的零点时，不同的迭代初值会得到不同的α 可行解.对于式(16)，只需从这些可行的α 取值中选取两个，能够分别对应rf矢径的极大值和极小值即可，本文迭代计算的初值按照下式给定

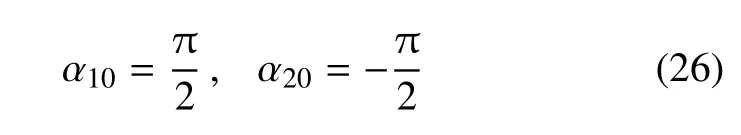
按照式(26)中两个初值分别迭代求解，可以得到两个备选的可行解α1,α2，分别代入式(16)，得到rf1和rf2，将两个的值中较大的记为rfmax，较小的记为rfmin.通过式(27)进一步计算Sg坐标系下的极值点位置坐标

2.2 可达域求解流程

本文可达域算法求解流程如算法1 所示.γ 在[0,2π]范围内取值,ϕ 在[−π/2,π/2]范围内取值,由1.3 节包络对称性，可以缩小ϕ 计算范围至[0,π/2].

最近，温昶煊等[25-28]、陈奇等[29]对单脉冲轨道机动可达域问题进行了研究，温昶煊等的方法通过证明转移相位角和速度机动方向的对应关系，分别针对可达域内外包络建立了可达域直接求解模型.陈奇等的方法以初始轨道为基础，将可达域定义为围绕在初始轨道周围的管道模型，并给出了通过求解非线性方程组计算可达域的方法.为便于对比分析，本文将这两种方法的求解流程简要总结如算法2 和算法3 所示，其中温昶煊方法记为已有算法一，陈奇方法记为已有算法二.

算法1本文可达域算法求解流程

步骤1：给定初始轨道参数，由式(1)计算r0.

步骤2：γ 在[0,2π]范围内任意取值，ϕ 在[0,π/2]范围内任意取值，由式(21)确定单位矢量p.

步骤3：根据式(10)判断当前方向是否可达，若不可达则返回步骤2 重新取值.

步骤4：由表达式(25)迭代计算使当前rf方向矢径取极值的α 取值，迭代初值按照式(26)确定.

步骤5：将式(16)计算rf方向矢径极值.

步骤6：将矢径极值和当前方向矢量p代入式(27)计算极值点在Sg坐标系中的位置坐标.

步骤7：重复步骤2 至步骤6 直至角度序列[γ,ϕ]覆盖整个空间范围，将所有极值点坐标汇总得到可达域.

算法2已有算法一求解流程[25]

步骤1：确定转移轨道面倾角i的允许上下界，imin和imax，θ 允许取值范围[0,2π].

步骤2：计算中间参量F(i)和Q.

步骤3：求解中间变量αc，απ1，απ2.

步骤4：确定α 和θ 之间的转化关系θ(α)，按照内包络与外包络分为θin(α)和θout(α).

步骤5：由αc确定α1,α2，定义[α1,α2]对应远地包络，定义[α2,α1+2π]对应近地包络.

步骤6：求解可达域远地包络：

(a) 在[α1,α2]区间内任取角度α，由θout(α)计算θout;

(b)由α,θ 计算包络半径r，并确定远地包络坐标;

(c)重复步骤(a),(b)直至α 覆盖区间[α1,α2].

步骤7：求解可达域近地包络：

(a)在[α2,α1+2π]区间内任取角度α，由θin(α)计算θin;

(b)由α,θ 计算包络半径r，并确定近地包络点坐标;

(c)重复步骤(a),(b)直至α 覆盖区间[α2,α1+2π].

步骤8：重复执行步骤2 到步骤7 直至角度i覆盖整个区间[imin，imax].

算法3已有算法二求解流程[29]

步骤1：给定初始轨道参数，确定r0和h0.

步骤2：α 在[0,2π]范围内任意取值，ϕ 在[0,2π]范围内任意取值.

步骤3：由正弦定理确定控制变量λ 和κ 满足的约束关系G(λ,κ)=0.

步骤4：将极值表达式R(λ,κ)分别对λ 和κ 求偏导，得到两个非线性方程H1=0,H2=0.

步骤5：确定初值λ0和κ0，求解方程F=[G H1H2]=0.

步骤6：将所求λ 和κ 的值代入矢径极值表达式，并转化为在坐标系下的坐标形式.

步骤7：重复执行步骤2 到6 直至角度i覆盖整个空间.

由算法1 ∼算法3 可知，针对单脉冲轨道机动可达域求解问题，两种已有算法与本文算法相比，相同之处是3 种算法均设置了两个角度变量，用于描述未来可达位置矢量rf的指向，角度变量定义各有不同：算法2 定义了转移轨道面倾角i和转移轨道面的转移相位角θ 用以描述rf指向；算法3 定义了角度α 描述初始轨道上某点的位置，定义角度ϕ 表示以该点为起点的空间指向；本文提出的算法1 定义两个角度γ 和ϕ 分别表示rf相对于xg轴的方位角和相对初始轨道面的俯仰角.综上，无论采用哪种角度定义方式，均可使rf指向空间任意方向.

3 种算法的不同之处在于：算法2 首先确定一个变量i的取值范围，然后按转移轨道的未来走势不同把另一个变量α 在[0,2π]范围内分类，分别求得可达域内包络和外包络；算法3 是对每一个目标方向[α,ϕ]，用数值方法求解关于λ,κ 的非线性方程组，求得控制变量λ,κ 的解后回代入可达矢径表达式求得可达域包络；而本文算法1 设计了不同的方向序列选取方案，提出了更加简洁的可达性判定方法，将可达域内外包络的求解统一为通过对单一变量求解非线性方程得到，相对于算法2 和算法3 均有所改进.与这两种已有算法对比，本文方法的优势在于：(1)相比于算法2，不涉及复杂的变量关系推导，模型更加简单；可达性证明及可达性判据的推导过程更加简洁，并且将内外包络的计算方法进行了统一.(2)相比于算法3，虽然两者都需要采用数值方法进行求解，但是本文只有一个待求参数，不需要求解微分方程组，初值敏感性低，求解效果较好.

3 仿真分析

本节以二体模型下椭圆轨道为例，计算航天器单脉冲机动可达域，采用Monte Carlo 打靶仿真验证本文方法的正确性，并将两种现有算法与本文算法求解结果进行对比分析.仿真算例采用的初始轨道参数:半长轴a=107m,轨道倾角i=0 rad,偏心率e=0.2,机动位置f=π/3 rad.最大速度脉冲|=500 m/s，方向任意，即机动冲量限制在一个半径为500 m/s 的空间球体内，如图13 所示.

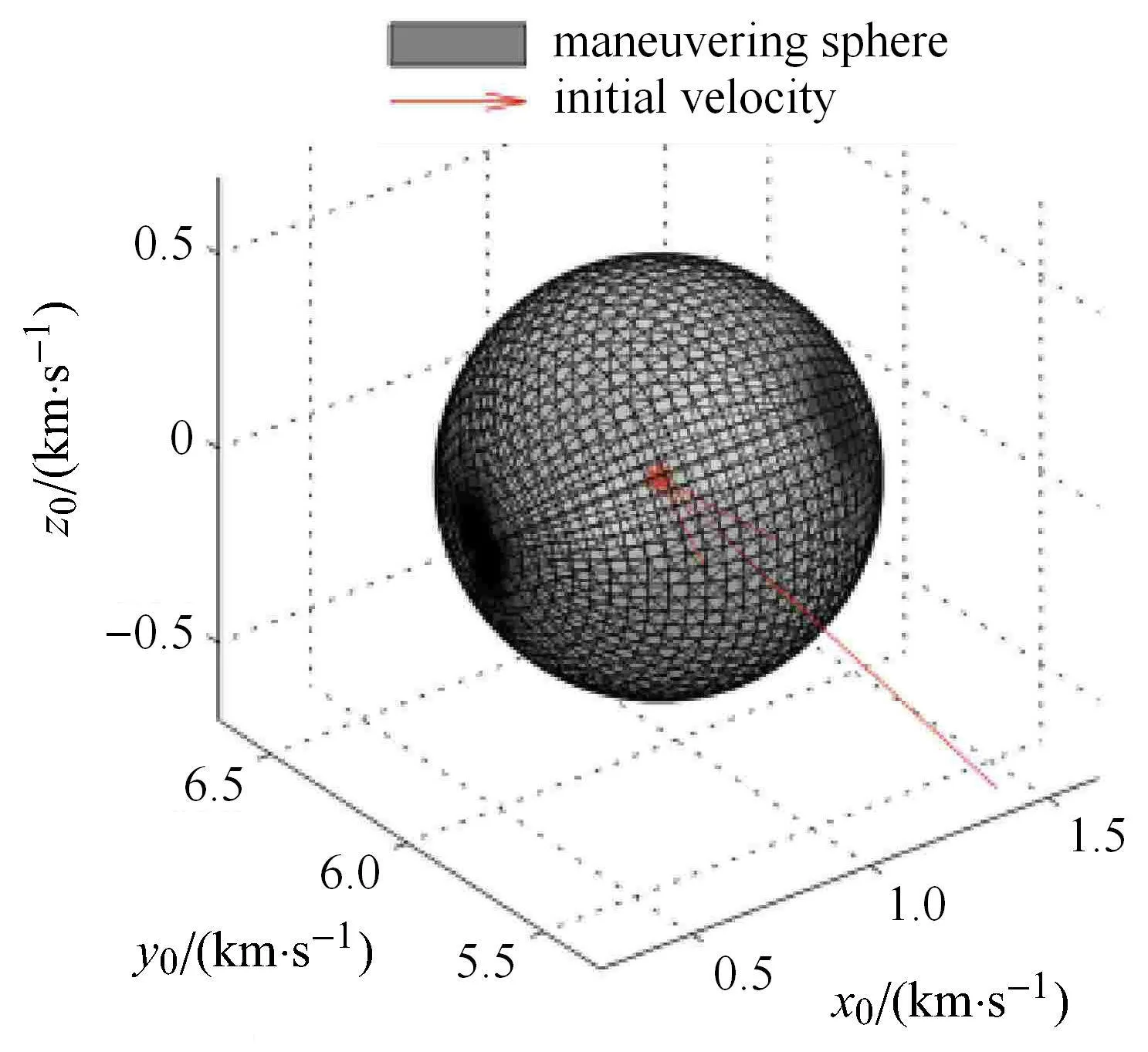
图13 速度机动球||∆v||=500 m/sFig.13 Impulsive maneuvering ball||∆v||=500 m/s

Monte Carlo 仿真的具体实施如下：

(1) 如图14 所示，在f0=π/3 处，对脉冲机动大小∆v、机动方向角度δ,ξ，采用均匀分布随机选取10 000 个样本点；

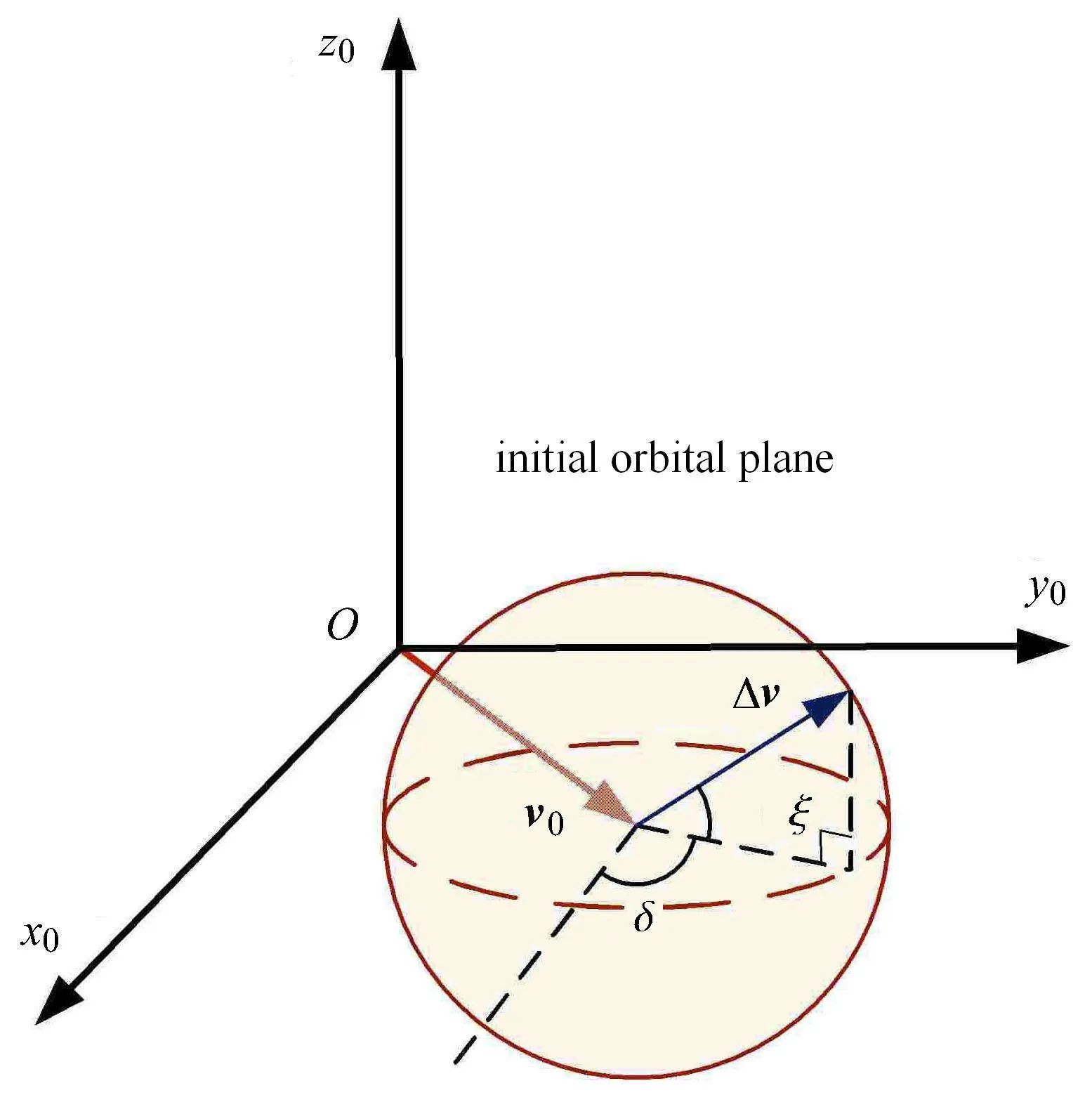
图14 机动方向角度δ 和ξFig.14 Maneuvering angle δ and ξ

(2)将每一次样本机动量添加到航天器初始速度部分，采用二体轨道模型将初始位置速度外推一个轨道周期，得到一条机动后的样本轨道；

(3)采用本文算法求解轨道机动可达域包络，通过观察所有机动后样本轨道是否完全落在求解的可达域包络内来判定求解结果的正确性.

3 种算法的计算结果如图15 ∼图17 所示.需要说明的是，已有算法一求解过程不涉及数值迭代；已有算法二涉及非线性方程组数值求解，本算例中将初值取为λ0=π/2，κ0=0；本文所提算法所涉及非线性方程数值求解，算例中将初值取为(α0)1=π/2 及(α0)2=−π/2，分别对应该方向两个矢径极值的求解.图15 ∼图17 中，黑色实线网格为不同算法对可达域包络的求解结果，青色虚线为Monte Carlo 仿真结果.

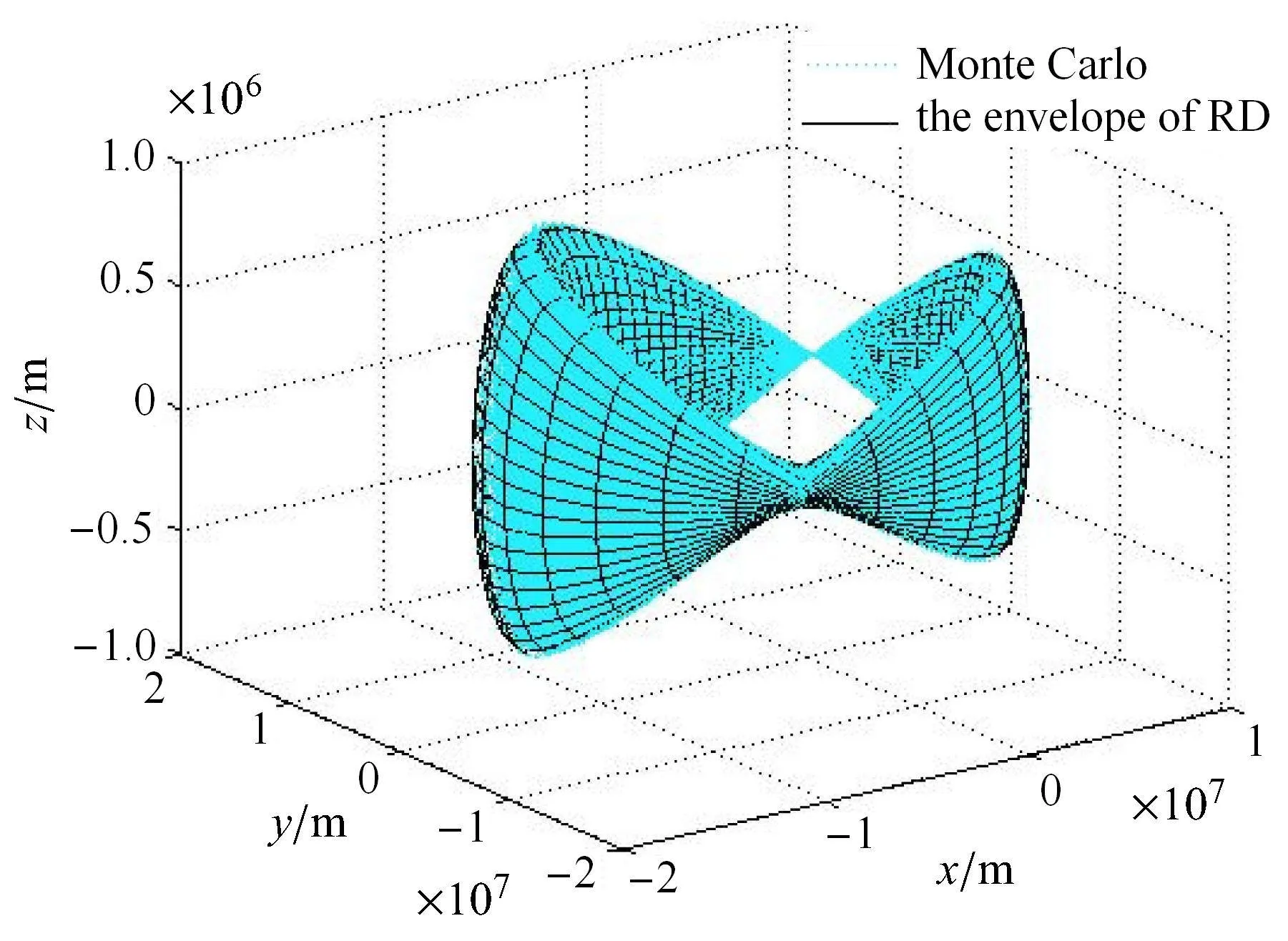
图15 已有算法一仿真结果Fig.15 Results for existing algorithm 1

图16 已有算法二仿真结果Fig.16 Results for existing algorithm 2

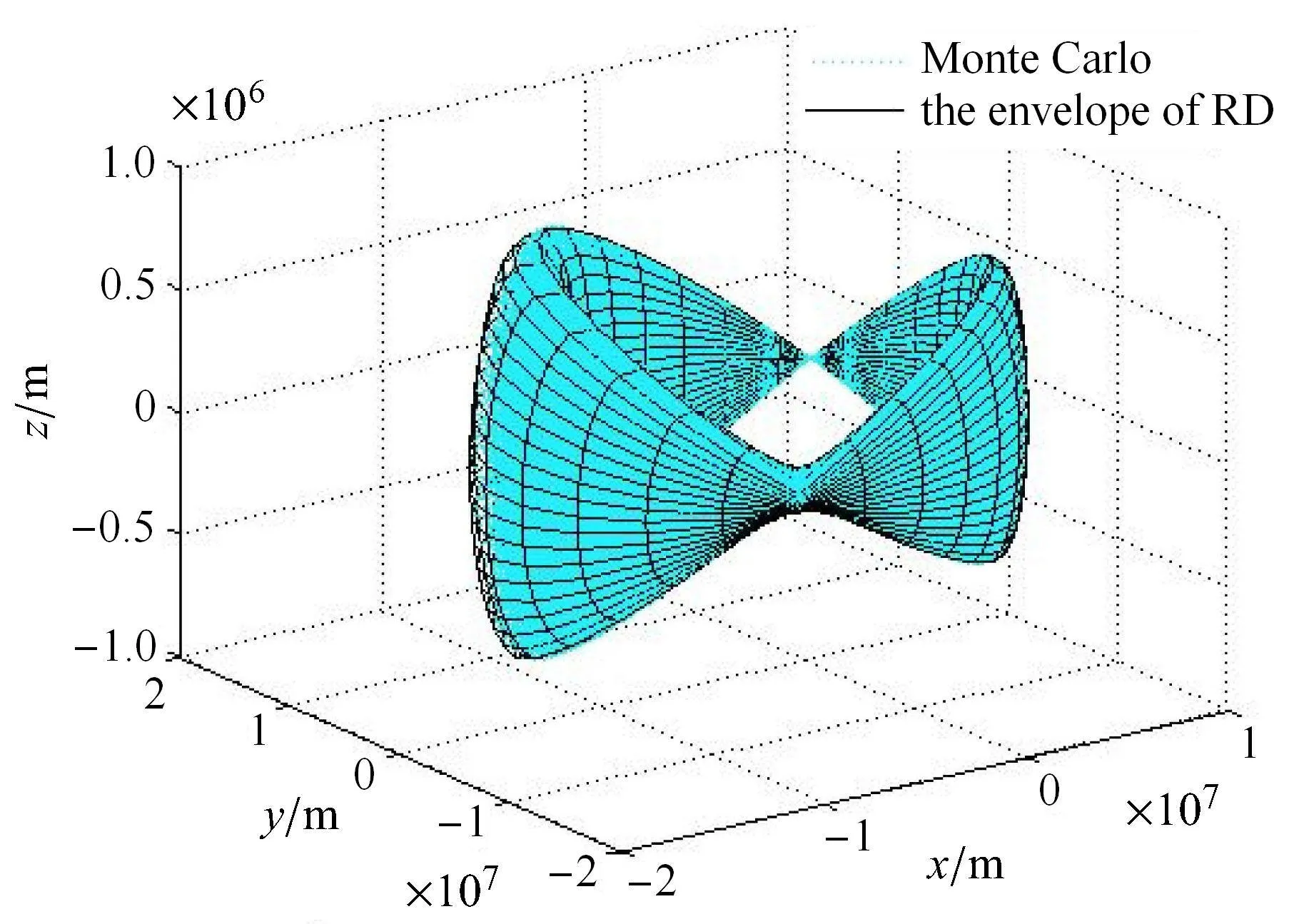
图17 本文算法仿真结果Fig.17 Results for the algorithm of this paper

对比图15 ∼图17 可知，算法一与本文算法求得的结果拟合性较好，基本与随机轨道分布区域贴合，而已有算法二在本章算例给定的初值条件下，所得结果拟合效果较保守，且离机动点位置越远，拟合效果越差.

为了更清晰直观地分析可达域求解结果，将三维可达域投影到初始轨道面内，得到可达域的二维投影如图18 所示.

对比图18 可知，在XY视图内，已有算法二在俯视图内，依然是在机动位置处拟合效果较好，但离机动位置越远，拟合效果越差，计算结果偏保守.已有算法一与本文算法的拟合效果相近且较好.

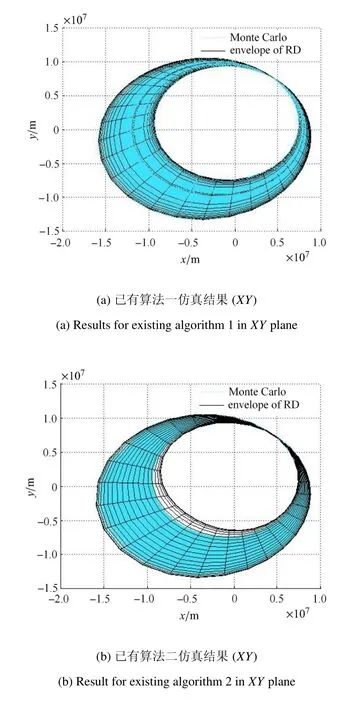
图18 三种算法仿真结果XY 视图Fig.18 Results for three algorithms in XY plane

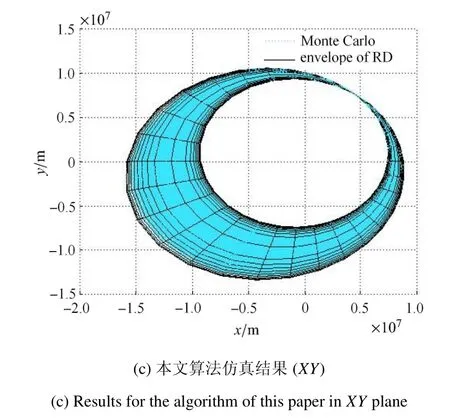
图18 三种算法仿真结果XY 视图(续)Fig.18 Results for three algorithms in XY plane(continued)

4 结论

本文提出了一种精度较高的航天器单脉冲轨道机动可达域求解算法.首先定义了两个角度γ 和ϕ 描述未来终端位置矢量rf的指向，其次提出一种更为简洁的可达性判据判断rf方向可达性，然后通过极值求解算法计算可达位置矢量rf的矢径极值，最后将所有极值点的位置坐标排序汇总即可得到可达域.此外，根据球形机动冲量可达域包络的对称特性，减少了求解流程的计算量.本文算法通过合理选择可达矢径描述参数，简化了终端位置矢量的可达性证明方法并提出可达性判据，将可达域内外包络的求解算法进行了统一，同时将可达域求解问题转化为单一待求参数的非线性方程求解问题，提高了可达域求解的收敛性.最后采用Monte Carlo 仿真验证了所提算法的正确有效性.仿真结果表明：本文所提航天器单脉冲机动可达域求解算法相比已有算法模型更简洁，计算精度更高.