基于统计学的陇东地区沟谷分布及演化研究
2020-12-23赵宽耀李骅锦
袁 爽, 许 强, 赵宽耀, 李骅锦, 王 绚, 周 琪
(成都理工大学 地质灾害防治与地质环境保护国家重点实验室, 四川 成都 610059)
大规模的城镇建设和农业发展带来的沟道侵蚀和水土流失问题日益严重,黄土塬区已支离破碎。黄土高原地质环境本身异常脆弱,近年来一系列重大工程建设(如平山造城、治沟造地、固沟保塬等)其作用速度和强度远超地质营力,对地质环境产生重大影响,并导致灾变不断发生。研究黄土塬区沟谷的分布和发育的规律可以帮助了解黄土沟谷的演化进程,从侧面对黄土地貌的演化分割做出解释,提高人们对黄土地貌演变全过程的认识。研究人类活动驱动下的黄土层内沟谷发育过程及提取沟谷发育量化参数,更是利于人们正确认识自身对黄土沟谷演化的影响,从而达到减缓水土流失和保证生产生活安全的目的。故本文通过对陇东地区沟谷分布和发育规律的统计定量化及可视化表达,得出沟谷间具体的影响程度和发育规律,为固沟保塬工程的实施提供指导。
统计学是通过搜索、整理、分析、描述数据等手段,以达到推断所测对象的本质,甚至预测对象未来的一门综合性科学。统计学用到了大量的数学及其他学科的专业知识,其应用范围几乎覆盖了社会科学和自然科学的各个领域[1],前人运用统计学方法已经对泥石流规模估计[2]、黄土滑坡滑动距离预测等[3-5]方面做了详尽的研究。在黄土高原水系演化方面,学者们也从节理和构造应力场[6]、新构造运动[7]、构造抬升[8-9]和地貌演变等[10]方面做了详尽的研究。在以往的黄土沟谷间发育规律的研究中,前人多从沟谷发育规律与构造的关系[11-12]和沟谷网络发育的模式和速率等[13]方面入手,而随着技术的成熟和发展,通过遥感手段了解土地利用类型对沟谷发育的影响已经成为学者们的一种基础研究手法[14-15]。除此之外,国内外学者还探讨了降雨[16-17]、道路和农业发展[18]、草地固沙[19]、田地与耕作等[20-33]因素对沟谷侵蚀速率的影响,尤其是耕作导致塬边裂隙的产生,加速了沟谷的侵蚀演化[34-35]。研究黄土沟谷的分布与发育规律不能缺少对量化参数的研究,曲率[36-37]、沟壑密度[11]、侵蚀速率[38]都能更好的帮助人们了解沟谷发育的程度。前人虽然已经将统计学方法应用于多个学科的研究,已有学者利用机器学习和统计学方法已经能十分准确的预测泥石流的规模和黄土滑坡的滑动距离[2-5],但很少有人通过统计学方法研究黄土沟谷的分布和发育规律;针对黄土层内沟谷发育的研究,前人从较小的流域尺度研究了田地、草地、道路等用地类型[18-33]和降雨[16-17]对沟谷发育的影响,但对于黄土层内沟谷在耕作条件影响下的演化模式仍缺乏认识;对于黄土沟谷量化参数的研究,前人在沟壑密度、山坡曲率、侵蚀速率等方面[11,36-38]已经研究得十分透彻,但对于较大规模沟谷间分布参数的研究仍不够详尽。
故本文基于野外工作、前人研究和遥感影像的解译,研究构造对沟谷的发育影响关系;通过遥感影像解译陇东地区沟谷的分级情况并将沟谷水系分级;再基于统计检验方法分析沟谷间发育的影响关系;最后,引用安全距离等概念参数量化沟谷发育的规律,旨在为防灾减灾作出贡献,并为黄土沟谷发育、黄土地貌演化及土壤侵蚀研究提供参考依据。
1 研究区概况
研究区位于甘肃省东部庆阳市,习称“陇东地区”。陇东地区地处东经106°20′—108°45′与北纬35°15′—37°10′之间。东接陕西省的宜君、黄陵、富县、甘泉、志丹等县;北邻陕西省吴起、定边及宁夏回族自治区的盐池县;西与宁夏的同心、固原县接壤;南与该省的泾川县及陕西省的长武、彬县、旬邑县相连。南北长207 km,东西跨208 km,总面积27 119 km2。地形北高南低,海拔在885~2 082 m之间,中南部为黄土高原沟壑区,北部为黄土丘陵沟壑区,东部为黄土丘陵区;山、川、塬兼有,沟、峁、梁相间,高原风貌雄浑独特。董志塬面积约为910 km2,平均海拔1 421 m,平畴沃野,一望无垠,是世界上面积最大,土层最厚,保存最完整的黄土塬面,堪称“天下黄土第一塬”。地处东南部的子午岭,林木茂密,水草丰盛其3.13×105hm2次生林,为植被最好的水源涵养林,有“天然水库”之美誉。境内有马莲河、蒲河、洪河、四郎河、葫芦河5条河流,较大的支流有27条。年平均总流量为26.7 m3/s,总径流量8.43×108m3。全市地下水静储量约4.34×109m3,动储量3.71×107m3。全年降水量502.6~985.1 mm,全年平均气温8.8~10.9 ℃,全年全市日照时数2 108.4~2 521.5 h。
2 材料与方法
本文使用ArcGIS 10.3软件基于2009年10月17日至2018年7月26日的3.88 m分辨率Google拼接遥感影像目视解译陇东地区3条流域沟谷的分级情况并将沟谷水系按照所属关系分为主沟、一级支沟、二级支沟和三级支沟。
然后,本文提出一种“正交偏差弧度值”的概念来研究沟谷间的正交关系,从影像上获取的最直接的信息就是沟谷的走向,为了凸显沟谷是存在影响关系的,本文对沟谷的走向做了以下的处理(见图1):先令主沟正交方向的左侧为负,右侧为正,将一级支沟的走向减去其主沟的正交方向得到正交偏差值θ,θ的范围在±90°之间,然后对其除以2π,得到正交偏差弧度值ε。对二级支沟的处理同理。
(1)
式中:ε为正交偏差弧度值;θ为正交偏差值,θ的范围在±90°之间;α为一级支沟(二级支沟)的走向;β为主沟(一级支沟)正交方向走向。
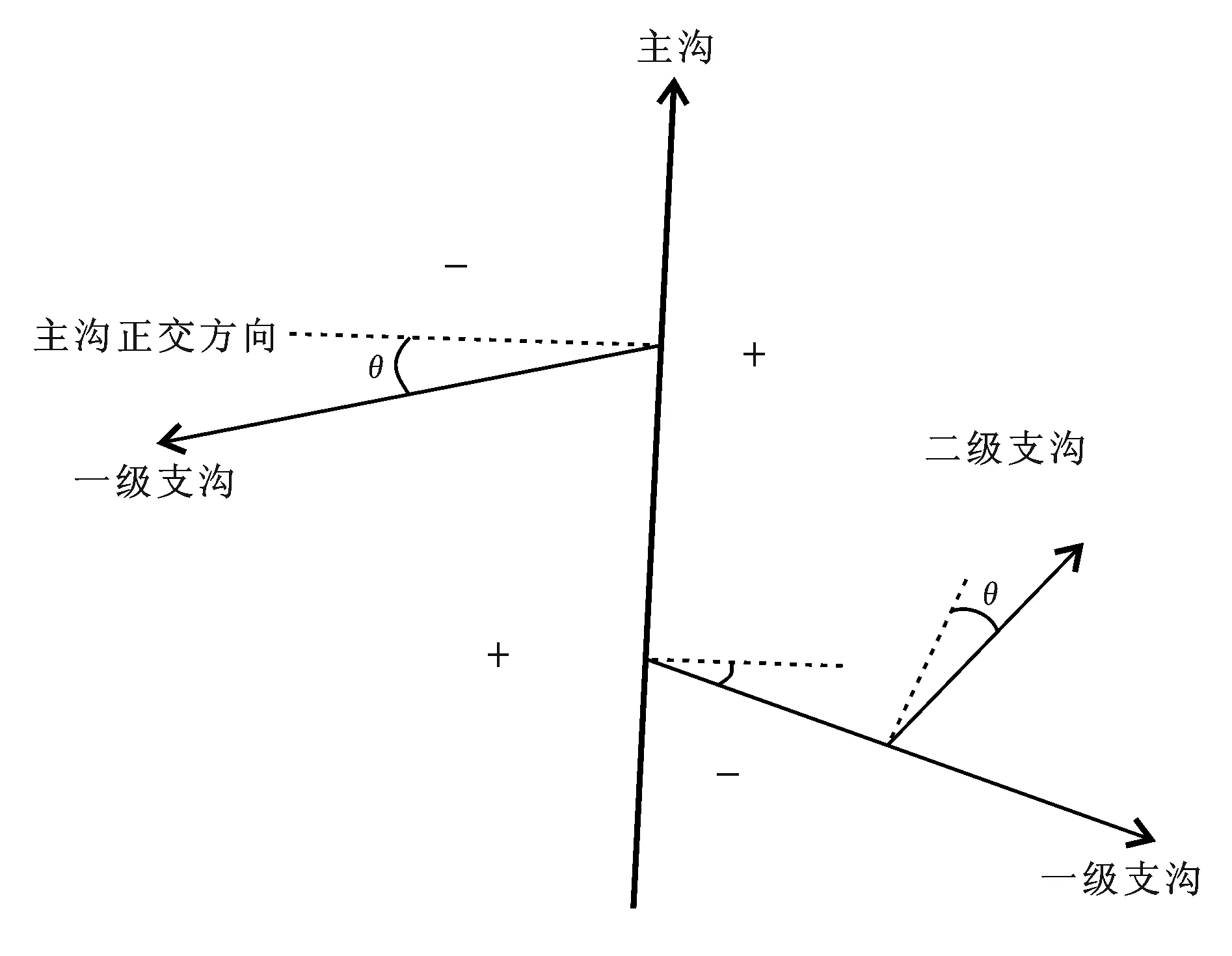
图1 沟谷走向参数处理
对于非随机分布的沟谷走向数据,检验其是否符合正态(常态)性是必要的,而对于大样本的数据统计检验,K-S检验和A-D检验是常用的也是更好的选择。故本文基于Matlab R2018 b软件利用统计学K-S检验和A-D检验来验证数据的连续性和正态性,而满足正态分布的数据则通过“3σ原则”来得到正交偏差弧度值的具体概率分布。
Kolmogorov-Smirnov检验(K-S检验)是比较一个频率分布F(x)与理论分布Fn(x)或者两个观测值分布的检验方法。其原假设H0:两个数据分布一致或者数据符合理论分布。当实际观测值Dn>Dn(n,α)则拒绝H0,否则则接受H0假设。对于一个样本集的累计分布函数Fn(x)和一个假设的理论分布F(x),Kolmogorov-Smirnov statistic定义为:
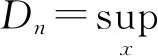
(2)
(3)
式中:I│-∞,x│为indicator function(指示函数):
(4)
Anderson-Darling检验(A-D检验)是将样本数据的经验累积分布函数与假设数据呈正态分布时期望的分布进行比较。如果实测差异足够大,该检验将否定总体呈正态分布的原假设。A2和P-value表述数据正态分布程度,A2值越小,P-value越大,则代表实际的分配和理论分配的差异越小,数据越符合正态分布。
度量假设分布F(x)与经验累积分布Fn(x)之间的距离:
(5)
是权函数:
w(x)={F(x)〔1-F(x)〕}-1
(6)
A-D检验:
{ln〔F(Xi)〕+ln〔1-F(Xn+1-i)〕}
(7)
正态分布(normal distribution),也称“常态分布”,又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。若随机变量X服从一个位置参数为μ,尺度参数为σ的概率分布,且其概率密度函数为:
(8)
则这个随机变量就称为正态随机变量,正态随机变量服从的分布就称为正态分布,记作X~N(μ,σ2)。
最后,本文引用沟间距、纵降比等概念参数量化沟谷发育的规律,为地貌演化进程的重现和预测做出贡献。
3 结果与分析
3.1 各级沟谷发育现状及分布关系
以陇东地区董志塬东侧的马莲河为例,主体河流已经切穿黄土层,下切至基岩层,尚且不能判定河流是在黄土堆积之前就形成的,还是在黄土堆积之后不断下切形成的。但这种现象在陇东地区主要的沟谷水系普遍存在,主要水系的形成可能与构造运动有关。
姜琳等[6]研究发现鄂尔多斯盆地东南部中生代地层中发育有6组节理并且构成3期的正交节理系统(E-W与N-S,ENE-WSW与NNW-SSE,WNW-ESE与NNE-SSW),这与陇东地区主要沟道的走向大致相同。而据白占国[40]研究,黄土沟谷系统空间格局与区域新构造应力场基本吻合,陇东地区新构造主压应力方向为NE 47°~61°,则进一步指明陇东主要沟谷的形成与构造有关。陇东地区主要沟道共16条(见图2),其中近0°~90°走向的沟道有6条,近40°~310°走向的沟道有7条,近70°~340°走向的沟道有3条。
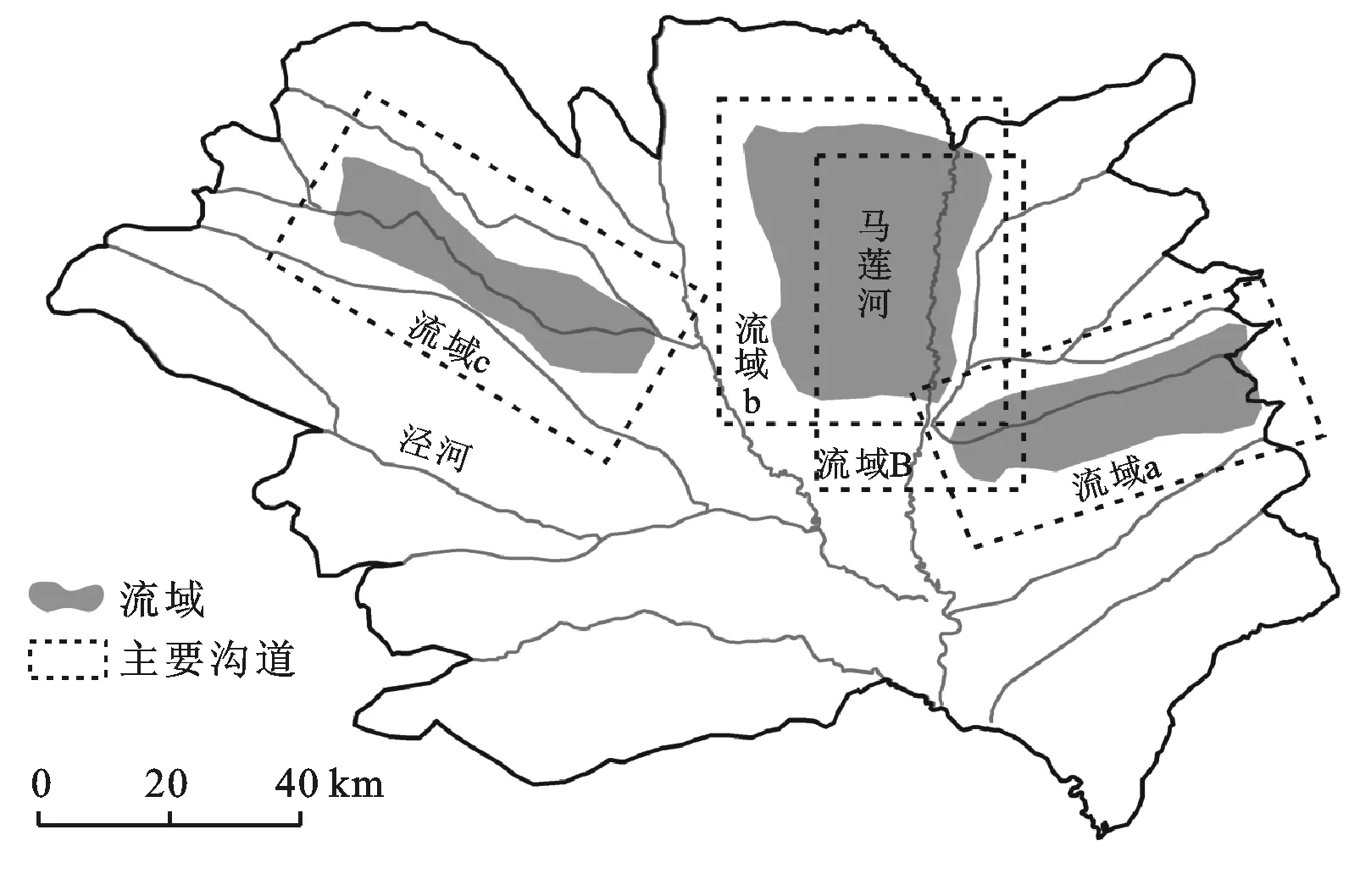
图2 陇东地区主要沟道及研究流域
此外,作者在马莲河流域观测到许多节理的走向与河流的走向近似正交(见图3—4)。而从遥感影像上来看,主沟与支沟呈现近似正交的关系,节理的走向与支沟的走向大致相同(见图2流域B及图3)。这说明主沟与支沟的正交关系类似于正交节理,是受构造控制的。国内外学者也认为支沟的发育与主沟的横断面发育密切相关[11],河谷是平行且间隔规律的构造线[12]。据此本文认为,构造对沟谷的发育起一定的控制作用。
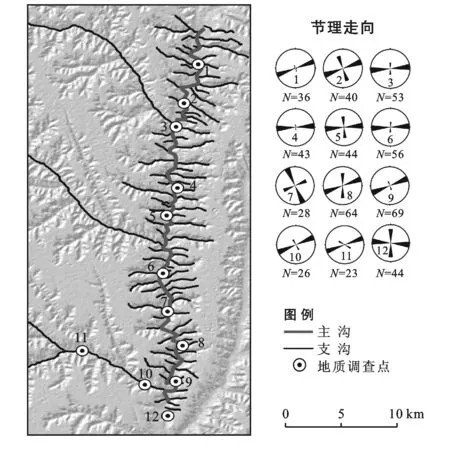
注:左图中地质调查点序号与右图节理走向序号对应,N表示沟数。

注:节理位置见图3地质调查点。a对应序号2;b对应序号5;c对应序号7;d对应序号10;e对应序号12。
3.2 沟谷对下一级沟谷的影响关系
本文首先在陇东地区选取主沟走向不同的3个流域(见图2流域a,b,c)作为研究对象,其中第一个流域位于陇东地区东部,走向NEE-SWW,主沟分为较长的①沟和较短的②沟(见图5a);第2个流域是马莲河流域,位于陇东地区中部,走向近N-S(见图5b);第3个流域位于陇东地区西部,走向NWW-SEE(见图5c)。其次,为了研究主沟是如何影响其一级支沟发育的,本文结合沟谷间的发育关系,将沟谷分为主沟、一级支沟和二级支沟。为了研究一级支沟是如何影响其二级支沟发育的,本文又选取马莲河流域作为研究对象,将两个小流域(图6中①流域和②流域)的沟谷分为主沟、一级支沟、二级支沟和三级支沟(见图6)。
统计学是通过搜索、整理、分析、描述数据等手段,以达到推断所测对象的本质,甚至预测对象未来的一门综合性科学。对于沟谷间发育的研究,考虑到沟谷的走向并是一个大样本的随机分布,它是存在客观规律的,而统计学检验可以通过对数据的整理分析得到这个客观规律。本文对3个流域沟谷的正交偏差弧度值进行统计分析,得到了4组一级支沟对主沟的正交偏差弧度值数据和2组二级支沟对一级支沟的正交偏差弧度值数据。对于数据的处理方法,本文基于Matlab R2018 b软件参照前人研究[2]先对6组数据进行K-S检验(Kolmogorov-Smirnov检验)来检验数据的连续性,然后满足K-S检验的数据进行A-D检验(Anderson-Darling检验)来检验数据的正态性。
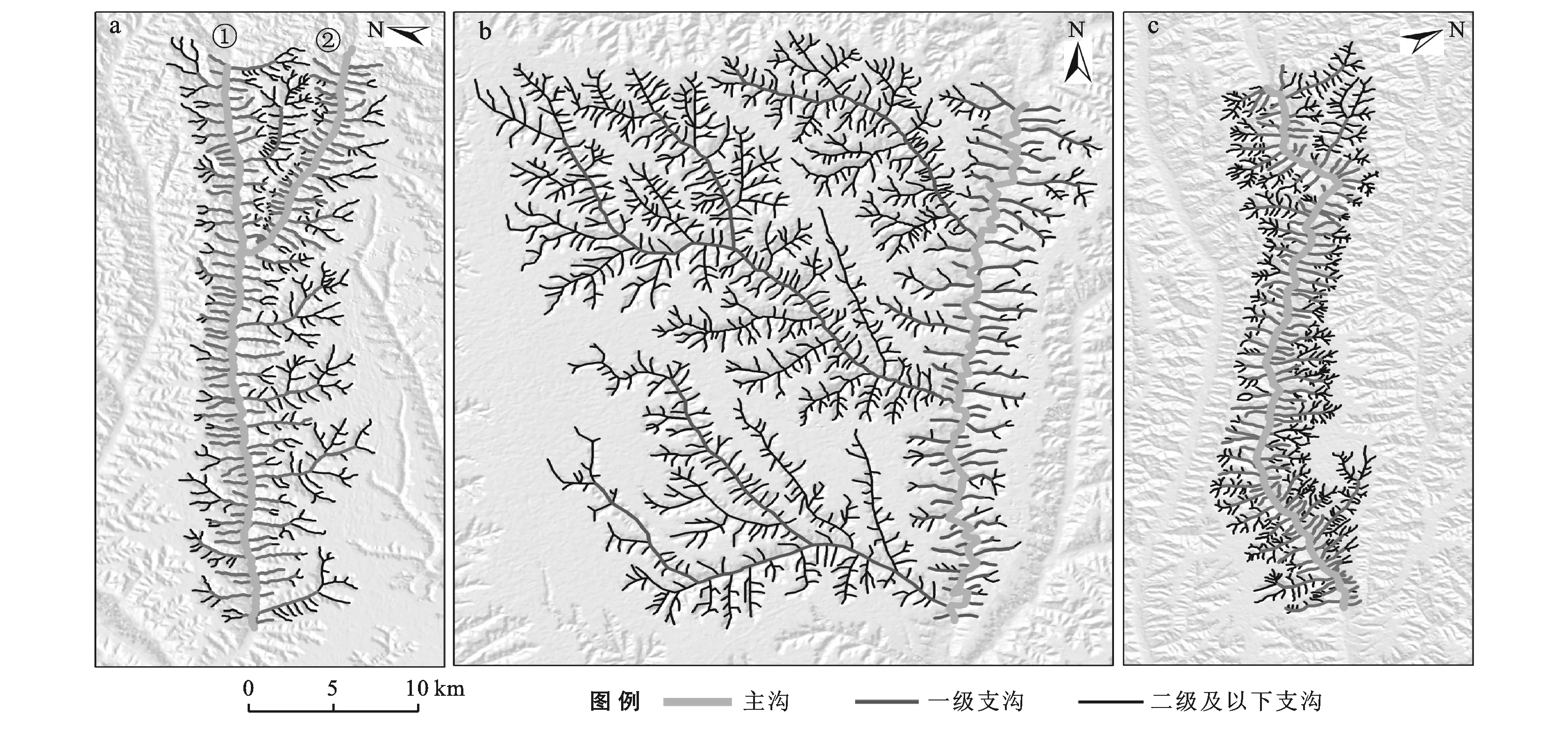
图5 3个典型流域主沟与一级支沟的分布

图6 二流域一级支沟与二级支沟的分布
K-S检验是比较频率分布与理论分布的检验方法,对于一组数据先提出假设H,即假设该组数据连续,当H=0时,表示接受该假设,数据连续;当H=1时,表示拒绝该假设,数据不连续。检验结果显示:6组数据的假设H结果均为0,6组数据均满足连续性(见表1)。A-D检验是将样本数据的经验累积分布函数与假设数据呈正态分布时期望的分布进行比较,目的是检验数据的正态性。A2和P-value表述数据正态分布程度,A2值越小,P-value越大,则代表实际的分配和理论分配的差异越小,数据越符合正态分布,即当A2值较小,且P-value >0.05时,可认为其符合正态分布。

表1 3个典型流域K-S检验结果
本文选取了5种正态函数分布(普通函数、极值函数、对数函数、指数函数和韦布尔函数)去拟合数据的正态性,发现多组数据对normal函数的符合性较好,且都符合正态分布(见表2)。
结合K-S和A-D检验的结果,本文认为4组一级支沟对主沟的正交偏差弧度值数据和2组二级支沟对一级支沟的正交偏差弧度值数据均符合正态分布。
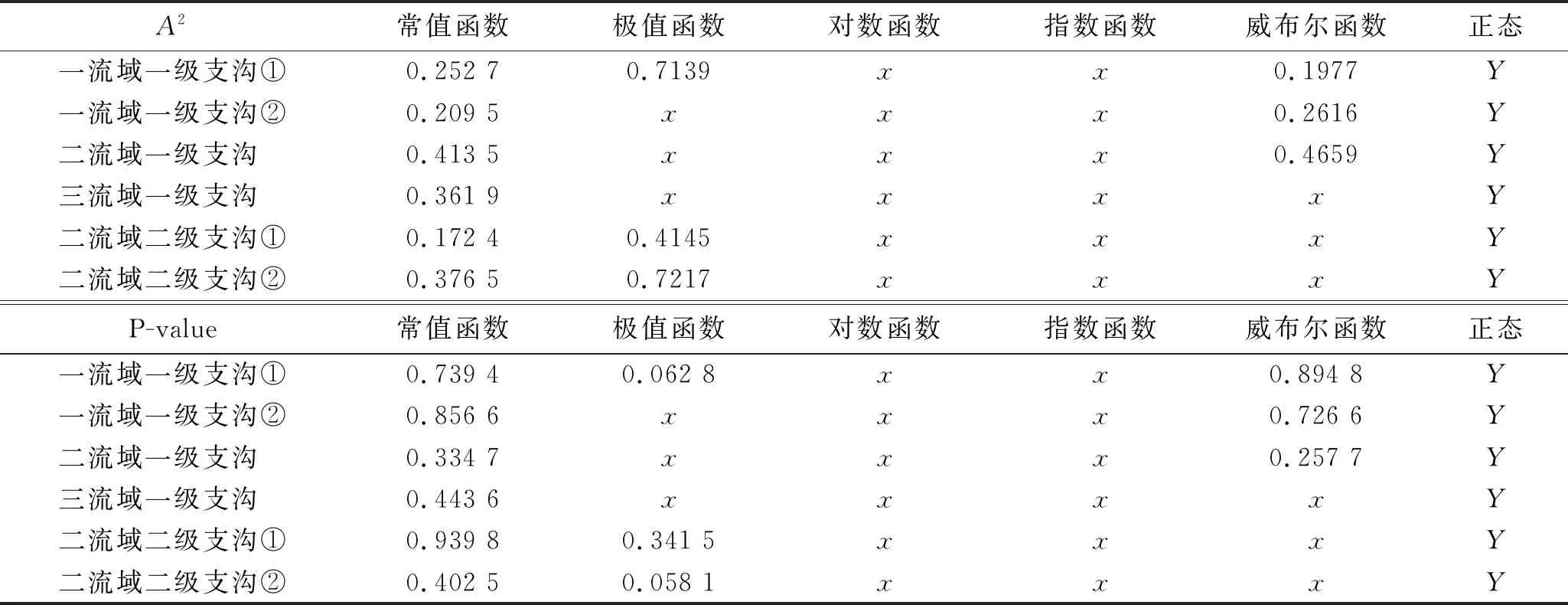
表2 3个典型流域A-D检验结果
3.3 各级沟谷演化分析
正态分布的形状是一条钟形曲线,中间高,两边低,关于x=mean(均值)对称。正态分布有一个性质“3σ原则”,也就是在95%的置信率下,在距离均值1倍标准差(Std)的时候,其概率分布为68.3%;2倍标准差的时候概率分布为95.4%;3倍标准差的时候概率分布为99.7%。对于本文研究来说,相当于有68.3%的正交偏差弧度值落在了±1倍标准差的区间内,95.4%的值落在了±2倍标准差的区间内,99.7%的值落在了±3倍标准差的区间内(见表3)。

表3 正交偏差弧度值的正态性分布
在统计学中,80%的概率称为统计学显著。但是“3σ原则”所表现出的概率分布要么过小要么过大,不能很好的体现正交偏差弧度值的分布规律。所以,本文通过查表求得,当概率为80%时,为距离均值1.281倍标准差。
那么有理由相信,一级支沟的走向是落在其主沟正交方向±1.281倍标准差的区间内的。本文在6组正交偏差弧度值数据的支撑下认为:在忽略均值大小的情况下(6组数据均值都较小,均未超过8.2°),3个流域的一级支沟分别是向其主沟正交方向±20.1°,±22.4°,±30.1°,±21.2°方向发育的;而二级支沟是向其一级支沟正交方向±34.2°和±19.5°方向发育的(见表4)。换一种说法来讲,在80%的显著概率下,主沟与一级支沟的夹角ω(ω范围在±90°之间)不小于69.9°,67.6°,59.9°和68.8°;一级支沟与二级支沟的夹角ω不小于55.8°和70.5°。这充分说明了主沟与一级支沟、一级支沟与二级支沟在统计学上是存在发育上的联系的,70°可视为沟谷发育夹角的极限值。
本文根据构造影响和沟谷统计检验以及沟谷正态分布性质综合分析沟谷演化的始末。演化伊始,主沟在构造应力的影响下不断扩张形成与现今大致相同的分布情况(见图7a),部分受构造控制的一级支沟开始沿与主沟近似垂直的方向扩张发育,这类一级支沟延申较长,此时水系网络构建了雏形;而后,黄土堆积和侵蚀并行,大量一级支沟渐渐沿与主沟近似垂直的方向扩张发育,但延申较短(见图7b),与此同时原先受构造控制发育的一级支沟继续侵蚀延申,并发育出大量树杈状的二级、三级支沟(见图7c);最后,随着侵蚀不断加剧,沟壑蔓延,最终形成了见图7d所示的沟谷现状。

表4 80%概率分布下的θ取值

图7 沟谷演化过程示意图
4 讨论与结论
4.1 讨 论
本文沟谷分级方法有别于Strahler和Shreve等人的经典河网分级方法,原因有二:首先本文着重于较大规模的沟谷间分布的研究,忽略较小规模的沟谷,而经典河网分级方法则是对所有沟谷进行命名分级,对于本文研究不能突出重点,徒增工作量;其次,Strahler和Shreve等人的经典河网分级方法是从新到老依次分级,而本文研究的是沟谷的演化,需要从老到新分级研究。故分级方法和命名有所不同。
关于黄土高原早期水系的形成时间,雷祥义等[7]认为早期的黄土高原水系由一系列内流水系和湖盆构成,而水系形成的主要动力受第四纪新构造运动及其古气候环境变化的控制。李吉均等[8]潘保田等[9]指出,在1.67×106~1.45×106a间,黄土高原隆升至1 100 m,后续的隆起活动导致流水落差逐渐增大,支流增多,逐渐形成现代黄土高原水系。而从水系发展上来看,六盘山以东河谷阶地一般为5级,黄土开始堆积的时间不早于1.23 Ma BP[7],直到早中更新世末、晚中更新世初黄河一级支流和较大的二级支流形成了较完整的水系。然而,马莲河是泾河最大支流,并且长于泾河正源,汉以前曾作为泾河干流上游。泾河是黄河第一大支流渭河的第一大支流。也可认为马莲河曾是黄河的二级支流。结合前人研究及《中国14C年代学研究》中对第四纪地层年代的分析,本文认为黄土开始堆积的时间和马莲河的形成时间相差无几。
在许多情况下,河谷是位于平行和规则间隔上的构造线[12],说明沟谷的发育规律是有迹可循的。本文统计了3个流域一级支沟和二级支沟的沟间距和纵降比,研究发现:4条一级支沟的沟间距几乎相同。在50%的概率范围内,一级支沟的沟间距为0.6~1.0 km,二级支沟的沟间距为0.4~0.7 km,一级支沟的沟间距总体上大于二级支沟;而在80%的概率范围内,一级支沟的沟间距为0.4~1.3 km,二级支沟的沟间距为0.3~1.0 km,二者相差无几(见图8)。本文认为,沟间距可以作为一种安全距离的指标,比如:当一条二级支沟侵入到人类活动范围内时,其两侧1 km范围内是不应耕种农田的。除了沟间距之外,坡度也被视为影响沟谷演化的重要因素[39],但一条沟谷的坡度是不固定的,故本文通过沟谷总体的纵降比(比降)来研究“坡度”的影响:除一流域一级支沟b外,其他几条一级支沟的纵降比大致相同。而事实上,一流域一级支沟b是一条很小的沟,统计样本量较少,误差率高,可以忽略(见图9)。从总体上看,一级支沟的纵降比是小于二级支沟的。
本文期望以后的研究能通过对多类参数(沟间距、纵降比等)的模拟和数据的运算,可以得到某个塬区被沟谷蚕食的演化全过程,也可以预测该塬区被进一步蚕食甚至消失的时间。
4.2 结 论
本文通过遥感影像解译陇东地区三条流域沟谷的分级情况并将沟谷水系按照所属关系分为主沟、一级支沟、二级支沟和三级支沟;再基于统计检验方法分析主沟与一级支沟、一级支沟与二级支沟的正交偏差弧度值,得到了沟谷间发育存在近似正交影响关系;最后引用安全距离等概念参数量化沟谷发育的规律,重现和预测地貌演化的进程。
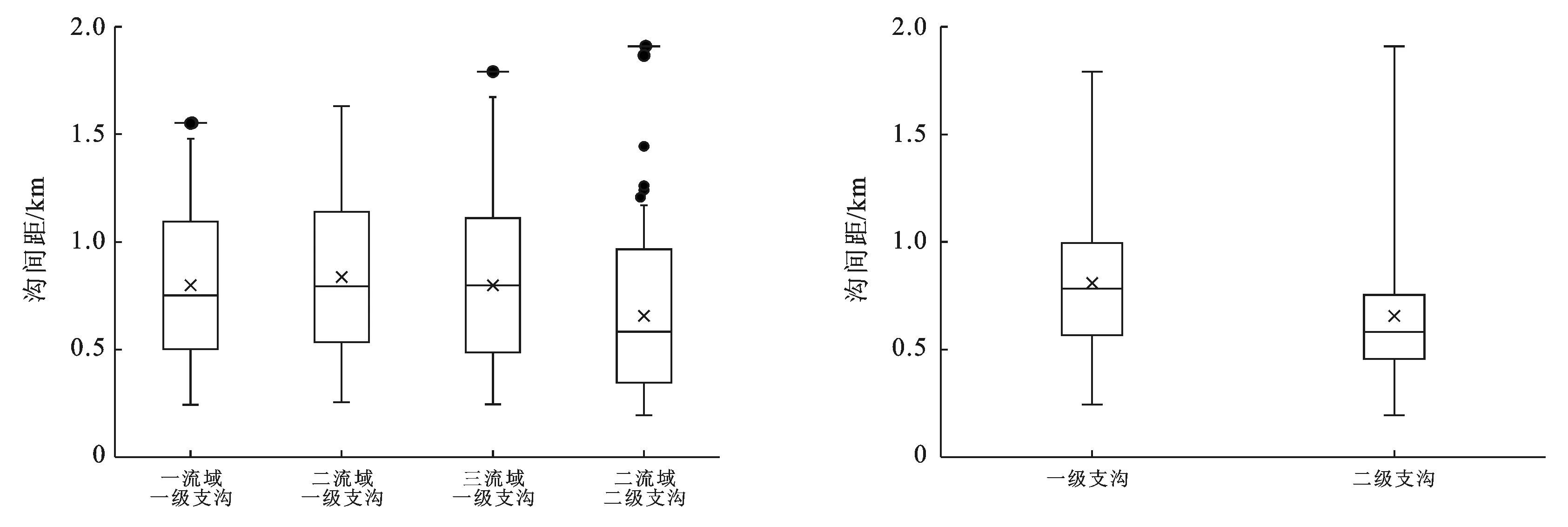
图8 陇东地区3条典型沟谷沟间距箱线图
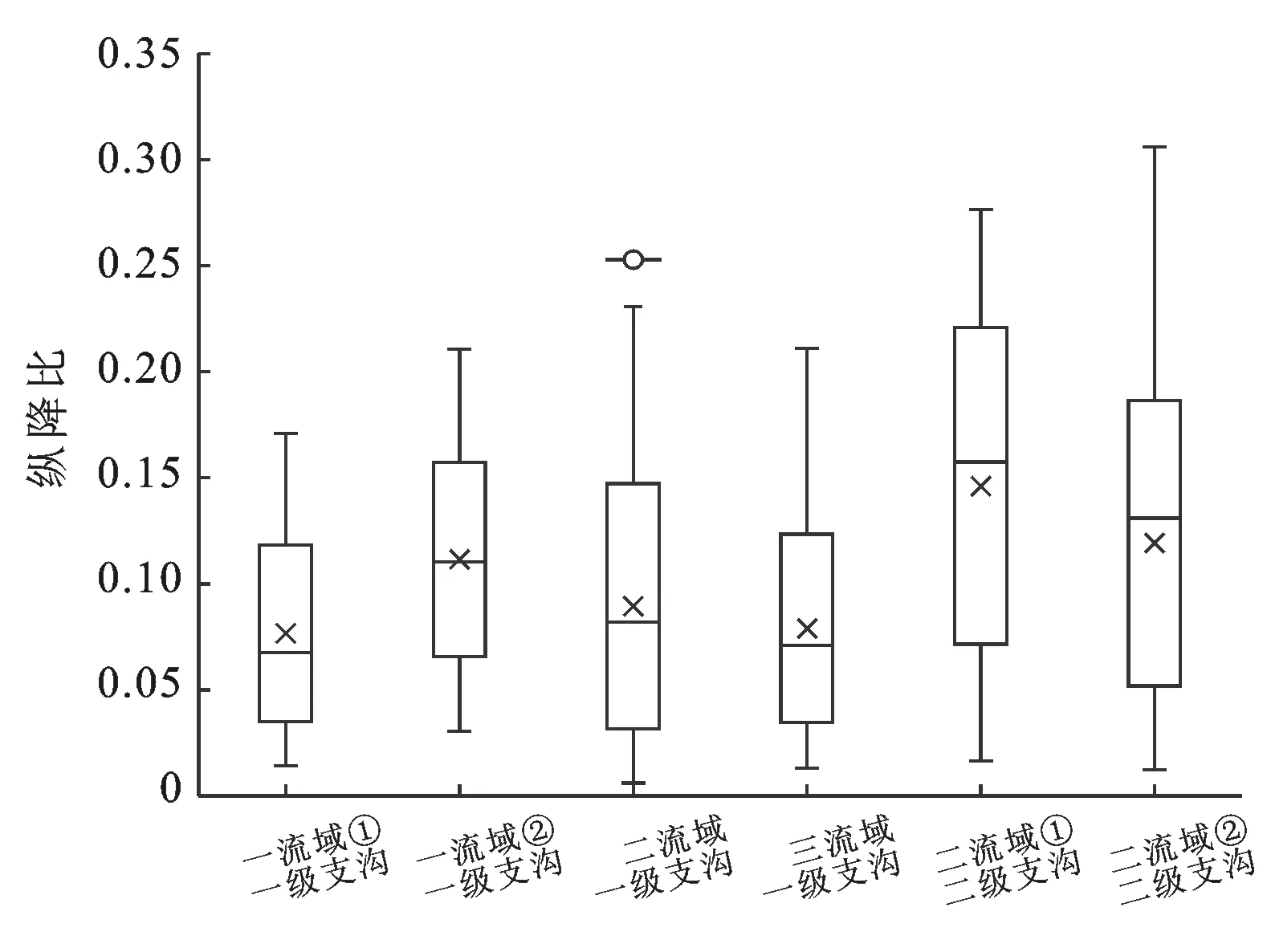
图9 陇东地区3条典型沟谷纵降比箱线图
(1) 基于遥感解译和前人研究发现,主沟与支沟呈现近似正交的关系,节理的走向与支沟的走向大致相同,构造对沟谷的发育起一定的控制作用。
(2) 基于统计检验发现,4组一级支沟对主沟的正交偏差弧度值数据和2组二级支沟对一级支沟的正交偏差弧度值数据均符合正态分布。
(3) 在80%的显著概率下,主沟与一级支沟的夹角不小于69.9°,67.6°,59.9°和68.8°;一级支沟与二级支沟的夹角不小于55.8°和70.5°。主沟与一级支沟、一级支沟与二级支沟在统计学上是存在发育上的联系的,70°可视为沟谷发育夹角的极限值。
(4) 在50%的概率范围内,一级支沟的沟间距总体上大于二级支沟;在80%的概率范围内,二者相差无几。沟间距可以作为一种安全距离的指标;一级支沟的纵降比总体上小于二级支沟。
