针齿壳成形磨削砂轮廓形修整

2020-12-23胡晨辉邓效忠苏建新柯庆勋

河南科技大学学报(自然科学版) 2020年2期

胡晨辉，邓效忠，b ，苏建新，b，柯庆勋

(河南科技大学 a.机电工程学院;b.机械装备先进制造河南省协同创新中心，河南洛阳 471003)

0 引言

旋转矢量(rotate vector,RV)减速器因具有传动比大、传动效率高、承载能力强、结构紧凑和回转误差小等优点，被广泛应用在机械传动领域中[1-3]。针齿壳的加工精度和加工效率影响了RV减速器的工作精度和生产成本。因此，高精度针齿壳的生产制造是突破RV减速器生产技术的关键步骤之一。文献[4]分析了RV减速器的传动原理、针齿壳的结构特点及材料特性，设计了一种满足针齿壳加工过程中质量控制的工艺方案，大大提高了加工效率。文献[5]根据针齿壳内齿结构及插齿加工运动原理，求解出了插齿刀的理论齿形方程，总结了插齿刀齿形设计方法及刀具相关参数的选择原则。文献[6-7]对展成法加工针齿壳进行了研究，运用展成法加工针齿销孔，给出圆弧干涉对径向进给顶切、插刀圆弧齿中心圆半径的影响规律。文献[8]根据内齿轮与成形砂轮的运动关系，以直线逼近渐开线的方法，对内齿轮成形磨削的砂轮修整进行了研究，提高了磨削精度。上述文献中多以展成插齿法加工针齿壳，虽一定程度上提高了针齿槽加工效率，但在精度方面无法适应高精密RV减速器的使用要求。关于成形磨削加工针齿壳方面的研究较少，因此本文采用成形法磨削针齿壳。由于针齿壳尺寸限制，当加工大传动比的针齿壳时，需要磨削的针齿槽较多，若选用普通刚玉砂轮则容易造成砂轮磨损，因此应选用立方氮化硼(cubic boron nitride,CBN)砂轮[9]。依据成形磨削理论[10]，运用CBN砂轮对针齿壳中针齿槽的成形磨削及砂轮修整技术进行了研究，运用MATLAB数值仿真模拟并求解出成形砂轮廓形修整的相关运动参数,通过砂轮修整试验验证了理论的可行性。

1 针齿壳成形磨削砂轮修整

1.1 针齿壳成形磨削数学模型的建立

某型号RV减速器针齿壳内曲线如图1所示，半圆形针齿槽在针齿壳内圈均匀分布，针齿槽的成形磨削是用砂轮架把成形砂轮送入针齿壳内圈进行磨削。砂轮除了沿自身轴线旋转外，还沿工件轴线方向往复运动，工件随工作台做进给运动，如此往复运动完成整个针齿壳的加工。因此，首先需要建立针齿槽廓形方程。

图1 某型号RV减速器针齿壳内曲线

以针齿壳中心O为原点，建立如图1所示的二维坐标系，Rb为针齿壳内径，Rb一般略小于或等于针齿分布圆半径Rz，这样针齿至少有1/2包容在针齿壳中。M为针齿槽廓形上一点，O1为针齿槽中心点，θ为O1M与Y轴正方向的夹角。针齿槽廓形方程可表示为：

(1)

其中：rz为针齿半径,mm;Rz为针齿分布圆半径,mm;θ为角参量,rad。

1.2 针齿壳成形磨削砂轮廓形求解

洛阳某数控机床有限公司开发的针齿壳复合成形磨削机床，如图2所示，该磨削机床有3个直线轴(X，Y，Z)，2个旋转轴(1个回转台旋转轴B1，1个砂轮旋转轴B2)，可通过一次装夹完成对针齿槽、内圆及端面的磨削。成形砂轮廓形修整精度直接对磨削齿形精度产生影响[11]。根据成形磨削过程中砂轮与针齿壳的相对运动及位置关系，建立针齿槽成形磨削坐标系，如图3所示。

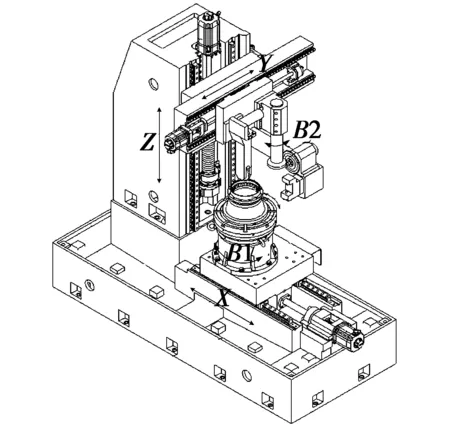
图2 针齿壳复合成形磨削机床

图3 针齿槽成形磨削坐标系

图3中，O1-X1Y1Z1为工件中心坐标系(即针齿壳坐标系)，Og-XgYgZg为砂轮中心所在坐标系，p为针齿壳中心与砂轮中心的距离，p=Rz+rz-Rg，其中:rz为针齿半径,mm;Rz为针齿分布圆半径,mm;Rg为成形砂轮半径,mm。针齿槽对称线与砂轮轴向截形的对称线重合，则针齿槽齿面矢量方程可表示为：

(2)

其中：z1为针齿槽齿廓宽度，mm。

设砂轮坐标系点坐标矢量方程为：

(3)

由针齿壳坐标系到砂轮坐标系的坐标转换矩阵为Mg1，经坐标转换后：

rg=Mg1r1,

(4)

其中，转换矩阵为：

(5)

则在Og-XgYg平面内砂轮轴向廓形坐标方程可表示为：

(6)

将轴向廓形上的点绕Xg轴旋转可得到砂轮回转面上的点矢。

2 金刚石滚轮轨迹的仿真计算及试验

图4 金刚石滚轮修整砂轮示意图

2.1 金刚石滚轮轨迹计算

本文采用控制金刚石滚轮与被修整砂轮之间的双轴联动，实现金刚石滚轮与砂轮对磨，完成砂轮修整。该方法结构简单、金刚石滚轮耐用度高，能修整出形状较为复杂的砂轮廓形[12-13]。金刚石滚轮利用半径为R的圆弧来修整砂轮，如图4所示。

金刚石滚轮的轨迹即砂轮廓形的外等距曲线[14]。根据微分几何学[15]可知：

rR=rg+Rn，

(7)

其中：rR为砂轮外等距曲线上的矢量；rg为砂轮廓形点的矢量；R为金刚石滚轮半径;n为修形后砂轮廓形的单位法矢量。

n=k×t，

(8)

其中：k为z轴单位法矢量；t为z轴单位切矢量。

(9)

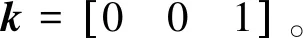
(10)

将式(4)和式(7)代入式(8)，可得金刚石修整轮的中心轨迹方程：

(11)

图5 程序编写流程图

2.2 金刚石滚轮轨迹数值仿真

为了便于成形磨削过程中砂轮修整参数的计算和保存，运用MATLAB软件进行针齿壳成形磨削砂轮修形及数值仿真。根据摆线轮与针齿壳的设计参数，实现不同型号针齿壳成形磨削砂轮的廓形求解及相应金刚石修整轮的修形轨迹仿真，程序编写流程如图5所示。首先，确定针齿壳的基本参数,并判断是否需要抽齿(当传动比较大，要求的针齿数较多时，为避免针齿壳强度削弱，需间隔性地抽去1个或2个针齿)，并由齿廓精度值求解出针齿槽廓形的离散点坐标值，用于砂轮廓形与金刚石滚轮运动轨迹的计算及砂轮修整程序输出。

本文所要加工的某型号针齿壳相关参数如表1所示。

表1 某型号针齿壳相关参数

根据输入的参数可计算短幅系数、针轮基圆半径等其他参数，判断是否需要进行抽齿，并绘制针齿壳廓形、内曲线及金刚石滚轮修整轨迹曲线。图6为针齿壳内曲线，是把针齿壳相关参数输入砂轮修整软件并运行得到齿面离散点坐标，再由齿面离散点坐标生成的曲线。图7为金刚石滚轮运动轨迹。图7中，蓝色曲线为金刚石滚轮圆弧中心运动轨迹，黑色曲线为所修整的砂轮廓形，通过金刚石滚轮轴与砂轮轴的插补联动完成砂轮廓形的修整。

图6 针齿壳内曲线

图7 金刚石滚轮运动轨迹

2.3 砂轮修整试验和磨削试验

为了验证理论计算的结果，在洛阳科大越格数控机床厂生产的针齿壳复合成形磨齿机(YK7350NF)上进行了相应的砂轮修整试验及磨削试验，。砂轮修整试验如图8所示，成形砂轮与金刚石滚轮通过两轴联动完成砂轮的修整。砂轮修整后，通过砂轮架上下移动、工作台转动完成针齿壳的磨削过程，如图9a所示，磨削出的针齿壳成品如图9b所示。

图8 砂轮修整试验图9 磨削试验

用修整出的成形砂轮磨削针齿壳,将磨削的针齿壳放在齿轮测量中心检测，扫描出齿面点坐标。表2为针齿廓形的检测扫描点，通过比较实际检测齿面点坐标与理论齿面点坐标发现，齿廓形状X值最大绝对误差为0.032 02 mm,最小绝对误差为0.005 63 mm;Y值最大绝对误差为0.031 30 mm，最小绝对误差为0.001 85 mm，是由机床相对位置误差和工件偏心导致的，但总体误差较小，验证了砂轮修整理论的正确性。