不同负载下的电机温度场计算

吴尧辉，方 鑫

(河南理工大学 电气工程及其自动化学院，焦作 454150)

0 引 言

电机的温升计算对电机安全及稳定运行都极为重要。电机的温升会使绕组的物理、电气及力学性能发生变化，当温升达到一定限度时，破坏绕组绝缘，导致电机出现匝间短路、相间短路等故障，同时构成电机的金属件的强度和硬度也会随温度的升高而逐渐下降。

电机温升不仅受到外界因素影响，还跟自身结构等因素有关，文献[1]指出，外界条件对电机温升的影响，主要包括环境温度和海拔高度对电机温升的影响。文献[2]分析了电机在2～4倍过载情况下的温升情况，通过对比发现，永磁轮毂电机在运行中复杂，齿部和轭部越大，磁通饱和现象越严重，严重影响了电机的正常运行。文献[3]针对轮毂电机的热负荷大和温升显著问题，采用磁热双向耦合的方法，准确地计算了电机损耗和温升数值。文献[4]基于有限元法对电机三维全域稳态温度场进行了计算，发现电机转子导条与端环的连接处的热流密度值较大，说明此位置极易发生断裂故障这一结论与实际电机情况相符。

由于电机的温升计算涉及到多物理场,导致计算复杂，目前常用的计算方法有热网络法[5-6]、有限元法[7-8]。其中热网络法将电机各部分等效为热阻连接成热网络来计算温升；有限元法则是将电机的各个部分划为一定数量的网格，在网格内用现代数值求解方法构建方程进行电机温升计算。就求解精度和时长对比来看，有限元精度更高,但是时间较长;由于热网络法求解快,且具有一定的精度。考虑到以上因素,本文采用热网络法来计算电机温度场。

1 热网络模型

1.1 模型建立

本文以一封闭式小型鼠笼异步电机为研究对象，电机的主要参数如表1所示，根据参数建立电机的几何模型如图1所示。

表1 主要参数

为了便于计算电机温升，作出如下假设：

1) 电机运行过程中环境温度不变；

2) 不考虑底座、接线盒，电机沿圆周方向对称，圆周方向冷却条件相同；

3) 忽略定转子绕组和导体的集肤效应；

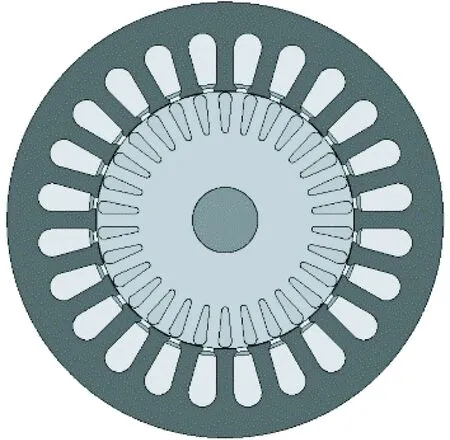
图1 几何模型图

基于以上假设，根据电机的结构将电机划分为机壳、定子铁心、绕组、绕组端部、气隙、转子铁心、导体、端环、转轴、端盖等部分。将每个部件对应的热阻热源连接起来构成整个热网络模型。图2为电机的热网络模型图。

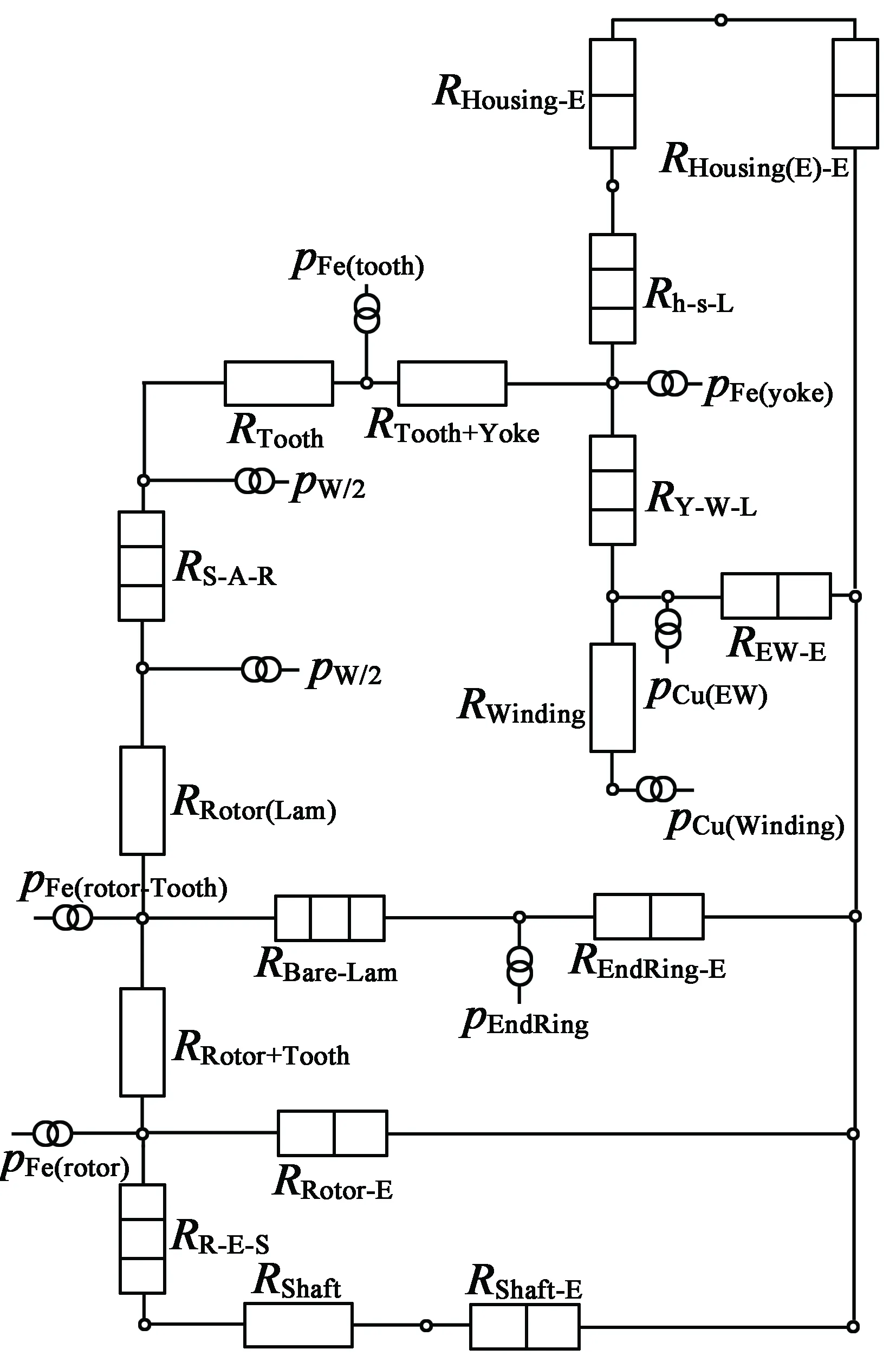
图2 热网络模型节点图

图2中，RHousing-E，RHousing(E)-E为机壳和机壳端部与空气间的热阻；Rh-s-L为机壳与空气及定子铁心间的热阻；pFe(yoke)为定子铁心轭部损耗；RTooth+Yoke为铁心热阻；pFe(tooth)为定子铁心齿部损耗；RTooth为铁心磁部热阻；pW为定子铁心损耗；RS-A-R为定子内表面和转子外表面及气隙间的热阻；RRotor(Lam)为转子齿部外部铁心的热阻；pFe(rotor-Tooth)为转子齿部铁耗；RBare-Lam为导体及转子铁心及空气间的热阻；pEndRing为转子端环损耗；REndRing-E为转子端部与空气间的热阻；RRotor+Tooth为转子齿部内部及转子内部间的热阻；pFe(rotor)为转子铁心损耗；RRotor-E为转子铁心与空气间的热阻；RR-E-S为转子内部与转轴及转子和空气间的热阻；RShaft-E为转轴和空气间的热阻；RY-W-L为定子铁心和绕组及空气间的热阻；pCu(EW)为绕组端部的损耗；pCu(Winding)为绕组的损耗；REW-E为绕组端部和空气间的热阻；RWinding为绕组的热阻。

1.2 电机传热系数计算

热能传递的三种方式分别是热传导、热对流、热辐射。在小型异步电机的温度场计算中,热辐射造成的散热量在电机总散热量中所占比例较小,本文忽略热辐射，只考虑热传导和热对流,对应的导热系数和散热系数计算。

1.2.1 导热系数的计算

对于电机材料的导热系数的计算常以傅里叶导热定律为基础[9]，导热系数的定义如式(1)，电机材料的导热系数如表2所示。

(1)

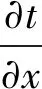
表2 电机材料导热系数

1.2.2 散热系数的计算

1) 端盖和外壳散热系数的计算

本文研究的是封闭自冷式电机，转子端部没有风扇，电机主要通过电机外壳和端盖散热，向周围环境散热。散热系数按下式：

(2)

式中：α0为自热条件下的散热系数；vi为电机内部空气流速；T0为电机外部表面的温度。

2) 端部散热系数的计算

电机端部空间空气的流速取决于多种因素，包括端部绕组的形状和长度、简单风扇和端环晶片所产生的附加扇形效应、转子端部的表面光洁度和湍流，同时考虑海拔高度对散热的影响，因此电机端部这一区域的冷却计算是整个电机最难的部分。通过与端部空间流体接触的表面的对流换热系数与局部流体速度的曲线拟合[10]，如式(3)，本文中电机端部主要参考数据如表3所示。

(3)

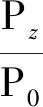
表3 端部散热参考数据

3) 气隙等效传热系数

电机运动时，由于转子旋转，气隙空气受到转子切向运动影响，同时转子端环上的平衡块以及风叶会扰动气流，因此对转子表面换热会有较大影响，引入了流体努塞尔准则确定[11]，利用静止流体的导热系数来描述气隙中流动空气的热交换能力λeff，可按下述方法得出：

(4)

(5)

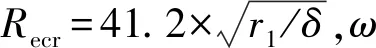
2 损耗计算

2.1 损耗计算

电机损耗主要由铁心损耗、铜耗、机械损耗、杂散损耗组成，对于小型异步电机各部分来说，电机的附加及杂散损耗复杂,不易计算且所占比例较小，常常忽略或者乘以一定的比例系数计算。

电机的铁心损耗主要有基本铁耗和附加损耗组成，采用修正的Steinmetz计算铁耗[7]，如下式：

p=Khf·B(α+βB)+2π2Keddyf2B2

(6)

式中：Kh为磁滞损耗系数；f为基波频率；B为磁密；α,β为磁滞损耗经验系数；Keddy为涡流损耗系数。

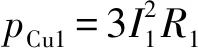
异步电机的机械损耗包括轴承摩擦损耗、转子风摩擦损耗以及通风摩擦损耗。这些损耗在一般情况下都很难以计算，大部分都是根据经验数据以及现有电机实验数据来计算。

2.2 损耗分布

对比分析电机在不同负载下的损耗值，环境温度为28 ℃，具体数值如表4所示，柱状图如图3所示。

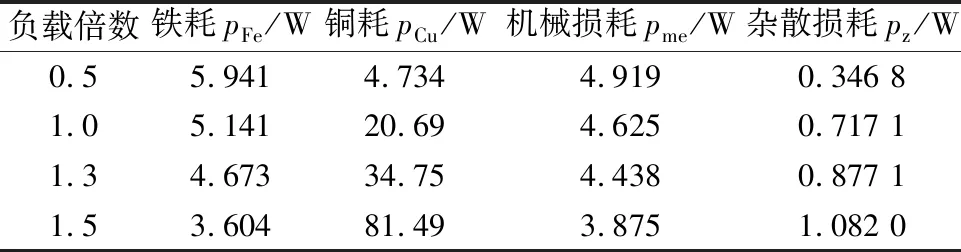
表4 损耗分布表

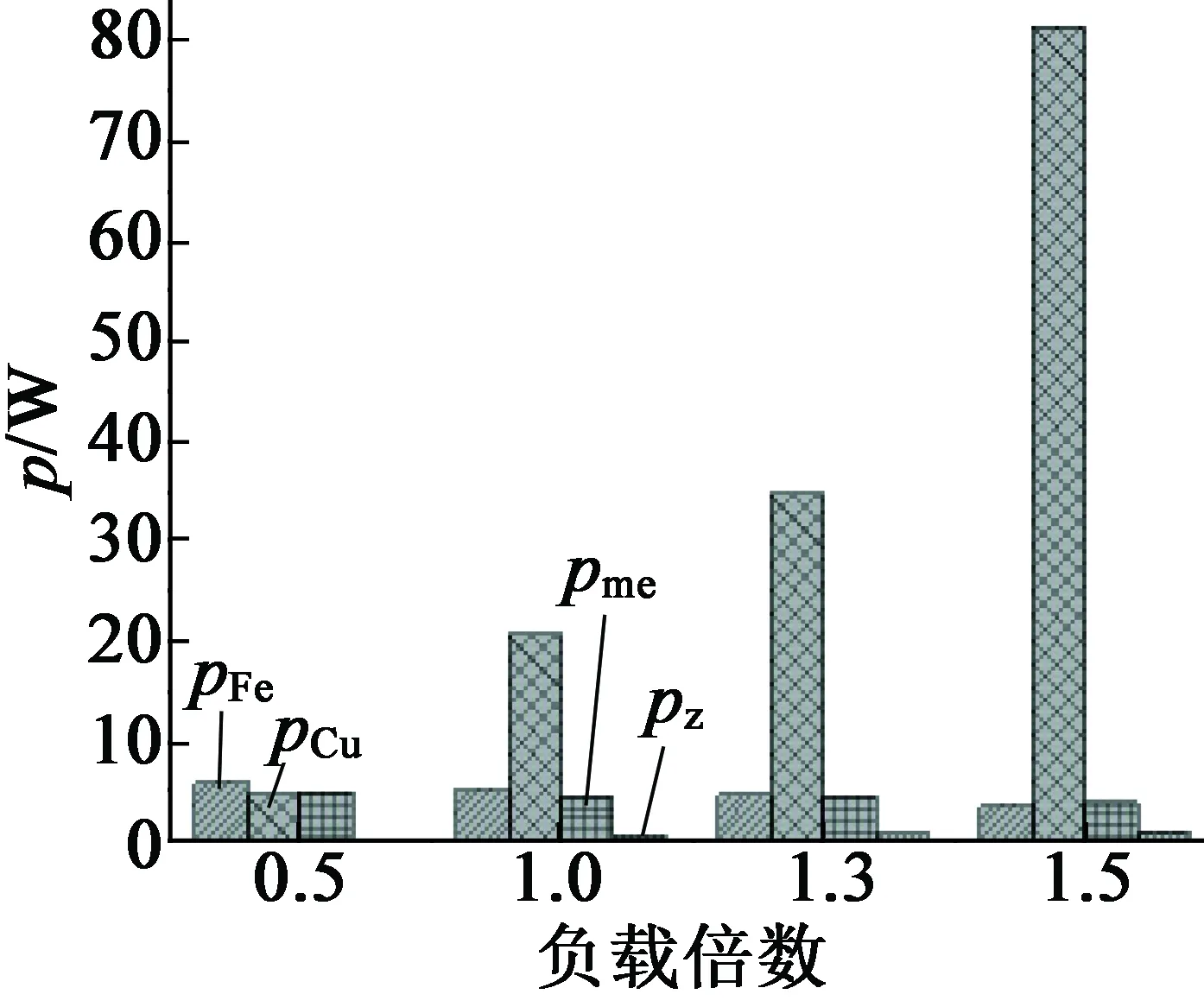
图3 损耗柱状图

从图3和表4中可以看出,随着负载倍数的增大,电机铜耗增加特别明显，电机的其他损耗未发现较大变化。主要是由于电流随着负载增大而增大,导致电机铜耗增大。电机铁耗基本保持不变，由于负载变大、电机转速变慢，电机的机械损耗会减小一部分。另外,电机的杂散损耗是由电机的输出功率乘以一定比例估算的。

3 温升计算

3.1 磁热耦合计算

常见的磁热耦合方式包括单向耦合和双向耦合。单向耦合是只在初始温度下计算电磁损耗，导入热模型中计算温升，计算速度快，所占计算资源小，同时还具有一定的准确度。双向耦合就是电磁热迭代收敛耦合计算，首先由电磁计算出损耗，加载到温度场，然后温升传递给电磁，计算新温度下的电磁损耗，电磁跟温度场计算进行数据交换，计算时间较长，精度较高。考虑到时间及计算的准确度问题，本文选用单向耦合来计算电机的温升。

3.2 不同负载下的温升计算

考虑到电机整体结构复杂，结合实验测试传感器放置的电机部位，由建立的模型分别计算电机在0.5，1.0，1.3，1.5倍额定负载下运行170 min的定转子瞬态温升，包括定子铁心轭部跟齿部、绕组中部、转子端电机外壳。定子齿部和轭部温升图如图4、图5所示；绕组温升图如图6所示；转子温升如图7所示；电机外壳温升如图8所示。通过对比曲线发现，电机负载越大，温升越大，电机在超过一定额定负载倍数时，温升显著。

图4 定子铁心齿部温升图

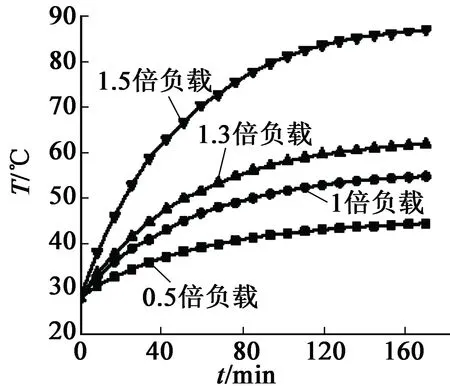
图5 定子铁心轭部温升图

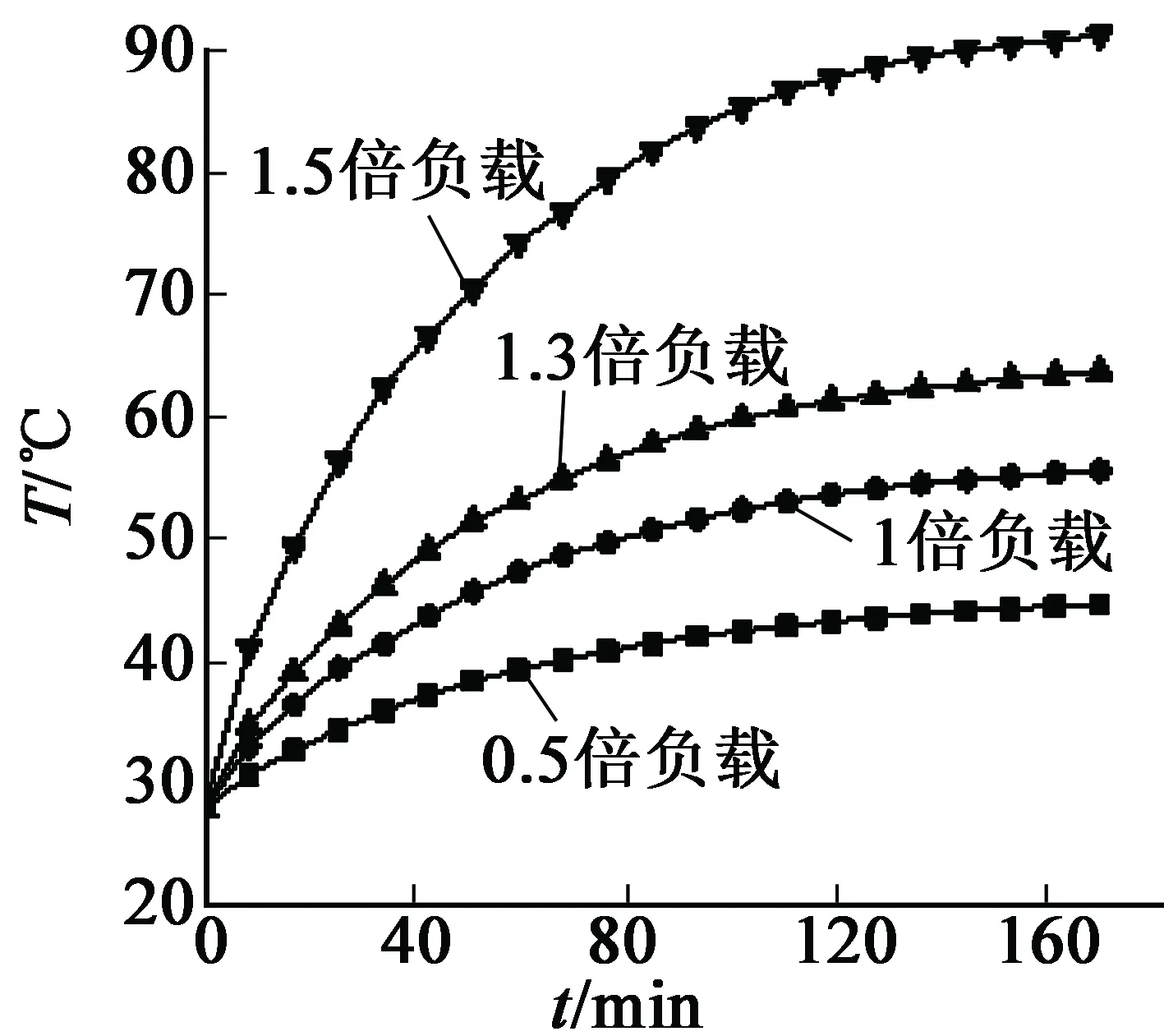
图6 定子绕组中部温升图

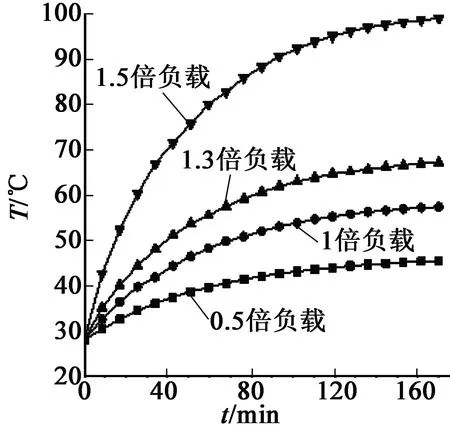
图7 转子端环温升图

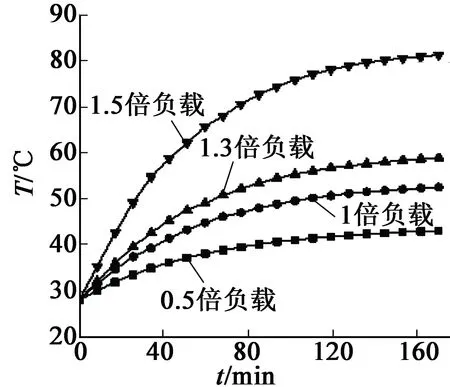
图8 电机外壳温升图

4 实验测试

为了验证温升计算的准确性，搭建了小型异步鼠笼电机温升实验平台，主要由实验电机、负载直流电机及温度采集卡组成，实验设备如图9所示。分别电机的绕组中部、定子铁心外轭部及齿部、电机外壳等部位埋置了热电偶测量电机温升，通过红外激光测温仪测取转子端环的温升。

4.1 不同负载的温升情况

电机带0.5，1.0，1.3倍额定负载运行170 min,各部位的瞬态温升曲线如图10～图12所示。由于测试时间较长，电机在1.5倍负载下电机温升会上升较快,极有可能导致电机烧毁，故不测试1.5倍负载下电机的温升情况。

从图10～图12中可以看出，当电机在0.5倍和1倍负载的情况下，电机的转子端环温升计算与测量值有较大的误差，这是由于转子端环温度是由红外激光测温仪测取的，转子端环在机壳内部，而测温仪是在端盖口处测取温度。同时发现，电机转子在0.5倍和1倍负载的情况下，电机的转子端环温升远远比其他部位高，而电机在1.3倍负载下的绕组温升比转子端环温升大，这主要是因为当电机负载比较小时电机绕组的损耗较小，而随着负载的增加，电机铜耗则加大，所以导致在负载倍数较大的情况下电机绕组的温升也会较大。

另外发现，计算温升普遍小于实验测试的温升。由于计算值是忽略了一些风摩及其他存在的一些影响因素；另一方面，由于采用单向耦合计算温升，以初始温度28 ℃时的电磁损耗来计算温升，忽略了电机损耗会随温升发生变化。

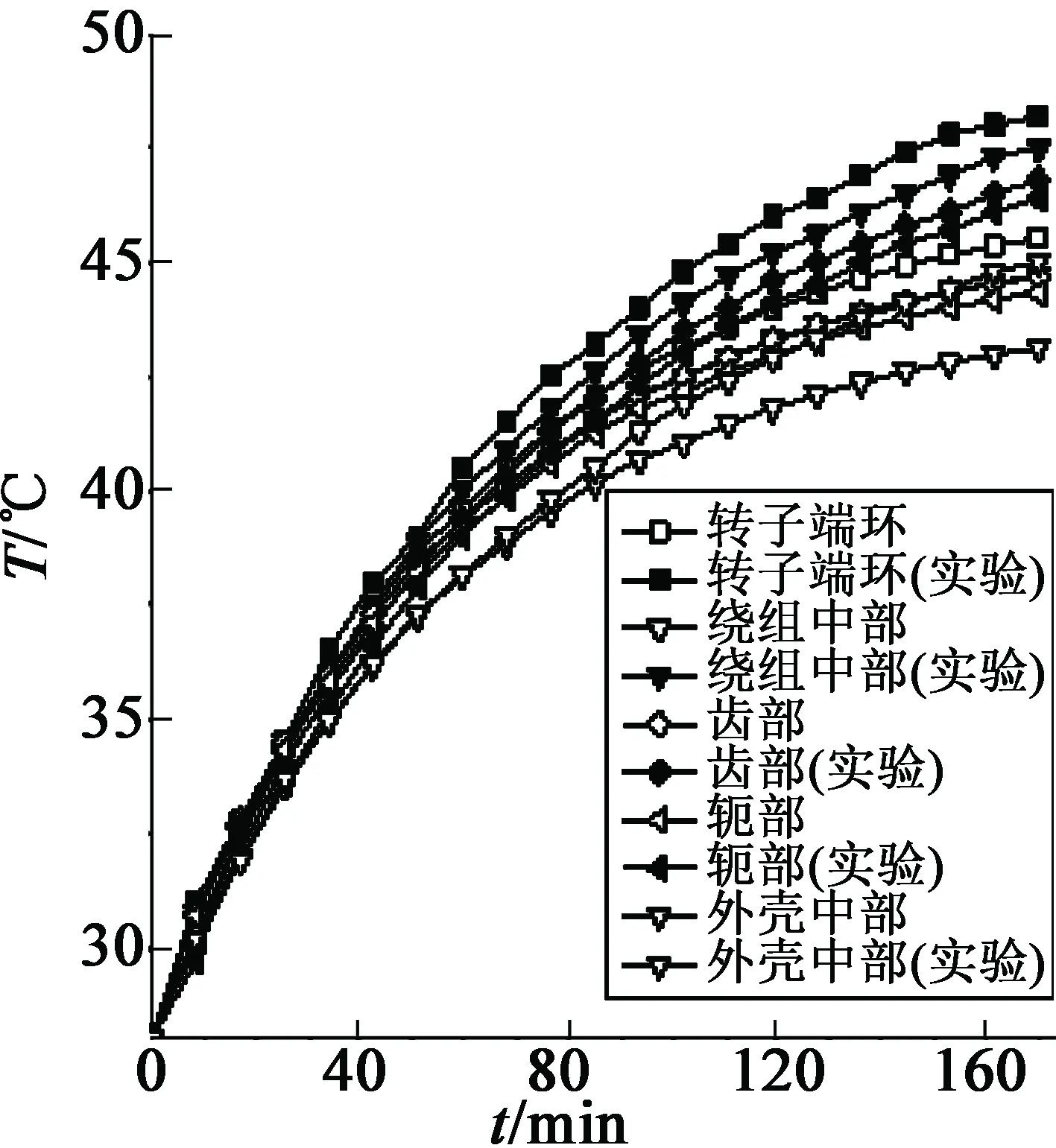
图10 0.5倍负载温升曲线

图11 1.0倍负载温升曲线

图12 1.3倍负载温升曲线

4.2 仿真计算与实验对比

除上文仿真与实验数据曲线对比外，对电机的最终温升进行对比，对比图如图13所示。可以从图13中看出，电机在1.3倍负载时电机的实验测试与仿真计算值存在较大差别。

图13 实验测试与仿真对比图

对电机温升计算值和仿真值求取平均误差率，按照电机各部位最终温升值之差除以电机实验测试值求取各部件温升误差率，最后取所有部件误差率的平均值，求取结果如表5所示。从表5发现，电机在0.5倍，1.0倍负载下的温升能保持较高的准确度。从图13中可以看出，电机在1.3倍负载下的温升计算值存在着较大误差，这是由于温升计算采用单相耦合，电机的负载超过额定负载一定倍数时电机的温升较大，在温度较高时电机损耗远远高于初始计算的损耗。

表5 误差率

5 结 语

本文以一小型异步电机为研究对象，利用软件建立电机热网络模型计算电机的温升。计算了电机在不同负载下的损耗分布及温升情况，结合实验和仿真对比分析。本文得到了以下结论。

1) 此小型异步电机在一般负载运行下的主要温升较明显的部位是电机绕组和电机转子，当电机负载达到一定倍数时电机温升的主要部位就是电机绕组。

2) 通过损耗计算发现，电机在带载额定转矩以下的负载损耗主要是定转子铁耗，而超过了一定倍数后电机的主要损耗就是电机铜耗。

3) 通过实验与仿真计算对比分析，计算电机在0.5，1.0倍负载下的瞬态温度场时，采用磁热单向耦合的方法计算速度快且具有一定的精度。电机在1.3倍负载时温升较大，此时使用磁热单相耦合计算误差较大。