超声波电动机无模型自适应速度控制研究

孙 阳，狄思思，李华峰

(南京航空航天大学 航空学院精密驱动与控制研究所，南京 210016)

0 引 言

超声波电动机是一种微特电机[1]，它利用压电陶瓷的逆压电效应产生超声振动，利用定转子之间的摩擦力，将电能转换为机械能。与电磁电机相比，它具有低速大扭矩、断电自锁、不产生电磁干扰等特点，在某些领域有突出的作用。

超声波电动机涉及材料、机械、电力电子等诸多学科领域，本身又是一个复杂的非线性系统，目前还无法建立较为准确的电机动静态数学理论模型。其非线性因素主要有以下三点：

(1) 压电陶瓷的迟滞非线性[2]：压电陶瓷自身具有迟滞非线性，包括介电迟滞非线性、压电迟滞非线性和弹性迟滞非线性，因此它振幅的大小并不只取决于激励电压的大小，而这对于速度控制是不利的。

(2) 定转子的摩擦损耗[3]：由于超声波电动机的动力传递需要通过摩擦力实现，因而摩擦界面的摩擦特性对超声波电动机的性能有至关重要的影响。而随着超声波电动机工作时间的增加，磨损是必然的，这会影响接触界面的粗糙度和接触特性，从而造成超声波电动机运行特性的变化。

(3) 定转子摩擦带来的温度上升[4]：定转子之间的摩擦会产生大量的热量，导致电机发热严重。温度上升一方面会使定子弹性模量改变，造成共振频率下降；另一方面，温度会影响压电陶瓷的参数，压电系数d31随温度升高而增大，因而使得定子振幅发生变化。

由于上述原因，基于电机模型来设计控制器面临很多困难。因此，学者们研究了数种基于数据驱动的控制算法，用于超声波电动机的速度与位置控制，包括PID控制及其改进算法和各类神经网络控制。文献[5]把驱动信号的电压幅值、频率和相位差作为控制器输出，采用传统PID方法来控制电机的转速和位置。为了增强电机的瞬态响应并提高系统的耐用性，文献[6]中研究者们设计了具有可变学习率的三层在线学习神经网络控制器。然而，这两种控制算法都各有缺陷：PID的控制效果受控制参数影响较大，控制参数选取不当，甚至能导致控制器发散，某种应用场合下通常需要做大量实验才能确定一组最佳参数。神经网络控制虽然具有自适应和自学习能力，但是控制器计算量较大，且需要通过大量数据训练才能适应某种应用场合，实用性不高。

本文将无模型自适应控制(以下简称MFAC)用作超声波电动机速度控制器，并且分别在存在期望速度变化和负载扰动的情况下与传统的PID控制器进行比较。实验结果表明：MFAC能较好地兼顾响应速度和稳定性，且具有出色的自适应跟踪能力和鲁棒性。

1 MFAC理论

MFAC是基于以下离散单输入单输出(SISO)非线性系统发展而来的：

y(k+1)=f[y(k),…,y(k-ny),u(k),…,

u(k-nu)]

(1)

式中：u(k),y(k)∈R，分别表示k时刻系统的输入和输出；ny和nu分别表示输入和输出的阶数；f(…)表示未知的非线性函数。自从1981年Stephen A Billings[7]首次将式(1)作为NARMAX模型来表示非线性自回归滑动平均模型而提出以来，随后的论文中已经证明了它能够表示广泛的非线性系统。

对非线性系统式(1)，必然有一个名为伪偏导数(以下简称PDD)的时变参数Φc(k)，使得式(1)可转化为如下数据模型：

Δy(k+1)=Φc(k)Δu(k)，∀Δu(k)≠0

(2)

式中：Δy(k+1)=y(k+1)-y(k)，Δu(k)=u(k)-u(k-1)。

超声波电动机的速度控制目标是计算得到一个适当的频率u，使得转速误差e(k)=y*(k)-y(k)随着时间增长收敛至无穷小。考虑如下输入准则函数：

J[u(k)]=|y*(k+1)-y(k+1)|2+

λ|u(k)-u(k-1)|2

(3)

式中：λ>0表示权重因子；y*(k+1)为系统的期望输出。然后根据求极小值的方法，可以得到以下控制算法：

[y*(k+1)-y(k)]

(4)

式中：ρ∈(0,1]是步长因子，目的是使控制算法更具一般性。引入λ限制了控制输入的变化并惩罚了输入的变化，否则，当误差变化较大并发生过冲时，控制输入将变化太大。此外，它可以帮助避免控制律中分母为零的奇异情况。当λ小时，系统处于欠阻尼状态，动态偏差较大。 随着λ的增加，过调节和最大动态偏差开始减小，系统的稳定性得到改善。但是增加到一定程度后，响应时间将太长。

由于Φc(k)是系统未知的PPD，不能直接用于式(5)，因此，需要设计PPD估计准则函数：

J[Φc(k)]=|y(k)-y(k-1)-

Φc(k)Δu(k-1)|2+μ|Φc(k)-

(5)

式中：μ>0是权重因子，然后根据求极小值的方法，可以得到以下PPD估计算法：

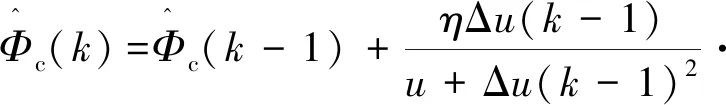
(6)

重置算法：

(7)

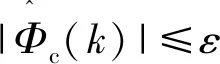
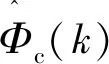
在实际使用时，需要先使用式(6)对PDD进行估算，并判断是否需要使用式(7)进行重置，再将PDD估算值代入式(4)，最终获得控制器的输出u。

2 MFAC算法仿真分析

2.1 建立模型

为了能够有效地进行仿真，需要对超声波电动机建立模型以获得输入输出数据，从而进行超声波电动机速度控制仿真分析。

目前，超声波电动机的物理模型主要是基于对超声波电动机运行机理的分析，得到输入信号与电机输出特性间的关系，从而建立机电耦合模型[8]。而该物理模型具有一定的局限性，例如认为压电陶瓷是理想的线性元件，定转子接触面状态恒定，无温度场影响等。而前面说明了超声波电动机是一种强非线性的控制对象，同时我们分析了造成超声波电动机非线性的因素，而这些非线性因素目前还无法用物理公式精确表达。因此，想要对超声波电动机建立高精度的物理模型不太可能。

因此，本文通过对超声波电动机进行离线参数辨识的方法来获得传递函数。整个辨识流程如图1所示。

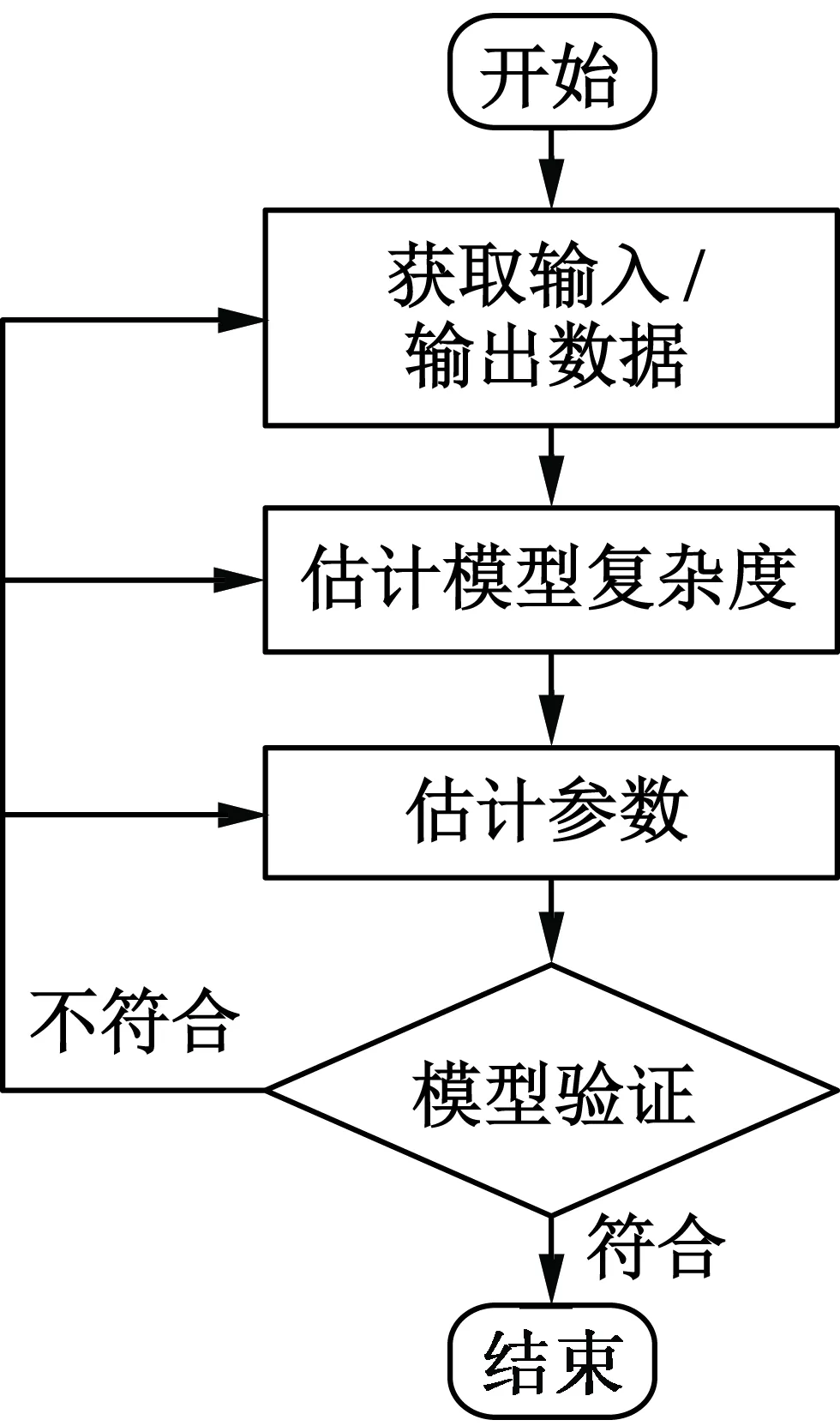
图1 系统辨识流程图

系统辨识时，要选择频谱合适的电机输入信号，要求不仅能包含辨识对象的带宽，幅值也不能太大。因此，我们选择伪随机二进制序列(PRBS)来作为输入电压信号。

为了使辨识得到的模型稳态增益具有较高的准确性，PRBS序列中的最大脉冲持续时间要大于对象的上升时间tR。为了覆盖某一PRBS所产生的全部频谱，测试的时间长度L至少要和序列的长度一样，即满足以下条件：

(8)

本文设置采样周期为2 ms，测试时间5 s，超声波电动机开环性能显示其上升时间一般为9～10个采样周期。因此选择PRBS7作为激励信号，此时PRBS7的序列长度为256 ms，远远小于测试时间。

图2为PRBS7激励信号。图3(a)和图3(b)分

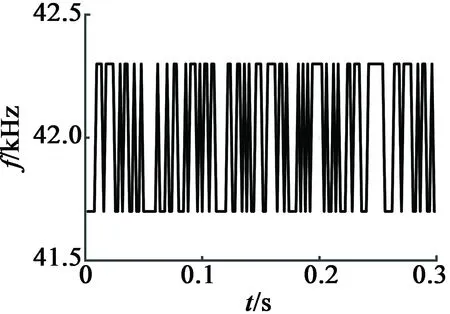
图2 PRBS7激励信号

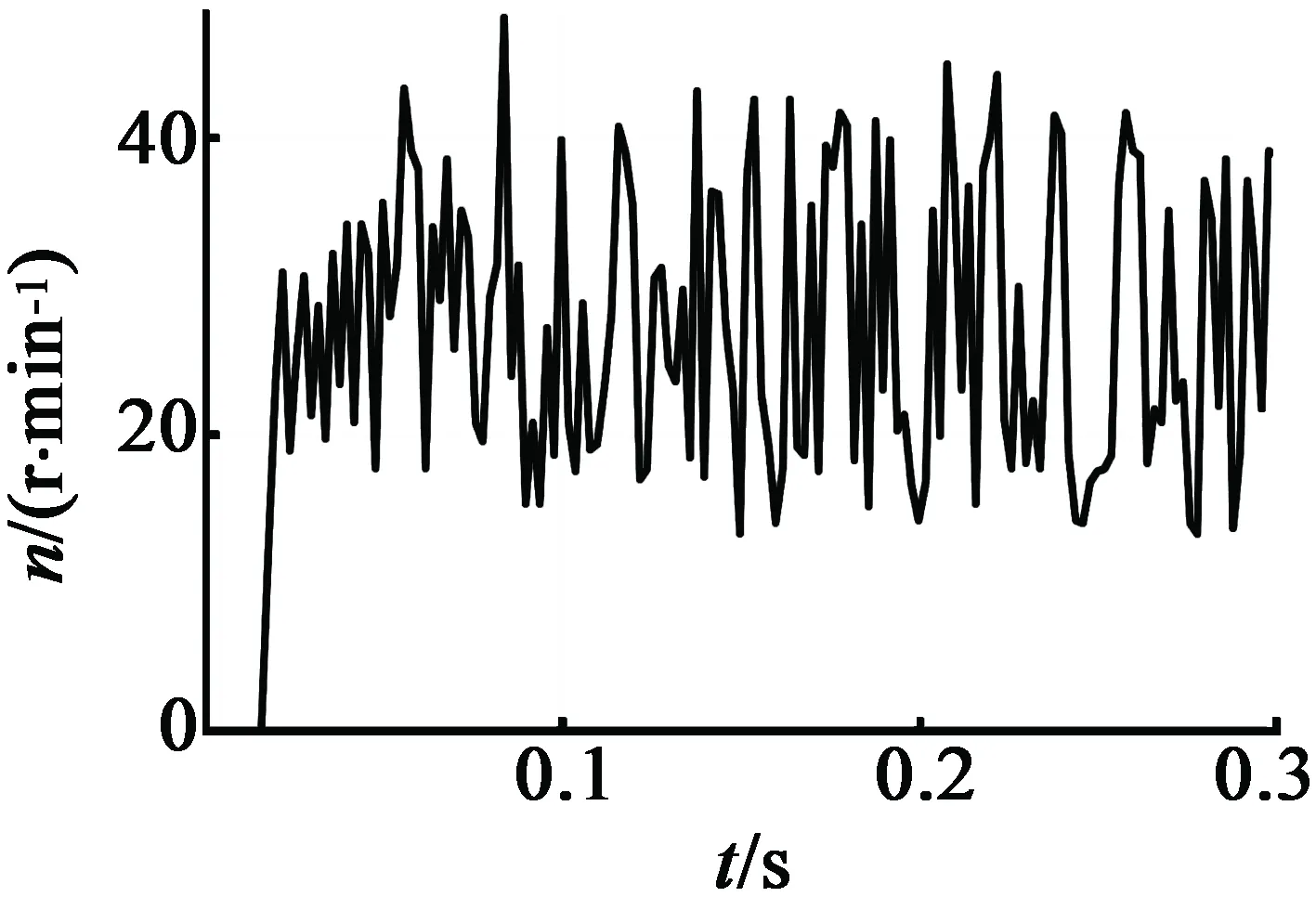
(a) 不带负载

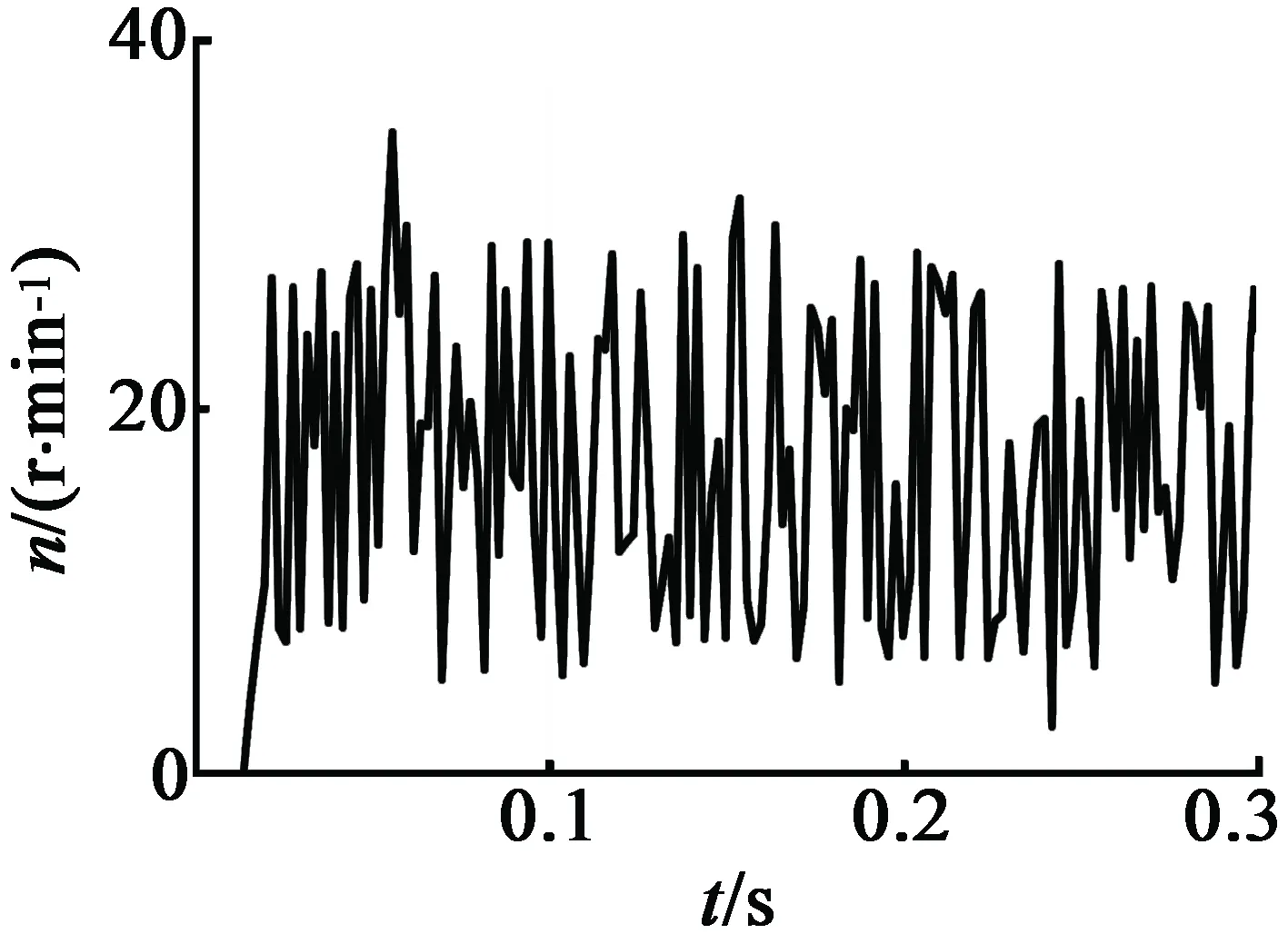
(b) 0.5 N·m负载

别是不带负载和带0.5 N·m负载下的系统输出信号，图3中仅显示一个脉冲序列长度的系统输入/输出信号。随后采用增广最小二乘法(ELS)来辨识系统，设系统的传递函数：

(9)

式中：n为系统阶数。

不带负载下五阶和六阶系统参数辨识结果如下：

带负载下五阶和六阶系统参数辨识结果如下：

将f=42 kHz作为系统输入，分别代入不带负载和带负载情况下的五阶和六阶系统传递函数中，得到系统输出曲线与实验数据的对比图,如图4所示。从图4中可以看出，两种情况下五阶和六阶系统输出曲线与实验结果较为接近，因此选用六阶模型作为仿真模型。

(a) 不带负载

(b) 带负载

2.2 仿真研究

给定MFAC一般性的算法参数如下：λ=ρ=μ=η=1。为了说明MFAC算法的有效性，分别用MFAC算法和PID算法对两种六阶模型进行速度控制。图5(a)、图5(b)分别是不带负载时MFAC和PID(P=0.01,I=0.4,D=0)作用下超声波电动机转速图和转速误差图；图6(a)、图6(b)分别是带0.5N·m负载时MFAC和PID(P=0.02,I=0.56,D=0)作用下超声波电动机转速图和转速误差图，其中期望速度为30 r/min。PID参数是多次整定后取最优值。从图5、图6中可以看出，MFAC和PID都取得了令人满意的效果，MFAC比PID的误差略小，上升时间略快。

(a) 转速

(b) 转速误差图

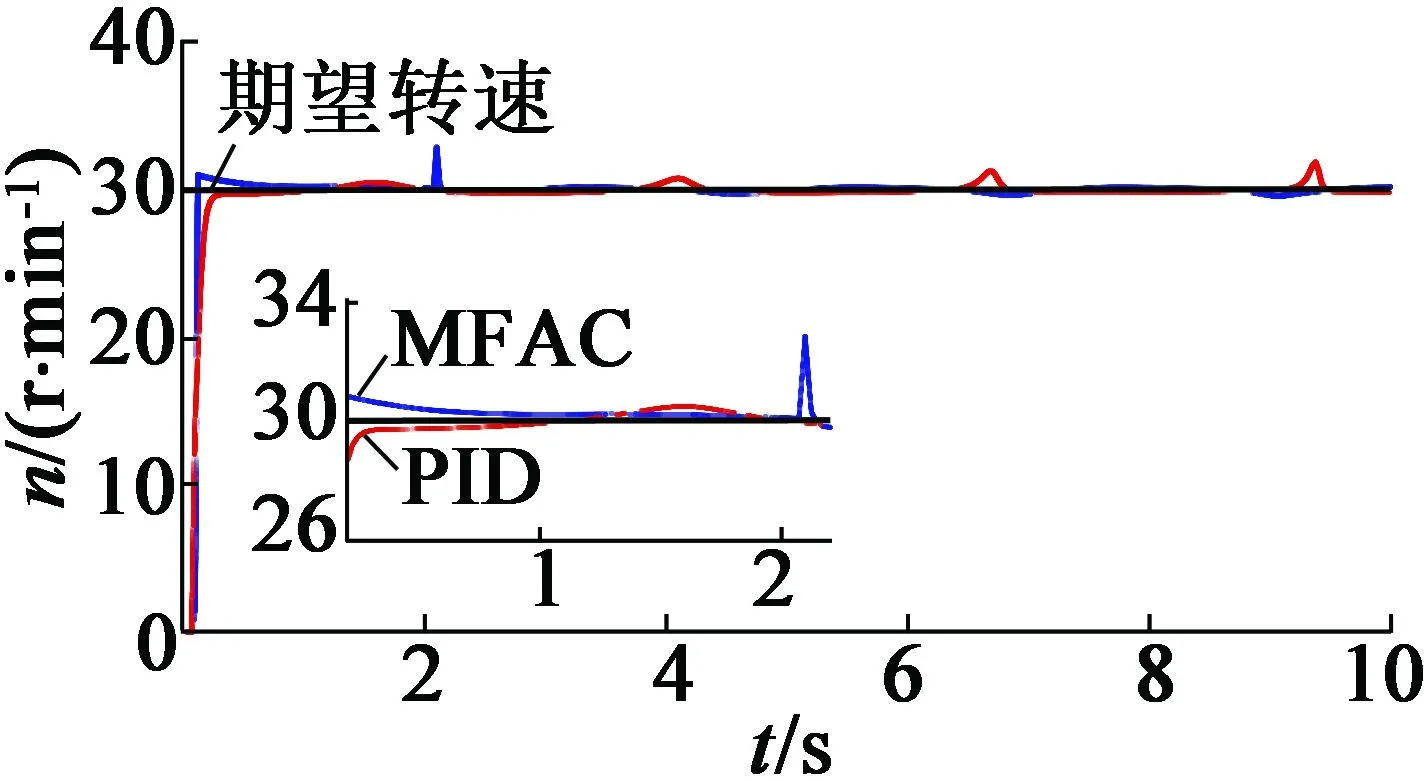
(a) 转速图

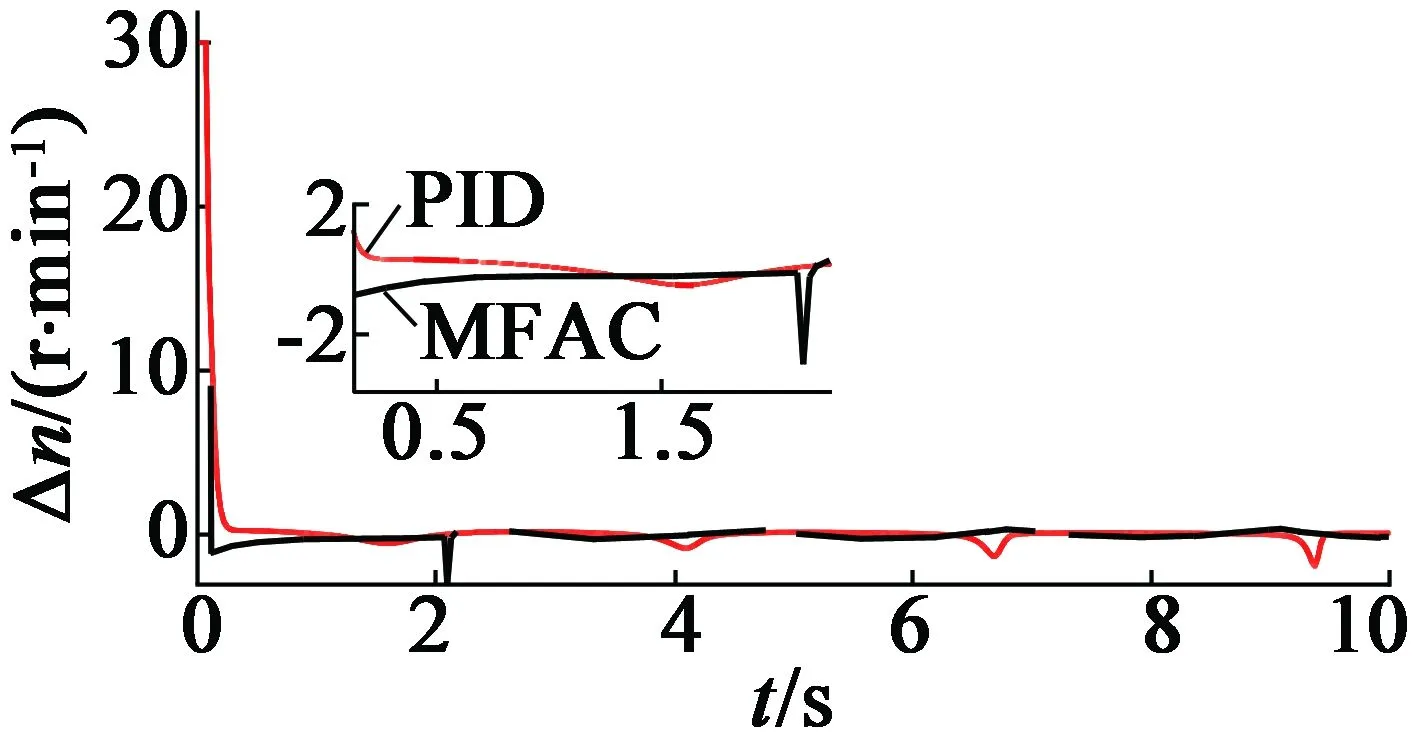
(b) 转速误差图

3 MFAC实验验证

为进一步验证MFAC算法的控制效果，在搭建的超声波电动机控制平台上进行方波速度跟踪、正弦波速度跟踪和变负载跟踪实验，并与PID控制进行比较。其中，PID参数都为各自实验条件下多次整定后的最优值，MFAC的控制参数统一取为：λ=ρ=μ=η=1。图7为超声波电动机控制平台，其中MCU用于读取编码器值，并与PC和FPGA通信，FPGA用于产生高分辨率(0.1 Hz)的SPWM信号，经过推挽放大电路后驱动超声波电动机。超声波电动机为南京航达超控科技有限公司生产的TRUM60型超声波电动机。

图7 超声波电动机控制平台

图8(a)展示了MFAC和PID作用下方波速度跟踪曲线，PID参数：P=6.12，I=8.86，D=0。MFAC的误差保持在4.22%以内，上升时间为20 ms，而PID的误差在5.46%以内，上升时间为30 ms，从图8(a)中也可以明显看出,MFAC的跟踪特性要优于PID。图8(b)展示了MFAC作用下输出频率和Φ的曲线，其中Φ已在式(2)中定义，表示改变频率造成电机转速变化的程度。随着时间的增加，电机内部由于定转子之间的摩擦力作用及定子高频振动产生的热量大量堆积，温度剧烈上升，从而使电机共振频率下降，为了获得相同的转速，需要用更小的频率去驱动电机。从图8中也可以看出，0～1.25 s时，当期望转速为10 r/min时，电机驱动频率离共振点较远，温度上升不高，此时电机性能稳定，Φ几乎不变。1.25～2.5 s时，当期望速度突变至50 r/min时，驱动频率迅速减小到41.55 kHz附近，离电机共振频率较近，电机温度上升造成共振频率下降，而转速对频率的斜率越来越大，因此Φ逐渐增大。2.5～3.75 s时，期望转速又突变至10 r/min，电机发热量迅速减小，共振频率不再明显下降，转速对频率的斜率又恢复至稳定值。因此,MFAC的参数Φ可以在一定程度上代表电机运行性能。

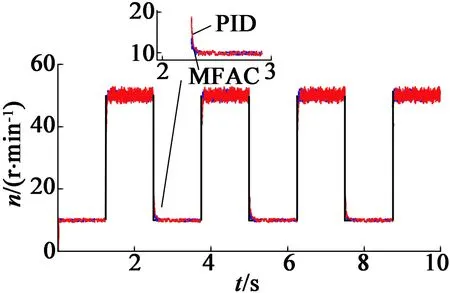
(a) MFAC和PID作用下方波速度跟踪曲线

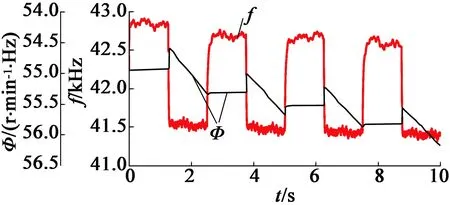
(b) MFAC作用下输出频率曲线和Φ曲线

图9(a)展示了MFAC和PID作用下正弦波速度跟踪曲线，PID的参数：P=9.21，I=9.05，D=0，上升时间为35 ms；MFAC的上升时间为25 ms。从图9(a)中可以看出，两种控制算法对转速在10 r/min以上均能有效控制，MFAC的误差保持在4.84%以内，PID的误差保持在5.87%。而转速在10 r/min以下时，均表现出误差过大，这主要是因为超声波电动机在低速运行时，由于驱动频率离共振频率较远，此时无论是PID还是MFAC都较难以在短时间内将驱动频率收敛至合适值，因此低速时都表现出误差过大和转速跟踪性能下降的情况。这一点在图9(b)中也能得到验证，当在1.25～2.5 s内，理论上Φ应该呈现出先较快减小后较快增大的趋势，而实验中Φ却一直较慢减小，表明并未跟踪至极小值附近，因而呈现出低速时误差过大和跟踪性能下降的情况。

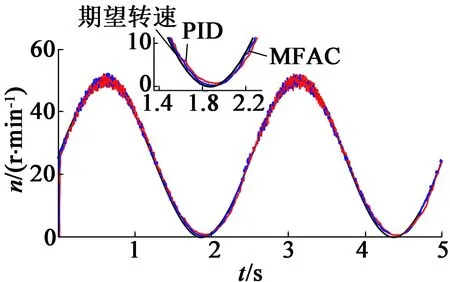
(a) MFAC和PID作用下正弦速度跟踪曲线

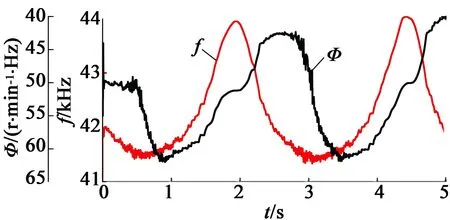
(b) MFAC作用下输出频率和Φ曲线

图10展示了MFAC和PID作用下变负载跟踪曲线。负载如下：

PID的参数：P=10.43，I=8.25，D=0，上升时间为25 ms；MFAC上升时间为15 ms。在0～2.5 s和5～7.5 s时间段中， MFAC的误差保持在4.97%以内，PID的误差保持在5.18%以内。而在2.5～5 s和7.5～10 s时间段中，MFAC的误差保持在5.43%以内，PID的误差保持在13.33%以内。这主要是因为某一组PID参数很难适用于超声波电动机运行的各种工作情况，实际工作情况变化较大时需用多组PID参数进行控制。而MFAC表现出较好的鲁棒性能，一组参数就能在负载突变的情况下保持较高的稳定性。

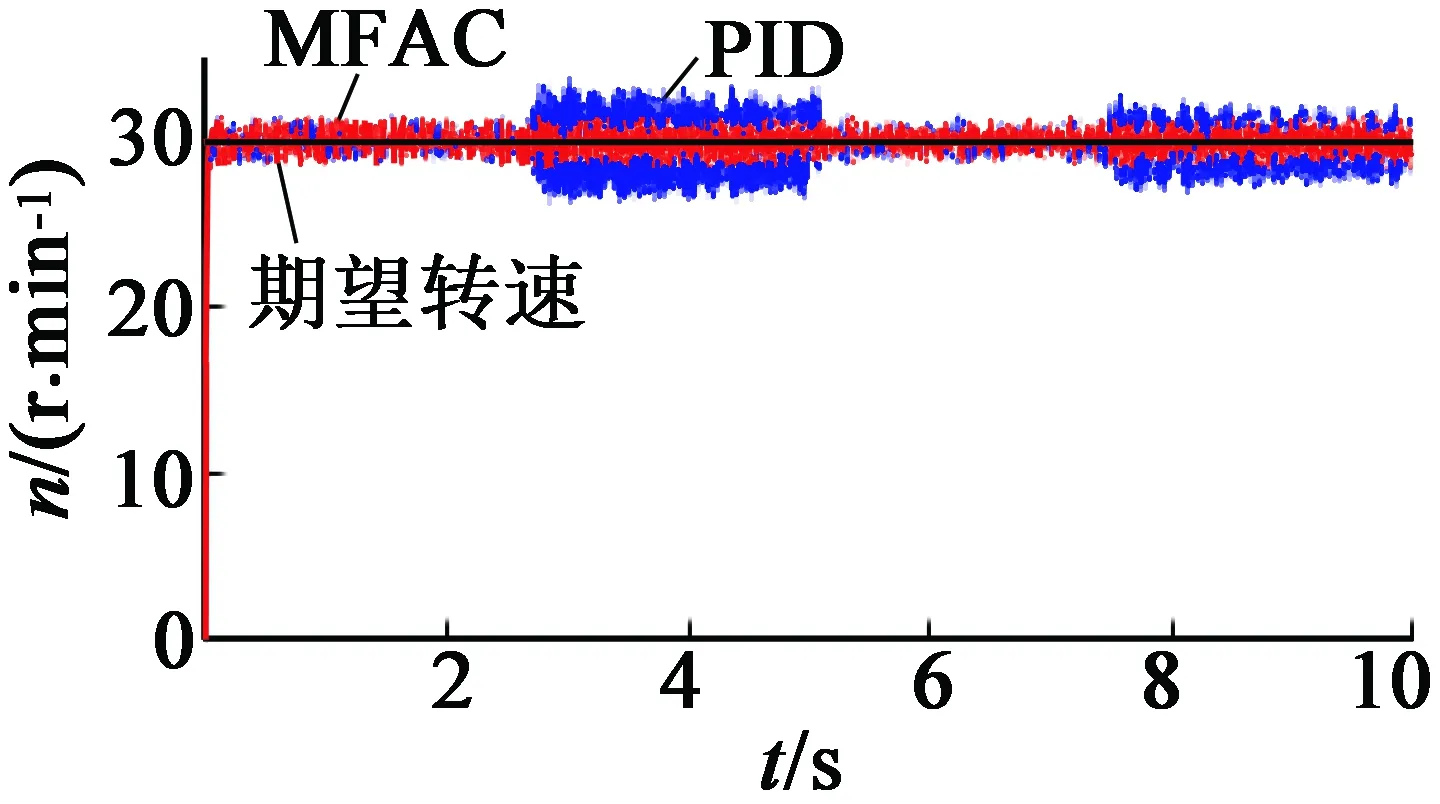
图10 MFAC和PID作用下变负载速度跟踪曲线

三组实验数据表明：相比于PID控制，MFAC在参数整定上更加容易，又能保证较好的跟踪性能，这在实际应用中有较好的优势。

4 结 语

本文从超声波电动机速度控制的角度出发，对MFAC进行详细描述。超声波电动机存在建模困难的问题，采用PRBS7对超声波电动机进行在线参数辨识，获得具有较高精度的模型。随后利用该模型，分别用MFAC和PID进行仿真，表明MFAC的有效性。最后分别进行MFAC和PID在方波速度跟踪、正弦波速度跟踪和变负载跟踪实验。实验结果说明，相较于PID控制，MFAC具有一定的鲁棒性和自适应性，说明该控制策略是一种行之有效的方法，且具有实际工程应用价值。