面向城市作战的目标威胁排序方法研究

毛保全，李元超，杨雨迎

(陆军装甲兵学院 兵器与控制系，北京 100072)

随着城市化进程的加快，部队将遂行城市攻防作战、反恐作战以及防暴维和行动，城市作战已成为陆军的主要作战样式。未来部队在城市作战中面对的威胁具有全方位、立体化、距离近、目标分散、灵活及隐蔽等特点，不易发现和打击，因此，如何实现对目标的智能化精确打击是目前城市作战所面临的难题。

要实现城市智能化作战，需要作战平台能够为作战指挥员提供城市作战中目标的智能识别、威胁排序、火力决策以及毁伤评估等全链路辅助决策信息，才能达到快速发现目标、智能精确打击的作战目的。其中目标威胁排序是智能化作战的重要组成部分，威胁排序方法在不同作战领域进行深入的研究，特别是空中和海上作战，取得了广泛的应用。但是，在地面作战中，目标威胁排序的实际应用难以满足智能化作战需求[1]。一方面由于目前的战场感知技术准确性和实时性达不到作战要求，如果单靠作战平台自身传感器获取，则识别准确性较差；如果多次结合人工经验修正识别数据，那么就会造成从目标识别到威胁排序过程时间较长，影响平台射击反应速度。另一方面因为地面作战环境复杂，需要量化的威胁指标较多，采取的方法手段多样，同一指标在山地作战和城市作战判定准则存在一定差异。所以，地面作战进行目标威胁排序需要在区分作战环境的前提下，将作战平台通过图像信息以及多传感器数据融合等方式探测和识别的目标信息作为威胁排序的输入条件，直接给操纵者提供威胁排序结果，操纵者确认目标威胁排序的结果后，立即对威胁最大的目标进行打击，缩短作战平台的射击反应时间，尽量达到先敌开火，攻击要害，从而提高武器平台的作战效能。

笔者提出城市作战环境下的目标威胁排序方法研究，构建了目标威胁评估指标体系，结合城市作战实际情况对评估指标量化方法进行介绍。采用更加合理的评估指标赋权法，再运用TOPSIS法[2]对不同目标的威胁程度进行排序，并通过实例验证该方法的有效性。

1 指标体系的构建及指标量化方法

1.1 指标体系的构建

根据城市作战环境的特点，结合目标识别的各类指标信息，区分定性和定量指标，对当前地面目标威胁评估指标进行完善，建立如图1所示的指标体系。

1.2 指标量化方法

1.2.1 定性指标量化

定性指标在量化时，通常采用模糊评价语言[3]的方法进行量化处理，设威胁模糊评价语言标度L=9，具体的量化标尺如表1所示。

表1 量化标尺对应值

1.2.1.1 目标类型

从目标图像识别的角度，对城市作战可能遭遇的目标类型进行了细分，按照威胁等级从大到小依次为：低空直升机、低空飞行器、轮式装甲车、履带式装甲车、轻型越野车、武装分队和单个人员，可对应量化标尺中很大至很小之间的7级。

1.2.1.2 携带武器

地面常用直瞄武器按照威胁程度大小可分为：导弹、大口径火炮、小口径自动炮、火箭筒、重型机枪、轻型机枪、狙击枪、步枪、手枪，可依次对应9级量化标尺。

1.2.1.3 攻击状态

将目标的攻击状态威胁划分为以下3级：3级表明目标正在对我方进行攻击，对应评价等级为很大；2级表明目标已经发现我方，准备向我方攻击，对应评价等级为中等；1级表明目标暂时没有攻击意图，对应评价等级为很小。

1.2.1.4 通视情况

根据敌我之间有无视线遮挡，将通视情况区分敌我通视、部分遮挡和完全遮挡，对应的评价等级分别为很大、中等和很小。

1.2.2 定量指标量化

定量指标是我方作战平台利用传感器精确测量得到，其威胁度大小受敌我双方实时位置关系的变化而改变，可以通过建立威胁度函数的方法进行指标量化[4]。

1.2.2.1 目标距离

目标距离指标是衡量目标威胁度的一项重要参数[5]，传统的目标距离指标量化只考虑双方的之间距离的大小，认为距离越远，则威胁越小。城市作战所面临的多数目标距离都比较近，因此还需要考虑敌我双方武器的最大攻击距离，综合衡量目标的距离威胁度。设Id为距离指标威胁度，D为双方之间的距离，Dw为我方武器最大攻击距离，Dd为敌方最大攻击距离，根据这三者之间的关系，建立以下距离威胁度函数：

当D≥Dd时，

Id=0.

(1)

当Dd>D>Dw时，

Id=1.

(2)

当Dd>Dw>D时，

(3)

当Dw>Dd>D时，

Id=1-0.9D/Dd.

(4)

1.2.2.2 目标速度

目标速度指标反应了目标运动状态的威胁程度，当目标运动速度越快，我方对其进行探测和打击的难度越大，因此判定其对我方的威胁度越大，这里主要考虑目标速度数值的大小。设Iv为速度指标威胁度，v为当前目标的速度大小，vmax为目标的最大速度值，建立的速度威胁度函数为

Iv=βv/vmax，

(5)

式中β为目标速度系数，根据目标的类型确定，通常分为空中目标、车辆目标和人员目标三类，系数取值分别为：1，0.8，0.5.

1.2.2.3 打击角度

打击角度是指目标武器打击方向与双方作战平台之间连线的夹角[6]，当目标武器打击方向指向我方作战平台，我方火力打击方向指向目标的反向，此时目标的威胁度最大；目标火力打击方向指向我方武器平台的反向，我方火力打击方向指向目标，此时目标的威胁度最小，一般情况如图2所示。

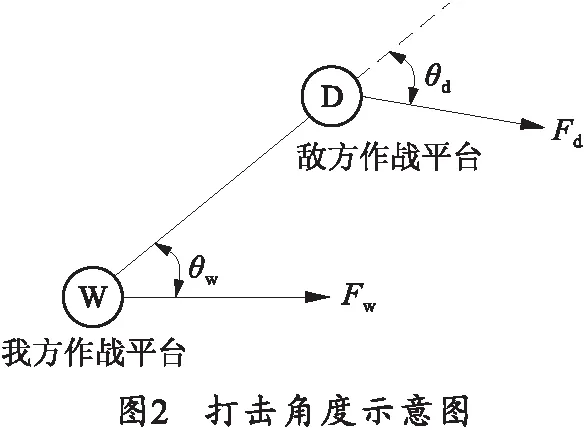
设Iθ为打击角度指标威胁度，θd为敌方作战平台的攻击角度，θw为我方作战平台的攻击角度，建立的威胁度函数为

Iθ=(θd+θw)/360.

(6)

1.3 威胁度矩阵的建立

目标威胁排序本质上是一个多指标决策问题[7]，将多个目标的威胁度指标量化后，最终建立一个威胁隶属度矩阵Xij=[xij]m×n，其中xij为第i个目标、第j项指标的威胁度。

2 指标权重的确定

2.1 专家打分主观赋权

为了保证主观赋权的准确性，笔者到多个院校、研究所和基层部队等单位调研，选取9名武器系统领域的专家，对目标威胁排序的各项指标进行主观赋权打分，得到结果为

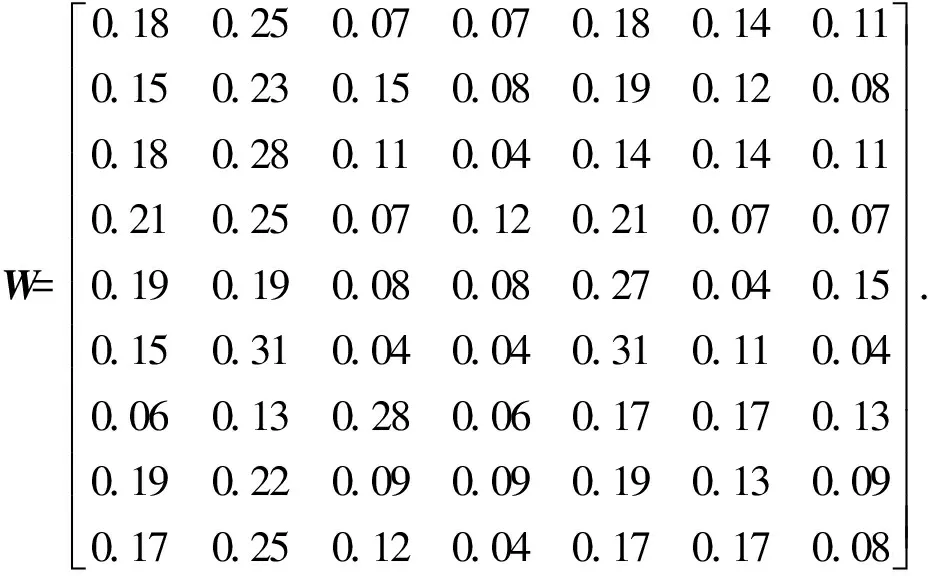
2.2 格拉布斯准则剔除异常值

尽管专家是从事该领域权威人士，但是在进行指标权重打分的时候，通常会有个别专家的看法与其他专家不一致的情况，造成其权重评定值与其他人差别较大，如果将此结果用于后续的计算，则会极大地影响权重计算的准确性，因此采用格拉布斯准则[8]将其剔除。具体步骤如下。

2.2.1 计算权重矩阵的相似程度

通过比较两个专家对某个指标的差异，可以得到不同专家之间对该指标的相似程度，其计算公式如下[9]：

(7)

式中：m为指标数量；Whi表示第h个专家对第i个指标权重的打分值;Rhg表示专家h与专家g对第i个指标评估的相似程度。

通过式(7)，计算得到9个指标的相似度矩阵R为

2.2.2 计算偏离度

偏离度可以通过对每个专家所有指标的相似度求和得到，计算公式为

Ph=∑Rhg.

(8)

根据式(8)得出每名专家对打分集合的偏离度向量：

P=(P1,P2,…,P9)T=(8.626,8.612,8.569,8.541,8.445,8.377,8.168,8.637,8.597).

2.2.3 对专家的偏离度进行剔除

1)偏离度排序。这里采用升序的方法进行排列： 8.168， 8.377，8.445，8.541，8.569，8.597，8.612，8.626，8.637.

2)求平均值和标准差。计算结果：平均值为8.508，标准差为0.155.

3)求最大值的Gn和最小值的G1.最大值的Gn=(最大值-平均值)/标准差：Gn=0.832；最小值的G1=(平均值-最小值)/标准差：G1=2.194.

4)选择检测水平α，剔除异常值。通常取α=0.05时，查格拉布斯表得到临界值G(9)=2.11，将G(9)与G1、Gn作比较，若G1或Gn大于临界值，应该删掉，反之则予以保留。因为G1>2.11，所以对最小值进行剔除，对应专家编号为7号。

5)循环检验。重复执行上述过程，直至没有数据需要剔除，对于剔除掉的专家，其权重数值作废，保留其他专家打分数值。经过循环检验，只有7号专家打分值异常，进行了剔除，则剩余有效专家个数是8个。

2.3 基于灰色关联分析法的客观赋权

灰色关联分析法即假设知道某一个指标可能是与其他的某几个因素相关的，那么若要知道这个指标与其他哪个因素相对关系更大，哪个因素相对关系弱，依次类推，把这些因素排个序，得到一个分析结果，就可以知道关注的指标与因素中的哪些更相关[10]。笔者使用灰色关联分析法来确定各个指标的权重，并将相关联的参考数据列称为母因素数据列，选取有效专家在每个指标中打分的最高分数作为母因素数据列。

2.3.1 计算关联度系数

设有m个指标，每个指标被n个有效专家打分，则：

x1(t)=(x1(1),x1(2),…,x1(m))，

x2(t)=(x2(1),x2(2),…,x2(m))，

……

xn(t)=(xn(1),xn(2),…,xn(m)).

关联度系数是对于两个系统之间的因素随时间或不同对象变化的关联大小的度量，计算公式为

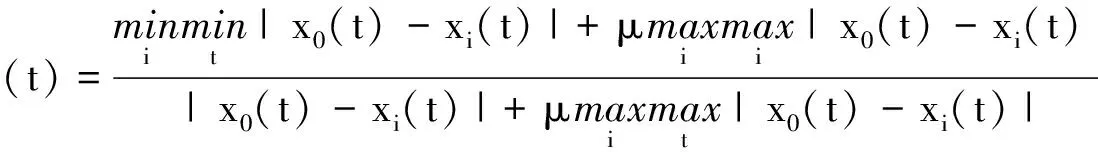
(9)

2.3.2 计算每个指标与母因素数据列的关联度

关联度计算公式为

(10)

通过计算得到母因素数据列为

{0.25,0.23,0.28,0.25,0.27,0.31,0.22,0.25}.

通过式(9)、(10)计算母因素数据与其他因素关联系数和关联度，结果如表2所示。

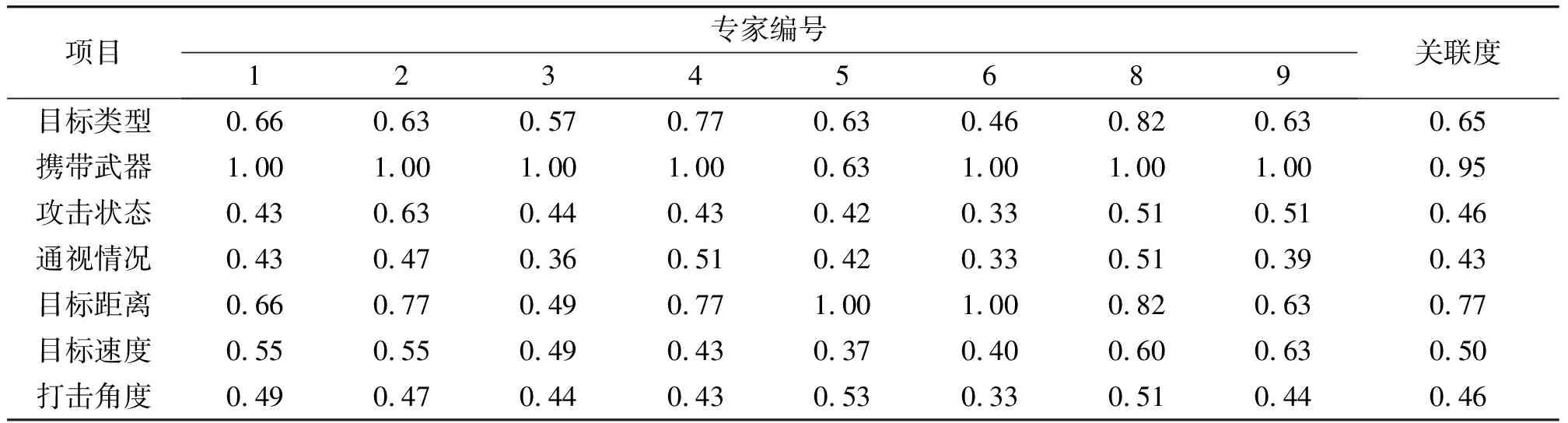
表2 x0与其他因素的关联系数和关联度

2.3.3 计算指标权重

将各指标关联度进行归一化处理后，得到最后权重为

w={0.153,0.226,0.110,0.101,0.182,0.119,0.108}.

3 基于TOPSIS法的目标威胁排序

TOPSIS法是一种常用的多指标决策排序方法。利用TOPSIS法进行目标威胁排序，一般先将指标量化后的威胁度矩阵进行规范化和加权处理，得到标准化的矩阵，再通过确定正、负理想解，得到最优目标和最劣目标，分别计算各评估目标与正、负理想解的距离，最后按照各评估目标与理想解贴近度的大小进行威胁排序[11]。

3.1 威胁度矩阵规范化和标准化处理

为了实现多个威胁目标同一指标威胁度的归一化处理，对威胁隶属度矩阵X采用向量归一法进行规范化处理[12]，得到规范化矩阵Y=[yij]m×n，其中，

(11)

将Y与w相乘，得到加权标准化矩阵Z：

Z=[zij]m×n=[wjyij]m×n.

(12)

3.2 计算到正、负理想解的距离

正理想方案Z+和负理想方案Z-：

(13)

(14)

到正理想解的距离为

(15)

到负理想解的距离为

(16)

3.3 计算相对贴近度并排序

计算第i个目标的相对贴近度Ti：

(17)

Ti值越大，表明评估目标的威胁度量值越大，设目标威胁集T={T1,T2,…,Ti,…,Tm}，根据Ti的大小对目标威胁集进行排序。

4 实例分析

为检验目标威胁排序方法的合理性，对城市作战典型实例进行分析，具体作战假设如下：我方作战平台正在进行城市维稳作战，当前作战平台的运行速度是20 km/h，武器攻击方向与平台运行方向一致，最大攻击距离是1 500 m，通过作战平台探测和操纵者经验判断确认周围敌方目标威胁信息如表3所示。

表3 目标的威胁信息

按照威胁指标量化的改进算法得到目标威胁度矩阵X：

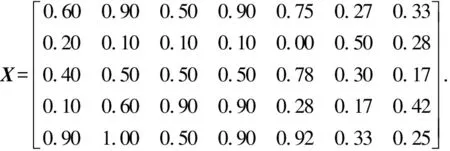
对目标威胁矩阵X采用向量归一法进行规范化处理，根据式(11)、(12)，得到标准化矩阵：

根据式(13)、(14)计算得到Z+和Z-：

Z+=[0.117，0.145，0.079，0.056，0.116，0.080，0.067]，

Z-=[0.013，0.015，0.009，0.006，0.000，0.027，0.027].

根据式(15)、(16)计算得到D+和D-：

D+=[0.071,0.216,0.120,0.154,0.052]，

D-=[0.177,0.058,0.129,0.124,0.214].

根据式(17)计算可得到5个目标的相对贴近度：

T=[0.715,0.212,0.520,0.448,0.806].

按照Ti值的大小进行排序：

T5>T1>T3>T4>T2.

所以，得到5个目标的威胁程度排序结果：携带导弹的武装直升机>装备大口径火炮的轮式装甲车>装备重型机枪的轻型越野车>携带火箭筒的单兵>装备步枪的武装小分队。通过向权威专家请教，该排序结果与主观经验认识相符，可以说明该方法的合理性。

5 结束语

笔者针对城市作战中多目标威胁排序问题，对原有的目标威胁评估指标体系进行完善，对指标量化方法加以改进，使其区别于山地作战条件下指标量化标准，更加符合城市作战的特点；并且提出基于格拉布斯-灰色关联的指标权重确定方法，运用逼近理想解法对目标威胁程度进行排序。通过实例应用，验证该方法可以为城市智能化作战指挥决策提供重要数据支撑。