基于多分类SMM的高噪声图像分割研究

王燕贞，陈志翔

（1.漳州职业技术学院信息工程学院，福建漳州363000；2.闽南师范大学物理与信息工程学院，福建漳州363000）

图像分割是计算机视觉和图像分析处理的关键技术.由于各种原因，如设备缺陷、光照、采集传输等经常会造成图像存在灰度不均匀和噪声问题.这些因素都会降低了图像的分割精度.如何提高算法对噪声图像的分割精度和鲁棒性是一个挑战性课题.

图像分割总体可以分为基于结构和基于概率统计两类方法.基于结构最具代表性的是水平集方法，可分为基于边缘和区域两类模型.1997年Caselles 等提出活动轮廓逼近目标边界方法后，很多学者相继提出基于边缘的改进算法，文献[1]引入可变区域系数结合改进的边缘停止函数区分噪声和边缘.文献[2]在局部边缘熵基础上，重新定义边缘熵拟合能量函数以降低噪声对图像分割的影响.传统的基于区域的模型无法分割灰度不均匀的图像，因此很多改进算法被提出，文献[3]用邻域信息定义能量泛函，结合正则项、弧长项合并到变分水平集公式中以达到去噪效果.但是这些方法对于存在高噪声和灰度不均的图像分割效果仍不佳.为了解决灰度不均和噪声带来的问题，唐文杰等[4]先使用Haar小波对含有噪声和偏移场的医学图像进行分解，从而获取高频低频子图分别存储图像的纹理细节和灰度，与此同时抑制噪声.在四相双水平集的基础上引入偏移场进行建模，分割低频子图后结合高频子图获取粗分割结果，使用模型再次分割，得出最终结果.该方法克服了传统水平集算法边缘分割不清的缺陷，但由于进行了图像分解和两次分割，耗时较长.文献[5]针对亮度不均匀提出一种基于水平集的多尺度局部区域分割模型（MSF）.首先建立圆形区域通过多尺度滤波获取局部强度信息，其次对归一加权图像构造水平集能量泛函，最后依据最小化能量泛函准则实现图像分割.黄国鹏等[6]在文献[5]的基础上，通过对多尺度滤波进行微调来模拟偏移场，在一定程度上降低灰度不均匀对分割的影响.在图像经过预处理后，再分别构建基于偏移场校正和局部区域的两个能量函数.基于偏移场校正的能量函数优点是对初始轮廓不敏感，缺点则是对严重灰度不均的图像分割效果不佳；基于局部区域的能量函数优点是对目标边界可进行精确分割，缺点则是容易陷入局部极小解.为克服两种能量函数的缺点，提升对灰度不均和噪声图像的分割鲁棒性，模型引入自适应权重函数构建能量泛函，并使用梯度下降法进行求解.

基于概率统计的具有代表性的是有限混合模型（FMM），FMM中常见的高斯混合模型（GMM）广泛应用于图像分割.文献[7]提出基于GMM 的分层改进算法和邻域信息约束算法，但对噪声鲁棒性不佳.SMM由于比GMM 具有更厚重的尾部，所以对噪声的鲁棒性更佳.这也是很多学者以SMM 为基础，提出改进算法的原因.文献[8]提出一种基于马尔可夫随机场(MRF)的SMM用于脑部MR图分割.该模型将原SMM中的先验概率替换为图像像素空间信息，并使用EM 算法进行求解.实验表明，引入基于MRF的像素先验概率联合分布在一定程度上能够克服噪声对图像分割的影响.文献[9]将SMM和水平集相结合，提出一种基于SMM 的快速鲁棒水平集分割方法.该方法构造了水平集函数和SMM 模型之间的交互反馈，通过惩罚项与均值的偏差来增强数据保真度，从而重写SMM 的成本函数，通过EM 进行求解.实验表明，该方法能够对不同类型的图像进行有效分割，具有一定的拓扑灵活性，但实验样本不含噪声，未能体现该方法的抗噪性.

为了解决上述方法中对噪声处理的不足之处，将Student’s t混合模型的t分布进行多分类，提出一种多分类SMM模型应用于高噪声图像分割.该模型在传统SMM的基础上进行多分类处理，将模型中的t分布再次进行混合重组，用新的SMM 代替t分布，利用t分布中的重尾特点和多重t分布混合重组克服图像中的噪声.通过对3 组不同样本：含有9%高斯噪声普通图像、含有9%椒盐噪声普通图像和含有9%噪声的脑MR仿真图进行分割实验，以精确度（Accuracy）、信噪比（SNR）和DICE作为评价指标，实验结果表明本研究方法优于其它方法.

1 模型原理

受文献[7]的启发，本文定义了一种多分类Student’s t 混合模型，并利用EM 算法进行求解，通过最大化后验概率实现高噪声图像分割.

1.1 Student’s t混合模型

假设图像X由N个像素点构成，表示为X=(x1，x2，…，xN)，Student’s t混合模型由K个t分布构成来对图像X进行描述，具体如下所示：

其中，Π =(π1，…，πk)，Θ =(Θ1，…，Θk)，πk为混合模型中第k个分量的权重，且满足如下条件：

t(xi|Θk)是像素xi属于第k个分量的概率密度函数，具体如式(3)和式(4)所示：

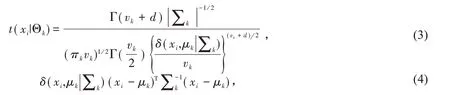
其中Γ为伽马函数，Θk={μk，∑k，vk}代表第k个t分布的均值、协方差和自由度.

1.2 多分类Student’s t混合模型

为了降低噪声和灰度不均对分割结果的影响，将传统Student’s t混合模型中的t分布再次进行分类处理.使用新的Student’s t混合模型对t分布进行重新建模，即用Student’s t混合模型代替第kj个t分布.使用多分类Student’s t混合模型对图像X进行建模，假设图像X由N个像素点构成，被分为K个不同类别，且每个类别由R个t分布构成.具体表示为式(5)：

其中，t(xi|Θjr)为t分布，参数集∏={πij，j=1，2…，K，i=1，2…，N}，πij表示像素点xi隶属第j个类别的先验概率，ηjr表示此像素点隶属第j个类别中第r个t分布的先验概率.参数集Θjk={μjr，∑jr，vjr，j=1，2…，K，r=1，2,…，R}.μjr，∑jr和vjr分别表示第j个类别中第r个t分布的均值、协方差和自由度.

根据式(5)，得到图像X的联合概率密度函数如式(6)所示：

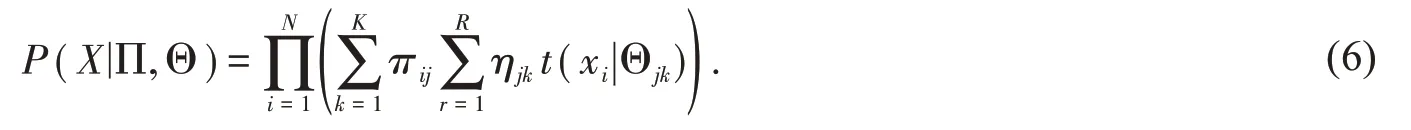
1.3 最大期望值算法（EM）求解

为了快速求解多分类Student’s t混合模型，引入最大期望值算法（EM）获取式(6)的对数似然函数如式(7)所示：

由于式(7)求解复杂，引入新变量ui简化多分类Student’s t混合模型求解，将模型中的t分布分解成伽马函数和高斯分布，具体如式(8)和式(9)所示：

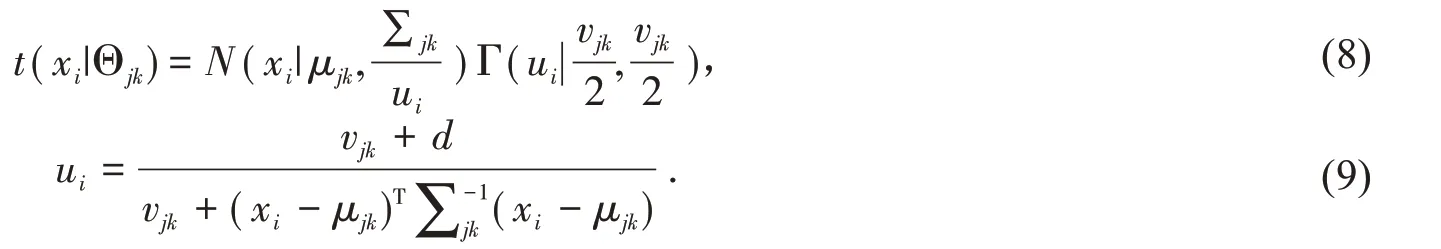
根据式(8)重新整理式(7)得到式(10)如下：

1.4 算法步骤

1)初始化图像类别数K和多分类t分布的类别数R、设定最大迭代次数T，自由度vjk，随机初始化πij、ηjr、μjr和∑jr，设置终止条件 1 ＜L(Π，Θ)t+1/L(Π，Θ)t＜1.001，其中t为迭代次数；

2)E步：根据式(9)和式(10)，计算ui、L(Π，Θ)；

3)M步：更新参数πij、ηjr、μjr、∑jr；

4)判断是否满足终止条件或达到最大迭代次数T，若满足，则获取最大化后验概率完成图像分割；若不满足，执行步骤2)直至模型收敛.

2 实验及分析

2.1 样本及评价指标

实验样本分3 类：1）含有9%高斯噪声的普通图像；2）含有9%椒盐噪声的普通图像；3）含有9%噪声仿真医学影像数据中的去颅骨脑部磁共振（MR）图.本研究方法多分类的Student’s t 混合模型MCSMM与k-means、GMM 和基于Dirichlet分布的Dgm[10]算法进行实验对比评价.评价图像分割结果的优劣，通常采用分割后图像与标准分割的相似度来进行评价.图像相似度评价指标有多种，本文选取精确度（Accuracy）和信噪比（SNR）作为评价指标，具体如式(11)和式(12)所示.

其中Nx和Ny分别是图像上行列像素个数，f(x，y)为待评价图像灰度，f(x，y)−g(x，y)为去噪后图像灰度.由式(11)和式(12)可知，Accuracy和SNR越高，表示分割精度越高，图像视觉效果更好.

由于医学图像脑MR 图的特殊性，另选取文献[11]中基于区域重叠的DICE 作为评价指标，具体如式(13)所示：

其中Sseg表示待评价分割结果，Sgt表示标准分割.正常脑组织划分为脑脊液（CSF）、灰质（GM）和白质（WM）.以DICE CSF、DICE GM 和DICE WM 分别代表分割后的脑脊液、灰质和白质与标准分割对应脑组织的重叠区域面积.DICE值越大代表相对应的脑组织重叠区域面积越大，分割结果越接近标准分割.

2.2 含有9%高斯噪声普通图像

图1为本研究方法多分类Student’s t混合模型（MCSMM）与k-means、GMM 算法分割含有9%高斯噪声普通图像的结果.其中图1a）为实验原图，b）为在实验原图上添加了9%高斯噪声的效果图，c）～e）分别为k-means、GMM 和MCSMM 的分割结果.表1为3 种算法在9%高斯噪声下精确度和信噪比的对比结果.由图1和表1可知，GMM 在含有大量高斯噪声的图像分割中，分割精度和信噪比表现较为不稳定，k-means虽然在多幅图像分割精度较为稳定，但是分割精度仍然较低.本文方法MCSMM在对含有大量高斯噪声图像进行分割时，表现良好.不但分割精度和信噪比得到了很大的提高，而且分割结果在视觉上表现更为理想.

图1 9%高斯噪声下分割结果Fig.1 Segmentation results with 9%Gaussian noise

表1 9%高斯噪声下分割定量对比Tab.1 Quantitative comparison of segmentation with 9%Gaussian noise

2.3 含有9%椒盐噪声普通图像

图2为本研究方法MCSMM 与k-means、GMM 算法分割含有9%椒盐噪声普通图像的结果.其中图2a）为实验原图，b）为含有9%椒盐噪声的图像，c）～e）分别为k-means、GMM 和MCSMM 的分割结果.表2为3种算法在9%椒盐噪声下的Accuracy和SNR对比结果.由图2和表2可知，GMM的分割精度和分割效果较差，k-means 算法在个别图像上的分割效果要优于GMM 算法.而MCSMM 由于对传统的Student’s t混合模型进行了分类处理，有着较强的抗噪性.对含有大量椒盐噪声的图像进行分割时，无论是分割精确度还是信噪比，比k-means和GMM都有了很大的提高.

图2 9%椒盐噪声下分割结果Fig.2 Segmentation results with 9%salt and pepper noise

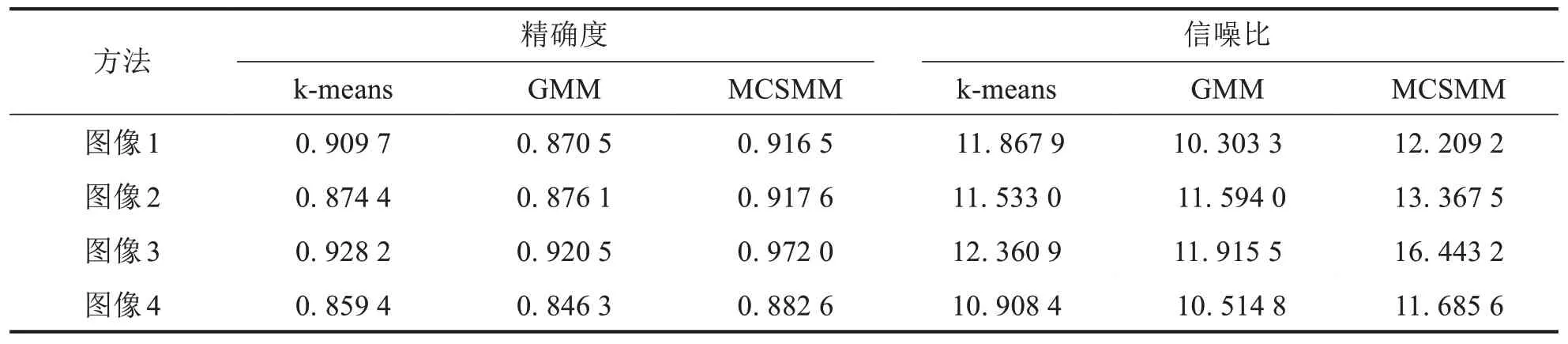
表2 9%椒盐噪声下定量对比Tab.2 Quantitative comparison of segmentation with 9%salt and pepper noise

2.4 含有9%噪声脑MR仿真图

图3为本研究方法MCSMM 与k−means、GMM、Dgm 算法分割含有9%噪声脑MR 仿真图的结果.其中图3a）为含噪声实验原图，b）标准分割，c）～f）分别为k−means、GMM、Dgm和MCSMM 的分割结果.表3～6为4种分割算法的Dice、精确度和信噪比3个指标对比.由图3和表3～6可知，Dgm的分割效果最差，对个别仿真图脑脊液的分割结果非常不理想.从DICE 指标看来，GMM 对脑脊液的分割略逊色于k−means，但是对白质和灰质的分割效果却明显优于k−means 算法.精确度和信噪比指标上，GMM 也优于k−means.本文方法MCSMM 采用了Student’s t混合模型，比GMM 具有更长的拖尾，在SMM 的基础上对其中的t分布进行再次分类，用新的Student’s t 混合模型代替t 分布，以达到更好的抗噪效果.从Accuracy 和SNR 指标可以看出，MCSMM 与GMM 相比，分割精度有了一定程度的提高，信噪比指标也优于GMM.从DICE 指标可以看出，MCSMM对脑脊液、灰质和白质的分割精度与其他3种方法相比均为最优.

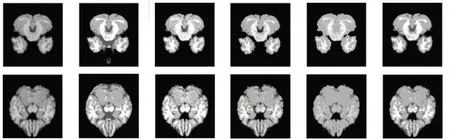
图3 9%噪声下脑部MR仿真图分割效果Fig.3 Segmentation effect of brain MR simulation image with 9%noise

表3 第40张仿真图9%噪声下分割定量对比Tab.3 Quantitative comparison of segmentation with 9% noise in the 40th

表4 第50张仿真图9%噪声下分割定量对比Tab.4 Quantitative comparison of segmentation with 9%noise in the 50th simulation image

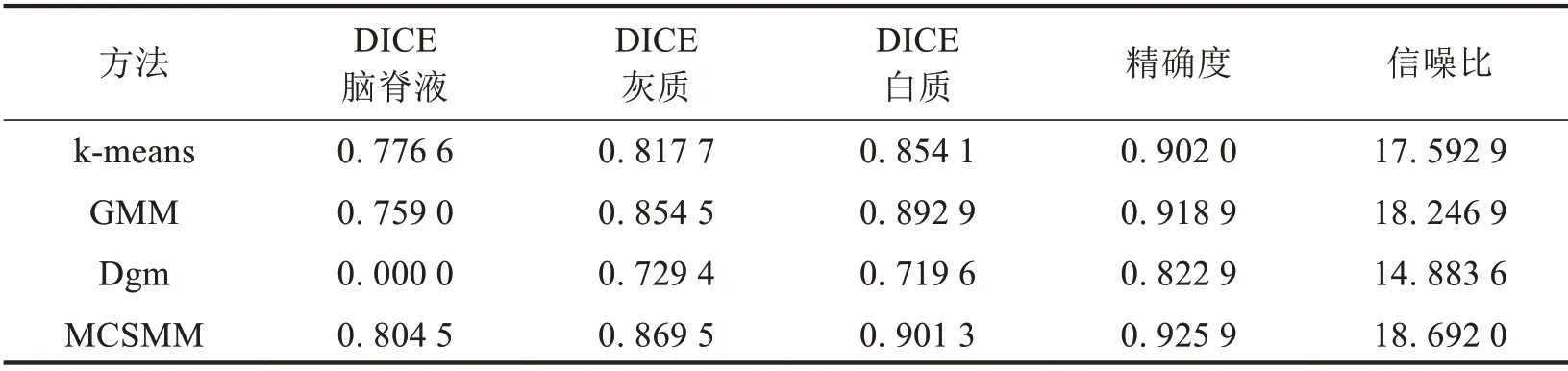
表5 第70张仿真图9%噪声下分割定量对比Tab.5 Quantitative comparison of segmentation with 9%noise in the 70th simulation image

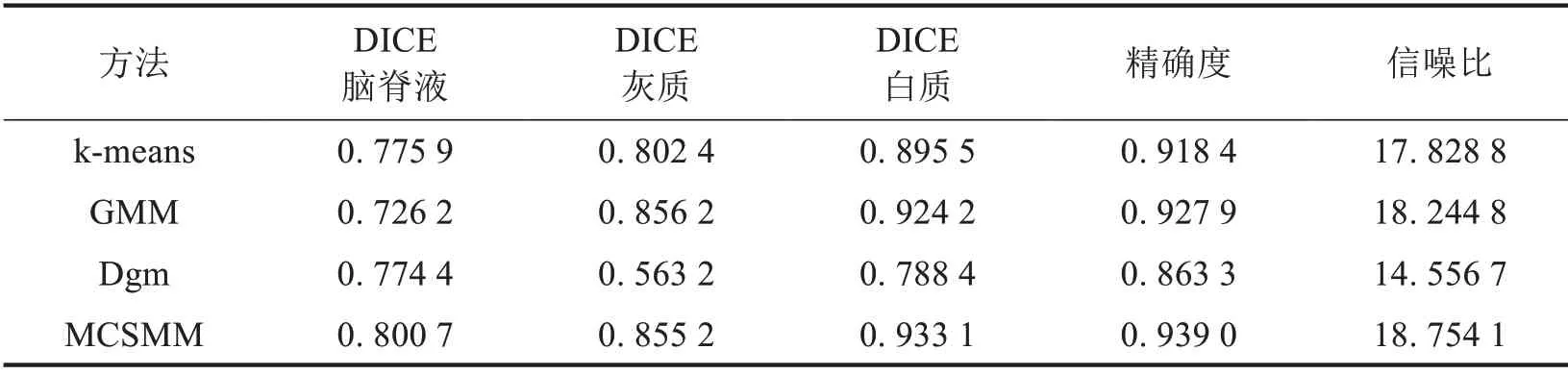
表6 第98张仿真图9%噪声下分割定量对比Tab.6 Quantitative comparison of segmentation with 9%noise in the 98th simulation image

3 结论

本研究针对高噪声图像提出一种基于多分类Student’s t混合模型的分割算法.该模型在SMM 的基础上引入多分类思想，将Student’s t混合模型中的t分布替换成Student’s t混合分布，利用多重t分布的厚尾特点，有效解决了高噪声图像分割时噪声敏感问题.实验表明，本研究方法与k−means、GMM 和Dgm 方法相比，在对含有不同类型噪声的图像进行分割时，都获得了更好的分割效果，分割效果图上的噪声点也更少.但本研究的不足之处在于未考虑像素点的邻域空间信息，因此在模型中加入像素空间约束，进一步提高模型的抗噪性和对偏移场的鲁棒性是下一步研究方向.