EP/MeTHPA/TAP 树脂体系固化动力学
2020-12-21杨浩黄文煜周栋张唯悦刘启抱
杨浩,黄文煜,周栋,张唯悦,刘启抱
(上海复合材料科技有限公司,上海 201114)
环氧树脂(EP)能够与多种固化剂反应形成三维网络结构[1],是一种理化性能优异且稳定的热固性材料,被广泛应用于国民经济的各个领域[2]。TDE–85 EP 官能度为3,分子结构单元中含有2 个缩水甘油酯基和1 个脂环族环氧基,具有反应活性高、黏度低、力学性能优异以及工艺性好等优势[3],其常与酸酐固化剂组合以液体成型的方式生产碳纤维增强复合材料并运用于航天产品[4]。为了对科研生产提供理论支持,笔者对EP/甲基四氢苯酐(MeTHPA)/2,4,6-三(二甲胺基甲基)苯酚(TAP)树脂体系进行了非等温固化动力学研究。
对于组分及配比恒定不变的EP 体系,其固化反应动力学进程会在较大程度上影响到最终固化物三维交联网络的形成以及其拓扑结构[5],从而影响到最终树脂产品的性能。对热固性树脂固化反应动力学的研究有助于理解其对应的固化反应机理、反应条件、网络结构与性能之间的相互关系,可为后续树脂配方的设计、固化工艺的选取、成型方式优化以及在实际过程中的运用提供重要的指导[6],以达到优化最终使用性能的目的。
1 实验部分
1.1 原材料
EP:TDE–85,工业级,天津晶东化学复合材料有限公司;
MeTHPA:工业级,上海华谊树脂有限公司;
TAP:工业级,上海华谊树脂有限公司。
1.2 仪器及设备
差示扫描量热(DSC)仪:NETZSCH DSC 204型,德国耐驰公司;
真空烘箱:DHG90000 型,杭州瑞佳精密科学仪器有限公司;
电动搅拌器:SN–OES–100SH 型,浙江力辰仪器科技有限公司。
1.3 试样制备
将EP,MeTHPA,TAP 按照质量比100 ∶140 ∶1称取混合倒入烧杯,之后用电动搅拌器将该树脂混合物于室温下搅拌10 min,使其混合均匀,最后将其置于–0.098 MPa 环境的真空烘箱中脱泡处理20 min 后备用。
1.4 性能测试
使用DSC 仪研究该树脂体系的非等温固化行为。称取5~10 mg 的样品放入坩埚,将坩埚密封放入仪器后进行升温扫描,参比坩埚为相同型号的空坩埚。该实验的测试条件为:四组不同升温速率(β):2,10,15,20 K/min,N2流 量 为50 mL/min,测试温度范围为25~200℃。
2 结果与讨论
2.1 DSC 分析
图1 为树脂体系的非等温DSC 曲线。

图1 EP/MeTHPA/TAP 体系非等温DSC 曲线
从图1 可看出,随着β 的提高,固化放热峰向更高的温度移动,这是由于β 增加使得树脂体系在低温下反应的时间缩短,需要通过更高的温度使其完成固化反应。从图1 还可看出,随着β 的提高,放热峰变窄,放热更加集中。固化特征温度见表1。
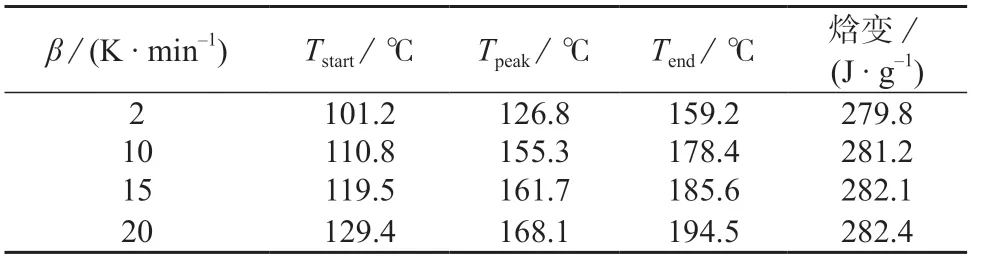
表1 EP/MeTHPA/TAP 体系DSC 特征温度
分析实验测试结果可得到EP/MeTHPA/TAP树脂体系不同β 下的固化度(α)与温度(T)见图2,α 与时间(t)关系图见图3。从图中可以看出,在同一温度下,β 越大,α 越小,曲线为类S 形曲线,即在反应起始阶段,α 增长较为缓慢,之后较快增长,再后来又变慢;从图3 可以看出,加快β 会使这些α曲线变得越来越陡峭,反应时间大大缩短。α 随着时间的增大而迅速增大除了与温度的上升有关外,还与体系自催化对反应的促进作用有一定的联系。反应后期,活性基团的浓度越来越低,交联密度不断增大,导致α 增长得越来越慢。
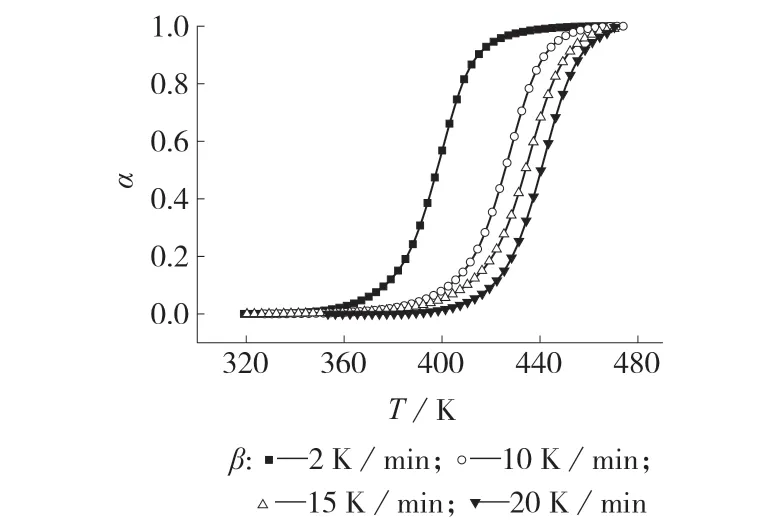
图2 EP/MeTHPA/TAP 体系α–T 曲线
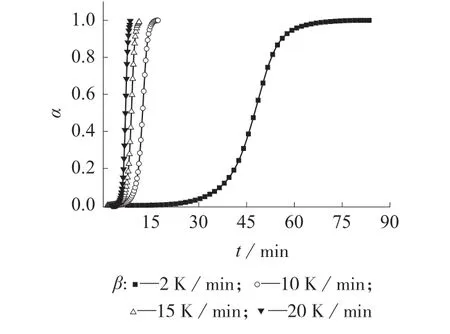
图3 EP/MeTHPA/TAP 体系α–t 曲线
2.2 固化动力学分析
(1)固化动力学方程提出。
DSC 反应动力学研究的基本假设是:反应热与反应基团的α 成正比[7–8]。为了求得反应速率dα/dt,可将α 对t 求导,如图4 为dα/dt 和α 关系曲线。
动力学三参数即指数前因子(A)、活化能(Eα)和动力学模型式f(α)之间互补性很强,换言之Eα的任何变化都将导致A 或f(α)向反方向变化,因此Eα可通过不同模型求解后取值,对于其它参数乃至整个模型的求解可采用Malek 法来实现。

图4 EP/MeTHPA/TAP 体系dα/dt–α 曲线
(2) Eα的求解。
为获得放热峰值温度(Tp)与β 的关系,采用Kissinger 法[9]等以ln(β/Tp2)对1/Tp作图,如图5所示,通过线性拟合可以获得离散点斜率,此斜率即为体系的Eα,求得结果为99.38 kJ/mol。
Ozawa 等认为固化放热峰值恒定不变[10],采用Ozawa 法以lnβ 对1/Tp作图见图6,求解Eα为99.36 kJ/mol。

图5 Kissinger 拟合曲线

图6 Ozawa 拟合曲线
若Eα在整个固化过程中不是一个常数,而是随着α 的变化而变化,利用等转化率法就能知道在整个固化过程中Eα的变化情况,方法之一就是Flynn-Wall-Ozawa 法。在不同α 下,以lnβ 对1/Ti(Ti为每个α 对应的温度)作图,如图7 所示,并对离散数据进行线性拟合,所得的斜率即为所求Eα,结果如图8 所示,其平均值为95.80 kJ/mol。
与Ozawa-Flynn-Wall 法类似Starink 法[11]为另一种等α 法求解Eα的一种方法。

图7 Ozawa-Flynn-Wall 法拟合曲线

图8 Ozawa-Flynn-Wall 法求解的不同α 的Eα
在 不 同α 下,以ln(β/Ti1.92)对1/Tα作 图,如图9 所示,并对数据进行线性拟合,所得的斜率即为所求Eα,结果如图10 所示,其平均值为87.79 kJ/mol。
据图8 和图10 看出,该体系Eα呈现逐渐增长的趋势,是因为固化反应过程中,树脂体系分子间发生交联,分子量增大,官能团的扩散位阻增大,需要吸收更多热量使反应进行。通过4 种方法计算出的Eα相差较小,笔者选择4 个值的中间值95.80 kJ/mol 作为后续固化动力学方程的重要参数。

图9 Starink 法拟合曲线

图10 Starink 法求解的不同α 的Eα
(3)固化动力学方程确定。
固化动力学方程是研究树脂固化反应过程的常见的数学模型,可以用来预测整个树脂体系的固化进程,是固化制度建立的重要依据,可为后续复合材料的成型提供理论支撑[12]。常用的Malek 法需通过定义构造函数y(α)[式(1)]和z(α)[式(2)]求解动力学模型f(α)和G(α)[13–14],其中:
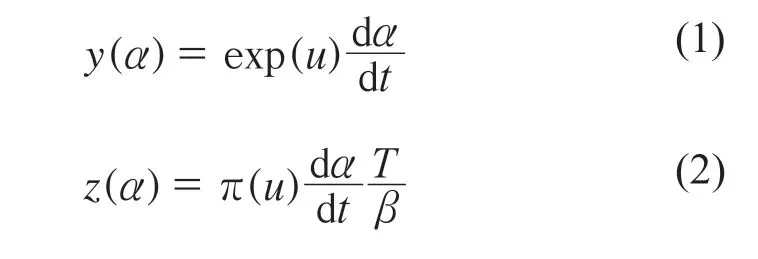
式中u 为约化活化能,其值等于Eα/RT,其中R 为普适气体常数8.314 J·(mol·K)–1。
π(u)为温度积分,常用Yang 和Senum 推导出的四阶有理式近似:

把实验数据代入式(1)、式(2),便可得到y(α)–α和z(α)–α 关系曲线。将其看做实验曲线。如果所得的实验曲线能够和标准曲线重叠,那么就可以认为该标准曲线所对应f(α)和G(α)就是所求的最概然动力学方程[15]。实验计算结果如图11 和图12所示。
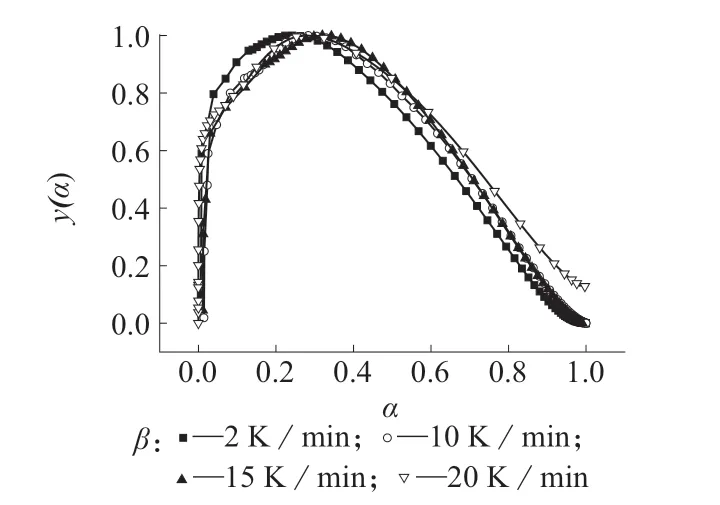
图11 y(α)–α 关系曲线
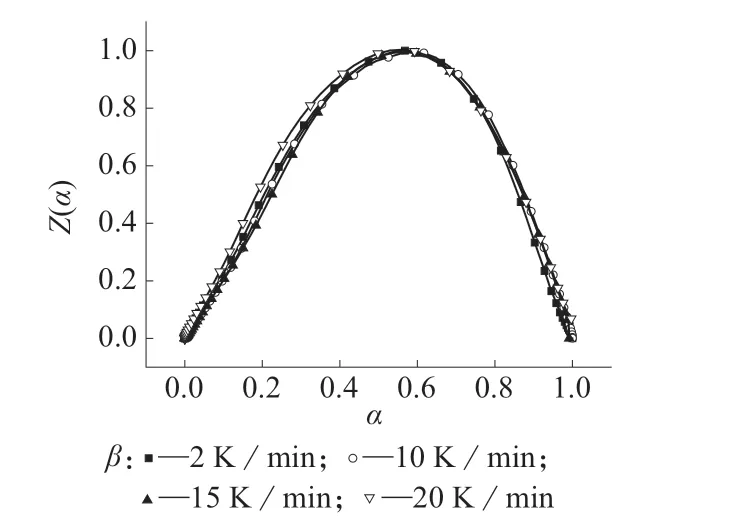
图12 z(a)–a 关系曲线
通过图11 和图12 的形状可以确定曲线y(α)和z(α)峰值所对应的α,分别为αM和αp∞,具体数值见表2。
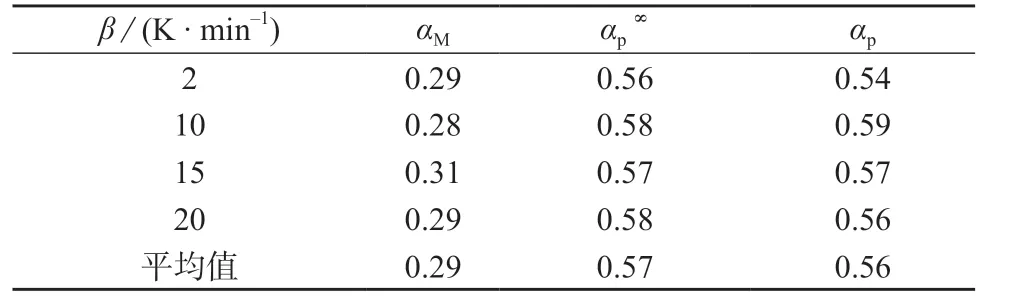
表2 EP/MeTHPA/TAP 体系α 参数表
分析表中数据可知αM远小于αp(DSC 曲线中最大放热峰值对应的α),并且αp∞的值也要小于0.632,根据Malek 法的分析标准,可通过双参数自催化模型SB(m,n)来求解动力学方程,如式(4):
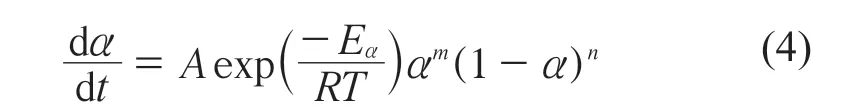
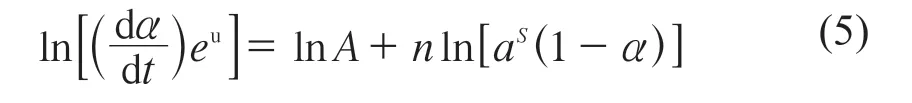
利用线性最小二乘法求得n,进而求得m,从而获得完整的速率方程。求解结果见图13,从图13可以得到相关固化动力学参数见表3。

图13 –ln[dα/dt×exp(u)]关系图

表3 EP/MeTHPA/TAP 体系动力学参数
将所求的m,n,lnA,Eα以及α,T,dα/dt 代入式(5)中即可得到固化反应速率方程,如式(6)所示,将实验值α 和T 代入该方程,便可求出拟合反应速率,将实验反应速率与拟合反应速率作图如图14 所示,从图14 可知,SB(m,n)模型可在较宽广的T 和α 范围内很好地描述EP/MeTHPA/TAP 体系动态升温条件下的固化反应速率。

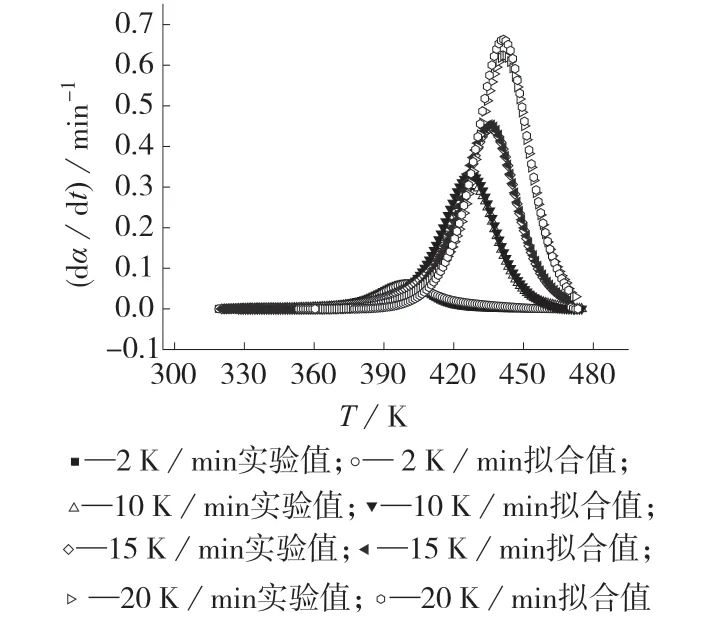
图14 模拟与实验对比图
3 结论
通过非等温DSC 法对EP/MeTHPA/TAP 体系进行了固化动力学研究,通过4 种方法计算出体系的活化能中间值95.80 kJ/mol。通过Malek 法求解了自催化固化动力学参数,最终确定了固化动力学方程
该模型计算得到的曲线能够很好地与实验曲线吻合,能够很好地模拟EP/MeTHPA/TAP 体系的固化过程。
