负刚度线性滞回阻尼减震效果分析与应用研究
2020-12-21彭凌云陈李光孙天威康迎杰
彭凌云, 陈李光, 孙天威, 康迎杰
(1.北京工业大学工程抗震与结构诊治北京市重点试验室, 北京 100124;2.清华大学土木工程系, 北京 100084)
消能减震技术通过在多个楼层布置耗能装置可以取得较为理想的减震效果,但阻尼器布置数量增加会大量占用建筑使用空间. 负刚度阻尼作为一种具有负刚度属性的新型消能减震技术,可以有效地解决上述问题.
近些年,一些学者提出半主动控制的拟负刚度阻尼系统,其中Iemura等[1-5]、史鹏飞等[6-8]和付杰等[9]、龚微等[10-11]、纪晗等[12-13]提出半主动控制的负刚度磁流变减震系统,并通过研究证明负刚度阻尼系统可以显著降低结构在地震中的加速度响应,并控制结构的位移,且相比于主动控制所需的能量较少,但相比于被动减震其稳定性和成本仍相对较高. 杨巧荣等[14-15]将负刚度阻尼与隔震技术结合应用在核电厂结构中,降低隔震层的加速度和位移,取得显著的减震效果.
线性滞回阻尼[16-17]作为一种应用在消能减震领域的滞回模型具有优良的耗能效果,但有可能增大结构的刚度,导致结构加速度响应增加. 具有负刚度属性的线性滞回阻尼可以有效弥补因结构刚度增加带来的不利影响,其耗能机制增加结构的阻尼水平,控制位移响应;但区别于黏滞阻尼,还具有降低结构刚度、形成力学上的隔震层的效果,进一步降低结构的加速度响应.
本文提出一种负刚度线性滞回阻尼减震系统(negative linear damping system,NLDS). 先通过平稳随机过程对负刚度减震机理进行理论分析,再基于SAP2000分析单质点模型在不同地震波下NLDS的减震效果. 最后将负刚度线性滞回阻尼布置于某火电厂的底层,分析其在实际结构中的减震效果.
1 负刚度线性滞回阻尼减震机理
1.1 负刚度线性滞回阻尼模型
提出一种滞回曲线如图1所示的负刚度线性滞回阻尼模型. 其特点为阻尼器在加载时随着位移的增加不提供或提供较小的阻尼力即加载刚度K≥0,在卸载时随着位移的增加阻尼力减小即K<0,形成一种负刚度效应. 将其布置在结构中可减小相应位置的刚度,并且消耗地震能量.
负刚度线性滞回阻尼模型可通过将复阻尼滞回模型与负刚度机制并联获得,即图1可由图2(a)(b)叠加得到,其中复阻尼模型可通过文献[18]中的阻尼器实现,属于位移型阻尼器;负刚度机制可通过文献[14]中的球铰预压弹簧机构实现,该装置力学性能稳定,通过改变预压弹簧的长度和刚度可以调整负刚度的大小,并且根据理论公式设计相应出力要求的负刚度装置,可以满足一般工程中对阻尼器的吨位需求,弹簧机构构造见图3. 将图3中铰机构中的弹簧替换为复阻尼器即可获得负刚度线性滞回阻尼模型.
1.2 理论分析
基于单自由度结构在平稳随机地面运动激励下的响应对负刚度线性滞回阻尼的减震机理加以分析. 单自由度结构的周期为0.8 s,阻尼比为0.05;将负刚度线性滞回阻尼加入单自由度体系中,并且通过减小结构刚度K和增大结构阻尼系数C予以考虑.
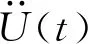
(1)
(2)
(3)
其模型参数取值为S0=0.148,ωm=8.77,ζm=0.71;S0为谱强度,ω和ζ分别为结构的自振频率和阻尼比;ωg和ζg分别为场地的特征频率和特征阻尼比;α2=ω/ωm,β2=ζ/ζm.
根据修正金井清谱公式计算考虑布置负刚度线性滞回阻尼后的结构位移和加速度响应标准差的变化.
图4(a)是负刚度比为0~50%变化时的结构频率和阻尼比的变化曲线;图4(b)是结构加入负刚度且增大阻尼系数C为原结构的1.5倍时的位移和加速度响应标准差的变化率曲线.
由此可知在结构中加入负刚度线性滞回阻尼后,结构的自振频率降低,周期延长,因此阻尼比增加. 通过提供一定的等效负刚度和附加阻尼,结构的加速度显著下降,位移也同样得到控制.
2 单自由度地震响应
2.1 基本参数
在原结构中加入线性滞回阻尼,基于SAP2000采用非线性直接积分的方式,对结构输入50条地震波,其中22条是近场波,28条是远场波.
结构模型如图5(a)所示,其中M为结构质量,K为结构刚度,C为结构阻尼系数. 为控制结构位移响应,负刚度线性滞回阻尼的等效刚度不能过小,因此在第1、3象限保留10%的正刚度,滞回模型如图5(b)所示. 在原结构基础上加入负刚度线性滞回阻尼,模型参数见表1. 其中Kl+Kn为加载刚度,Kl为卸载刚度,Kn为负刚度. 统计对比各地震波下结构位移及剪力响应的最大绝对值.
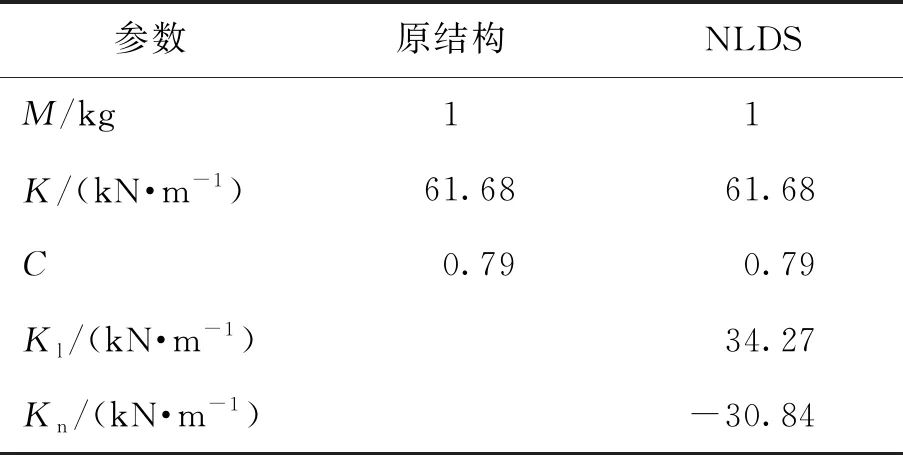
表1 结构参数
2.2 结果对比
图6是对单质点模型进行50条波输入下的地震响应统计结果. 由图可知,50条地震波作用下,结构位移的最大减震率达到49%,剪力的最大减震率达到47%;其中有48条波作用下,结构位移和剪力地震响应得到有效控制. 在32号和46号地震波作用下,结构中加入负刚度线性滞回阻尼放大了结构的剪力和位移响应.
2.3 负刚度阻尼放大结构响应的原因讨论
图7为32号地震波作用下的基底剪力和位移反应谱. 其中TO为原结构自振周期,TN为结构加入负刚度线性滞回阻尼后的结构自振周期. 由图可知,原结构自振周期刚好处于地震波频谱的极小值近附;加入负刚度线性滞回阻尼后,结构周期延长,反应谱值增加,因此基底剪力和位移响应增加.
综上所述,在原结构中加入负刚度线性滞回阻尼后,结构刚度下降,周期延长,在特定频谱的地震波作用下,结构本来处于响应较小位置,加入负刚度线性滞回阻尼后由于改变了结构的周期,结构的基底剪力和位移响应有增大的情形,但其反应绝对值仍保持较小数值. 从整体来看,负刚度线性滞回阻尼可以有效同时控制结构的位移和基底剪力响应幅值.
3 负刚度线性滞回阻尼应用分析
3.1 工程背景
选取某火电厂主厂房为分析对象,如图8所示. 该工程主体为6层钢框架结构,高47.3 m,横向(y向)3跨27.2 m,纵向(x向)9跨92 m;附属结构为钢结构框排架厂房,高32.9 m,横向(y向)4跨34.6 m,纵向(x向)9跨92 m. 该工程所处地区地震设防烈度为8度(0.3g)、场地类别为Ⅱ类;地面粗糙度为A类;厂房构件全部采用Q345b的型钢. 结构主要梁柱构件详细信息见表2.
针对火电厂结构横向(y向)进行单向地震波输入,分析并对比2种方案的减震效果.
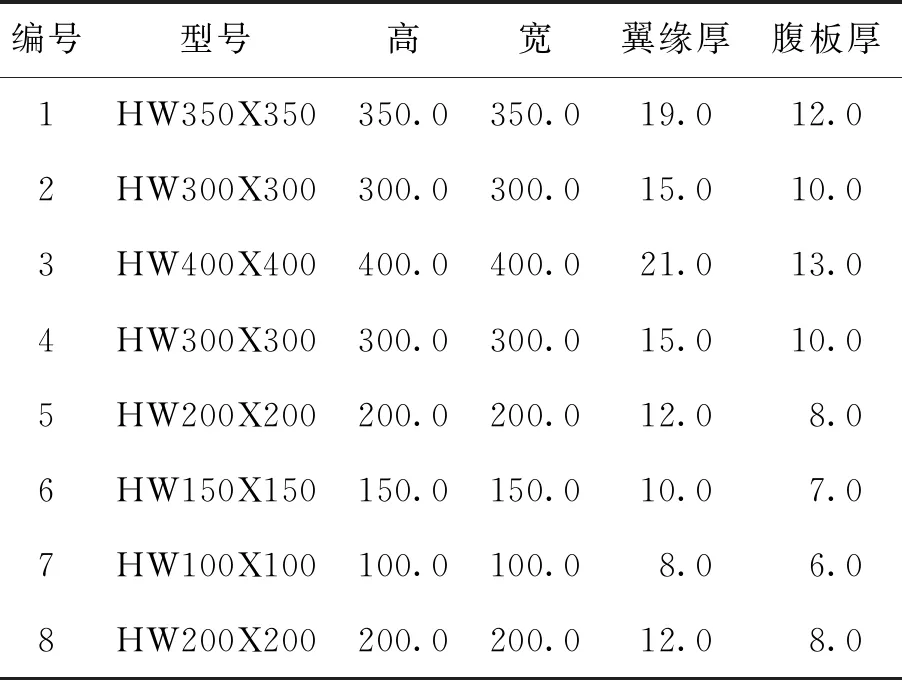
表2 梁柱截面尺寸
3.2 减震方案
1)屈曲约束支撑减震方案:在火电厂框架部分沿全高布置屈曲约束支撑,并且在排架底层同样布置屈曲约束支撑;其中结构x向布置48个,结构y向布置58个,总计10种共106个屈曲约束支撑,具体布置如图9所示.
屈曲约束支撑总屈服力为760 MN;底层布置屈曲约束支撑最大屈服力为9 500 kN. 结构中所布置的屈曲约束支撑具体参数见表3,其中L为支撑长度、S为核心截面面积、Ke为有效刚度、Fy为支撑屈服力.
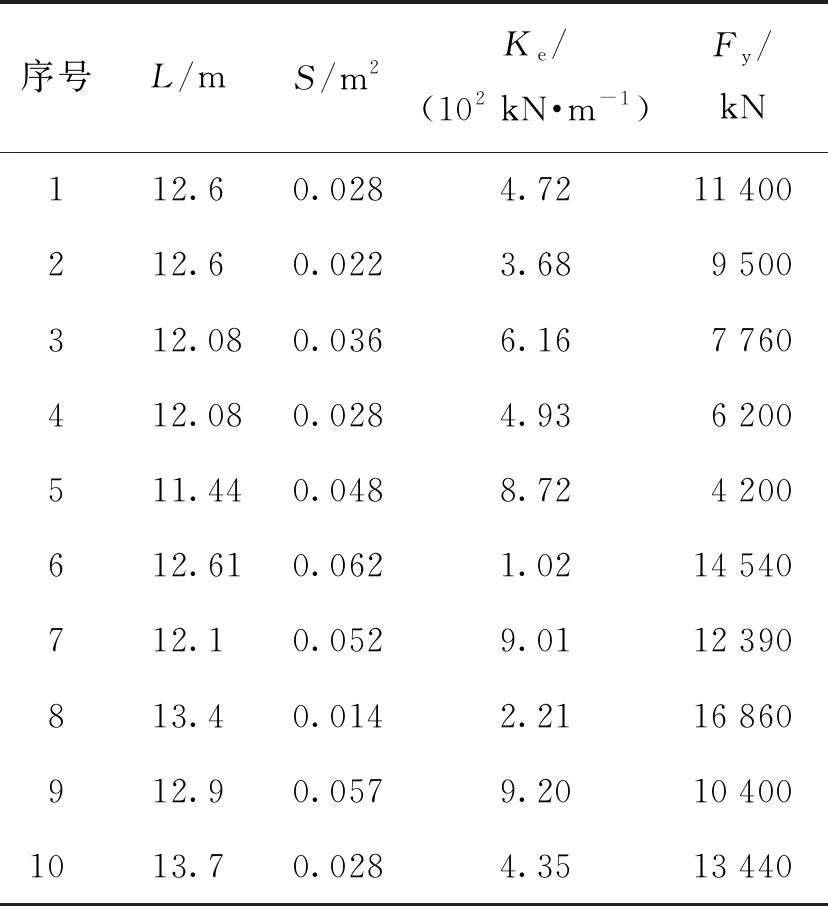
表3 屈曲约束支撑种类
2)负刚度线性滞回阻尼减震方案:只在火电厂厂房底层布置负刚度线性滞回阻尼器形成减震层. 其他层在结构纵向只保留边跨两榀框架支撑,去除结构上部纵向的其他屈曲约束支撑,见图10. 由于屈曲约束支撑可以提供较大的正刚度,为与屈曲约束支撑方案进行对比,需调整负刚度线性滞回阻尼的滞回曲线,使之在第1、3象限留有一定正刚度,避免结构刚度下降太多导致位移过大.
将负刚度线性滞回阻尼的卸载刚度Kl设置为与原屈曲约束支撑的加载刚度相同,在第1、3象限保留30%的加载刚度Kl+Kn. 减震层中布置的负刚度线性滞回阻尼器的最大屈服力为7 000 kN. 结构中的负刚度线性滞回模型见图11.
3.3 模态分析及地震波选取
基于SAP2000软件建立电厂钢结构主厂房的结构有限元模型,将负刚度线性滞回阻尼器通过Link单元进行模拟. 根据文献[20]所述方法,采用连接单元模拟负刚度线性滞回阻尼装置,滞回曲线如图11所示. 采用非线性时程分析方法,对该结构的屈曲约束支撑方案和负刚度线性滞回阻尼方案进行分析.
本文中采用割线刚度来进行模态分析,等效刚度计算原理如图12所示,其中KE为弹性刚度,Ky为屈服刚度. 将屈曲约束支撑的等效刚度设为弹性刚度,采用在多条地震波下计算位移响应平均值的方式计算阻尼器位移d. 根据Ke=Fy/d近似计算屈曲约束支撑的等效刚度. 负刚度线性滞回阻尼等效刚度图例计算取图12中Ke进行计算.
对比负刚度线性滞回阻尼方案与屈曲约束支撑方案的结构周期及振型见表4. 由此可知,通过加入负刚度线性滞回阻尼,结构周期延长.
时程分析选取3条地震波,分别为Nacanada波、Duzce波、Chi-Chi波,地震波归一化加速度时程如图13所示,加载时地震波峰值按400 cm/s2调幅. 地震波反应谱与规范反应谱如图14所示.
3.4 减震效果
为对比负刚度线性滞回阻尼与屈曲约束支撑的耗能能力,选取结构底层位置的阻尼器进行对比. 如图15所示,图中选取的阻尼器位于结构第10榀
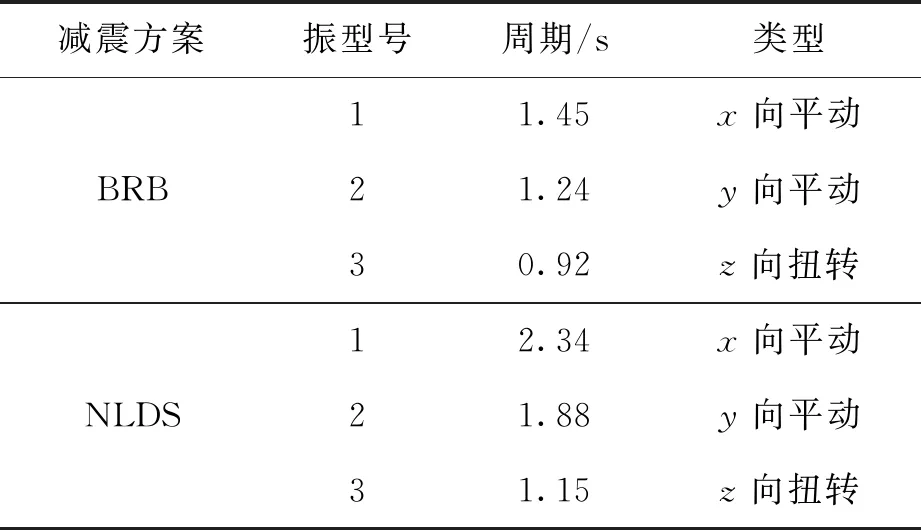
表4 结构基本信息
的第6根框架柱和第7根框架柱之间,该位置是结构在地震作用下相对变形较大处. 因而选取该位置处的阻尼器进行对比分析.
图16所示为上文所述位置处安装的屈曲约束支撑与负刚度线性滞回阻尼器在3条地震波作用下的滞回曲线. 相比于屈曲约束支撑方案,负刚度线性滞回阻尼方案的结构在Nacanada、Duzce、Chi-Chi 3条地震波下耗能分别提高14%、21%、25%. 由此可知,负刚度线性滞回阻尼在增加耗能的同时需要的阻尼力小于屈曲约束支撑.
图17所示为火电厂主厂房在3条地震波作用下输入的能量对比. 由此可知,相比于BRB方案, NLDS方案的结构由于刚度减小、结构变柔,输入结构的地震能量减少. 在Nacanada、Duzce、Chi-Chi三条地震波下结构能量输入分别降低30.7%、43.5%、48.2%,地震对结构的影响显著减小.
图18所示为火电厂主厂房在3条地震波作用下的基底剪力时程对比. 由此可知,相比于BRB方案, NLDS方案的结构地震全过程中基底剪力均减小. 在Nacanada、Duzce、Chi-Chi三条地震波下结构基底剪力分别降低37.6%、25.9%、15.4%,NLDS对结构基底剪力的控制效果显著.
图19所示为火电厂主厂房在3条地震波作用下主厂房各层层间位移角对比. 由此可知,相比于BRB方案, NLDS方案结构各个楼层层间位移角均减小. 在Nacanada、Duzce、Chi-Chi三条地震波下结构各层层间位移角分别降低53.8%、32.9%、30.4%,结构位移得到明显控制.
图20所示为火电厂主厂房减震层在3条地震波作用下楼层的滞回曲线. 由此可知,相比于原BRB减震方案,加入NLDS后,结构减震层等效刚度降低,滞回曲线更加饱满,耗能能力提高,结构底层的剪力峰值和位移均峰值均下降.
图21所示为3条波下结构减震层水平最大位移的时程曲线. 由此可知,负刚度线性滞回阻尼的加入使减震层的位移峰值减小;通过观察各个地震波下时程的峰点时间差,可看出结构周期有增大的趋势,具体延长幅度见表5. 因此,相比于屈曲约束支撑,负刚度线性滞回阻尼可以更有效地延长结构周期,并通过阻尼控制减震层位移.
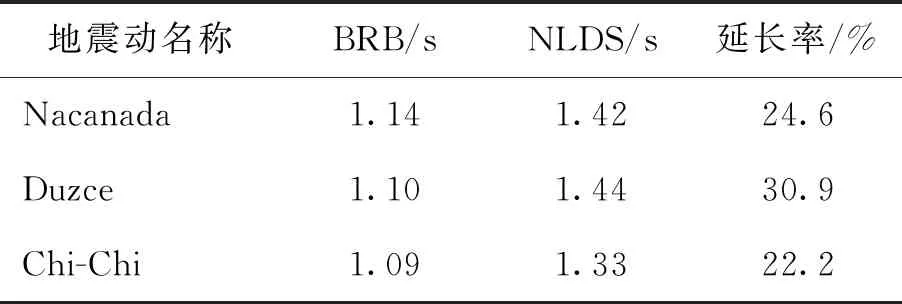
表5 周期变化趋势
4 结论
1) 负刚度线性滞回阻尼可以延长结构周期,提高结构阻尼比.
2) 与常规消能减震方案相比,在结构底层布置负刚度线性滞回阻尼装置并去除结构上部原有阻尼装置,可以获得相近或更优的减震效果.
