自适应灰狼小波去噪法在变压器套管引线超声检测中的应用

何海峰，罗宇昆，涂 斌，吴肖锋，李 顺，王 淦，王 昕

(1.国网四川省电力公司 广安供电公司，广安 638000；2.上海交通大学 电工与电子技术中心，上海 200240)

随着我国电力行业的快速发展，对变压器的可靠性提出了更高的要求。变压器套管作为重要的保护装置，其运行中需长时间受电、热等因素的影响，套管下引线端部夹铜铝过渡处受电动力或外力的影响易发生形变，甚至导致引线断裂，假若不及时排除故障，会影响变压器的稳定运行[1]。

现阶段变压器套管的检测方法主要有局部放电检测[2]、高压介损检测[3]、红外检测[4]等，上述方法仅能对变压器套管外部绝缘陶瓷进行结构检测，而难以判断套管内部引线的运行状态。超声检测技术作为一种新型检测方法，因具有较强的穿透性、无损性、非接触性[5]，在固体形变与裂纹检测中应用广泛[6]。因此，可通过以超声测距为基础的超声检测技术实现变压器套管内部引线的在线非接触检测。

超声检测时，回波信号中会携带大量结构及材料故障信息，故可通过分析回波来实现目标缺陷的检测。但回波在不同介质中传播时，会产生一定程度的信号衰减而变得微弱。此外，随机噪声也会对回波信号的采集产生影响，影响检测精度。因此，在对回波信号进行分析之前，可通过多种手段进行信号降噪。近年来，SURE阈值小波去噪法和自适应小波去噪法在非平稳信号去噪领域得到了较为广泛的应用[7-8]。但受限于超声信号自身的非平稳性，当干扰噪声在频带上与有用信息重叠时，上述方法的去噪能力较差且效率低，低幅值噪声识别程度较差，容易使信号有效信息的辨识度下降。

针对上述算法的不足，提出了一种自适应灰狼阈值去噪法。首先，对信号进行多尺度小波分解，引入基于包含多阶连续导数的梯度下降自适应阈值法，以适应多变含噪信号；然后，确定最小梯度值目标函数，通过灰狼优化进行目标寻优，有效区分噪声与有效信息；最后，通过目标阈值完成信号去噪。通过仿真及实例验证可得：该算法在去噪的同时保留了信号起振位置等有效信息，去噪效率较高，提高了信号的信噪比与均值误差，增强了信号的信息辨识度。在变压器套管引线的超声检测中，该算法可提高超声检测的精度，获取引线状态，具有一定的实用性。

1 超声检测法

1.1 超声检测原理

待测的变压器套管壁是由陶瓷构成的，厚度约为24 mm，瓷套管内充满变压器绝缘油，在套管的正中心位置穿过导电铜杆，铜杆外包绝缘纸，铜杆直径约为13 mm，内部引线与套管外壁表面距离约为66 mm。

在进行超声检测时，采用收发一体的超声探头，将超声探头依次置于变压器套管端部外壁A、B、C 3个位置，探头垂直于套管壁，并在两者之间涂抹耦合剂，套管的超声检测原理示意如图1所示。

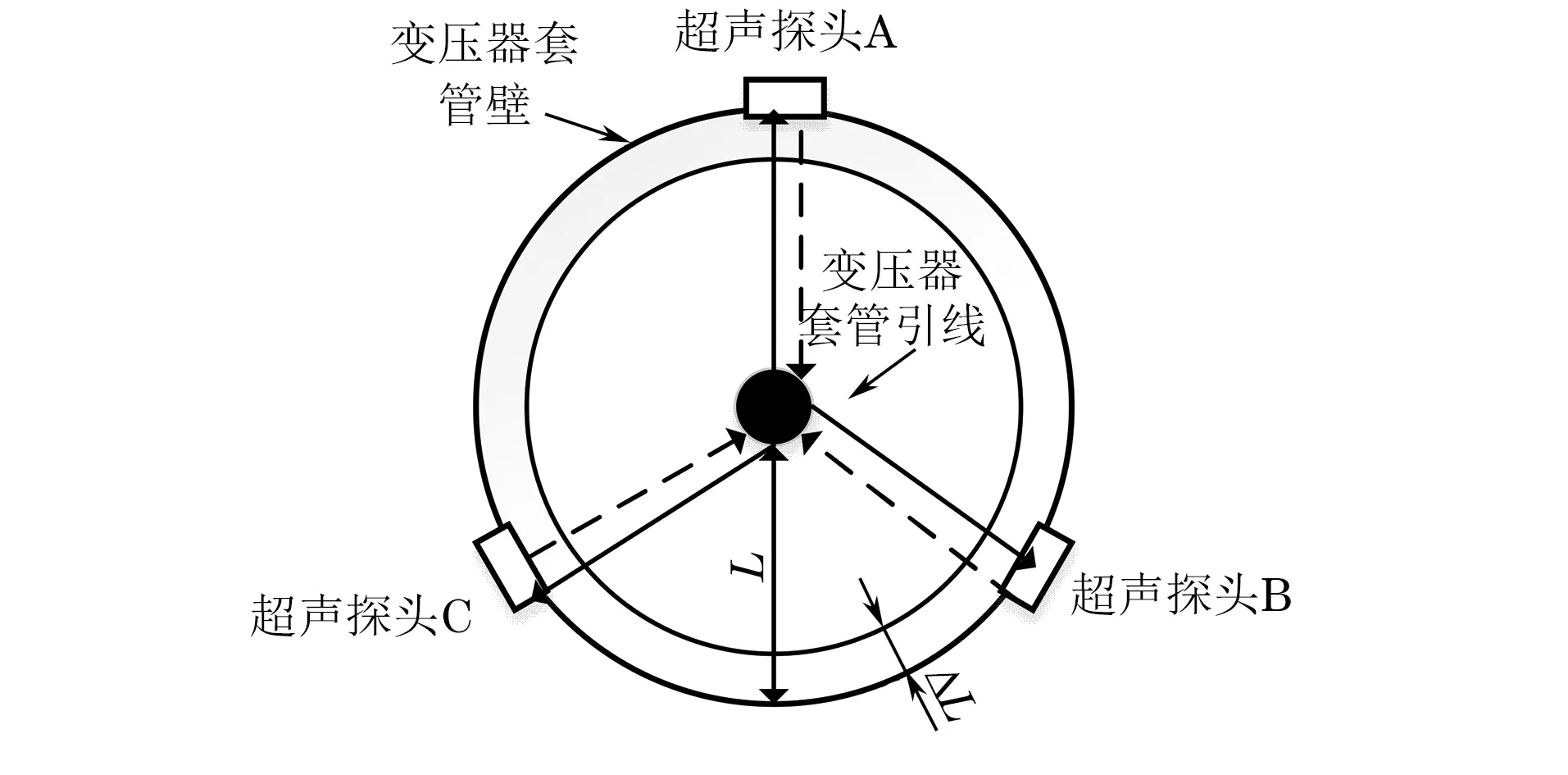
图1 套管的超声检测原理示意

由于4组超声回波信号均需经过套管陶瓷绝缘，对信号的传输产生相同的衰减作用，因此，在试验中不考虑超声波在变压器套管陶瓷壁中的传播对检测精度的影响。通过测量超声信号的飞行时间，根据超声波在绝缘油中的传播速度，可计算出引线与变压器套管之间的距离，实现变压器套管引线的状态检测。若3组测距结果相似，可认为变压器套管引线状态良好；若3组测距结果存在较大偏差，则变压器套管引线可能出现故障，需进一步进行检测。

1.2 信号分析

超声波作为一种非平稳时变信号，在不同介质中传播时，由于不同媒介间的声阻抗相异，在介质间界面处会产生反射回波，其中底面回波、缺陷回波与材料散射回波是回波的主要形式。

由超声探头发出的激励信号需2次经过变压器套管外壁及变压器油。从组成来看，套管陶瓷外壁是由尺寸较大的固体颗粒物构成的非均匀介质；而绝缘油的成分较为复杂，由不同种类、大小不一的颗粒物构成。当超声回波信号在传输过程中遇到不同类别的散射粒子时，会产生较为复杂的散射衰减，信号能量损失较大，此外，变压器油中的气泡数量和大小也会对超声信号产生一定的衰减效果。此时，回波信号极为微弱，需通过高灵敏度传感器进行信号采集。

但在采集微弱的回波信号过程中存在各种各样的噪声，如周围环境中的电磁噪声、电子元器件使用过程中的噪声以及周围环境中的随机白噪声等。通常，可通过硬件设备对较为明显的噪声信号进行滤除，但对于一部分近似于回波信号的噪声及小幅值噪声信号的去噪能力有限。因此，需通过软件手段识别较为复杂的噪声信号。

2 自适应最优阈值原理

对染噪(原始信号被噪声污染)超声回波信号分析发现，噪声主要是由与超声波信号无关的白噪声构成。假若染噪超声回波信号的观测值Y=[y0,y1,…,yi,…,yN-1]T,真实信号可表示为e=[e1,e2,…,ei,…,eN-1]T,则实测超声回波信号如式(1)所示。

yi=ei+ni,i=0,1,2,…,N-1

(1)

式中：ni为独立分布的高斯白噪声。

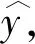
自适应小波阈值估计采用梯度下降法，下一刻阈值λ(m+1)等于此时阈值λ(m)加上负的均方误差函数的梯度值Δλ(m)，如式(2)所示。

λ(m+1)=λ(m)-μΔλ(m)

(2)

式中:μ为步长;Δλ(m)取值如式(3)所示。

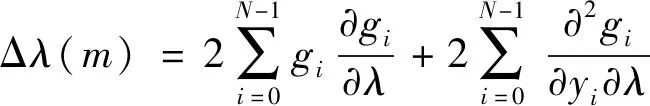
(3)

式中:gi为函数估计表达式，如式(4)所示。

gk=η(dj,k,λ)-dj,k

(4)

式中:η(dj,k,λ)为阈值函数;dj,k为j尺度上的小波系数。

使用硬阈值及软阈值函数作为阈值函数时，由于高阶导数不连续，难以实现自适应迭代，只能估计阈值大小，无法确定最优阈值。

因此，引进Sigmoid函数作为阈值函数[9]，该函数在小波系数大于所取阈值时，阈值函数近似于标准软阈值函数，该阈值函数如式(5)所示。

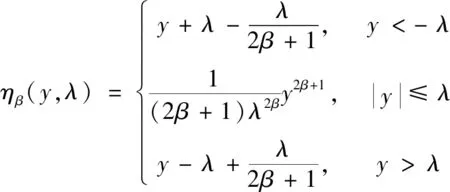
(5)

式中:β为正整数，取值为2。

求其一阶导数与二阶导数，分别代入式(3)、(4)中，经小波自适应阈值计算可得最优小波阈值。

3 自适应灰狼阈值去噪法

3.1 灰狼算法

灰狼算法(Grey Wolf Optimization,GWO)是一种受狼群捕食行为启发而提出的新型智能优化算法，其基本思想是狼群社会组织层级领导机制和群体捕食行为。灰狼等级按适应度分为首领狼α、副首领狼ρ、普通狼δ以及底层狼ω，其中α狼适应度最高，数量最少，负责指定狼群移动方向；ρ狼和δ狼适应度依次降低，负责辅佐α狼；ω狼适应度最低，数量最多，负责给α、β、δ狼提供信息[10]。

狼群在发动攻击之前，需要先根据式(6)、(7)包围猎物。

D=|C.Xp(t)-X(t)|

(6)

X(t+1)=Xp(t)-A.D

(7)

式中:t为当前迭代次数;Xp(t)为猎物的位置向量;X(t)为灰狼个体的位置向量,C=2r1，为摆动因子；A=2ar2-a，为收敛因子，r1、r2为取值为[0,1]的随机数；a的值呈线性变化，随迭代次数的增加从2衰减至0。

狼群成功包围猎物之后，由于α、β、δ狼的适应度最高，最靠近猎物，将由其判断猎物所在方位。

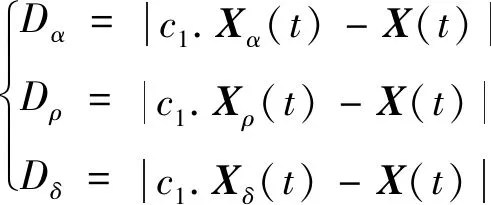
(8)

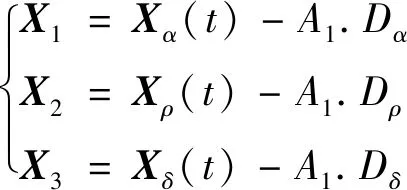
(9)

狼群的位置最终由α、β、δ狼共同决定。

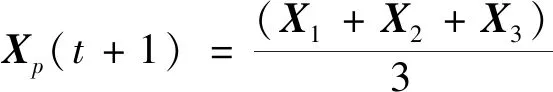
(10)

3.2 算法实现

(1) 设定GWO算法狼群数量、搜索空间维度、最大迭代次数、狼群初始地点向量，确定a、A、C，产生初始狼群。

(2) 根据式(2)确定狼群个体适应度，并进行比较，判断Δλ(m)值，当Δλ(m)最小时为最优值。将适应度函数为寻优依据，当前最好的3个个体位置作为初始狼群的α、β、δ狼位置。

(3) 依据α、β、δ狼的信息主导搜索方向，由式(8)、(9)实现α、ρ、δ狼迭代的位置转换，最终依据式(10)更新狼群的最新位置。

(4) 保存适应度最佳个体位置并不断进行迭代操作，实现狼群位置的更新。

(5) 判断GWO算法是否满足终止条件，若满足则输出最优阈值λGWO，否则转入式(2)。

针对超声回波信号的近似正弦分布的特性，使用sym6小波基进行6层小波分解。WFOTE算法的参数设定如下：狼群数量S=100，最大迭代次数Tmax=150,优化参数个数dim=1，上届lb=1，下届Ub=0.1。自适应灰狼阈值去噪法(Adaptive gray wolf threshold denoising，WFOTE)算法流程如图2所示。

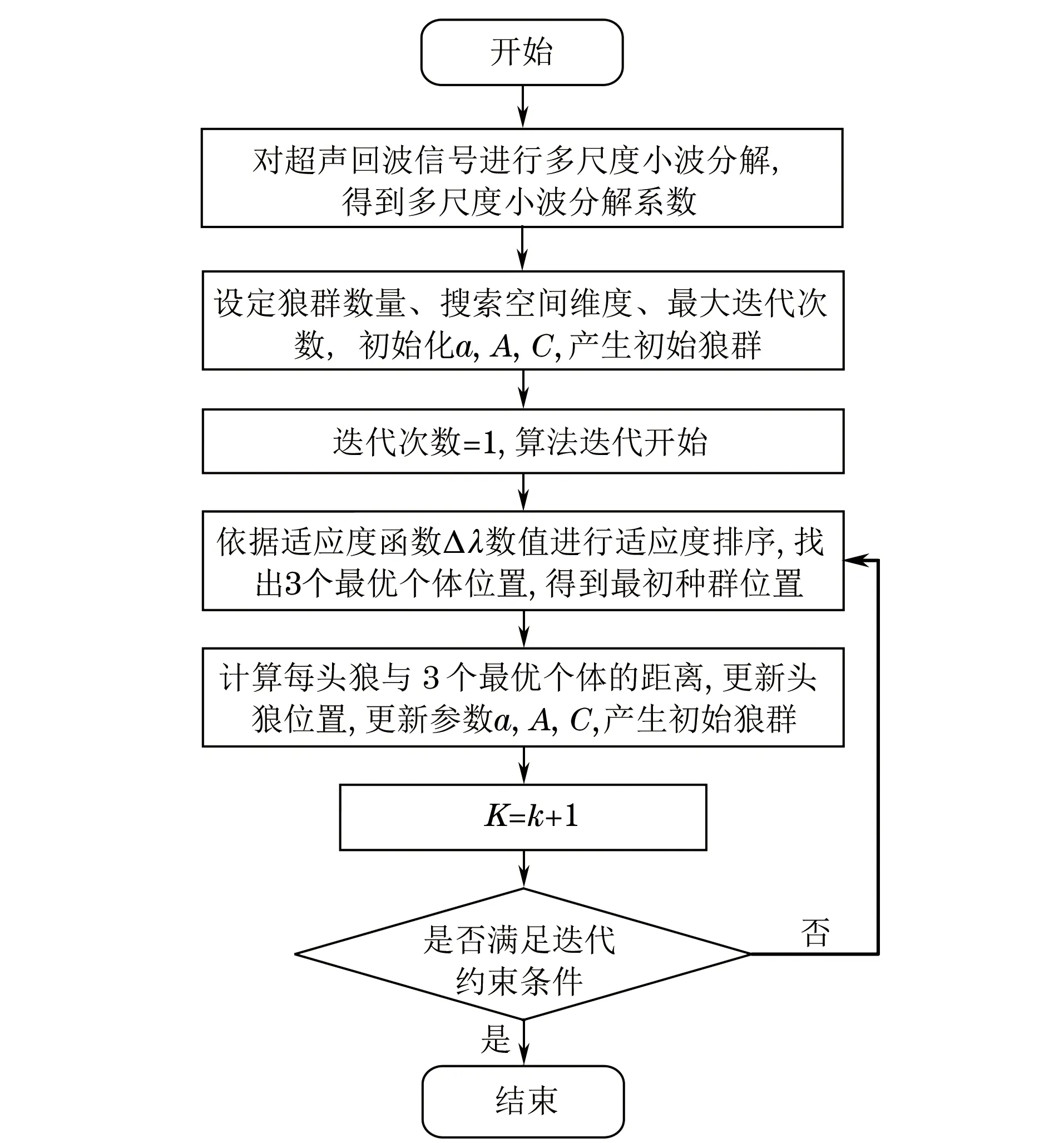
图2 WFOTE算法流程图

4 仿真分析与试验验证

为验证算法的去噪效果，引入小波自适应阈值法(Adaptive Wavelet Threshold Estimation，ATE)及粒子群算法优化小波自适应阈值法(Particle Swarm Optimization Adaptive Wavelet Threshold Estimation，PSOTE)进行对比。将信号信噪比(SNR)、均值误差(STD)与算法运行时间作为评判标准。

4.1 仿真分析

在窄脉冲超声检测中，依据超声回波信号的物理特性，超声换能器接收到的回波信号可模拟成高斯信号，如式(11)所示。

y(θ,t)=Aexp[-a(t-τ)]cos[2πfc(t-τ)]+θ

(11)

式中:a为带宽;τ为到达时间;fc为中心频率;θ为相位;A为幅度系数。

仿真原始信号如图3所示。

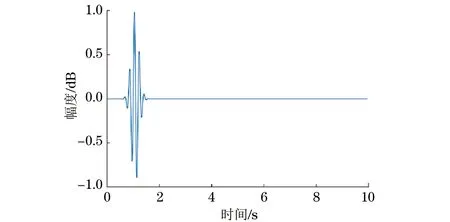
图3 超声回波仿真信号

对原始超声回波信号添加能量为2.82 dB的白噪声，得到染噪仿真信号,如图4所示。

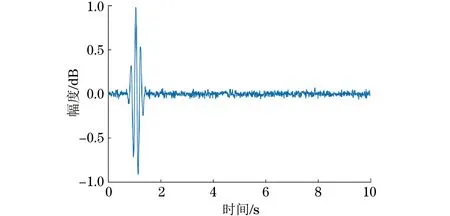
图4 染噪仿真信号

分别采用ATE去噪法、PSOTE去噪法及WFOTE去噪法进行去噪处理，结果如图5～7所示，信号信噪比及均值误差如表1所示。

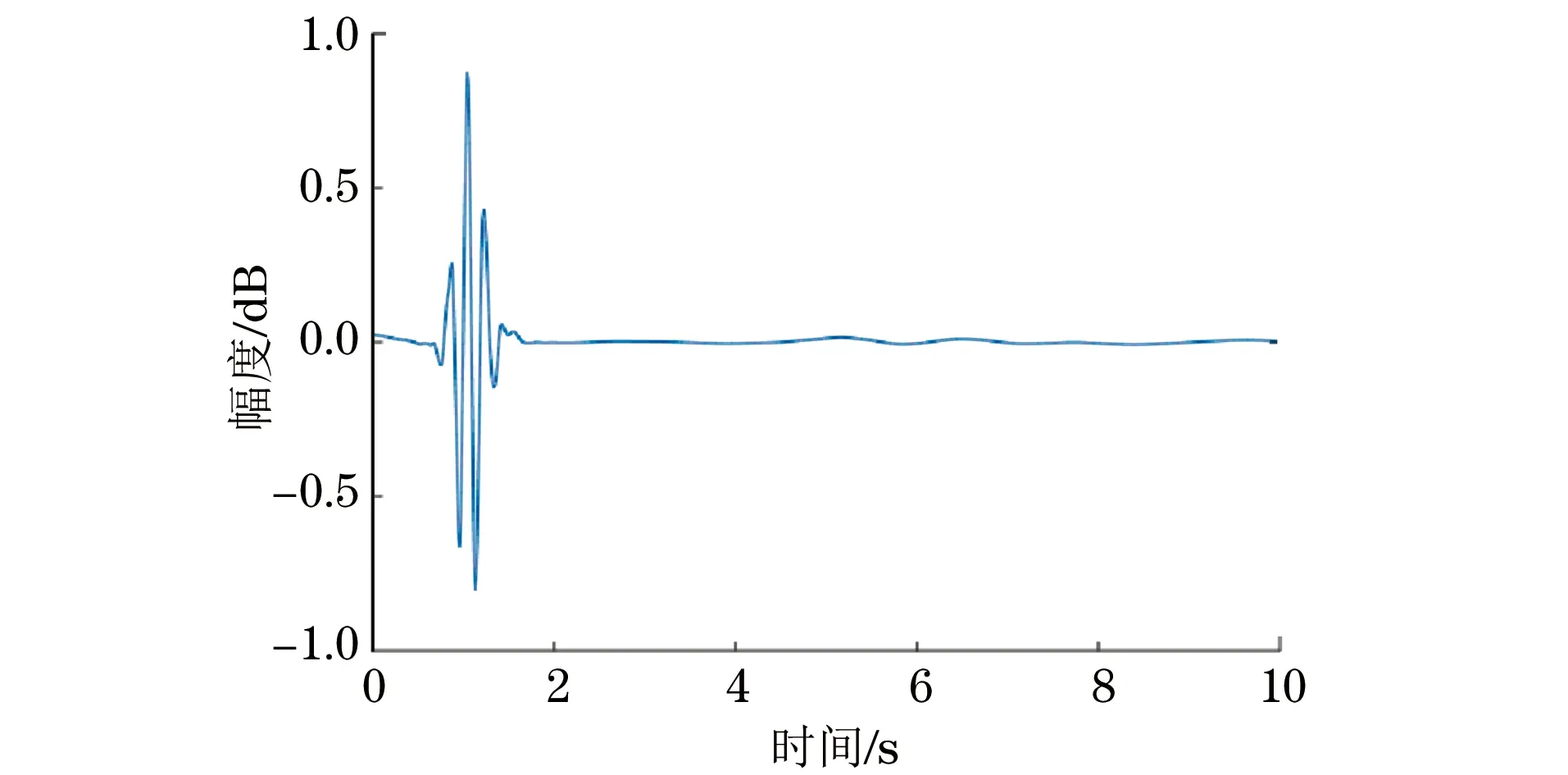
图5 ATE去噪后信号

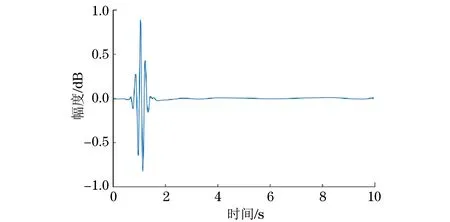
图6 POSTE去噪后信号

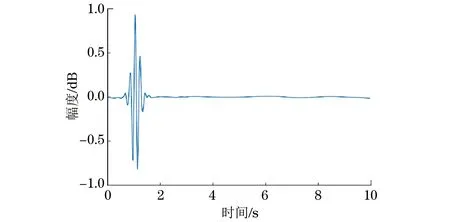
图7 WFOTE去噪后信号

表1 3种去噪方法的去噪效果对比

由上述结果可得，ATE法去噪后信号信噪比最低，均值误差最大，回波信号的起振位置基本被滤除，很难辨识并且信号波形不稳定，产生了一定程度的畸变，去噪效果最差；PSOTE法处理后，信噪比得到提高，均方值误差减小，超声回波信号起振位置虽保留下来，但信号相对原始信号产生了相应的畸变，去噪效果得到了进一步的优化，但并非最优;而WFOTE法处理后的信号信噪比最高，均方值误差最小，超声回波信号的起振位置不仅较为完整地保留了下来，信号畸变程度还最小，说明该方法的去噪效果最佳。为了进一步说明算法的去噪效果，统计了算法的运行时间(见表2)。

表2 3种去噪方法的计算时间 s

由表2可得，自适应灰狼阈值去噪法的运算时间最短，效率最高。为了进一步验证WFOTE法的去噪效果，对仿真信号分别添加能量为2.82,4.70,6.85,8.46 dB的白噪声，通过SNR与STD的变化趋势,检验去噪效果，结果如图8所示。

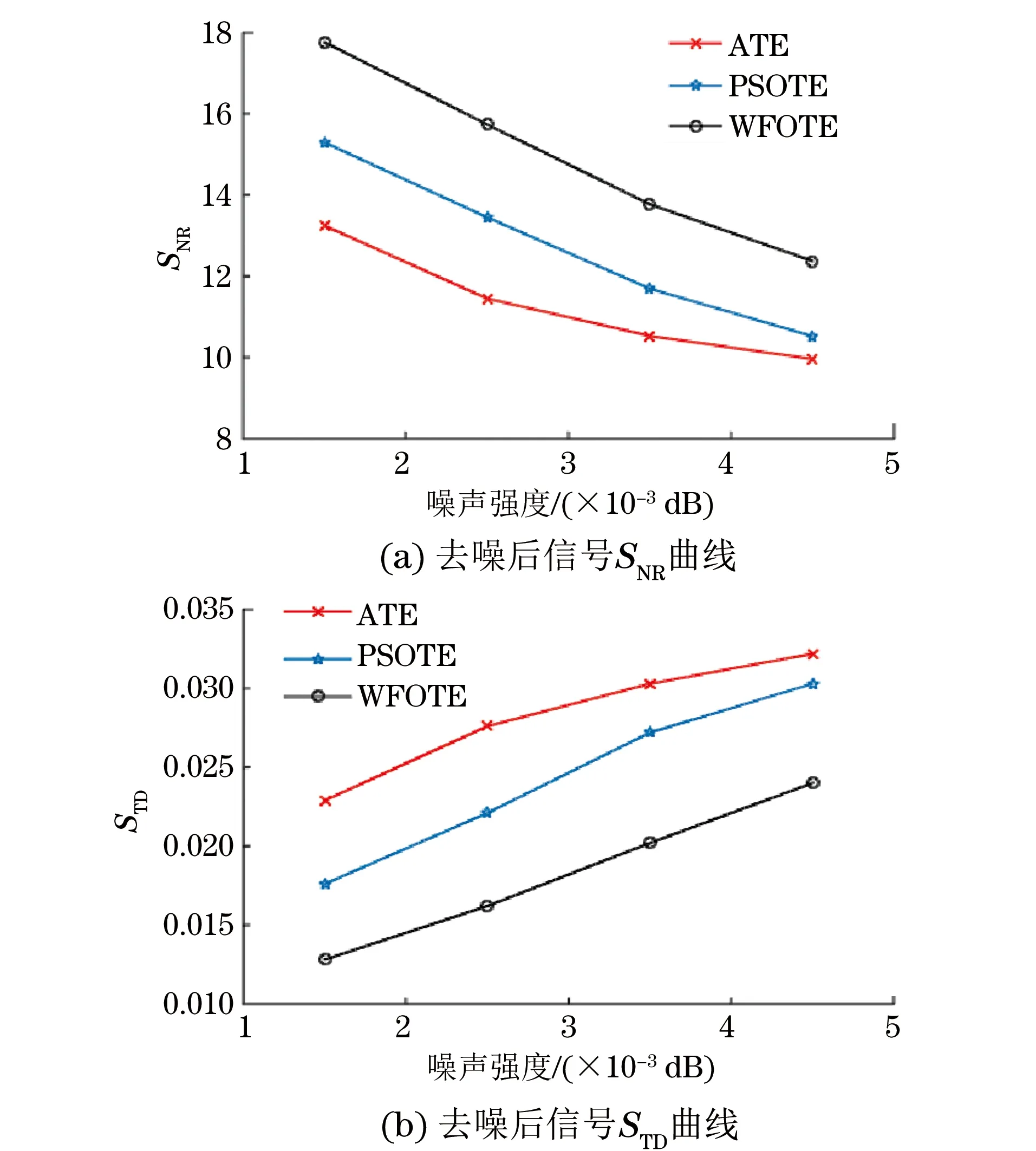
图8 去噪后信号的SNR与STD曲线

由图8可知，含有不同噪声强度的信号采用ATE、PSOTE及WFOTE法去噪后，信噪比随噪声强度的增大而逐渐减小，均值误差随噪声强度的增大而逐渐增大，但含噪信号经WFOTE法去噪后，信号的SNR最高，STD最低，去噪后信号的畸变程度最小，说明该去噪法的去噪效果最佳。

4.2 现场验证

为验证WFOTE算法的有效性，在四川省广安市杨公庙某110 kV变电站进行现场验证，选用一台110/35 kV的ABB变压器作为试验对象，选择B相高压套管进行超声检测。理论上，20 ℃时,超声波在变压器油中的传播速率为1.42 mm·μs-1。

用检测设备采集超声回波信号，如图9所示。经观察发现，该信号中包含大量的噪声，难以区分超声回波信号的起振等有效信息。因此，对该信号分别使用ATE、PSOTE、WFOTE三种方法进行去噪处理，考虑到回波信号的相似性，文中仅对一组信号进去处理，去噪结果如图10所示。

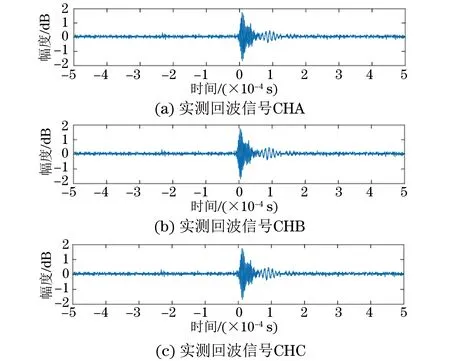
图9 现场采集的超声回波信号

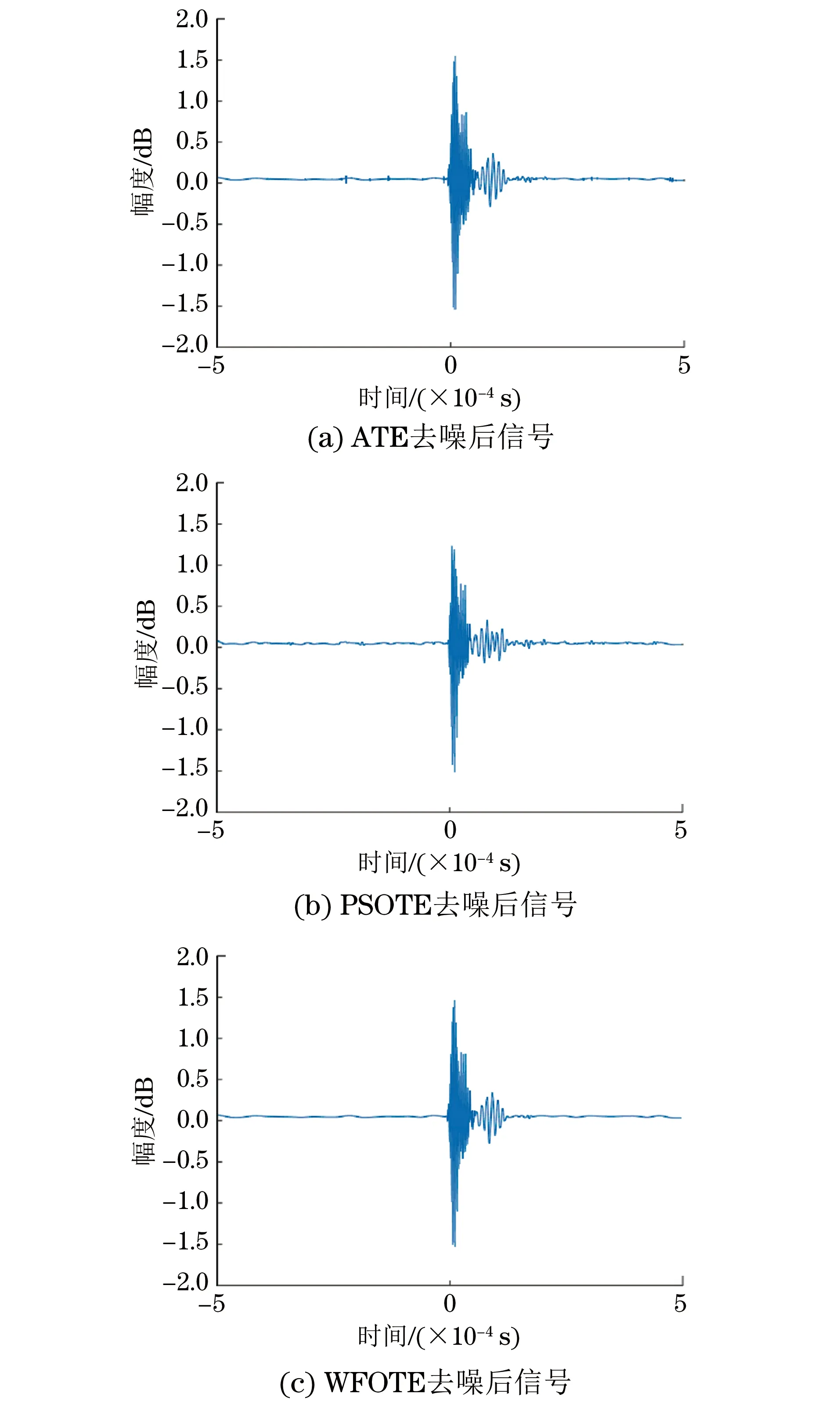
图10 实测信号去噪效果

从图10可以看出，采用ATE法去噪后的信号仍含有大量毛刺信号与噪声，这会影响超声检测的精度；采用PSOTE法去噪后效果较好，但回波信号波形不平缓，波形中仍含有部分毛刺信号，也不利于测量超声信号的飞行时间；而采用WFOTE法去噪后，回波信号的波形较为平缓，基本没有毛刺信号，波形起振位置等小幅值细节信息得以保留，去噪效果最好，更有利于识别信号中的有效信息。为了进一步检测去噪效果，信号信噪比、均值误差及算法的运行时间如表3所示。

由表3可知，经WFOTE法去噪后的信号SNR更高、STD更小，信号质量最佳；从算法运行时间上来看，WFOTE法去噪时间最短，去噪效率相较于其他两种算法高。

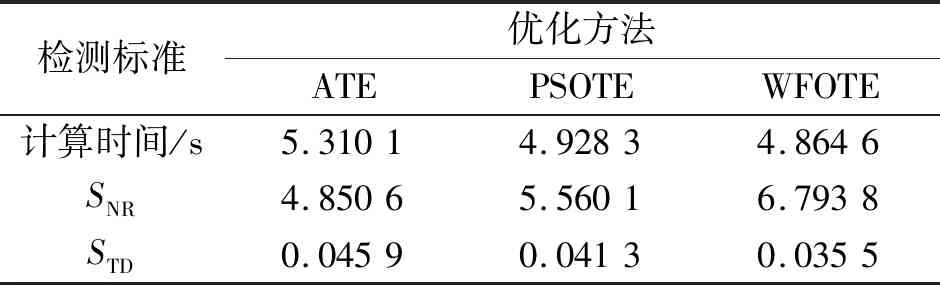
表3 3种实测信号的去噪效果

将WFOTE算法应用于其他两组信号中，根据超声检测结果进一步反应算法的有效性，得到的超声检测结果如表4所示。

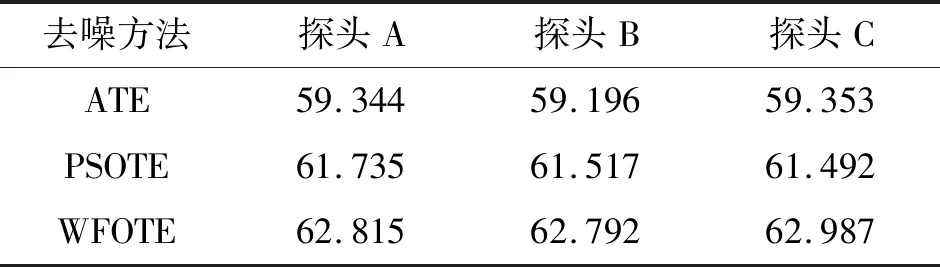
表4 3种方法去噪后的超声测距结果 mm

由表4可得，超声回波信号经WFOTE算法处理后，所得检测结果更接近于真实值66 mm，并且3组结果近似，彼此间数值差别不大，表明套管引线并无故障，符合实际情况。

因此，提出的WFOTE算法能更好地去除变压器套管引线超声检测过程中的噪声干扰，更好地传递回波信息，便于提高超声测距的精度，准确获取变压器套管引线的状态信息，效率更高，具有一定的实用性。

5 结论

(1) 通过基于梯度下降自适应阈值法，实现了小波阈值函数的选取，确定了梯度下降最小目标函数，通过灰狼优化算法，解决了传统自适应阈值去噪法寻优效果差的问题，减少了随机性，去噪效率更高。

(2) 对仿真及实测信号去噪，WFOTE算法在去噪的同时保留了回波信号起振位置等有效信息，波形平滑性最好，信号畸变程度最小，信噪比最高，均值误差最小，去噪效果最好。

(3) 通过现场验证，WFOTE算法更有利于获取超声回波中的有效信息，提高超声检测精度，更好地反映套管内引线的状态，具有一定的实用性。