三角波激励ECT测量电路
2020-12-18胡亚峰崔自强王化祥
马 敏,吴 轲,胡亚峰,崔自强,王化祥
(1.中国民航大学 电子信息与自动化学院,天津300300; 2.天津大学 电气信息与自动化工程学院,天津300072)
1 引 言
电容层析成像技术(electrical capacitance tomography, ECT)是近几十年发展起来的一种新型可视化检测技术,应用于多相流检测、流型辨识等,可以通过测量横截面的介电常数分布来确定材料分布情况[1]。与X射线、γ射线等传统的X线断层成像技术相比,ECT技术具有成本低、响应速度快、携带方便、无辐射、无侵入性、鲁棒性等优点[2~4]。
在提高ECT系统数据采集精度和速度方面的研究上,已有研究人员取得了相关成果。第一套实时ECT系统由曼彻斯特理工学院(UMIST)在1991年开发,他们研究对比了各种测量电路,如充电/放电电路、交流C/V转换电路、自平衡测量电路用于电容测量;在这些电路中,交流电路最适合ECT系统,它不受杂散电容和电荷注入的影响[5];赵进创等用激励信号幅值可控双模式交流型C/V转换电路实现微小电容检测,电路具有抗杂散电容能力,线性和分辨力良好且输出稳定[6];王雷等提出的微弱电容测量电路解决了电子开关电荷注入效应对测量分辨率的影响,可以达到较高的数据采集速率[7];高彦丽等分析设计了程控增益负反馈交流型电容测量电路来提高电路的测量范围和灵敏度[8];郑伟军等研制了一套基于DSP处理器和USB2.0技术的高速ECT数据采集系统[9];崔自强等提出了数字相敏解调与持零开关策略相结合的方法,改善了系统数据信噪比和采集速率[10];律德财等采用高压交流激励电路,验证了在370 V的激励电压下具有良好的灵敏度、分辨率等特性[11]。
目前,ECT系统均采用正弦波信号作为激励源,经过交流C/V转换电路,测量信息存储在输出的正弦波信号里,与激励信号同频同幅的正弦余弦信号作为参考信号,对输出的信号进行数字相敏解调,从中提取出电容信息[12]。数字相敏解调需占用大量的逻辑资源,且对数据处理速度要求高。本文提出的三角波作为激励信号,微分电路作为C/V转换电路的方法不需要对输出进行解调,节省了逻辑资源,且减少了电路的稳定时间,能提高系统的实时性。
2 方 法
ECT的测量原理为通过在电极施加激励电压信号,其它的电极作为测量电极连接到C/V转换电路将电容信号转换为电压信号。
2.1 电极激励

图1 ECT传感器结构模型图Fig.1 ECT sensor structure model
ECT成像系统由3个部分组成:电极阵列传感器、数据采集单元、图像重建单元。图1为常用的ECT传感器模型,外部的金属屏蔽罩接地可以降低外部噪声干扰。电极均匀分布在管壁,安装在电极之间的径向电极可以减少相邻电极之间的边缘效应。测量采用单激励的方式,首先通过在电极1上施加电压信号,2-N电极作为测量电极,然后对电极2施加激励信号,3-N电极测量。按此规律一直持续到第N-1个电极激励。对于N个电极的传感器,具有的独立测量值个数为N(N-1)/2[13]。
2.2 C/V转换电路设计
ECT测量的难点在于周围坏境的干扰太大,而传感器电极之间的电容值较微小。将微小的电容从杂散电容中提取出来的方法会影响ECT系统的成像精度。对于ECT的微小电容测量电路要求有:1) 抗杂散电容的能力强;2) 动态测量范围大;3) 响应速度快[14]。杂散电容主要来源有测量电极与屏蔽电极之间的电容、连接电极的屏蔽电缆的电容和电容测量电路中的COMS开关电容。总杂散电容约为150 pF,而测量电极对之间的电容范围为10~11 F到10~14 F。因此,要从大的杂散电容中提取出电极之间的微小电容信号,要求电容测量电路必须对杂散电容免疫[15];此外,还要求电路具有高的SNR以及较宽的带宽以实现高速数据采样率[16]。
本设计采用的交流C/V转换电路如图2所示,Cx为被测电容,C1、C2为寄生电容,C1的一端接地,C1一端的电流不会流入运算放大器,不会对Cx的测量带来影响;C2一端接地,另一端接在运放的反相端,处于虚地状态,故其两端电压为零,不会产生电流,它对输出Vo不会产生影响。运放反相输入端的流入电流为Vi流经Cx单独产生,所以此电路对寄生电容有一定的抑制作用。
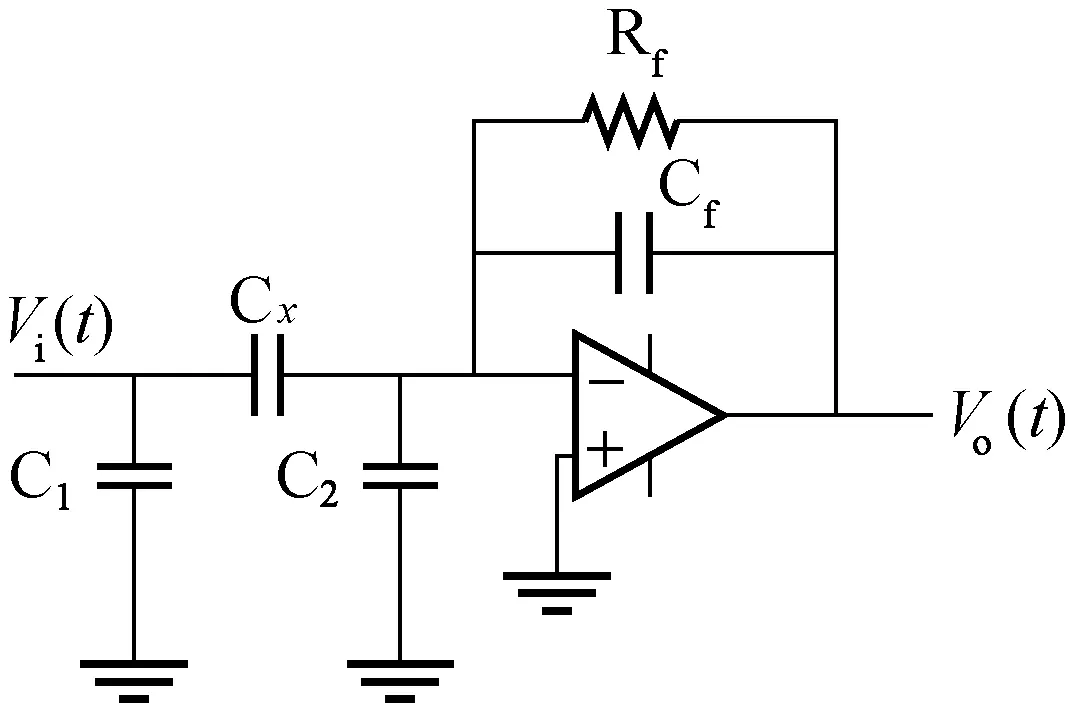
图2 C/V转换电路Fig.2 C/V converter circuit
将激励电压Vi施加到电路的输入端,电流流过电容被转换成电压。C/V转换器的输出电压与输入电压的关系式为:
(1)
式中:ω为输入信号的角频率;Cx为被测电容;Cf、Rf分别为反馈电容和反馈电阻。
目前采取的方法是取|jωCfRf|≫1,则:
(2)
输出电压值与测量的电容值成比例关系,采用正弦波激励信号作为载波存储被测信号的相位与幅值信息,输出的电压信号经采样后传送给处理器进行相敏解调,利用数字正交解调的方法从中提取幅值信息,经计算即可得到电容值。
本文提出采用三角波作为激励信号,利用微分电路的特性来测量电容信号。由于外界噪声的存在,微分电路运放对交流信号有放大作用;同时网络为高通滤波器,信号的相位滞后90°,系统不稳定,很容易进入自激震荡。在反馈端并联电容,使信号产生了90°的相移,能让系统保持稳定。
由于电路结构未变,微分电路的输入电压与输出电压的关系仍如式(1)所示。
若取|jωCfRf|≪1,则:
Vo(t)=-jωCxRfVi(t)
(3)
由式(3)可知,此时电路具有微分功能。
3 电路瞬态过程对比分析
正弦波作为激励信号时,电流流过反馈电容和反馈电阻,输入与输出的关系如式(1)所示。为研究电路的瞬态过程,将式(4)的信号作为激励信号:
(4)
输出的Laplace形式为:
(5)
则输出的时域响应为:
(6)
式中:α=arccot(ωCxRf);τ为C/V转换电路的时间常数,τ=CfRf;Vi为输入信号的幅值。
τ的取值决定电路输出的稳定时间,通常电路的稳定时间为5τ,因此,τ越小,系统响应越快[17]。在以正弦波为激励信号的设计中,取|jωCfRf|≫1,满足式(2),输出与输入信号的频率无关,与被测电容大小成正比。由于ECT系统实时性要求高,采用的激励信号频率一般为几百kHz,为满足|jωCfRf|≫1,此时时间常数τ的取值在10-3左右。这将影响电路的响应时间并限制系统的数据采集速率。
采用周期T、幅值为A的三角波作为激励信号,数学表达式为:
(7)
式中:Vi(t)为t时刻的输入电压值;n=0,1,2,3,…,且t>0;T为激励信号周期。用三角波作为激励信号,利用微分电路的特性对采集到的电容信号进行C/V转换处理。电路输入与输出关系如式(3)所示,则输出的时域响应为:
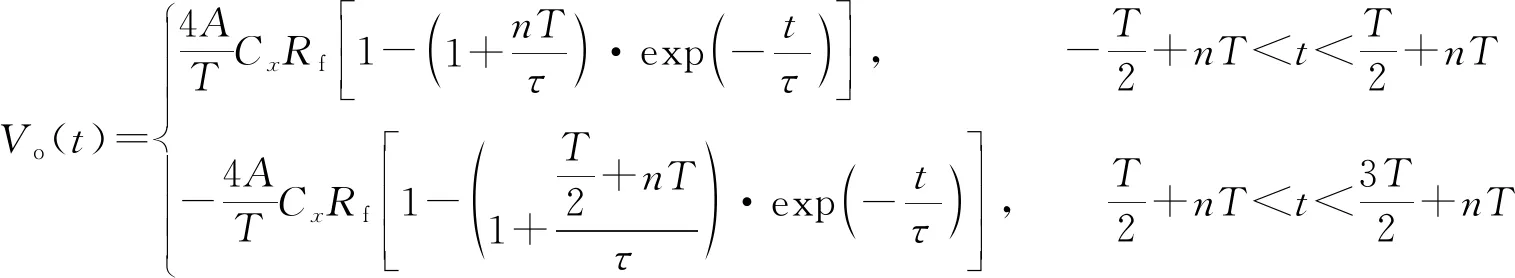
(8)
式中:n=0,1,2,3…,且t>0;τ=CfRf;T,A分别为激励信号的周期和幅值。在此设计中,为保留电路的微分特性,取|jωCfRf|≪1,由于激励频率为几百kHz,τ的值非常小,至少在10-7的数量级。此时的电路稳定时间会大于5τ,但由于τ的值非常小,与正弦波为激励信号的C/V转换电路相比,电路的稳定时间减少了几个数量级,能有效提高系统的实时性。由式(8)可知,被测电容值与输入信号频率并不会影响电路的稳定时间。图3为本设计电路在测量5 pF电容时的输出响应图,由图3可知电路的稳定时间缩短为0.65 μs。由式(8)可得电路的稳态输出为:
(9)
式中:n=0,1,2,3,…,且t>0。则稳态输出与输入的关系为:
V(o)p-p=4V(i)p-pfCxRf
(10)
式中f为激励信号频率。
由式(10)可知,输出的电压峰峰值与被测电容值、输入信号的频率和幅值成正比,输出电压信号为方波。

图3 电路瞬时响应曲线Fig.3 Circuit transient response curve
为了保证有较宽的测量范围,C/V转换电路必须有较高的灵敏度,灵敏度的定义为:
(11)
激励信号的频率为200 kHz,峰峰值为10 V,则由式(10)可得Rf=100 kΩ时的电路灵敏度的峰峰值达0.8 V/pF;同时,为了满足|jωCfRf|≪1,取反馈电容为1 pF。C/V转换输出需进行A/D转换处理,由于被测电容的动态范围一般在40 dB,为了充分利用ADC的量程测量信号的信噪比,可采用交流PGA(可编程增益)对C/V转换的输出进行不同倍数处理。课题组采用TI公司的可编程增益放大器THS7001作为C/V转换输出的后级放大,稳定时间为0.2 μs。
当采用正弦波激励信号时,如果满足|jωCfRf|≫1,则输出电压与输入电压呈比例关系。图4所示为被测电容值大小相同、激励信号幅值频率相同的情况下,激励源为正弦波与激励源为三角波经各自C/V转换后的输出波形。图中左侧y轴为正弦波标尺,单位为V;右侧y轴为方波标尺,单位为mV。由输出波形能快速计算出三角波测量电路的被测电容值;而利用正弦波作为激励源的C/V电路的输出仍为正弦波,不能直观地计算出被测电容值,需经过相敏解调的方法从输出中提取幅值信息。
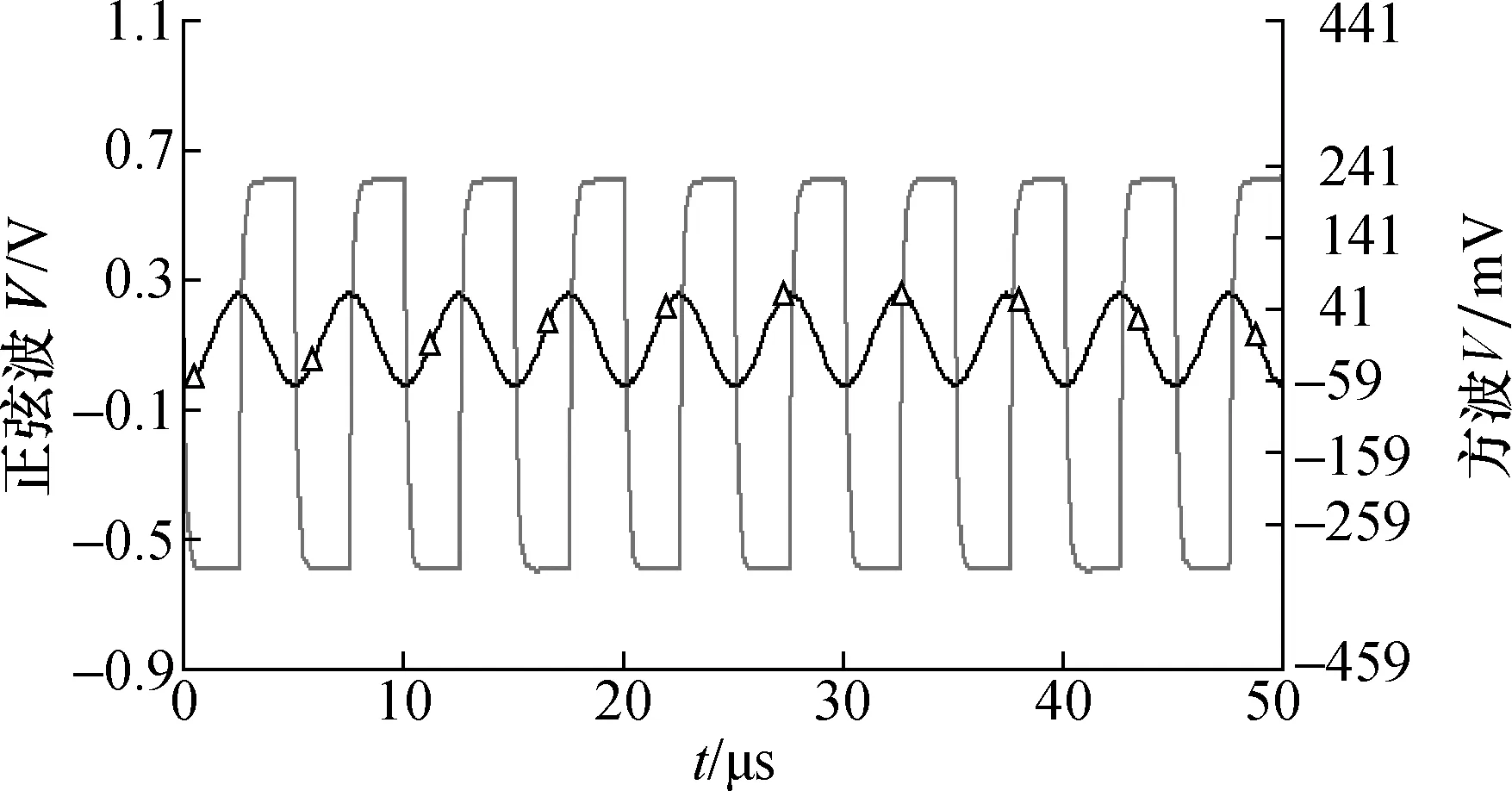
图4 正弦波激励与三角波激励输出波形Fig.4 Sine wave excitation and triangular wave excitation output waveforms
对参数选取后的电路进行仿真,图5所示为测量5 pF电容时在multisim中的仿真电路输出,由图可读出输出的峰峰值为3.998 V,与理论值相符。
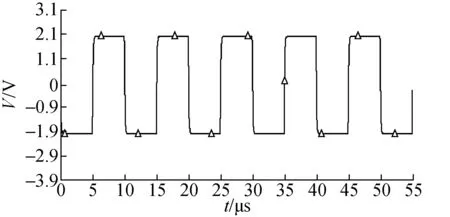
图5 测量电路仿真输出波形Fig.5 Measuring circuit simulation output waveform
由于ECT被测电容的范围为10-11~10-14F,从中选取部分电容值进行仿真,被测电容值与电路的输出关系见图6,拟合函数为V=0.799 8Cx-0.001 3。由于C/V转换电路的分辨率为0.8 V/pF,采用的AD芯片供电为±12 V,则C/V电路在测量大于30 pF的电容时进入饱和。电路最小可测量10 fF电容,因此电路的动态测量范围可达69 dB。本电路设计ECT测量各个环节所需时间见表1所示。对于12电极ECT成像系统成像速度计算式为:
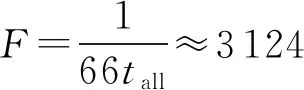
(12)
式中tall为数据在各个环节消耗总时间。

表1 ECT测量环节所需时间

图6 电容测量的电路输出Fig.6 Output of capacitance measuring circuit
4 电路性能测试
4.1 实验结果

图7 三角波激励信号Fig.7 Triangular wave excitation signal

图8 输出采样波形Fig.8 Output sampling waveform
实验之前利用Multisim仿真电路验证了方案的可行性,并与正弦波激励进行了比较。图7所示为三角波激励信号,峰峰值为10 V,频率200 kHz。由实验结果可知,由于输入信号与输出信号成微分关系,输入的三角波在波峰至波谷和波谷至波峰时斜率固定且相反,因此微分电路输出在两段时间内是定值且相反,为方波的形式。输出方波的频率与输入频率一致,采用10 MHz采样频率的AD芯片对输出信号进行采样,1个周期采样点的个数为50个。图8所示为示波器对方波采样的结果。在测量中,信噪比(SNR)用来比较所需要的电平信号与噪声电平的比例,定义为:
(13)

图9为选取的几个电容值进行测量并计算信号的信噪比所得的曲线。图中由每个电容测量150次计算所得。由图中数据可知:测量的电容值越小,信噪比越低。这是因为所测的电容值越小,电路的输出电压越低,而噪声的成分所占比重越大。
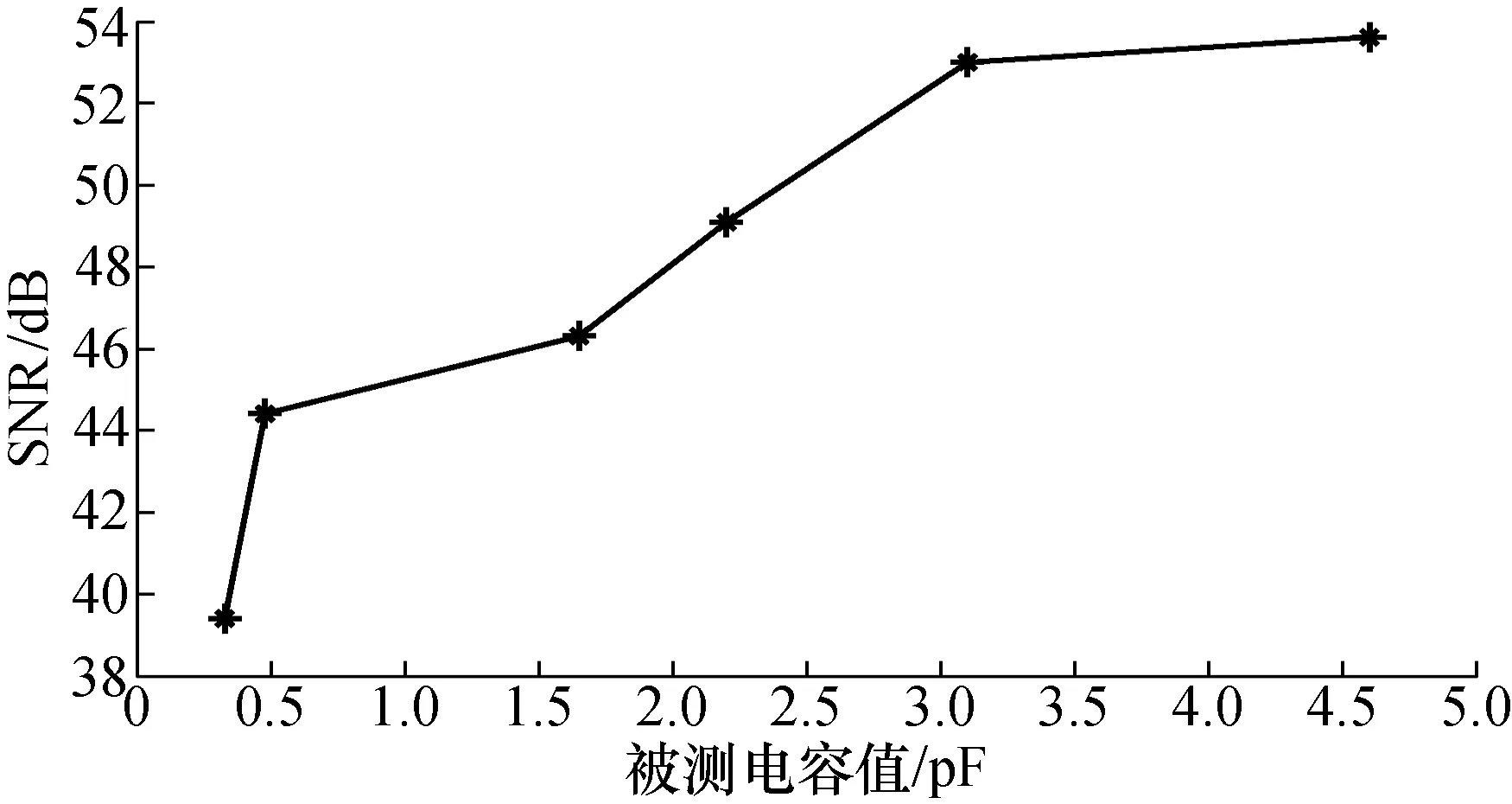
图9 测量值信噪比Fig.9 Measured SNR
由于方波是由基波和其它部分谐波累加而成,滤波器的截止频率不能太低,否则会导致方波失真。所以噪声无法完全滤除,仍然会有低频的噪声存在。由图8可以看出,电路有一定的稳定时间,这段时间采样的数据是不可用的。而由于噪声的存在,噪声的幅值与方波信号的幅值叠加,导致信号产生毛刺,而理想方波的幅值在每一个时刻均为相等的,所以对于采样到的数据得到的波形中,舍去幅值波动比较大采样点的数据,然后将剩下的采样点幅值做平均计算,能减小噪声的幅值对方波信号幅值的影响。本文采用中值滤波的方法对采样得到的数据进行处理。利用方波的峰峰值来计算被测电容的值,降低噪声对结果的影响,改善测量的精度。
表2为采用中值滤波前后信号信噪比的对比。由表2中数据可知,在滤波之前噪声所占的比例较大,严重影响信号的精度。在经过中值滤波对数据进行处理后,信号的信噪比得到大幅提升。

表2 信号滤波前后信噪比对比Tab.2 Signal-to-noise ratio of signal between without filtering and after filtering dB
4.2 电路重复性评价
本文采用示值重复性系统测量的方法来验证电路的稳定性。在测量条件恒定不变的条件下,短时间内对恒定电容值的电容进行重复测量,实验所得数据用Bessel公式计算标准差,按t分布给出扩展不确定度和相应的置信区间。Bessel公式为:
(14)
式中xi为重复测量所得的n个数据。
取4个市售2 pF电容(误差为(0.25 pF)串联,所得电容经LCR测量仪测量为0.485 pF,经微分电路重复测量100次的测量结果如图10所示。其示值重复性(置信区间为95.4%)为0.002 23。
5 结 论

图10 电路测量数据Fig.10 Circuit measurement data
实验分析表明,三角波激励的电容测量电路具有稳定性好、速度快、测量范围广的特性,符合ECT测量电路的要求;微分电路瞬态响应时间小,因此本方法的测量速度比正弦波激励的方法快。将其用于12电极ECT测量,可使测量速度提高到3 124帧/s。数据处理过程不需要相敏解调的特点也简化了软件设计,缩短了系统的开发周期。
