基于蚁群算法优化反向传播神经网络的港口吞吐量预测
2020-12-18李长安卢雪琴吴忠强张立杰
李长安, 卢雪琴, 吴忠强, 张立杰
(1.燕山大学先进锻压成形技术与科学教育部重点实验室,河北 秦皇岛 066004;2.燕山大学电气工程学院, 河北 秦皇岛 066004;3.燕山大学河北省重型机械流体动力传输与控制重点实验室, 河北 秦皇岛 066004;4.神华天津煤炭码头有限责任公司,天津 300457)
1 引 言
近年来, 物流行业发展迅速,港口在交通航运业中扮演的角色越来越重要。港口货物吞吐量是衡量港口生产经营规模的重要指标,关系到港口的具体规划设计和基础设施建设,科学合理地预测港口货物吞吐量不仅能更好地选择港口投资规模和运营策略,还有助于确定港口的发展方向和整体布局[1,2]。目前常用的港口货物吞吐量预测方法主要有:回归分析法、时间序列法、灰色系统法、人工智能方法以及组合模型法[3]。回归分析法是利用数理统计方法,对大量统计数据进行数学处理,通过建立因变量与自变量之间的函数表达式建立预测模型,方法简单,但是在解决非线性问题时具有一定的局限性。刘源等[4]利用回归分析法建立预测模型,对货运吞吐量进行了预测,预测结果接近实际值,达到了期望的预测效果。时间序列法是根据过去的时间序列数据预测事物的未来趋势,突出了时间因素在预测中的作用,但是忽略了外界因素的影响,当外界因素有较大变化时,预测结果会出现较大误差,不适用于长期预测。吴琛等[5]利用时间序列模型对港口集装箱吞吐量进行预测,并验证了预测模型的有效性和精确性。灰色系统法是通过影响因素之间的关联分析,对统计数据进行处理,生成有规律的数据序列,然后建立模型并预测,计算量小,简单可靠,但是对模型的依赖性较强,不同模型需要不同的关联度计算方法,且只适用于中短期的具有指数增长型模型的预测。余国刚等[6]运用灰色预测模型对集装箱吞吐量进行了预测,得到的预测结果误差小,精度高。人工智能方法主要包括粗糙集方法、遗传算法、人工神经网络和支持向量机等[7,8]。人工智能方法对数据的概率分布等额外信息没有严格的要求,有更好的包容性和适应能力,但也有其自身的缺陷,如易受网络本身拓扑结构复杂性和数据复杂性的影响,泛化能力较差。朱庆辉等[9]利用小波神经网络建模对港口集装箱吞吐量进行预测,预测精度高;刘美莲等[10]利用灰色系统法对港口货物吞吐量相关影响因素进行筛选分析,并结合反向传播(BP, back propagation)神经网络建立预测模型,预测结果精确。组合模型法是将已建立的各个单项模型以一定方式组合后对吞吐量进行预测,提高了模型的性能,但是结构往往比较复杂,计算量大、速度慢。文献[11]构建了一种结合投影寻踪回归(projection pursuit regression)和遗传规划(genetic programming)算法的组合预测模型对港口吞吐量进行预测,预测效果优于单个模型的预测效果;文献[12]提出了一种新的MARS-RSVR(multivariable adaptive regression splines-robust support vector regression)组合方法进行预测,提高了预测精度。
影响港口货物吞吐量的因素很多,而且各个因素之间存在复杂的非线性关系。BP神经网络可以以任意精度逼近非线性函数[13],而且原理简单,通用性强,是较理想的建模工具。然而,BP神经网络在训练过程中学习速度较慢,并且容易陷入局部极值,为了解决这些问题,提出一种蚁群算法(ant colony algorithm)优化BP神经网络(AC-BP)的港口吞吐量预测方法,蚁群算法具有全局搜索能力,分布式计算和鲁棒性强等特点,利用蚁群算法优化BP神经网络建立预测模型,有利于加快BP神经网络的收敛速度,避免易陷入局部极值的问题,进一步提高建模精度。对港口货物吞吐量的预测结果表明,与传统BP神经网络相比,蚁群算法优化的BP神经网络性能更强,收敛速度更快,预测精度更高。
2 蚁群算法优化BP神经网络
2.1 BP神经网络
BP神经网络是一种前馈型神经网络,由输入层,隐含层和输出层组成,其结构图如图1所示。
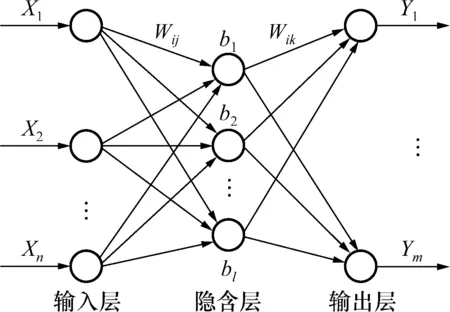
图1 BP神经网络结构图Fig.1 Structure diagram of BP neural network
图1中,X1,X2,…,Xn是网络的输入;Y1,Y2,…,Ym是网络的输出;Wij和Wjk为网络的权值;b1,b2,…,bl为网络的阈值;l为隐含层神经元个数。整个神经网络模型可以看成一个非线性函数,网络的输入X1,X2,…,Xn为自变量,网络的输出Y1,Y2,…,Ym为因变量,自变量和因变量之间构成了函数映射关系。
BP神经网络的主要特点是信号前向传播,误差反向传播。设定期望输出值,网络根据预测输出与期望输出的误差对比结果进行反向传播,调整各神经元的权值和阈值。整个过程反复进行,直到网络样本输出误差E<ε(ε为期望误差精度)或训练达到最大迭代次数Nc为止。
网络样本输出误差E为:
(1)
式中:L为网络样本数;O(l)和Y(l)分别为第l个网络样本的实际输出值和期望输出值。
在BP神经网络学习过程中,网络初始权值对学习效果和收敛速度有重要影响,理想的初始值可以使网络模型较快收敛到最优解,若初始权值和阈值选取不当,会导致网络的收敛速度慢并且容易陷入局部极小值[14]。本文采用蚁群算法优化BP神经网络建立预测模型,利用蚁群算法优化BP神经网络的初始权值、阈值,使网络输出快速逼近期望输出,以加快BP神经网络的收敛速度,解决易陷入局部极值的问题,能达到更好的预测效果。
2.2 蚁群算法
蚁群算法是通过模拟自然界蚂蚁的寻径方式得到的一种启发式随机搜索算法[15]。基本蚁群算法表述如下[16]:在初始时刻,将m只蚂蚁随机地放到n座城市上,此时各路径上的信息素均相等,即设τij(0)=c(c为一常数),接下来,蚂蚁k(1≤k≤m)根据路径上的信息素量和启发式信息(两城市间距离)来选择下一座城市,并通过禁忌表(tabu)来记录当前所走过的城市。
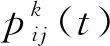
(2)
式中:Jk(i)={1,2,…,n}-lt,k为蚂蚁下一步的备选城市。禁忌表lt,k记录了蚂蚁k当前所走过的城市,当所有城市都加入禁忌表lt,k,蚂蚁k便完成了一次周游。ηij为一个启发式因子,表示蚂蚁k从城市i转移到城市j的期望程度,通常取2个城市之间距离的倒数。α为信息启发式因子;β为期望启发式因子。
在t+n时刻,当所有蚂蚁结束一次循环后,利用式(3)对各路径上的信息素进行更新调整。
τij(t+n)=(1-ρ)·τij(t)+Δτij
(3)
式中:ρ为路径上信息素的挥发程度,取值为[0,1],1-ρ为信息素的残留程度;Δτij为在本次循环结束后m只蚂蚁留在路径上的总信息量的增量为:
(4)

(5)
式中:Q为正常数,Lk为蚂蚁k在本次循环中所走过路径的长度。
当所有蚂蚁都收敛到相同路径或循环次数达到最大迭代次数时,算法终止。
2.3 AC-BP算法
蚁群算法优化BP神经网络的基本思想是:假设有m只蚂蚁,每只蚂蚁按照状态转移概率公式选择行径路径并记录具体的参数值,将这些参数值作为BP神经网络的初始权值、阈值,计算训练样本的输出误差,再利用输出误差和期望误差的对比结果来调整蚂蚁行经路径上的信息素值和路径选择。这样不断地重复优化,直到所有蚂蚁收敛到相同路径时,迭代次数完成,得到最优初始解。将得到的最优初始解作为BP神经网络的初始权值和阈值进一步训练网络,直到误差精度达到期望值。
设BP神经网络有M个权值和阈值,每个权值或阈值有n个数值可供选择,这n个数值在[0,1]区间内随机生成,组成集合IPi(1≤i≤M)。令式(2)中的ηij=α=β=1,得到简化的状态转移概率:
(6)
式中:τj(IPi)为集合IPi中元素j的信息素值。
在初始时刻,同时释放m只蚂蚁,蚂蚁k(1≤k≤m)从集合IPi出发,根据式(6)的状态转移概率在集合IPi中选择元素j。每只蚂蚁从各个集合中挑选一个元素且仅挑选一次。
由式(3)得到对集合IPi(1≤i≤M)中的每个元素进行信息素更新的公式:
τj(IPi)(t+M)=(1-ρ)·τj(IPi)(t)+Δτj(IPi)
(7)
式中:Δτj(IPi)为本次循环中,集合IPi中元素j的信息素的增量,据式(4)可知:
(8)
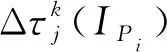
(9)
式中ek为第k只蚂蚁选择的初始权值和阈值训练BP神经网络得到的实际输出与期望输出之间的误差。
2.4 算法的实现
蚁群算法优化BP神经网络初始权值、阈值的具体步骤如下:
1) 参数初始化。设置集合IPi中元素j的初始信息素值τj(IPi)(0),蚂蚁数量m,信息素挥发系数ρ,信息素增量强度系数Q,最大迭代次数G。
2) 蚂蚁选择参数。m只蚂蚁按照状态转移概率公式(6)从各个集合中挑选元素,每只蚂蚁挑选的所有元素的组合构成了神经网络的一组初始权值、阈值。
3) 当m只蚂蚁都完成一次循环后,利用步骤2)中选取的m组初始权值、阈值训练神经网络,并用误差函数式(1)计算网络的输出误差,记录误差最小的一组权值、阈值,比较此时的最小误差与期望误差ε的大小,若小于期望误差ε,则转到步骤6),否则转到步骤4)。
4) 根据式(7)对集合IPi(1≤i≤M)中的每个元素进行信息素更新。
5) 重复上述步骤2)、3),直到所有蚂蚁收敛到了相同路径,达到了最大迭代次数G。
6) 将蚁群算法选出的一组最优初始解作为神经网络的初始权值、阈值,利用BP算法进一步训练神经网络,直到满足退出条件。
3 港口货物吞吐量预测
3.1 数据的选择与处理
选取某港口2000~2009年的货物吞吐量数据作为训练样本,选取2010~2014年的货物吞吐量数据作为测试样本,具体数据如表1所示。
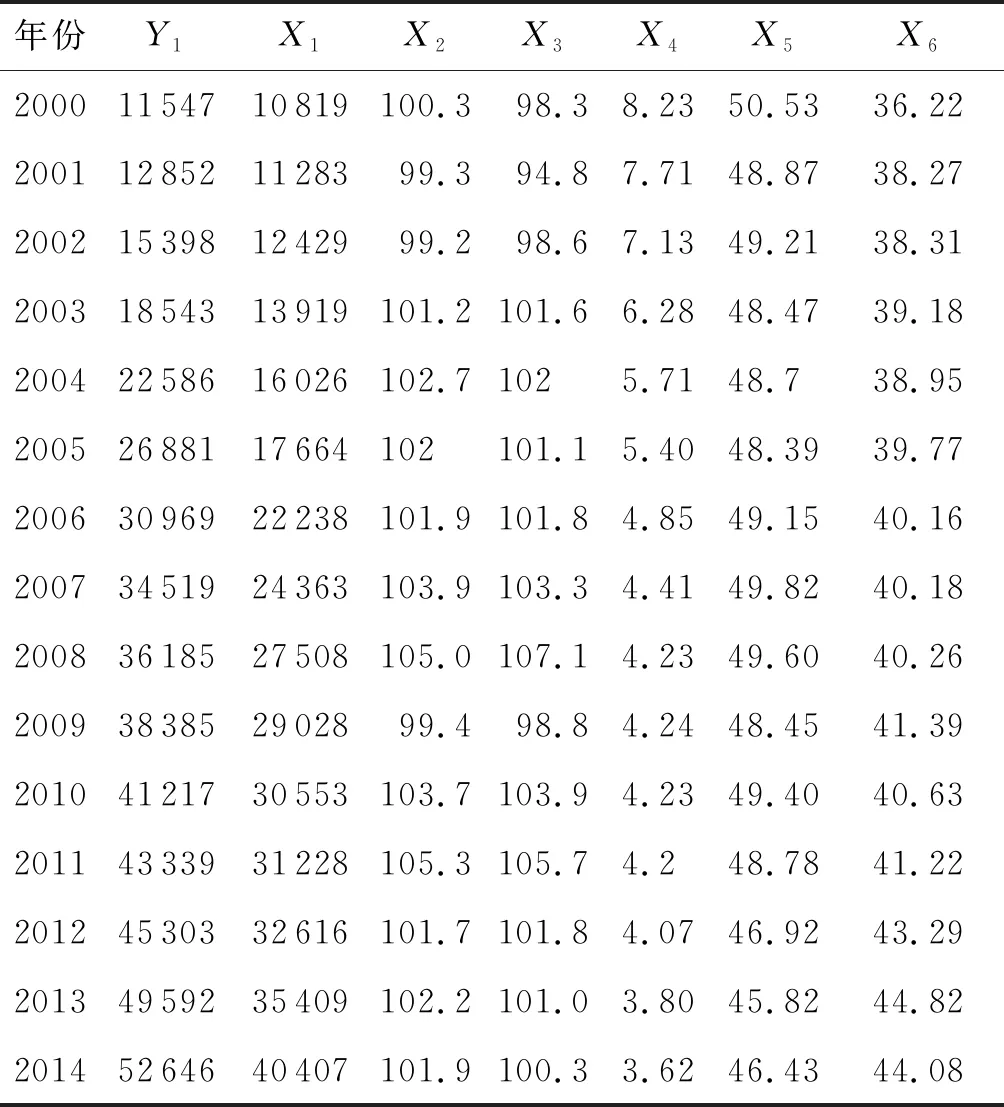
表1 2000~2014某港口货物吞吐量及影响因素统计表Tab.1 Statistics table of cargo throughput and its influencing factors in a port 2000~2004 104t
表1中输入样本为影响港口货物吞吐量的各种因素,主要包括集疏运货运量X1(104t)、居民消费价格总指数X2、商品零售价格总指数X3、港口固定资产投资总额X4(亿元)、水路货运量X5(104t)和铁路货运量X6(104t),共6个输入变量[17,18],输出样本为港口货物吞吐量Y1(104t)。由于港口货物吞吐量各影响因素的数值大小差异很大,容易影响BP神经网络的学习速度,干扰预测结果,所以需要用式(10)对样本数据进行归一化处理。
(10)
式中:Xi为待归一化样本数据;Xmax为样本数据的最大值;Xmin为样本数据的最小值;X′i为样本数据归一化处理后的值。
3.2 网络参数设置
参数设置:设蚂蚁数量m=25,信息素挥发系数ρ=0.3,信息素增量强度系数Q=1,最大迭代次数G=500。采用3层结构的BP神经网络对样本数据进行学习训练,输入层节点数为6,输出层节点数为1,根据试凑法确定隐含层神经元个数。经过反复学习与训练,当隐含层神经元个数为6时,网络的预测误差较小,训练结果相对稳定。设置最大训练次数为5 000,学习误差为1×10-5,学习率为0.01。
3.3 预测结果及分析
利用2000~2009年的数据,分别对BP、RBF、模糊神经网络和AC-BP这4种模型进行训练,利用训练好的模型对2010~2014年的港口货物吞吐量进行预测。设定2种模型的神经网络结构和主要参数均相同,分别得到训练结果及训练误差如图2~图5所示。

图2 BP训练结果Fig.2 BP training results
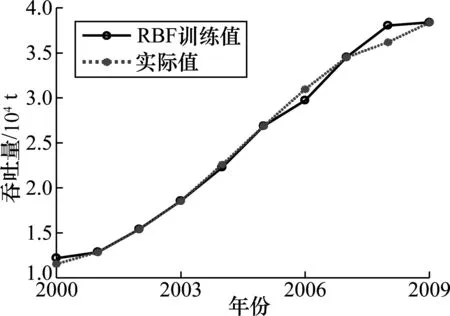
图3 RBF训练结果Fig.3 RBF training results

图4 模糊神经网络训练结果Fig.4 Training results of fuzzy neural network

图5 AC-BP训练结果Fig.5 AC-BP training results
由图2~图5的拟合结果可看出,AC-BP模型的训练结果最好,模型输出最接近期望值,具有最好的性能。模糊神经网络的拟合结果优于RBF网络的拟合结果;RBF网络的拟合结果优于BP网络的拟合结果。BP网络的拟合结果最差。
测试样本的预测结果如图6~图9所示。

图6 BP预测结果Fig.6 BP forecast results

图7 RBF预测结果Fig.7 RBF forecast results

图8 模糊神经网络预测结果Fig.8 Forecast results of fuzzy neural network

图9 AC-BP预测结果Fig.9 AC-BP forecast results
由图6~图9对比可看出,AC-BP预测模型的预测结果曲线更为平滑,与实际值曲线更贴近,预测效果更好。为了进一步证明所提AC-BP预测模型的准确性,分别计算4种预测模型的平均绝对百分比误差MAPE作为模型有效性的评价指标。MAPE的定义为:
(11)
式中N为测试集样本个数。
由式(11)得到BP预测模型的MAPE为6.566%,RBF预测模型的MAPE为4.990%,模糊神经网络预测模型的MAPE为3.734%,AC-BP预测模型的MAPE为2.826%,AC-BP预测模型明显优于其它3个预测模型,预测精度最高。
4 结 论
利用蚁群算法具有较强的鲁棒性、全局搜索能力和分布式计算等特点,对BP神经网络的初始权值、阈值进行了优化,并运用优化后的BP神经网络对港口货物吞吐量进行了预测。预测结果表明:蚁群算法优化BP神经网络的预测模型预测精度高、训练速度快、效果理想,具有较大的应用价值。
