三维剂量测量系统中传统深度估计算法与快速EPI算法对纵向分辨率影响的对比

乔 霈，闫学文，李德源，牛蒙青

(中国辐射防护研究院，山西 太原 030006)

目前，放射治疗广泛应用于癌症等人体疾病治疗中，在放射治疗过程中，剂量的估算至关重要，准确的剂量估算可以避免患者出现超剂量照射风险[1]。光场成像技术作为现代图像测量的一个分支，广泛应用于工业制造、机器视觉等领域。使用光场成像技术，通过获取光场的二维图像，利用深度估计算法进行反演，进而获取光场三维分布信息。场景的三维信息包括高度、宽度和深度。深度信息能更好的展示物体在三维空间中的结构，获取物体深度信息，可以广泛应用于计算机视觉、成像、医疗影像等方面。基于光场图像的深度信息提取方法主要通过计算视差来实现。通过获取空间中同一物体在不同视点下的两幅或者多幅视差信息，利用光学传播的几何原理，计算出物体的深度信息。

目前，深度估计方法主要分为两大类：主动深度估计方法和被动深度估计方法[2]。主动深度估计方法是根据场景信息，控制摄像机系统和成像环境，然后，获得场景信息。该方法获取深度信息的准确度较高，但是其测量系统体积较大，成本较高，一般不被大家广泛使用。被动深度估计方法，与主动方法差异较大，通过调整摄像机镜头的光圈，找到拍摄图片时各个像素点最佳的拍摄角度，然后，根据相机的成像原理，计算各像素的清晰度，用清晰的像素点构成一张全聚焦图像，对这张图进行深度估计，最后进行优化处理，得到图像的场景深度信息。这种方法虽然操作较复杂，但是得到的深度信息准确。光场相机通过在主镜头组和图像传感器(CCD芯片或CMOS芯片)之间的特定位置加入微透镜阵列[3]，实现采集物体光强和记录光线方向的信息[4]，因此，它不仅可以捕获图像的平面信息，还可以通过深度估计方法得到图像的深度信息。本项目组利用光场相机和组织等效的闪烁材料构建三维剂量测量系统，利用光场相机获取质子或重离子在组织等效闪烁材料中产生闪烁体光的三维分布信息来计算质子或重离子在组织等效材料中三维剂量分布。为了获取图像的三维信息，需要用深度估计算法得到图像的深度信息，现有的被动深度估计算法主要有传统的深度估计算法[5]和快速极线平面图(epipolar plane image, EPI)的深度估计算法[6]。三维场景中物体在不同深度位置处获得图像的像素存在差异，为了在不同的深度得到图像的最佳像素，引入图像的纵向分辨率，即图像在不同深度位置处的像素与尺寸的比例。并且，深度估计算法对图像纵向分辨率的影响至关重要，而图像的纵向分辨率又直接影响三维剂量的测量准确性，因此，开展深度估计算法对图像纵向分辨率影响的对比研究尤为重要。

尽管深度估计算法已取得显著进展，但是在三维剂量测量中，深度估计算法对图像纵向分辨率的影响未有深入研究。因此，本文围绕两种深度估计算法对图像的纵向分辨率影响进行对比研究，结合其在三维剂量测量领域实际情况展开分析。

1 深度估计方法

利用光场相机获取实体的初始图片，然后，采用传统的深度估计算法和快速极线平面图(epipolar plane image, EPI)算法得到图像的深度信息，通过实验结果的对比及分析，比较两种方法对图像纵向分辨率的影响。

1.1 传统深度估计算法

光场相机由镜头、微透镜阵列和图像传感器组成。在图像获取中，为了得到清晰度高的图像，采用聚焦型光场相机获取图像，成像原理如图1所示，物体所有方向上的光线通过主透镜汇聚到微透镜上，每个微透镜将得到主透镜像面上的一个区域内的图像。由于方向不同，继而散射到微透镜后面的传感器像元上，使得主透镜像面上的景物二次成像。a、b分别为微透镜到主透镜像平面的距离、微透镜到传感器的距离，因此，光场相机对光场的方向分辨率为a/b，a、b满足透镜的基本成像公式，公式见(1)，通过调整参数a、b来实现光场的方向采样。

图1 聚焦型光场相机的成像原理图Fig.1 Imaging schematic of a focused plenoptic camera

(1)

式中，f为微透镜的焦距，根据具体的微透镜获得，a为微透镜到主透镜像平面的距离，b为微透镜到传感器的距离。

聚焦型光场相机拍摄所得的图像示于图2，被拍摄物体会在多个微透镜图像中出现，每个微透镜图像都与相邻的图像有重叠区域。由于微透镜是圆形，为了方便后续的图像处理，本文选择微透镜图像中的一部分做处理，示于图3，选取圆形图像中长度为m的矩形区域，进行整图拼接得到重组后的图像，重组后的图像示于图4。

图2 聚焦型光场相机拍摄图Fig.2 Photograph of a focused plenoptic camera

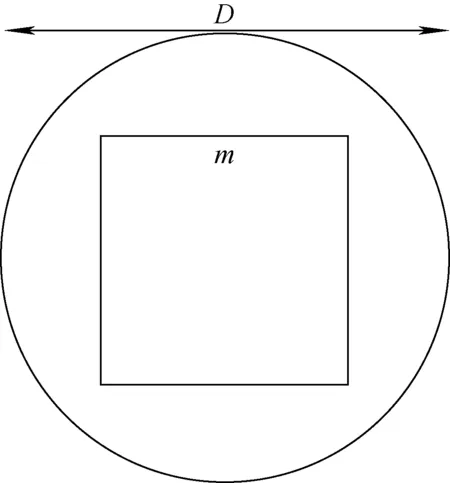
图3 图像块的裁剪模型Fig.3 Cropping model of the image block

图4 重组后的图像Fig.4 The reorganized image

图4中，微透镜的个数为Nxx×Ny，各个微透镜图像的大小为nxx×ny，图像块的大小为m×m。

依据重组的图像获取图片的深度估计信息。详细的原理示于图5。首先，将微透镜图像中m′×m′的图像块A表示为Am；然后，在与A相邻的微透镜子图像B中平行的选取多个图像块Bm；计算Am与若干Bm的相关值，并记录获得最大相关值的图像块Bm的中心位置kx。以此类推，对微透镜图像A和C进行上述操作，得到ky。最后，将水平方向的kx和竖直方向的ky求平均值k，k即为微透镜子图像A的相对深度。遍历图像中的每一个微透镜子图像，得到由k构成的矩阵即为三维图像的深度信息K。

图5 深度估计算法原理图Fig.5 Schematic of depth estimation algorithm

1.2 快速EPI深度估计算法

在光场成像的图像处理过程中，由于序列图像中的各个图像单独处理操作比较繁琐，因此引入了EPI[7]结构，将序列图像看成一个整体进行切分[8]，使得操作的复杂度降低。

图6 极平面、极线示意图Fig.6 Schematic diagram of polar plane and polar line

为了更好的理解EPI，首先需要清楚极平面、极线等的形成原理。假设两个相机对场景中的点M成像，示意图示于图6。场景中的任意点M，均可以和两个透镜的中心连线形成平面，该平面为极平面。然后，极平面与两个像面各自相交，所对应的交线即为极线。极平面上的所有点在像面1上的投影都在像面1与极平面相交的极线上，同理，像面2上的投影也在对应的极线上。因此，可以得出，所有极平面上的点在各自像面上的投影都在相应的极线上。在搜索图像的匹配点时，可以依据其对应的极线对，使二维平面的搜索降到一维极线的搜索，大大降低了匹配点的搜索范围。因此，寻找点M在两个像平面中的匹配点，只需要在极线中搜索即可。

图像在极平面上的点都可以投影到对应的极线上，因此，图像极平面中的信息可以包含在对应的极线序列中。在分析图像序列时，为了能够将信息集中处理，需要将这些极线序列对按照某种特定的顺序进行排列，形成一幅新的图像，这个新的图像即为EPI，它涵盖了图像极平面中所有的特征信息。

图7 水平方向EPI序列表示Fig.7 Horizontal EPI sequence representation

EPI场景可以通过多个摄像机从不同的视角同时拍摄同一个场景，或者一个相机从不同的位置捕捉场景[9]，这样构成的多个视图图像形成了EPI图像；本研究中，在快速EPI深度全光相机获取深度分辨率[6]中，首先将原始的光场图像用EPI表示。EPI块由水平方向EPI表示和竖直方向EPI表示两块构成，水平和竖直方向各自EPI表示的获取方式如图7和图8所示，每一个正方形代表一个图像块的像素矩阵分布，图7依次从图像块A相邻的几个微透镜构成的像素块矩阵中各抽取中间一行的像素，按照图中Block1、Block2、Block3的排列方式构成三行像素组矩阵，即为水平方向EPI。同理，可以得到图8中竖直方向的EPI。将水平和垂直的EPI表示进行连接构成最终的EPI表示，示于图9。

图8 垂直方向EPI表示Fig.8 Vertical EPI sequence representation

由图7可知，对于微透镜阵列中的子图像块A，选择其相邻的各图像块中间一行像素点，按照图中的顺序进行排列和拼接，构成新的水平EPI表示。图8选取与子图像块A相邻的各图像块中间一列像素点，构成新的垂直EPI表示。

接下来，需要利用图像的EPI序列表示获取图像的深度估计信息。首先，引入一个差异值d，利用d值来移动EPI序列中像素点的位置。EPI序列表示的第一行像素点不做改变，第二行像素点平移d，第三行像素点平移2d，以此类推(本文中只对三行做位移)。因此，得到一个平移后的EPI序列。然后，计算每一列重合像素的方差之和，具体计算如公式(2)所示，改变d值的大小，寻找方差值最小时对应的d值为d′，如公式(3)所示，此时，d′为微透镜子图像A的深度估计值；最后，遍历每一个微透镜子图像，得到各个子图像的d′值形成的深度信息矩阵D。

(2)

(3)

公式(2)中j为EPI序列中像素点所在的列。

图9 最终的EPI序列表示Fig.9 Final EPI sequence representation

2 两种深度估计算法对纵向分辨率的影响

本文使用java语言实现上述第1节中的两种深度估计算法，两种算法的结果均由一个矩阵展示。传统的深度估计算法获取深度信息时得到的矩阵为K，该方法是从相邻图像块间的相关度方面进行考虑；快速EPI全光相机获取深度信息的方法得到的矩阵为D，该方法从方差的角度分析并获取每一列像素点的方差，然后选取方差最小值对应的d，其含义是从相邻的图像块中寻找差异最小(即偏离程度最小)值。通过比较两种算法分别得到的矩阵K和D，来衡量方法对图像纵向分辨率的影响程度。

本文以光场相机捕获的图像图2为研究示例，通过图像的初步处理得到图2所示重组后的图像，在图3的基础上，分别用传统的深度估计算法获取深度信息和快速EPI获取深度信息算法得到各自对应的深度信息矩阵K和D。两种方法的实验结果列于表1。将传统的深度估计算法简称为算法1，快速EPI获取深度信息的方法简称为算法2。

表1 算法1和算法2获取的深度信息矩阵结果Table 1 Depth information matrix results obtained by Algorithm 1 and Algorithm 2

由表1的图像深度信息计算结果可知，算法1由于是相关度结果，因此范围在0～1之间，整体的相关度结果比较离散，表示与各个图像块最相关的相关系数值；算法2得到的为差异值d′的分布结果，但是，从结果D可以看出深度信息均集中在d′为74的邻近值。

两种深度信息获取算法都是通过获取图像的深度值，衡量图像的三维信息。图像的深度范围一般比较广，这样才能充分体现图像的纵向分辨率，并且为后期全聚焦图像确定良好和健壮的深度估计[7]。结果值波动越小，说明该图像的深度值相差不大，不能很好的体现图像的纵向分辨率。

从算法的原理角度进行分析，我们发现算法2在深度信息获取过程中，首先对图像的EPI序列表示进行位移变化，然后再计算每个重叠列的方差和，选择最小方差对应的d值。每次循环d的过程中，由于EPI序列长度较短，并且序列中的像素值较大，因此方差和的变化很微小，导致最终d值相差较小，而且在d临近末端时，由于像素值变少，使得方差更容易最小。因此，从原理的角度考虑，算法1在图像范围较小的情况下也能获得高的纵向分辨率，然而，算法2需要在图像分布范围较广的情况下才能发挥其算法的优势。

从算法获得的结果进行分析，表1中两种算法的结果可以得知，算法1获得子图像块的相关度值反映深度信息，矩阵K中各个相关度值k比较离散，可以较充分的反映图像的深度信息，因而对图像的纵向分辨率影响更大；然而，算法2得到的d′值差异较小，这样很难展现出图像的深度信息。

在三维剂量测量系统中，质子或重离子在组织等效闪烁材料中沉积能量产生闪烁光，且产生的闪烁光的量与质子或重离子所沉积的能量成正比。且能量以布拉格峰的形式沉积，产生的光分布的横向分布较窄。在此种情况下，传统的深度估计算法获得图像的纵向分辨率更好，因此，传统的深度估计算法更适用于质子或重离子放射治疗过程中的三维剂量测量。

3 结论

光场相机突破了传统相机记录三维场景的不完备性[10]，相较于其他成像装置而言，采集方式便捷，获取的光场数据精确，这使得本文的图像采集工作顺利开展。在三维剂量测量系统中，通过光场相机获得闪烁光的平面分布图像，然后利用两种深度信息获取算法挖掘图像中的三维信息，分析和比较两种深度估计算法对图像纵向分辨率的影响，由于质子或重离子在组织等效的闪烁材料中以布拉格峰形式进行能量沉积，使得光的横向分布较窄，传统的深度估计算法能够针对该问题得到较高的图像纵向分辨率。而快速EPI深度估计算法逻辑结构更简单，更适合于图像分布范围较大的应用场合。