关于核电主泵轴系临界转速计算及稳定性标准的探讨

杨德马

(东方法马通核泵有限公司，四川 德阳 618000)

核主泵是反应堆冷却剂系统的主要设备之一，其主要作用是驱动反应堆内部冷却剂的循环，在堆芯一回路系统冲水时排气；在升温升压过程中进行循环升温；在正常运行时将堆芯产生的热量通过冷却剂将热量传递到蒸汽发生器进而加热二回路给水成蒸汽，驱动汽轮机进行发电；如果主泵不能长期安全稳定运行，核反应堆的热量将不能及时导出而出现超压或者熔堆事故。因此主泵是压水反应堆核电站的心脏，是压水反应堆的主要设备；主泵的稳定性对核电站的安全有着至关重要的作用。

对于立式、单级离心的核轴封泵，属于高速旋转机械，其主泵的支撑系统通常在电机端采用可倾式油润滑轴承，水泵端采用水润滑的圆柱轴承；在考虑主泵油膜刚度及弹性支撑系统后，主泵通常需要跨越多阶临界转速启动运行，因此轴系临界转速安全性判定标准在主泵设计之初对主泵稳定性的评估至关重要。

本文将以国内某主泵为列，对主泵转子系统的简化、临界转速的计算及临界转速判定标准进行探讨

1 理论临界转速分析方法

理论临界转速的是基于传统的转子动力学方程，以研究转子振动为出发点，其运动方程可写为：

(1)

式中：[M]——质量矩阵;

[Jp]——系统回转矩阵;

[C]——系统阻尼矩阵;

[K]——系统刚度矩阵;

{f(t)}——外部激励载荷;

Ω——转子旋转速度。

求解转子动力学方程的特征值，可以得到：

det{ω2[M]+ω([C]+Ω[Jp])+[K]}=0

(2)

式中：ω——转子涡动频率。

当转子的旋转速度Ω等于转子涡动频率ω时，Ω称为临界转速。

对于整个转子-轴承系统的刚度[K]以及阻尼[C]，其通常包含两个部分：

(1)转子结构本身的刚度及阻尼;

(2)转子支撑系统的刚度及阻尼:

1)基础刚度及阻尼;

2)轴承油膜刚度及阻尼。

在本文对主泵的分析中，考虑主泵在启动及稳定运行时，转速对轴承油膜刚度及阻尼系数的影响，将转子—轴承—基础系统作整体动力分析。

2 轴系横振仿真模型的建立

对于轴系仿真模型的建立，主要采用有限元法，将转子划分为轴段、集中质量、转动惯量和轴承支撑单元，利用拉格朗日方程或者哈密尔顿方程建立每个单元的运动方程，从而得到各单元的刚度矩阵、质量矩阵、阻尼矩阵、陀螺效应矩阵等。根据各微元段的平衡方程及各节点之间力的平衡条件，求解方程组得到转子的动力特性。

对于主泵规则轴段，直接采用以铁木辛柯梁理论为基础的圆柱单元进行模拟；对于复杂形状的部件比如转子支架、叶轮等，则通过有限元计算等效参数后再用圆柱单元进行模拟；轴系实体及仿真模型，请见图1。

图1 主泵轴系实体模型及仿真模型Fig.1 The shaft line solid model and simulationmodel for reactor coolant pump

2.1 飞轮简化

飞轮是主泵的储能装置，在核电厂发生断电事故时，飞轮将释放能量驱动泵轴继续运转，为反应堆提供冷却剂，避免堆芯损坏。飞轮在简化时，主要考虑其质量及转动惯量的影响，不考虑飞轮本身的刚度。

2.2 电机转子简化

由于电机转子支架是非规则的结构，我们采用分段线性的方法对其进行简化，并根据截面面积及截面惯性矩求解简化等效参数：

(3)

求解上述方程组得到：

(4)

对于电机转子其他部件，诸如转子导条、铁芯等均只考虑其质量及转动惯量。

2.3 叶轮简化

本文在建立主泵轴系仿真模型时，考虑了叶轮刚度对于轴系稳定性的影响，通过建立叶轮的有限元模型，求解叶轮的等效截面积及等效弯曲惯性矩，进而通过公式 (1)得到轴系建模参数。

等效截面积及等效弯曲惯性矩的通过有限元进行求解，叶轮有限元模型，见图2。

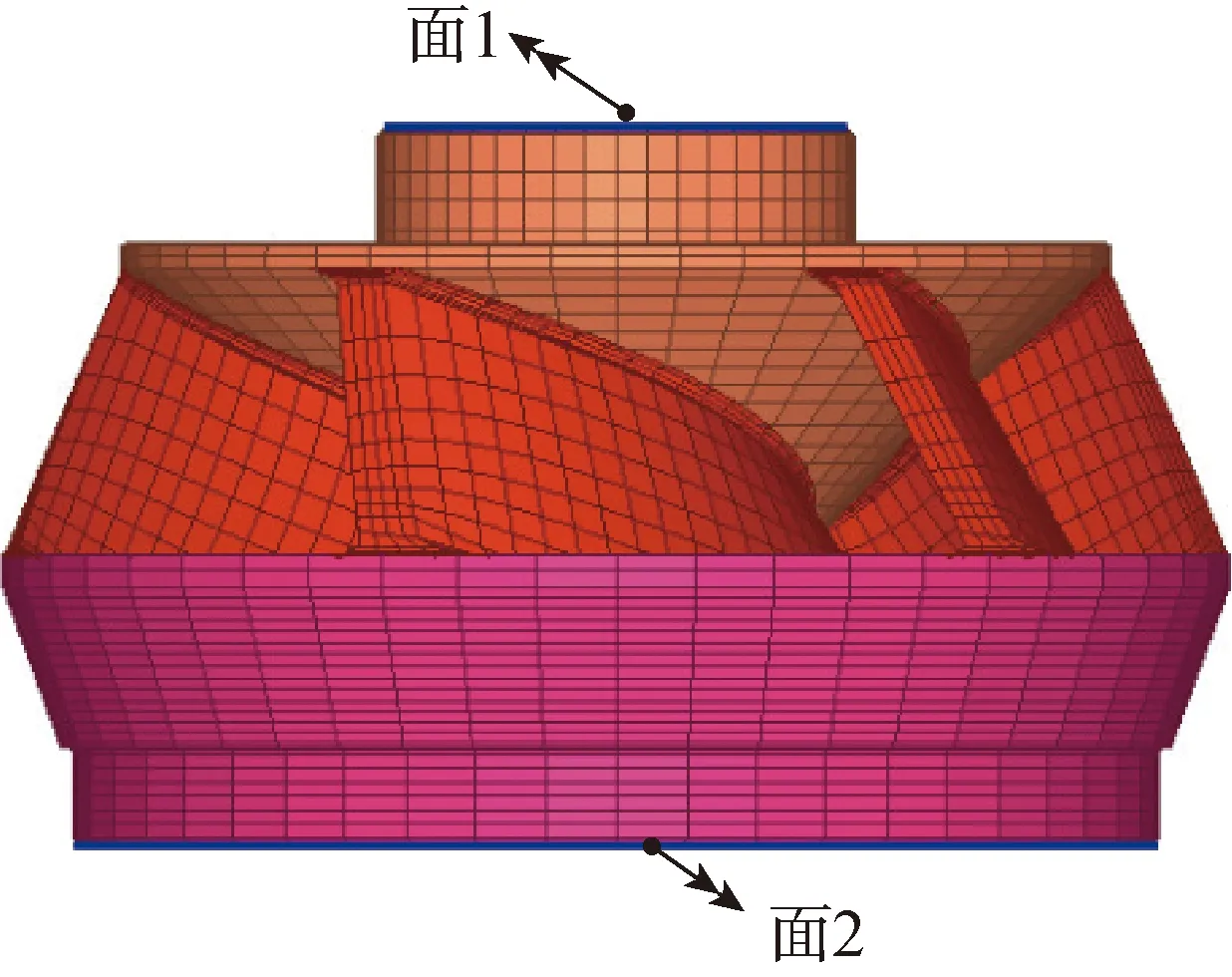
图2 叶轮有限元模型Fig.2 The impeller finite element model

(1)等效截面积计算

叶轮的有效元模型上施加下述载荷：

1)附着于面1上的节点全约束;

2)附着于面2上的节点施加载荷F。

(2)等效弯曲惯性矩计算

叶轮的有效元模型上施加下述载荷：

1)附着于面1上的节点全约束;

2)附着于面2上的节点施加弯矩M。

2.4 滑动轴承系数

主泵上导轴承及下导轴承为可倾瓦轴承，泵轴轴承为圆柱水润滑轴承，分别采用专用轴承计算软件计算轴承油膜刚度及阻尼系数,刚度及阻尼系数无量纲化后导入转子动力学计算软件MADYN2000，在计算时，计算软件将根据转子受力、转速等输入条件自动计算相应转速下的油膜刚度及阻尼系数。

在主泵的运行状态为热态、轴承最大安装间隙、电磁偏心磁拉力与叶轮径向水推力同向的条件下，轴承油膜刚度及阻尼系数随转速的变化曲线，请见图3。

图3 上导轴承刚度阻尼随转速变化曲线Fig.3 Upper guide bearing stiffness and dampingcoefficients variation along speed

图4 下导轴承刚度阻尼随转速变化曲线Fig.4 Lower guide bearing stiffness and dampingcoefficients variation along speed

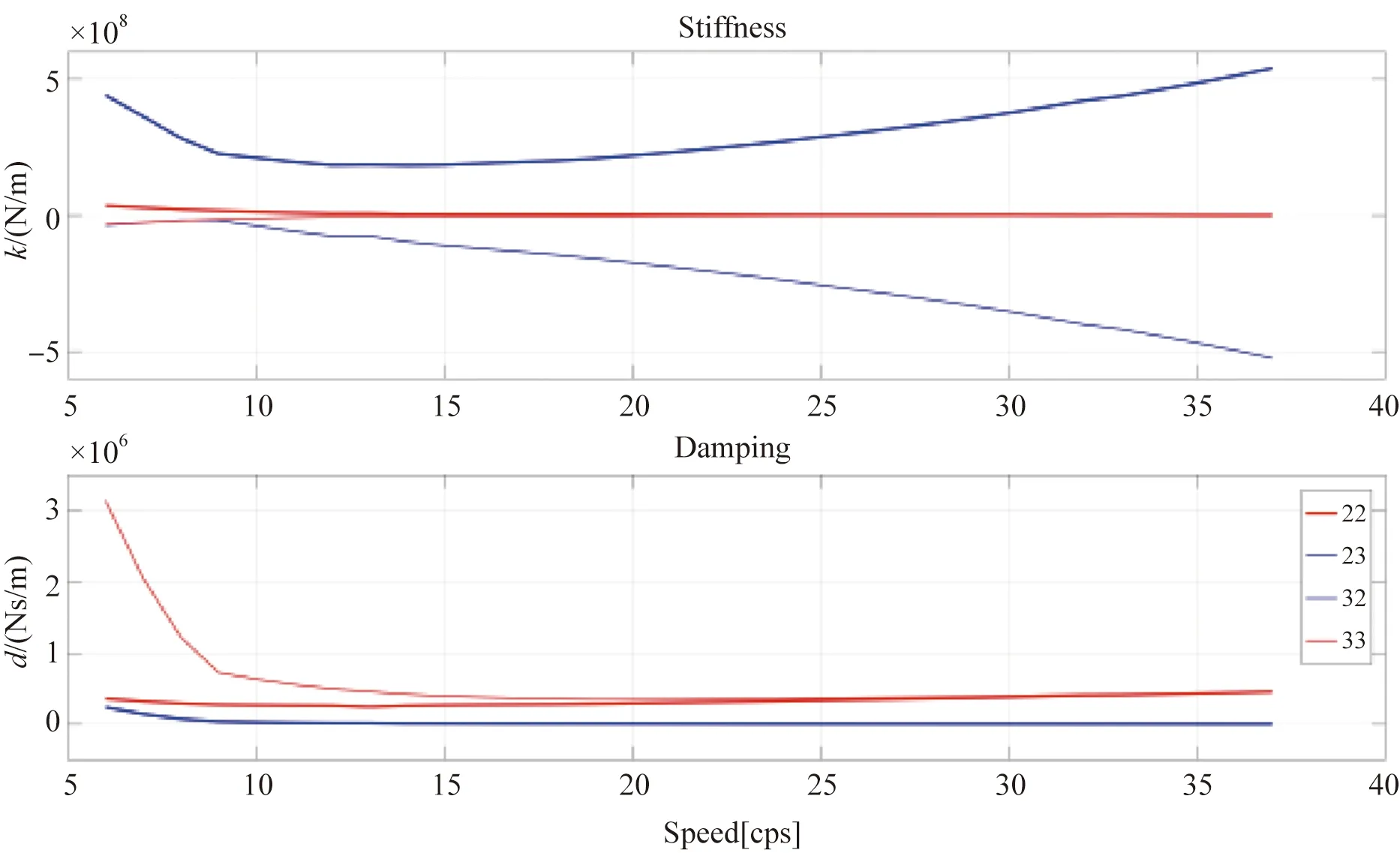
图5 泵轴轴承刚度阻尼随转速变化曲线Fig.5 Pump guide bearing stiffness and dampingcoefficients variation along speed

2.5 弹性支承

主泵轴承的支承机构简化为弹性支承，不考虑阻尼的影响，其支承刚度见图6。

图6 轴承支承刚度Fig.6 Bearing support siffness

3 计算结果

由于主泵的运行状态、轴承的安装间隙、叶轮位置的径向水推力及定转子间的偏心磁拉力方向的变化均会影响到滑动轴承的油膜刚度及阻尼，因此在对主泵的临界转速进行预测时，需要考虑上述所有因素影响。

在考虑主泵在热态、轴承最大安装间隙、叶轮径向水推力与电磁偏心磁拉力方向一致的条件下,主泵的临界转速在要求的运行转速范围内，前二阶临界转速分别是1 187.79 r/min以及1 304.10 r/min(见图7)。

4 临界转速评判标准

轴系稳定性主要是考查转子系统的临界转速，迄今为止，国内外尚无统一的考虑标准，目前，业界主要有下述几种考核标准：

(1)以理论临界转速计算为基础，对临界转速与工作转速之间的安全裕度进行规定，安全裕度通常考虑在10%～25%；辅之于对数衰减率对振动的稳定性进行判定。

该判定标准普遍应用于发电行业，比如：

1)低速水轮发电机转子系统;

2)汽轮机、汽轮发电机等。

在运用该标准时，通常是根据多年的经验，将轴承的支撑刚度考虑为恒定弹簧刚度或者刚性支撑，不考虑机组载荷以及运行条件等多方面的影响。对于常规的水轮发电机组、汽轮发电机等，该判定标准是偏保守的。

(2)对于石油、化学和气体工业用轴流、离心压缩机及膨胀机—压缩机在API617[1]标准中临界转速的定义是以转子响应曲线为基础，当放大系数 AF≥2.5的转速规定为临界转速；对此临界转速，是以隔离裕度SM为判定标准。

(3)以转子-轴承耦合系统为基础，考虑阻尼对振动的抑制作用，以阻尼系数为判定标准。

对于该标准，不同的行业或者不同的厂家根据各自的运行经验，对于临界转速对应的阻尼系数要求又各有不同。

1)对于石油、重化学和天然气工业用离心泵，API610[2]中规定见图7。

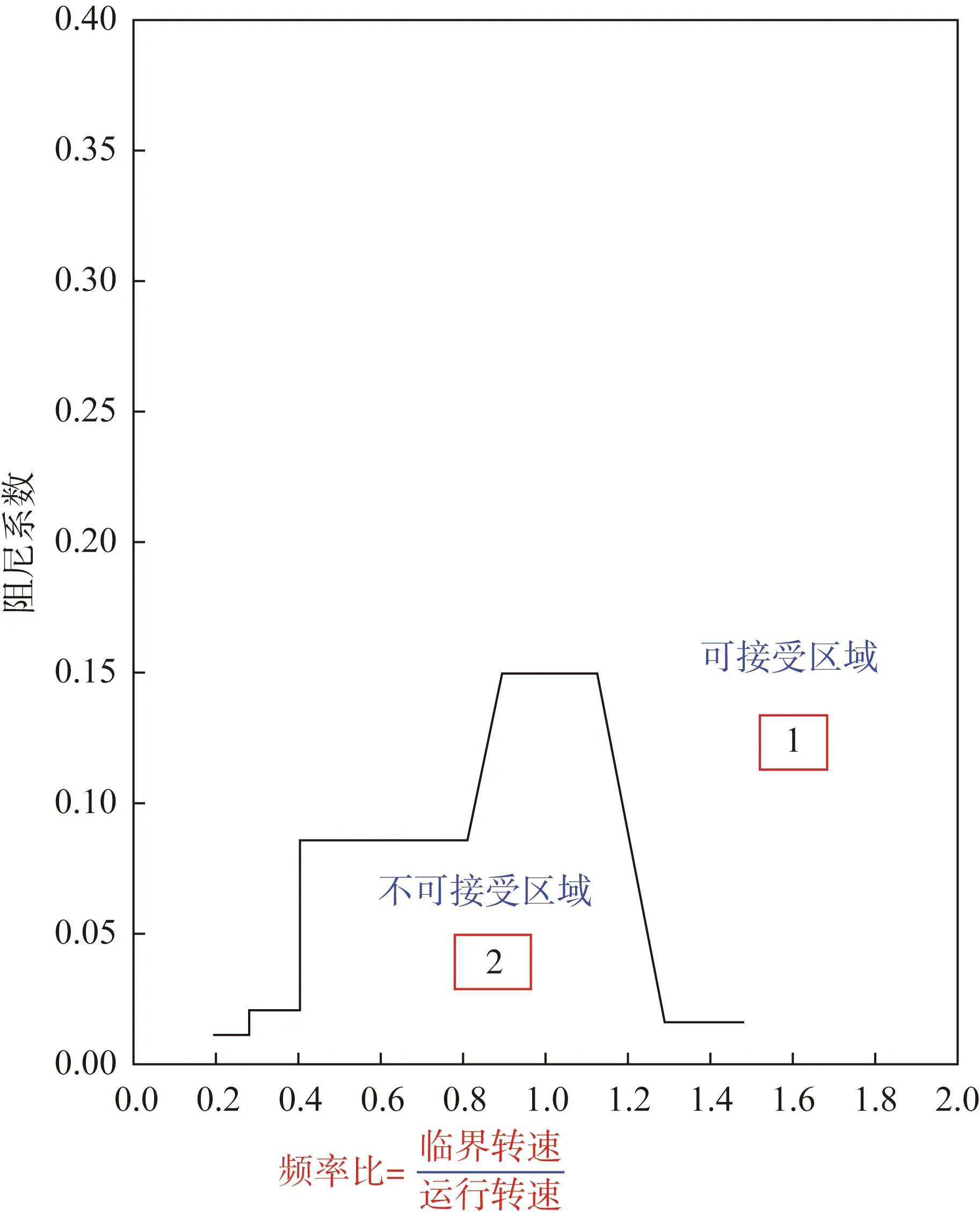
图7 API610 阻尼系数与频率比Fig.7 Damping coefficients and frequencyratio listed in API610

2)法国在借鉴API610的基础上，总结多年主泵运行经验，提出下述主泵临界转速判定标准，见图8。

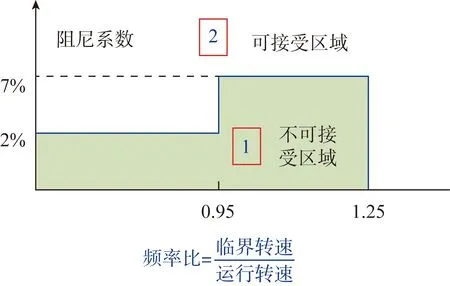
图8 阻尼系数与频率比Fig.8 Damping coefficients andfrequency ratio used in France

5 结论

在本文中，采用法国计算标准对临界转速进行判断，无论是第一阶的临界转速1 187.79 r/min还是第二阶临界转速1 304 r/min(见图9),其阻尼比均远高于法国标准中的规定值。

为了验证阻尼对主泵振动的影响，在考虑结构不平衡质量的基础上，还考虑了叶轮水力不平衡力的影响，对主泵进行了不平衡响应分析(见图10)，主泵在设计的连续运行转速范围内没有出现因临界转速而导致振动剧烈增大的情况，且其不平衡响应振动远低于设计振动标准。

因此主泵轴系在满足设计要求规定的阻尼比下，主泵能够安全稳定运行。

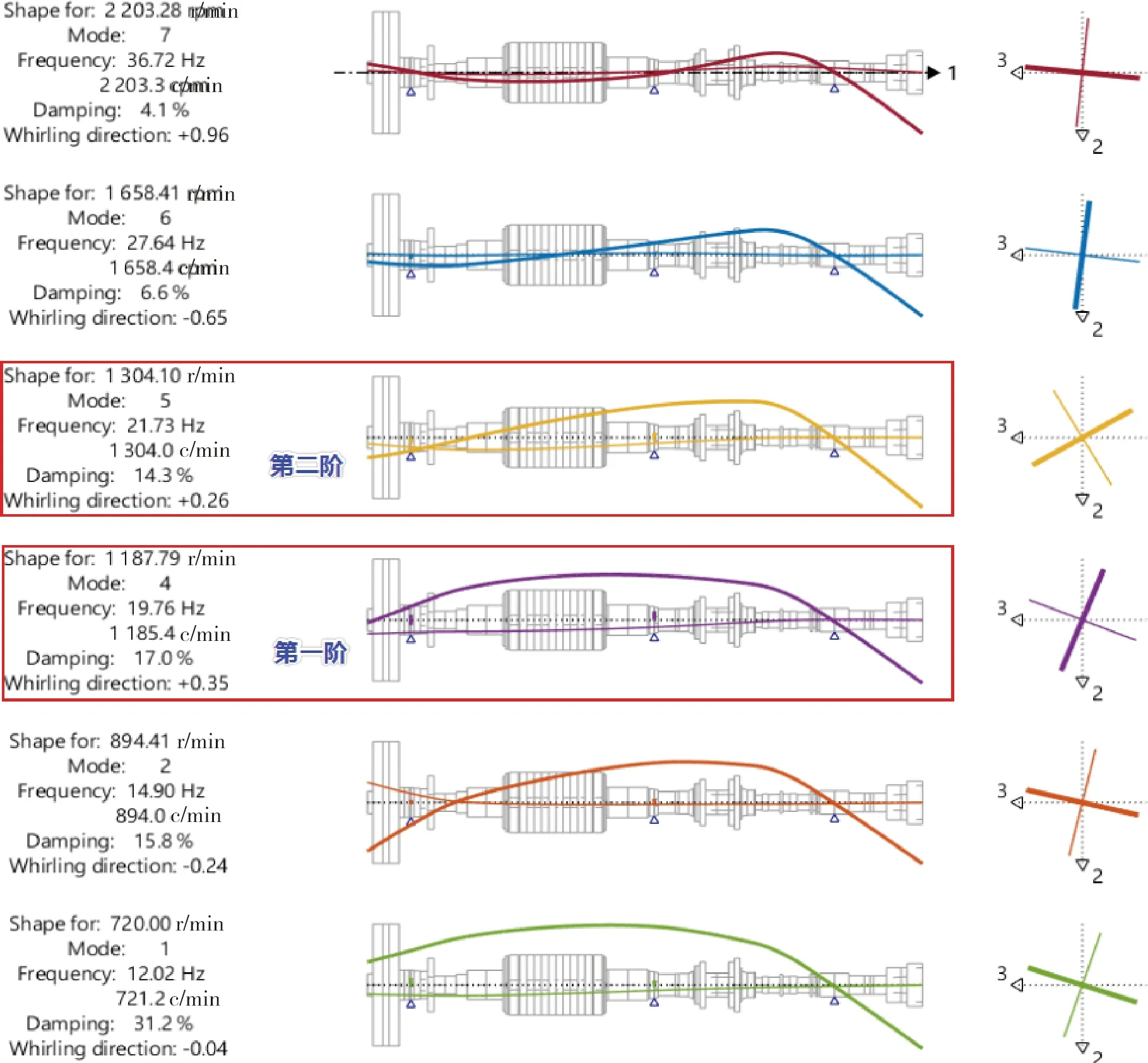
图9 主泵轴系临界转速Fig.9 Lateral critical speeds for reactor coolant pump

图10 主泵不平衡响应曲线Fig.10 Unbalance Response Curvesfor Reactor Coolant Pump