巧用辩证思维 提升解题能力
2020-12-17冯建国江苏省淮安市教学研究室223000
冯建国 (江苏省淮安市教学研究室 223000)
辩证思维方法是人们正确认识世界的媒介,是人们正确进行理性思维的方法.辩证思维方法是一个整体,它是由一系列既相区别又相联系的方法所组成的.数学解题既需要逻辑思维也需要辩证思维.归纳演绎、分析综合、具体抽象、历史和逻辑等辩证思维方法对数学解题有重要的指导作用.本文结合教学实践,对用辩证思维的方法培养学生数学解题能力作一探讨.
1 归纳和演绎:寻找解题的方向——到何处去?
归纳和演绎是最基本的思维方法.归纳是从个别上升到一般的方法,即从个别事实中概括出一般的原理;演绎是从一般到个别的方法,即从一般原理推导出个别结论.归纳和演绎的客观基础是事物本身固有的特殊和一般、个性和共性的关系.归纳和演绎是方向相反的两种思维方法,但两者又是互相依赖、互相渗透、互相促进的.
一般与特殊是对立统一的关系.解数学题时,有时会从特殊情况出发,通过推理解决一般问题;有时会从一般情况出发,通过一般结论来解决特殊问题.
例1在等差数列{an}中,已知S10=100,S100=10,求S110的值.
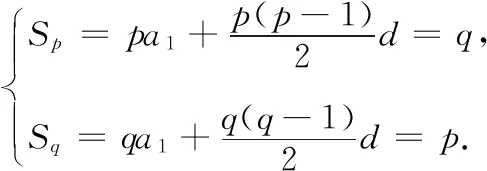
评析多数情况下特殊要比一般简单.但事物是辩证的,就本题而言,先考虑一般再考虑特殊反而是走了捷径.这是因为有时具体数的联系看起来并不比用字母表示来得清晰和简单.
2 分析和综合:寻找解题的路径——从何处来?
在数学解题过程中,分析一般是从目标出发,执果索因;综合一般是从条件出发,由因导果.分析与综合的关系既相互区别又相互联系,二者是对立统一关系.解数学题时,有时可以用综合法,有时可以用分析法,有时还可以将两者结合起来使用.
例2已知函数f(x)=lnx-x+1,g(x)=xex-2x(x∈(0, +∞)),求证:f(x)≤g(x).
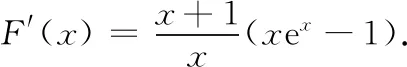
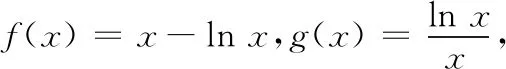
辩证思维告诉我们,在解数学题时既要关注问题的一般性,也要关注问题的特殊性,坚持具体问题具体分析,不能照搬照抄.
分析和综合是两种常见的思维方法.对一些较难的题目,往往会先分析后综合.又由于一些学生在使用分析法时会将执果索因写成由因导果,故提倡用分析法寻找思路,用综合法表述解题过程,有时也会将执果索因和由因导果同步进行,在中间寻找交汇点.总之,无论是分析还是综合,都是寻找解题路径的有效手段.
3 具体和抽象:寻找解题的策略——怎么做?
在数学教与学中,学生的数学学习要经历具体表象抽象的过程,教学时要在直观物体和抽象概念之间构建桥梁,从而引导学生把握事物最主要、最本质的数学属性. 抽象应有一个学生经历的过程,而不是直接告诉学生抽象的结果.数学抽象本身又是一个不断提高的过程,这一过程永无止境.
例3“石头、剪子、布”是大家熟悉的二人游戏,其规则是:在石头、剪子和布中,二人各随机选出一种,若相同则平局;若不同,则石头克剪子,剪子克布,布克石头.甲、乙两人玩一次该游戏,则甲不输的概率是.
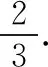
评析具体和抽象是两种常见的思维方法,决定解题的策略.在解决应用问题,特别是关于概率与统计的有关问题时,首先需要将实际的、具体的问题抽象为数学问题,然后再思考数学问题的解决办法.本题采用的方法是枚举法,体现具体本身也是解决问题的一种很好的思维方法.
4 历史和逻辑:寻找解题的原则——为什么?
逻辑指的是理性思维或抽象思维,它以理论的形态反映客观事物的规律性.历史包括两层意思:一是指客观事物的历史发展过程,二是指人类认识的历史发展过程.真正科学的认识是现实是历史发展的反映,要求思维的逻辑与历史的进程相一致.历史是逻辑的基础和内容,逻辑是历史在理论上的再现,是“修正过”的历史.逻辑和历史的一致是辩证思维的一个根本原则.
(1)联系法:就是运用普遍联系的观点来考察思维对象的一种观点方法,是从空间上来考察思维对象的横向联系的一种观点.
通常像递增与递减、升维与降维、有限与无限、连续与离散、运动与静止、正数与负数、展开与化简等都让人联想到某种联系.张景中院士认为:“一个事物的性质最终可以用一串数描述,它可以看成是一个有穷维或无穷维的以时间为自变量的向量值函数.事物的变化,无非是向量的各个分量的变化——增加与减少.”[1]增加与减少既相互区别又相互联系,二者是对立统一关系.在解数学题时,有时会从增加的角度来考虑,有时又会从减少的角度来考虑.
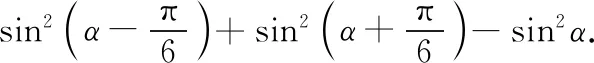
思路探求 原式中的三项都是正弦的2次幂形式,可以考虑降幂.
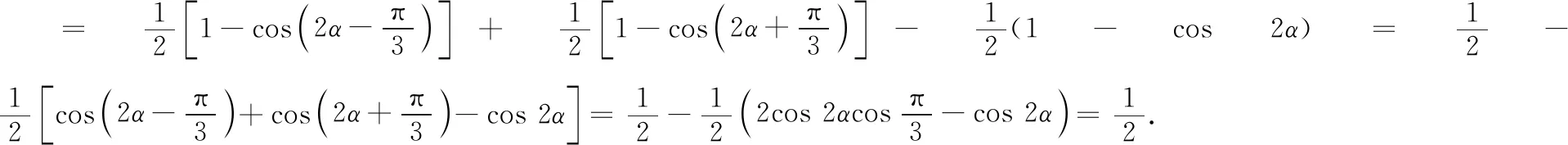
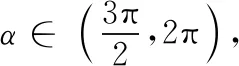
解题时通常采用的取导数法、取对数法、平面化法、坐标化法等都体现了联系的观点,而数形结合更是典型的代表.
(2) 发展法:就是运用辩证思维的发展观来考察思维对象的一种方法,是从时间上来考察思维对象的过去、现在和将来的纵向发展过程的一种方式.
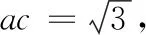
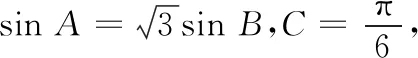
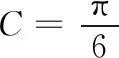
评析此类问题被称为结构不良问题,其特点是问题所给条件不全,解决问题必须另外补充条件,使得问题和解法均存在变数,问题是否有解与选择的条件密切相关.
(3)全面法:就是运用全面的观点去考察思维对象的一种观点或方法,即从时空整体上全面地考察思维对象的横向联系和纵向发展过程.换言之,就是对思维对象作多方面、多角度、多侧面、多方位的考察的一种观点或方法.
通常所说的直接与间接、分类讨论等是全面法的典型代表.解数学题时,有时要用直接法,有时要用间接法.解题的原则一般是正难则反,避实就虚.分类讨论就是将复杂问题进行分类,要求科学准确、不重不漏.
例6用2n(n∈N*,且n>1)个相同的元件组成一个系统N,前面n个元件串联成一个子系统A,后面n个元件并联成一个子系统B,再将两个子系统串联起来.各个元件能否正常工作是相互独立的,每个元件能正常工作的概率均为r(0 思路探求 对于子系统A,由于是串联,只要每一个元件都能正常工作方可,故系统A能正常工作的概率为rn.对于子系统B,正面考虑比较困难,可以采用间接法:不能正常工作的概率为(1-r)n,故能正常工作的概率为1-(1-r)n.于是整个系统N能正常工作的概率为P=rn[1-(1-r)n]. 评析求子系统A,B的概率时分别用了直接法和间接法.如果我们将子系统B中的n个元件也串联,然后再将A,B两个子系统并联,那么每个子系统能正常工作的概率都是rn.于是系统N能正常工作的概率为P=rn(2-rn).这里用直接法和间接法都可以.若用直接法,需要考虑3种情况;若用间接法,则需考虑1种情况.其本质就是不重不漏的分类讨论,前者体现不同思维角度的全面,后者体现同一种方法的全面. 总之,辩证思维蕴含的对立统一规律对数学解题具有很强的指导作用,无论是解题的方向、路径,还是解题的策略、原则.为了适应核心素养导向的新高考,提升学生的核心素养势在必行,而通过辩证思维提高学生的数学批判质疑能力,也是体现突出核心素养导向的重要策略之一.为此,教师需要在数学解题教学中引导学生多用辩证的思维方法解决问题.
