一种改进预测模型在高铁变形分析中的应用

赵云强

(中国铁路设计集团有限公司，天津 300251)

变形监测的目的是掌握工程建筑和地质构造的稳定性，以便为施工安全诊断提供必要的信息，并为后期工程管理提供相应的数据支持[1]。 由于高速铁路的沉降变形量较小，且观测过程中随机噪声会对高铁沉降变形预测和数据质量分析造成较大影响。 因此，为了掌握高铁沉降变形规律，并对其未来的变形趋势做出准确预判，需要建立一种合适的算法模型，以便达到准确的预测结果[2-3]。 已有许多学者进行了相关研究，文鸿雁等将小波去噪与GM(1，1)模型组应用于高铁线下工程，认为用小波去噪处理后的数据建立GM(1，1)模型模拟精度和预测效果较好[4]。 陈晨等将卡尔曼滤波和GM-AR 组合模型运用到高层建筑物沉降变形中，认为该方法可减弱观测噪声对数据分析的影响，提高监测值的预测精度[5-6]。 雷孟飞等将自适应卡尔曼滤波运用到BDS 变形监测数据处理中，认为自适应卡尔曼滤波对粗差的剔除效果明显优于普通卡尔曼滤波，并且能够保留被监测物的真实位移[7-8]。

目前，在高铁沉降变形中运用组合模型分析的案例较少，而高铁沉降变形监测成果精度要求较高。 因此，在前人研究的基础上，提出了一种适用于高铁沉降分析的新方法，其主要思想为:选择经典卡尔曼滤波与方差补偿自适应卡尔曼滤波两个不同算法中滤波效果较好的对原始数据进行消噪处理，然后利用GM(1，1)-AR 模型对滤波值进行建模预测。

1 组合模型算法理论

1.1 卡尔曼滤波算法

经典卡尔曼滤波算法可以用如下两个方程表示

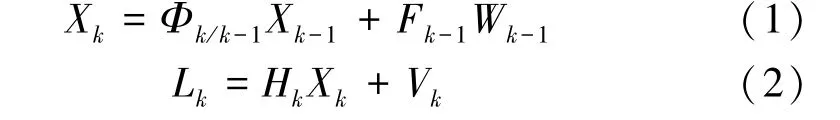
式中，Xk为状态向量(n 维)；Lk为观测向量(m维)；Φk/k-1转移矩阵(n×n)；Wk-1动态噪声(r 维)；Fk-1为动态噪声矩阵(n×r)；Hk为观测矩阵(m×n)；Vk为观测噪声(m 维)。

根据最小二乘原理，可以推得离散随机系统的卡尔曼滤波递推公式，一步预测值为

在给定了初始值^X0、^P0后，就可以运用式(3)～式(7)进行卡尔曼滤波递推公式计算，实现滤波以及有效剔除随机误差干扰噪声的影响。

方差补偿自适应卡尔曼滤波的基本原理用公式表示如下。

假定有正态序列{Ωk}和{Δk}，X0是正态向量，则定义i 步预测残差为

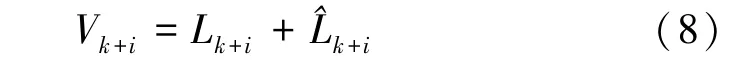
式中，Vk+i表示预报残差，Lk+i为第k+i 期的观测值，^Lk+i是Lk+i的最佳预测值。

若 在 观 测 时 间 段 tk+1， tk+2… tk+N内， 假 定DΩr-1Ωr-1为常值对角阵，记

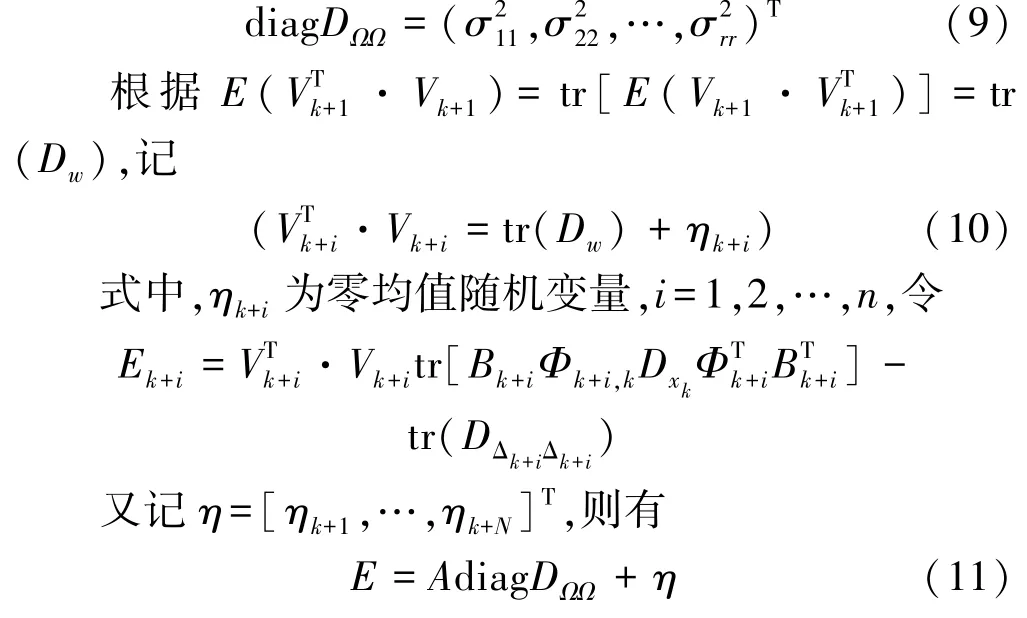
式(11)是关于diagDΩΩ的线性方程组，当N≥r 时有唯一解，有

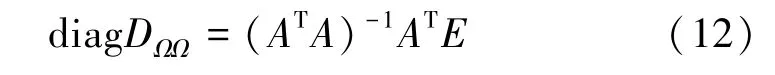
根据上述各式，可求得任意长度时间段的DΩΩ作为动态噪声协方差阵的实时估计[8-11]。

1.2 GM(1，1)模型

在研究少数据、小样本、贫信息等不确定性问题上，GM(1，1)模型有着极大的优势[12-13]，原理如下。

若有一组非负的初始时间序列可以表示为x(0)(k)={x(0)(1)，x(0)(2)，…，x(0)(n)}，其中，n 为序列长度，k=1，2，…，n。 第一次累加该原始序列后生成序列(1-AGO)

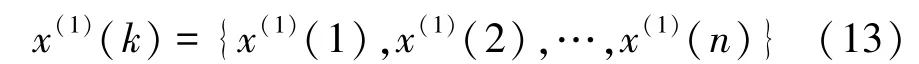
对式(13)进行时间求导，得到GM(1，1)模型的影子方程

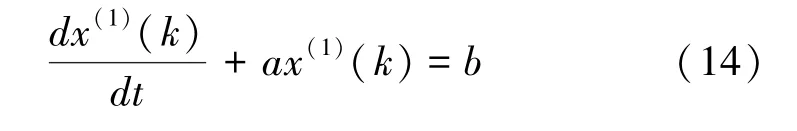
式中，a、b 为待定系数，a 称为发展灰数，b 称为灰作用量。 方程(9)求解，可得到影子方程的时间响应式，即

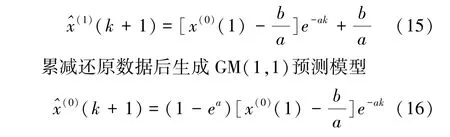
1.3 AR 自回归模型

设时间序列{yk}具有正态、平稳、零均值的特性[14-15]，其自回归模型为

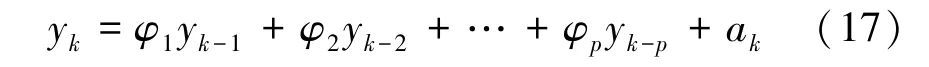
式中，φ1，φ2，…，φp是自回归模型参数，ak为白噪声序列，p 为模型阶数。

令k=p+1，p+2，…，N，则

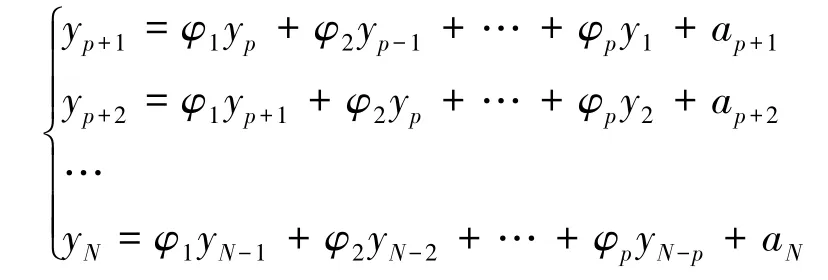
对p 取值(正整数)，令p=1，2，…n，可得到AR(1)，AR(2)，…，AR(n)。

AR 模型的参数采用最小二乘法估计，对模型阶数p 的确定采用最小信息准则(AIC)，即

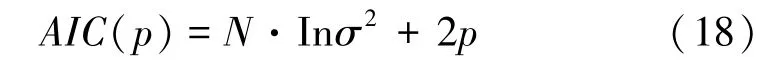
式中，p 为序列数据总个数，使式(8)值达到最小所对应的p 为最佳阶数，p 值一般不大于5，σ2为各阶数对应的残差方差。

1.4 基于方差补偿自适应卡尔曼滤波的GMAR 模型

基于方差补偿自适应卡尔曼滤波的GM-AR 模型算法的研究思路为:对比分析经典卡尔曼滤波与方差补偿自适应卡尔曼滤波两个不同算法对高铁沉降监测值消噪的适用性，选取其中效果较好的方法对原始观测数据进行滤波消噪处理，获取有效地变形量，然后利用GM(1，1)模型对滤波值进行建模预测，提取其中的趋势项，最后利用AR 时间序列模型对残差序列进行建模预测，并与单一的GM(1，1)模型和GM(1，1)-AR 模型的预测结果进行对比分析，以此得到新模型的预测精度以及可靠性。

2 工程实例分析

2.1 实验案例简介

高速铁路沉降监测中布设的监测点较多，监测数据量较大。 以某工程队在其项目标段内的高速铁路L052 号监测点共30 期的观测数据为实验对象，原始观测值如表1 所示。

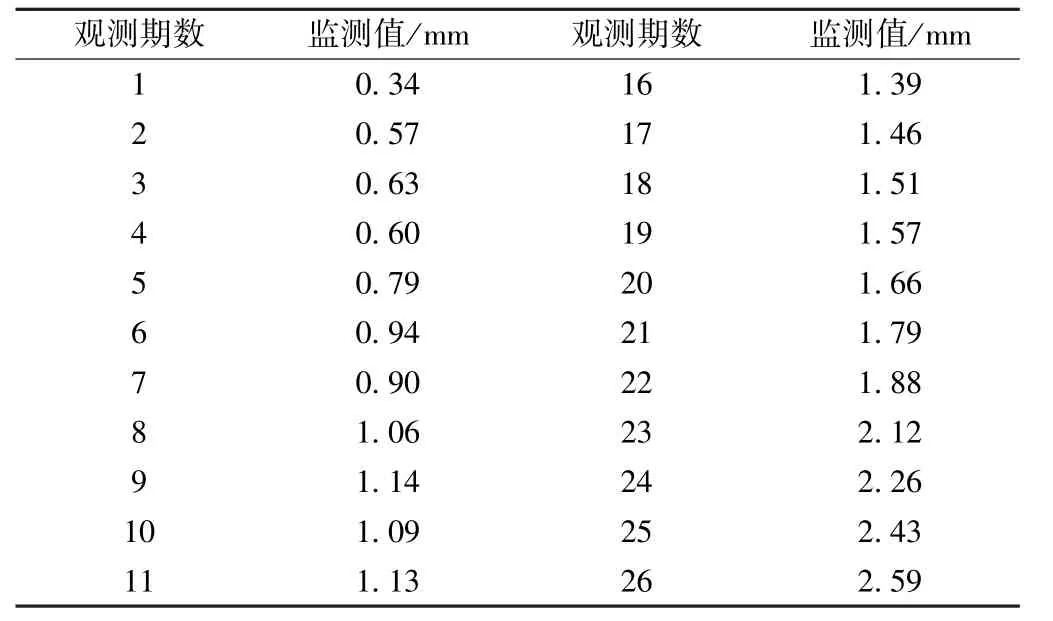
表1 L052 号监测点前20 期沉降监测值

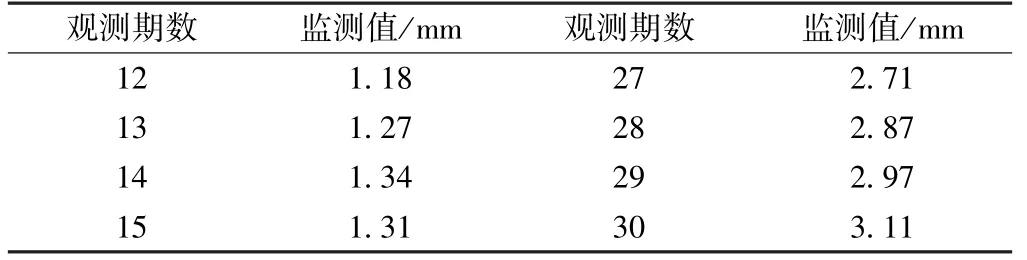
续表1

研究步骤为:①采用经典卡尔曼滤波与方差补偿自适应卡尔曼滤波分别对L052 号监测点前10 期的实际观测数据进行滤波处理，选取滤波效果较好的一组数据作为该点实际变形值；②对实际变形值采用GM(1，1)-AR 模型进行建模后再对其后20 期数据进行模型预测，得到其预测值，再根据实际监测值与预测值的残差大小来检验预测结果的可靠性。

2.2 两种滤波方法结果比较

此次实验中，卡尔曼滤波模型的状态参数采用L052 号监测点的初始位置和沉降速率，动态参数采用加速度，以此确定观测噪声协方差阵DΔ(0)= 2，动态噪声协方差阵为DΩ(0)= 0.5，滤波初始值为X(0)=[0.34，0.002 3]T，DX(0)=图1 和表2 为不同滤波方法对监测点前10 期实测数据的滤波结果。

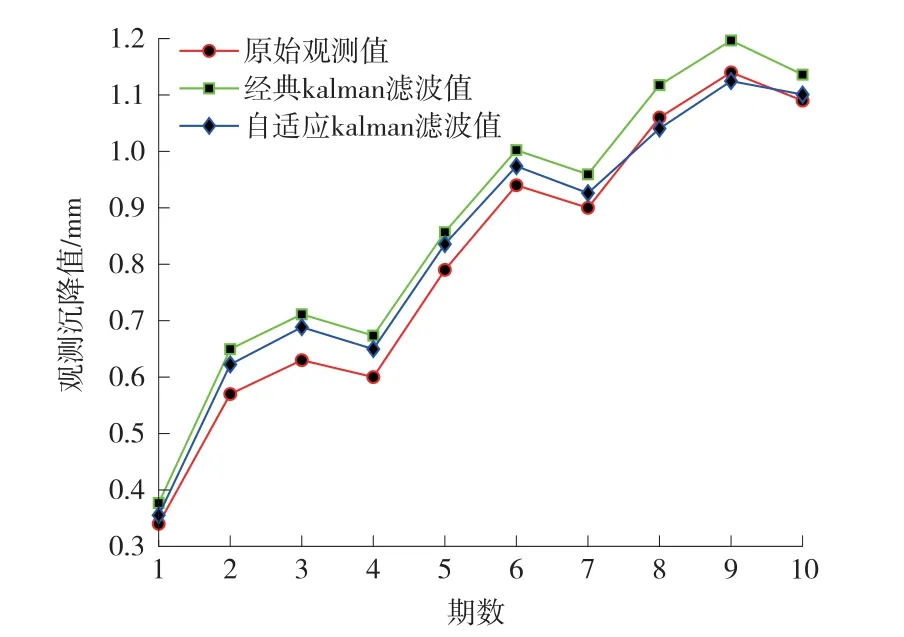
图1 不同滤波方法结果对比

表2 L052 号监测点沉降值与滤波值比较 mm

根据表2 中的结果，计算出两种不同方法的信噪比和均方差，结果如表3 所示。

表3 两种滤波方法精度对比

从表3 中可以看出，方差补偿自适应卡尔曼滤波较经典卡尔曼滤波信噪比大，但均方差小，这说明前一种方法对于误差的剔除效果要优于后一种方法，且监测数据曲线的整体变化趋势更加平稳。 因此，选择方差补偿自适应卡尔曼滤波算法的滤波结果作为L052 号监测点的实际变形值来进行后续的建模和预测。

2.3 建模预测与精度评定

在2.2 节中得到监测点实际变形值的基础上，采用GM(1，1)灰度模型对其进行建模后得到相应的残差序列，利用AR 模型对残差序列进行建模，再预测该监测点后20 期的变形数据。 同时，以前10 期未经滤波的实测值为基础，分别采用GM(1，1)、GM(1，1)-AR 模型进行建模，同样对后20 期数据进行预测。 预测结果如表4 所示。

3 种不同方法的预测结果如图2。

3 种模型预测精度比较见表5。

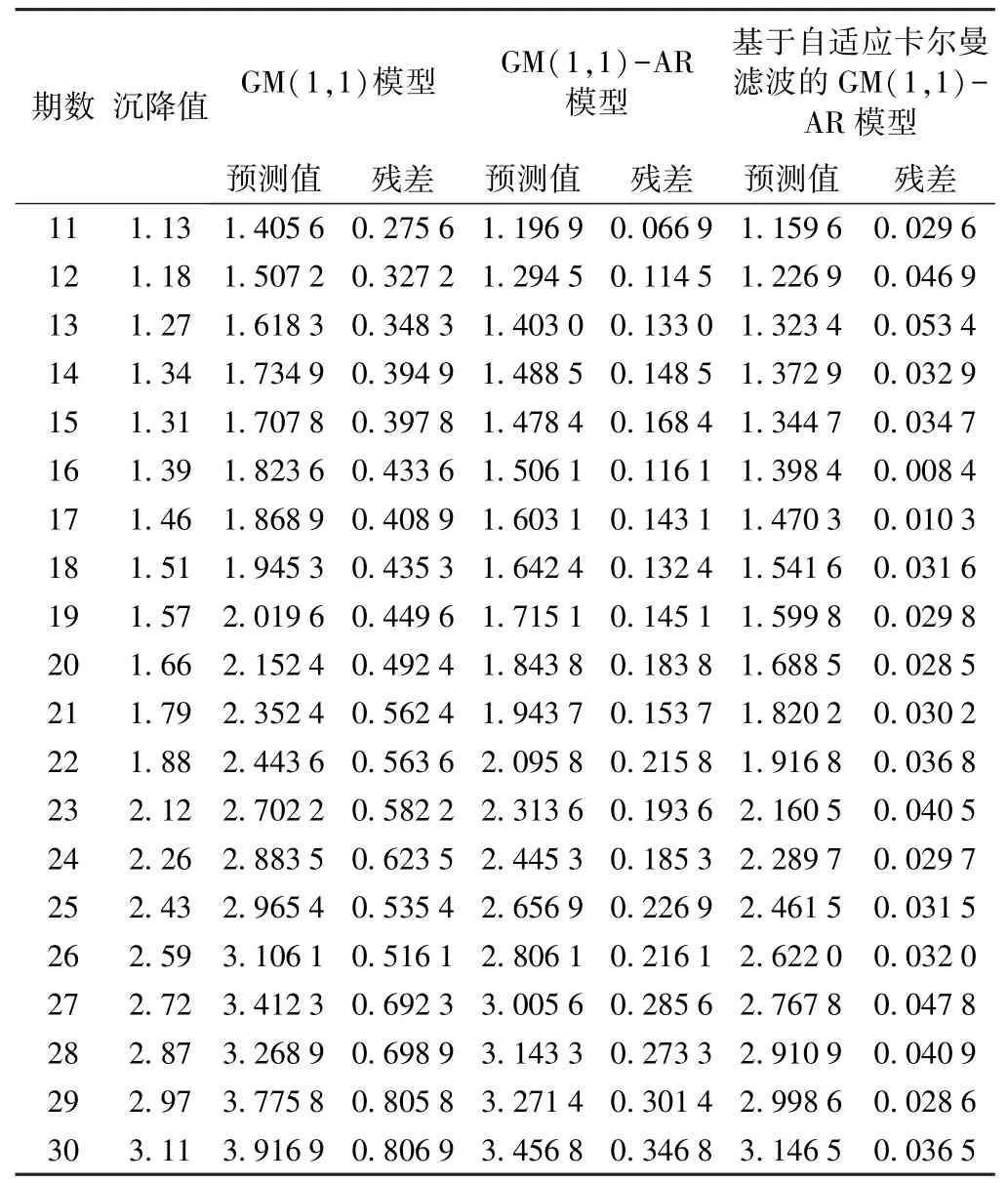
表4 不同方法预测结果比较 mm

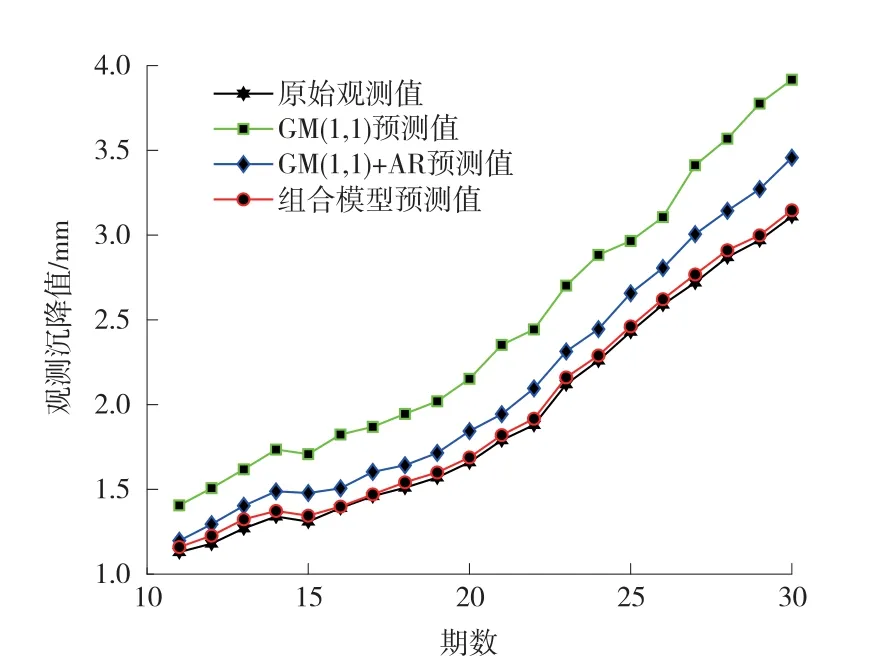
图2 不同方法预测结果

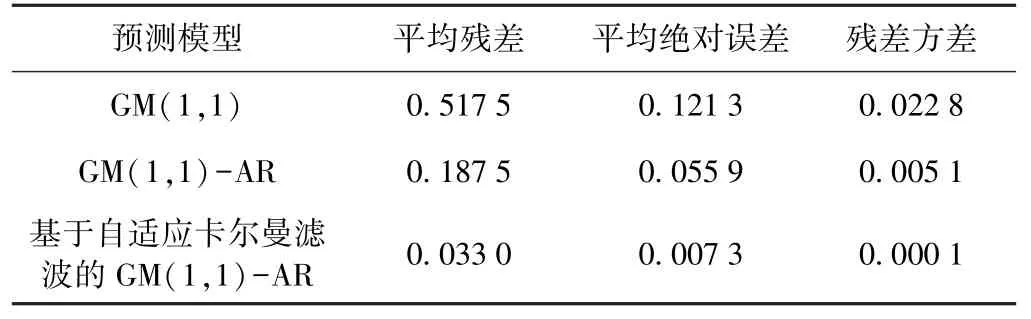
表5 不同方法预测精度比较 mm

从图2 中可以看出，GM(1，1)模型的预测值的曲线走向与实际监测值的曲线走向差距最大，基于方差补偿自适应卡尔曼滤波的GM(1，1)-AR 组合模型的预测值的曲线走向最接近实际监测值的曲线走向，且曲线也更为平滑。 由此可见，相比两种较单一的模型，组合模型随着时间的推移，更接近实际值。

从表5 中可以看出，新方法得出的预测值的平均残差、平均绝对误差、残差方差分别为0.033 0 mm、0.007 3 mm、0.000 1 mm，且平均残差、平均绝对误差、残差方差分别为 GM(1，1)、GM(1，1)-AR 模型的6.4%、6.0%、0.5%、17.6%、13.1%、2.1%，其预测精度远高于GM(1，1)、GM(1，1)-AR 模型，且较文献[5]与文献[6]中得到的平均残差、平均绝对误差以及残差方差更小。 由此可见，相较于经典卡尔曼滤波算法，方差补偿自适应卡尔曼滤波算法对沉降曲线中波动较大的点的滤波效果明显较优，曲线整体平稳性更好，且相较于另外两种预测模型，新组合模型预测精度更高，预测结果也更接近真实值。

3 结论

(1)在高铁变形监测分析中，方差补偿自适应卡尔曼滤波算法相比经典卡尔曼滤波算法，其信噪比较大，均方差较小，其曲线变化也更为平稳。 说明方差补偿自适应卡尔曼滤波结果精度更高，效果更好，可在很大程度上削弱随机误差的干扰。

(2)基于方差补偿自适应卡尔曼滤波的GM(1，1)-AR 组合模型对高铁监测点变形值的预测精度远高于其余两种模型，且其预测值的变化趋势很接近实际监测值的变化趋势。

(3)基于方差补偿自适应卡尔曼滤波的GM(1，1)-AR 组合模型在一定程度上汲取了3 种模型各自的优势，突破了利用单一模型进行变形预测的局限性，在高铁建设阶段的变形监测实例分析中具有一定的运用价值。