基于车载移动测量系统的盾构隧道检测方法

巩 健

(中国铁路设计集团有限公司，天津 300251)

随着城镇化的快速发展，地铁已成为衡量城市可持续发展水平的重要指标，对解决城市中愈发严重的交通堵塞问题具有重要意义[1]。 盾构法由于机械化程度高、作业速度快、对周围建筑物影响小等优势[2]，在地铁隧道施工建设中被广泛采用。 然而，受复杂的地质条件、周边建筑物荷载和土体扰动、周边工程施工、列车运行振动等众多因素影响[3]，隧道盾构管片常出现上拱、下沉、内鼓和裂缝等各种结构病害，成为影响地铁正常运营的重大安全隐患。 因此，在地铁修建、竣工及运营过程中，隧道结构检测已成为日常监护的重要内容。 根据《城市地下空间检测监测技术标准》关于盾构法隧道结构检测的相关规定，需要对隧道断面椭圆度和水平直径进行检测[4]。 传统人工检测手段作业效率低下，受人为误差影响大且只能获取局部的数据，已难以满足现代工程的检测需求[5]。 近年来，移动三维激光扫描技术使得这项工作变得更加便捷高效[6-7]。 众多学者利用点云数据进行隧道断面椭圆拟合方法的研究。 琚俏俏将去噪后的断面点云代入椭圆公式，通过求解线性方程组获得椭圆参数[8]；李维涛通过代数拟合法利用至焦点和距离不变迭代计算椭圆参数[9]。 但是以上方法计算较为复杂且去噪效果较差，容易产生局部拟合现象从而导致拟合结果偏差较大等问题。 因此，提出采用截尾最小二乘计算椭圆参数的最优初值，再通过选权迭代逐步抑制噪声和粗差的影响，获得椭圆参数最优估值的方法。

1 点云采集与误差分析

1.1 点云采集

车载移动测量系统通过将激光扫描仪搭载于配置有里程计、惯导测量单元、控制机等组件的小车载体上[10]，通过人力或电力驱动小车沿轨道平行于隧道线路方向前进。 在此过程中，扫描棱镜采用线扫描模式，垂直于隧道内壁高速旋转并发射密集的激光脉冲(如图1)，通过测量每个激光脉冲发射后经被测物体表面再返回仪器的时间差(或相位差)来计算距离S，同步测量每个脉冲激光的横向扫描角度α、纵向扫描角度θ以及反射强度I，即可获得任意扫描点的三维坐标(见图2、式(1))。

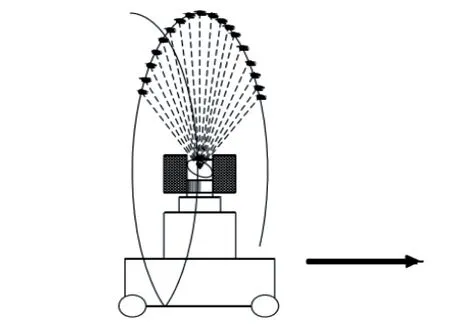
图1 车载移动测量系统作业原理

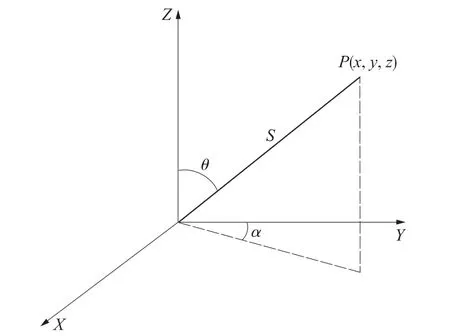
图2 扫描点坐标计算示意

扫描仪自身没有记录运动轨迹参数的能力，假定扫描的点云数据在其自身坐标系内是重叠的。 在后处理阶段，将惯导数据和里程计数据进行组合，解算得到扫描系统的运行轨迹，再将点云数据与运行轨迹根据时间信息进行融合，即可将扫描数据转换为与隧道结构和线型一致的三维点云数据。 结合小车启动时的初始里程，即可得到隧道指定里程处的正交断面点云。

1.2 误差分析

移动式扫描获取的点云轨迹为密集的螺旋线，根据里程信息提取指定位置的正交断面点云时，主要存在两类误差:螺旋线误差和转向误差。

螺旋线误差如图3 所示，BC 代表标准正交断面，AD 为实际提取断面，令隧道内半径为r，螺旋线间距为L，则螺旋线误差可表示为

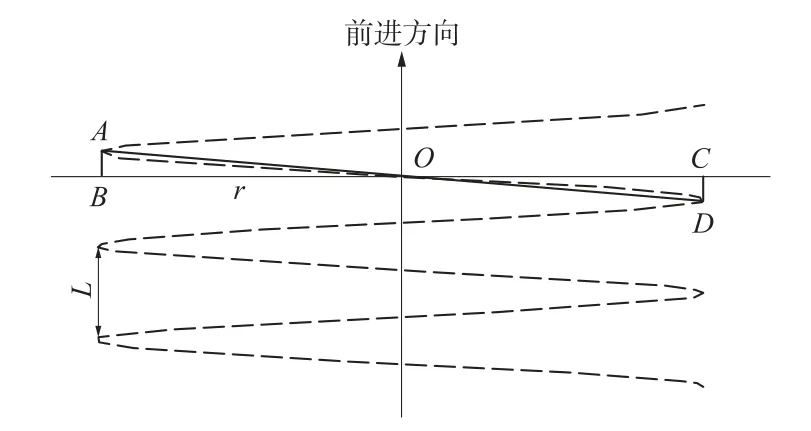
图3 断面点云螺旋线误差

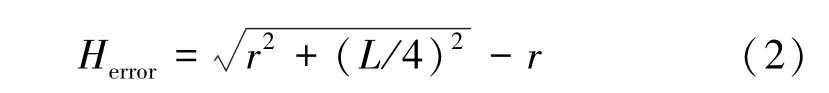
小车一般按照约2 m/s 的速度作业，扫描仪的线扫频率为200 Hz，则螺旋线间距L 为0.01 m。 隧道内半径r 通常为2.7 m，根据式(2)计算得到螺旋线误差为0.001 2 mm(可忽略不计)。

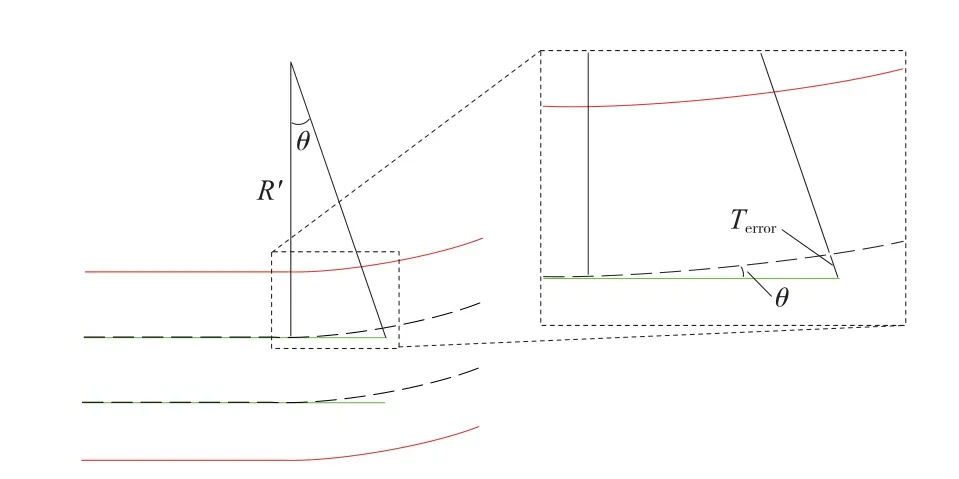
图4 轨道位置误差

轨道位置误差(Terror)如图4 中红色线段所示。 在隧道转弯处，受轨道位置安装偏差的影响，轨道与隧道之间不再保持平行，会存在一个角度偏差θ，有

其中，R′表示隧道转弯半径。

受角度偏差影响，实际提取的断面PN 会与标准正交断面QM 存在一定的转向偏差Serror(见图5 中红色线段)，有

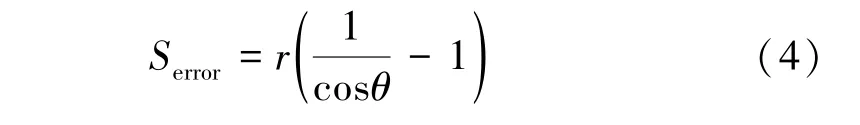
其中，r 表示隧道内半径。

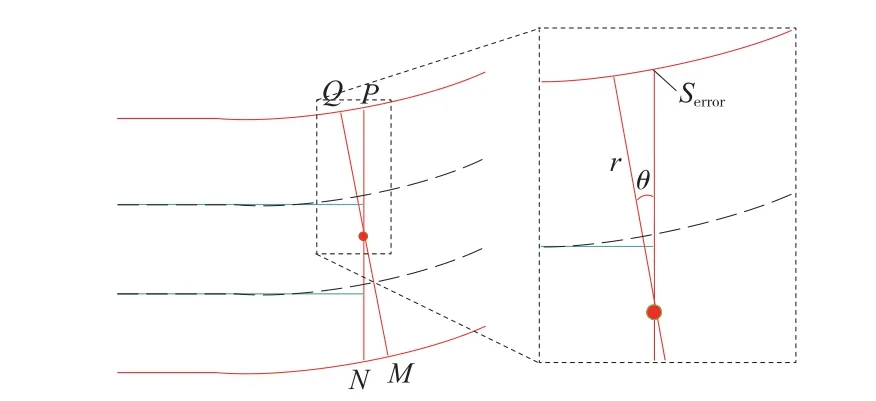
图5 断面点云转向误差

假设轨道位置误差为0.01 m(实际在轨道精调后仅为毫米级[11])，隧道转弯半径按2 000 m 计算，则角度偏差为0.18°，相应转向误差Serror为0.013 mm(可忽略不计)。 基于以上误差分析，提取的隧道断面可视为正交断面，在后续断面拟合精度验证时，可不考虑上述误差带来的影响。

2 椭圆拟合

隧道断面椭圆拟合是进行收敛变形分析的基础。隧道衬砌内壁附着的管线、照明、疏散平台等设备[12]，以及隧道中的灰尘和杂质会导致断面点云数据中存在大量的干扰信息(图6 中红色点)，致使拟合参数不理想，无法获取最佳拟合效果，在处理时应予以抵抗或去除。

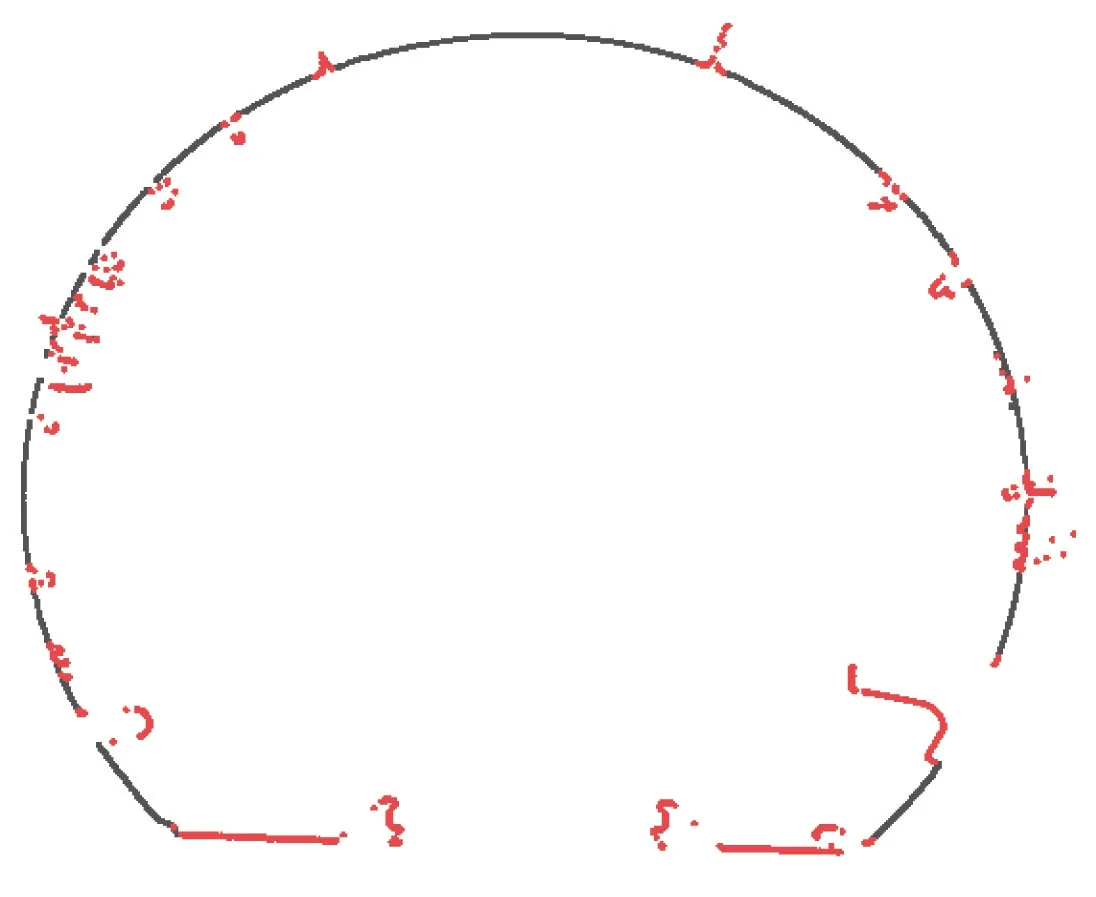
图6 隧道断面点云

2.1 截尾最小二乘法估计

普通最小二乘法(Ordinary Least Square，OLS)是常用的回归模型估计方法，但是其使用的前提是随机误差服从正态分布(即高斯分布)。 对于非正态分布(尤其是长尾分布)的随机误差，即使观测值中仅存在极少量的异常数据(离群点)，OLS 也会极度敏感，并对拟合结果产生破坏性影响。

隧道断面点云数据中存在的粗差点或噪声点等干扰信息是非正态分布的，在使用OLS 进行椭圆拟合之前，需要耗费大量时间进行滤波去噪等预处理工作，对其处理效果也有较高的要求，处理不彻底时，拟合参数会产生较大的偏差。

截尾最小二乘法(Least Trimmed Squares，LTS)是一种具有高崩溃点的稳健估计方法[13]，能够很好地检测并抵御异常数据对于回归分析的不良影响，即使在噪声和粗差含量较高的情况下，也有较好的拟合效果。其定义为

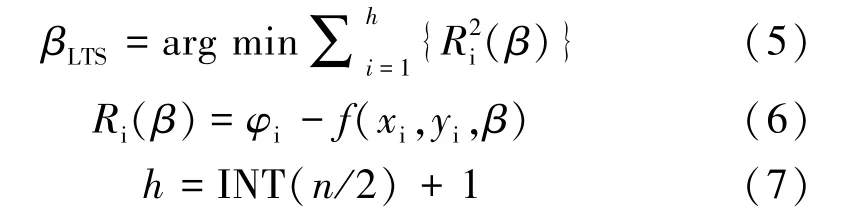
其中，βLTS为待求估计参数的最优解，Ri(β)为观测值φi与估计值f(xi，yi，β)的残差，n 为参与估计的数据点数量，常数h 表示n 的一半。

当n 和h 较大时，庞大的计算量会导致截尾最小二乘估计的计算效率较低。 因此，需要采用一种快速求解方法，其基本思想是从n 个观测值中抽取m 组样本，每组样本随机包含k 个观测值，利用k 个观测值解算最小二乘估计值β。 然后计算n 个观测值在β 下的残差平方(β)(i=1，2，…，n)，将其升序排列，记前h个残差平方和为βLTS，取所有组合中βLTS最小的对应解作为LTS 估计的准确解。

截尾最小二乘估计虽然可以抵抗观测值中较大含量的粗差，但是样本中观测值随机采样的准确性无法保证。 具体来说，根据椭圆方程(式(8))可知，随机采样至少需要5 个点，才可以解算椭圆参数。 当任意选择的5 个观测值分布不均或集中在一侧时，会导致局部拟合情况的出现。 因此，将断面点云按照角度等分为5 部分(见图7，下侧包含轨道部分不参与计算)。线扫描模式的点云为有序排列，按角度划分也可简化为按点号间隔划分。 断面点云数量以8 000 点为例，除去轨道部分后的点云序号为660 ～7 340，五等分即660～1 993，1 994 ～3 327，……等。 在每个部分分别选点参与计算，这样可以保证选取的点云初值接近于最终的椭圆方程。

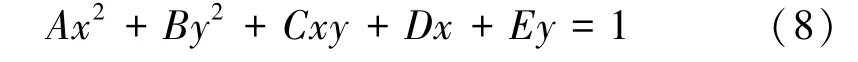
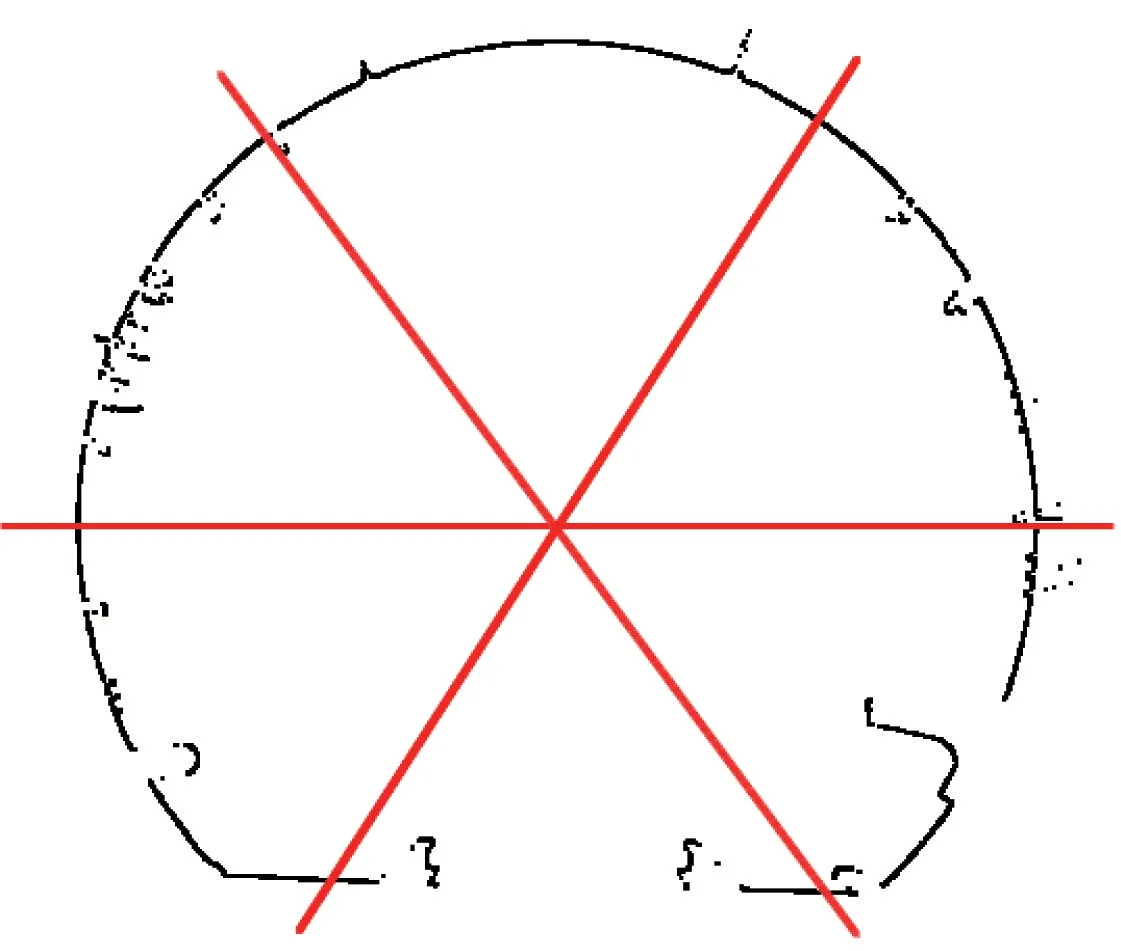
图7 断面点云等分示意

在5 个部分的点云中分别随机选取1 点构成一组点集通过式(9)参与拟合，有

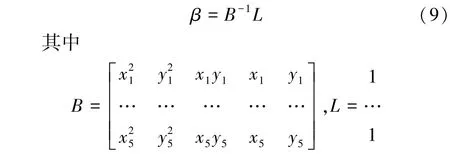
解联立方程组可得到拟合参数β0=[A0B0C0D0E0]T。

设置重复抽样数m 为每部分点云的数量，计算每组样本的拟合参数(i=1，2，…，m)对应的n 个观测值的残差平方，将其升序排列，取前h 个残差平方和最小的一组参数记为βLTS，并将其作为拟合初值。

2.2 选权迭代

在得到椭圆拟合初值βLTS的情况下，为减少隧道内壁噪声与粗差点对拟合效果的影响，采取选权迭代的方式将其逐步消除，以此来获得拟合参数的最优解，列出间接平差误差方程

在改正数矩阵V 中，粗差与噪声的数值会偏大。利用这一特性，当观测值改正数大于1.5σ 时，将权按照式(13)调整；当大于3.0σ 时，令权为0。 将调整后的权阵P 重新代入法方程中迭代计算，直至满足设定的迭代次数或小于设定的阈值时停止。

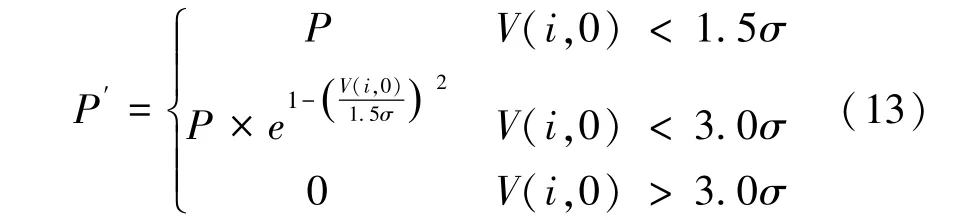
2.3 计算椭圆度和水平直径

椭圆度是定量分析隧道断面整体变形的重要指标。 通过上述过程计算得到的椭圆参数，根据式(14)可获得拟合椭圆中心的坐标(xc，yc)

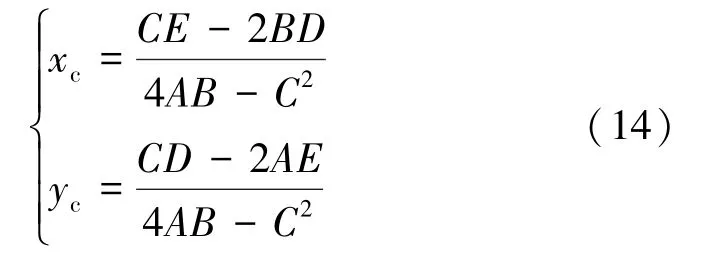
椭圆的长轴a、短轴b、偏转角θ 以及椭圆度ω 按下式计算

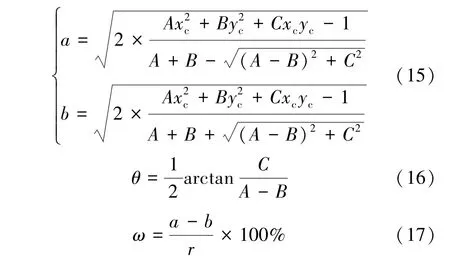
其中r 为隧道的标称内半径。

除椭圆度外，隧道结构检测中还比较关心盾构环水平方向的直径与设计直径的差值。 由于上述椭圆拟合方法获取的是全部点云(除轨道部分)的整体最佳拟合参数。 因此，在局部可能会存在较小的拟合偏差。如果直接采用拟合的椭圆计算盾构环水平直径，计算结果可能会存在一定的误差。 选取过隧道中心(xc，yc)的水平轴，截取该水平轴上下各25 cm 的点云根据式(18)进行二次曲线拟合。

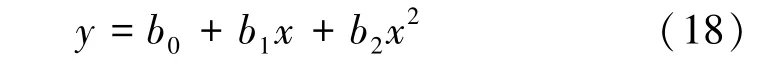
以左侧为例，截取的点云个数为N，设置权阵P 初始值为单位阵，参数阵X 初始值为零矩阵参与计算，根据间接平差公式并采用第2.2 节所述的选权迭代法解算得到二次拟合曲线的最优解()，进而可获得过隧道中心的水平轴与隧道左侧的交点((--)/2，yc)。 同样，水平轴与隧道右侧的交点也可获得，进而可求得隧道断面的水平直径。

3 实例分析

3.1 工程概况

以武汉市地铁某盾构隧道为例，该段隧道长1.630 km，盾构管片采用混凝土浇筑，设计内径5 400 mm，点云数据通过车载移动测量系统获取。 将截尾最小二乘法、选权迭代法和二次曲线拟合法通过编程实现，根据里程信息提取指定位置处的隧道断面点云后，将其输入处理程序中解算得到椭圆拟合参数与二次曲线拟合参数。 为提高程序运行效率，设置迭代次数为4(一般迭代3 次即可获得高精度解)。 图8 中蓝色部分为断面点云数据，红色为拟合椭圆。 图9 红色为断面两侧拟合的二次曲线，蓝色线为断面水平直径。 图10 为根据项目实际需求自定义的断面拟合成果，包含了断面所在位置的盾构环号、拟合椭圆的长短半轴、椭圆度、偏转角和水平直径等信息。

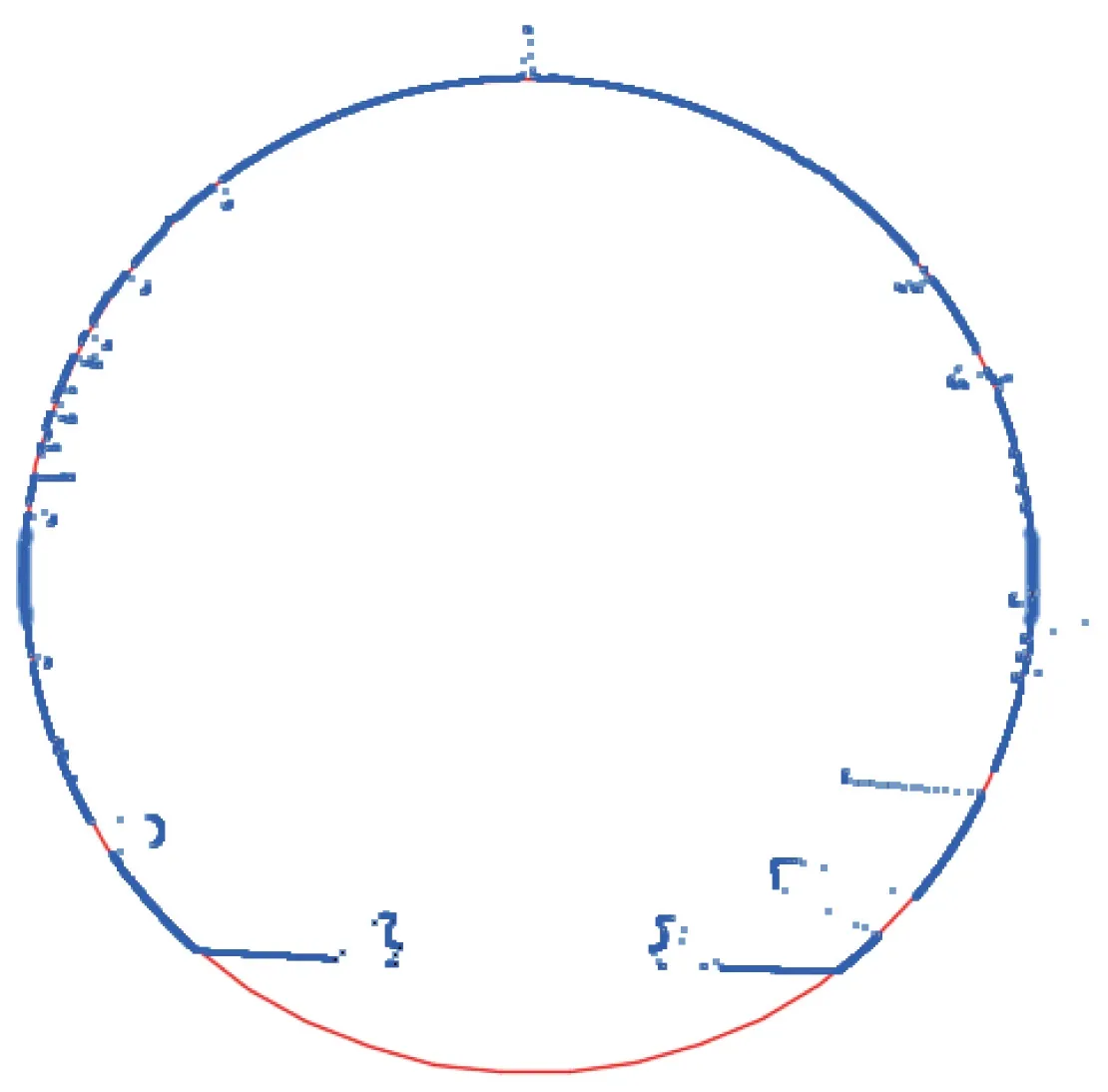
图8 隧道断面拟合椭圆

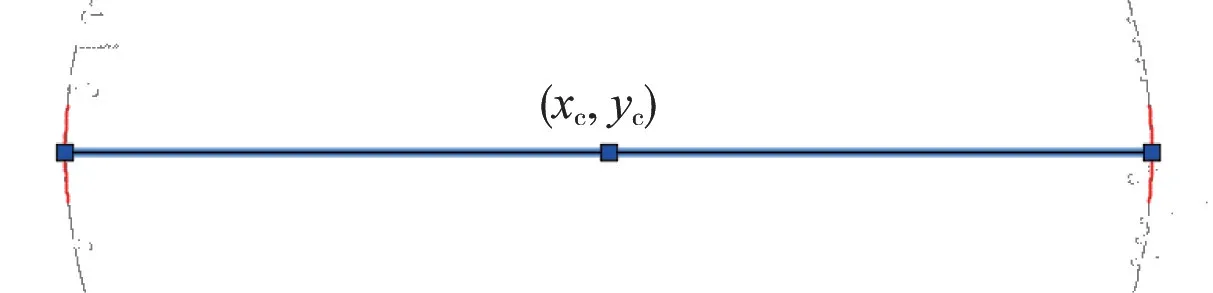
图9 二次拟合曲线与水平直径

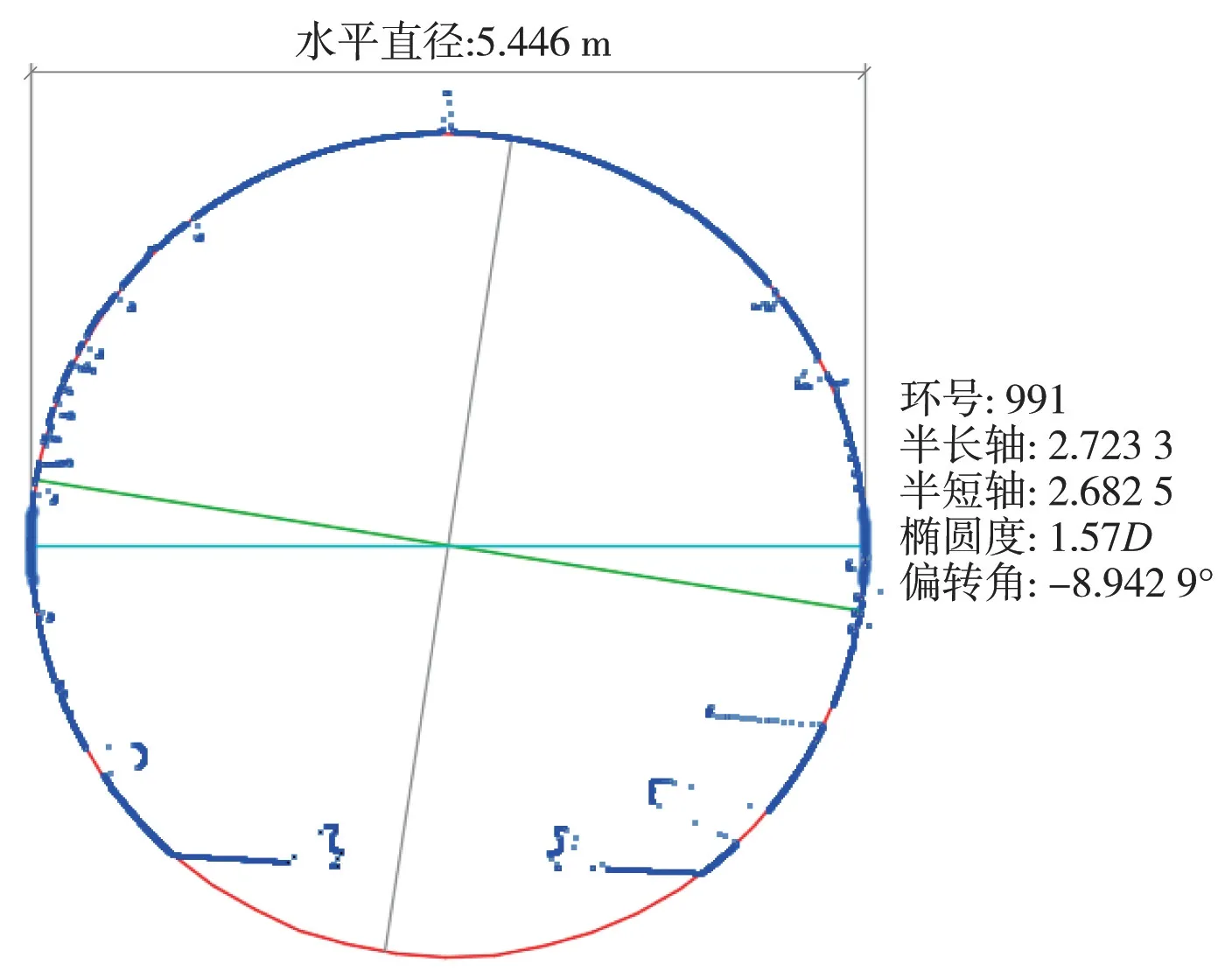
图10 隧道断面拟合成果

3.2 精度验证

采用回归统计中的调整后的R2这一指标进行椭圆拟合精度验证。

R 代表相关系数，是衡量两个变量之间相关性的一个相对指标，其计算公式为

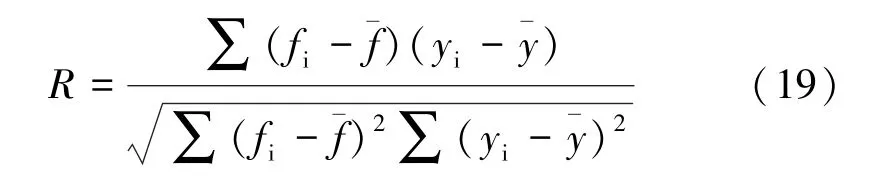
其中，yi代表点云中每个点(xi，yi)的Y 坐标值，¯y代表所有点云Y 坐标值的平均数。 fi代表拟合椭圆在相同位置xi处的Y 坐标值，¯f 代表所有fi的平均数。

R2称为判定系数，是度量拟合优度的统计量，代表了实际观测值与回归模型之间的离差平方和与总离差平方和之比，在数值上为相关系数R 的平方，取值范围为0～1。 理论上，在得到椭圆拟合参数后，对实际观测值与拟合值进行统计分析时，R2代表了椭圆方程的精度，即椭圆方程与断面点云的拟合程度。 当R2的数值越高时，椭圆方程的拟合程度越好，精度越高。

然而在实际应用中，随着自变量个数的增加，R2也会逐渐增加，单纯从数值上观察可能会造成回归模型拟合效果很好的假象[14]。 为此，采用(调整后的R2)来评价椭圆拟合的精度，当其为0.7 时，可认为模型选择正确且拟合程度较好。

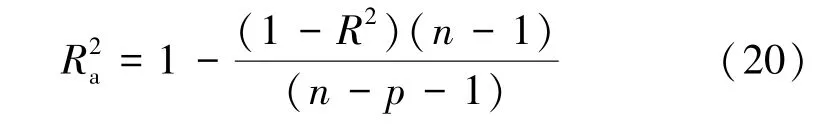
其中，n 为样本总数，p 为自变量个数(此处为5 个椭圆参数)。

随机提取8 个隧道断面进行椭圆拟合后，分别按照式(20)计算，统计结果如表1 所示。

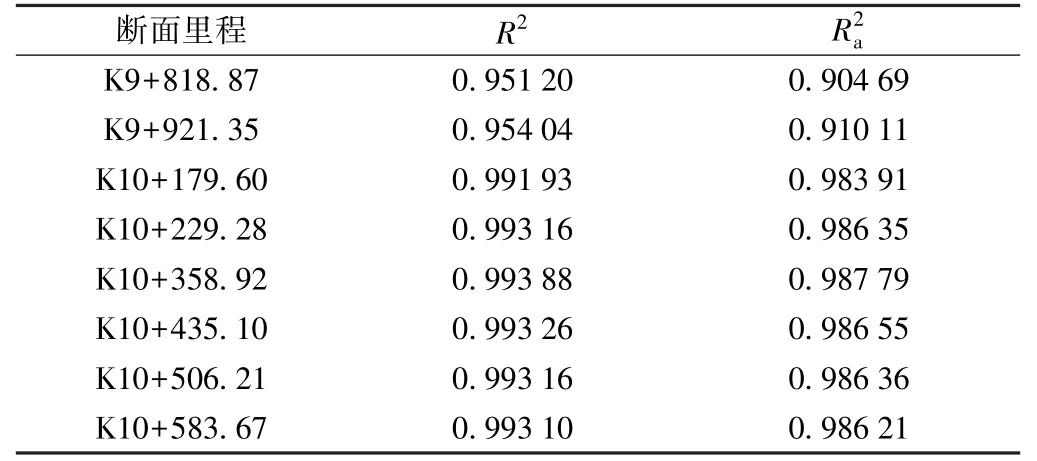
表1 椭圆拟合精度验证统计

水平直径拟合值与设计值对比统计如表2 所示，由表2 可知，随机选取的各断面中，采用二次曲线拟合方法计算的隧道水平直径与设计直径D 的差值ΔD 均小于1.2 cm，其相对变形(ΔD/D)均满足GB 50157—2013《地铁设计规范》中3‰～4‰的规定。 通过与水平直径的设计值对比，直观地反映出地铁隧道断面的变形情况，为后期的养护维修提供了数据支持。

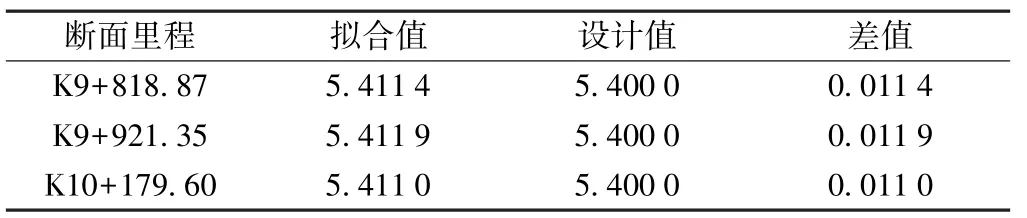
表2 水平直径拟合值与设计值对比统计 m

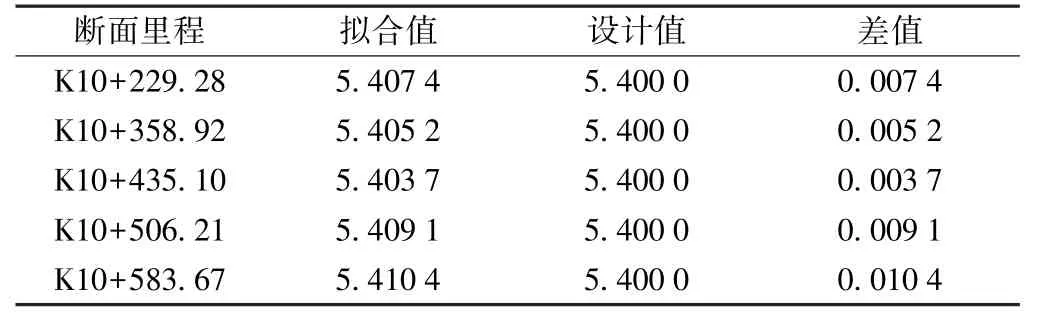
续表2

4 结论

利用车载移动测量系统采集的盾构隧道点云数据进行断面收敛检测分析时，采用截尾最小二乘和选权迭代相结合的方法进行椭圆拟合，不仅可以有效抵抗点云数据中噪声和粗差的影响，获得拟合程度较高的椭圆参数，进而计算得到较高精度的椭圆度、水平直径以及偏转角等检测值，还可以较快获取拟合初值，减少迭代时间，提升数据处理效率，在工程项目应用中具有良好的可靠性与推广应用价值。