CPⅢ自由测站三角高程法测量误差研究

陈 倜

(中国铁路设计集团有限公司，天津 300251)

CPⅢ控制网为铁路建设与安全运营提供坐标基准，是一种三维坐标控制网，分为平面控制网和高程控制网。CPⅢ高程控制网测量最早采用的是德国中视法[1]，这种方法能满足CPⅢ高程控制网测量的要求，但是不能适应我国高程测量体系[2]。 为此，许多学者进行了相关研究，在学习德国中视法的基础上提出了适合我国高程规范体系的矩形法，该方法可靠性高，探测粗差能力强[3]；李建平为提高矩形法外业作业效率，提出了Z 形法，效率和精度较矩形法都有所提高[4]；刘定威提出了新矩形法、单程矩形法和双程矩形法，其中新矩形法和单程矩形法效率最高，双程矩形法能严密求解每千米偶然中误差[5]。 上述方法都是通过电子水准仪直接测量两个 CPⅢ点之间的高差来构建CPⅢ高程网。

然而，最高效的方法是直接利用CPⅢ平面控制网测量数据中的斜距和竖直角计算CPⅢ点间的高差，进而构建CPⅢ高程控制网。 付建斌基于这种思想，提出了基于自由测站三角高程的CP Ⅲ控制网测量方法(简称“三角高程法”)[6]；刘成龙提出了三角高程法的完整平差方法和相应的数学模型[7]。 研究表明，绝大多数情况下，该方法能满足CPⅢ高程控制网的精度要求，但是也存在少量超出精度限差要求的情况。 李建章进一步提出了参数法平差模型，该方法在一定程度上提高了成果精度，降低了成果超限率[8]；王子轩改进了三角高程法的构网方式，并应用于地铁 CPⅢ高程网建网中，取得了较好的效果，但是该方法没有充分利用三角高程测量的角度和距离值[9]；高山对这种方法进行改进，采用单测距单向观测的方法进行高铁路基冻涨监测，在一定条件下能达到二等水准的精度[10]；郝旦等认为三角高程法存在一定的问题，部分成果与精密水准成果较差甚至达到3 cm[12]。 综上所述，三角高程法与水准仪测量方法相比，省去了 CPⅢ高程控制网精密水准测量工作，提高了效率，节省了外业工作成本，在大部分情况下能满足高速铁路CPⅢ高程控制网建设的要求， 但是也难免存在一些测量成果精度不满足限差要求的情况，这也是三角高程法难以在工程实践中广泛应用的主要原因。

在其他一些精密工程测量领域中，研究者通过采取一些特定的方法来改善三角高程测量精度:丘志宇通过多测回、多时段观测、选择垂直大气折光变化对称的时间观测等方法来提高三角高程测量精度[13]；孔宁等通过使用两台高精度自动照准全站仪进行同时段对向观测，测量成果能达到二等水准的精度[14-15]；吴迪军使用同时段对向观测法，在特制观测标志的配合下，实现长距离跨海高程传递，并且满足二等水准测量限差[16]。 由于铁路CPⅢ控制网每隔60 m 布设一对CPⅢ点，数量较多；并且CPⅢ控制点采用特定的预埋装置，无法采用多时段观测、对称折光时间段观测、同时段对向观测等方法来提高测量精度。

为了系统研究三角高程法误差产生的原因，首先对其可能的误差来源进行分析，然后结合山东省某高速铁路CPⅢ建网项目，定量比较分析三角高程法测量得到的高差与精密水准法得到的CPⅢ点间高程差，最后根据多年的CPⅢ测量经验，给出一些建议。

1 CPⅢ三角高程法误差分析

三角高程法CPⅢ高程控制网是以CPⅢ平面控制网测量数据中的斜距和竖直角为基础构建的。 每1 个测站通过高精度智能全站仪测得12 个(联测CPII 时为13 个)CPⅢ控制点的斜距和竖直角，1 个测站测量完成后，把全站仪向前移动2 对CPⅢ控制点(约为120 m)，最后形成边角测量网，如图1 所示，图中直线表示设站点到CP Ⅲ点的一组斜距和竖直角的测量值。

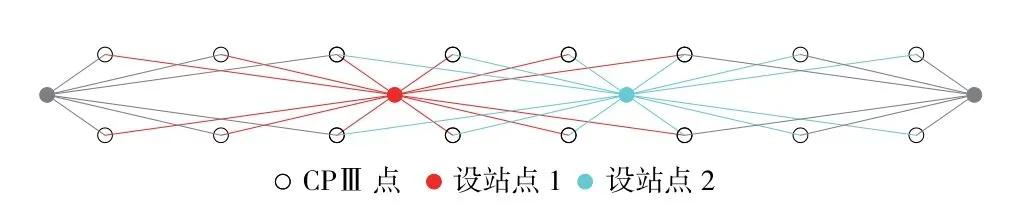
图1 CPⅢ三角高程法测量示意

设站点与每个CPⅢ控制点棱镜中心之间的高差h 的理论计算公式为

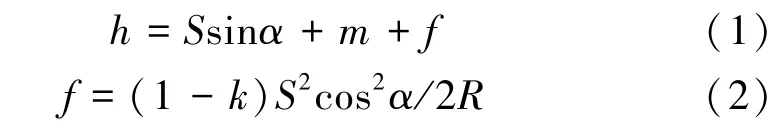
式(1)和式(2)中，S 为设站点到某个CPⅢ控制点棱镜中心的斜距，m 为该测站仪器高，f 为大气折光影响值，α 为测量方向的垂直角，k 为测量方向的平均大气折光系数，R 为地球平均曲率半径。

将同一测站到两个相邻CPⅢ控制点p 和q 间的高差进行差分，得到p、q 棱镜中心之间的高差表达式

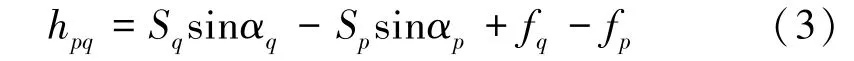
式(3)中，难以精确计算的是大气折光影响值fp和fq。 根据规范要求[1]，S≤180 m，k 值受温度、气压等因素影响，难以得到准确值，根据经验取0.13 ～0.14[9，17]，地球平均曲率半径为6 371 km，故大气折光影响值f 为亚毫米级，对高差影响很小，而且fp和fq能部分抵消，在实际应用中，该项值可以忽略不计，则式(3)可以简化为

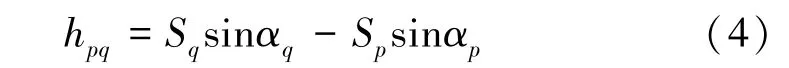
式(4)中，引起误差的为斜距S 和竖直角α，而斜距S 误差引起的高差误差也可以忽略不计，故引起高差误差的是竖直角α 测量误差。 竖直角α 测量误差分为两部分:一类是随机误差，另一类是系统误差。 目前，CPⅢ测量使用的仪器精度大多为0.5″级，一般情况下，随机测量误差影响较小[18]，为了简化问题，在此不予讨论。 因此，对竖直角测量误差影响较大的可能是仪器系统性误差，这种系统性误差产生于仪器长途运输以及仪器老化过程中。 系统性误差往往导致测量值呈现出一定的趋势性，在此对这种趋势进行分析。假定竖直角αi的测量值为，仪器系统性误差为αs，则竖直角测量值可表示为

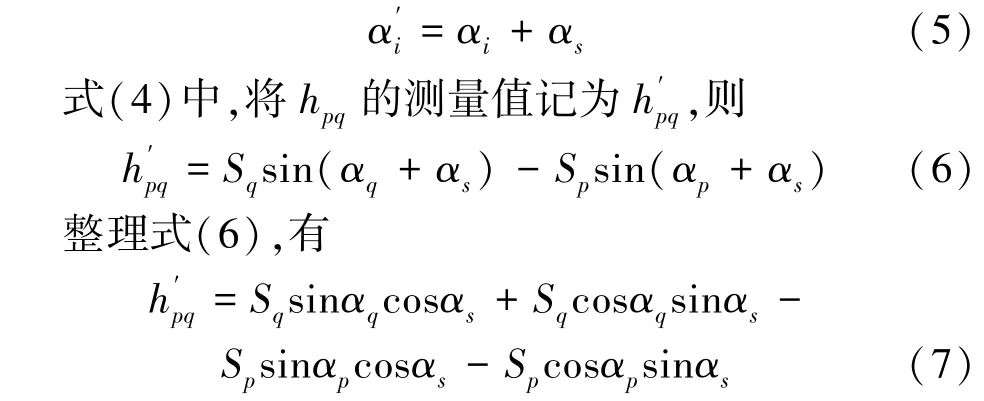
式(7)中，αs是一个秒级的微小量，故cosαs约等于1，sinαs约等于αs，式(7)可以做如下简化

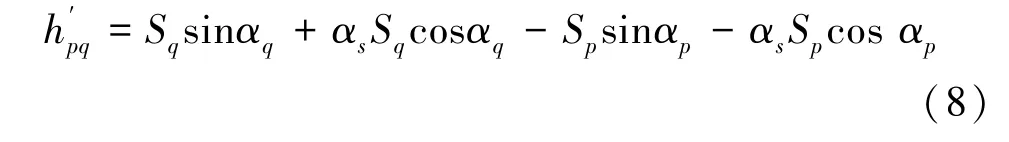
式(8)中，Sqcosαq是设站点到棱镜q 的水平距离，记为Lq，Spcosαp是设站点到棱镜p 的水平距离，记为Lp，把式(4)代入式(8)，有

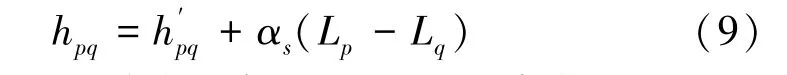
显然，hpq测量精度受仪器系统性竖直角测量误差αs和设站点到p 和q 两个棱镜中心的水平距离差影响，系统误差稳定的情况下，距离差越大，测量误差越大。

2 实例分析

2.1 精密水准法CPⅢ高程测量

以山东省某高速铁路CPⅢ项目中DK100+994.74～DK105+343.44 段建网数据为例进行说明。 先用精密水准法对该段落CPⅢ高程控制网进行测量，其水准线路测量行进方式如图2 所示，每个四边形环由四组高差构成，每2 km 左右联测一处线上加密水准点。

图2 CPⅢ水准测量示意(单位：m)

CPⅢ精密水准网构网方式如图3 所示，CPⅢ高程网测量精度如表1 所示。

图3 CPⅢ水准闭合环示意

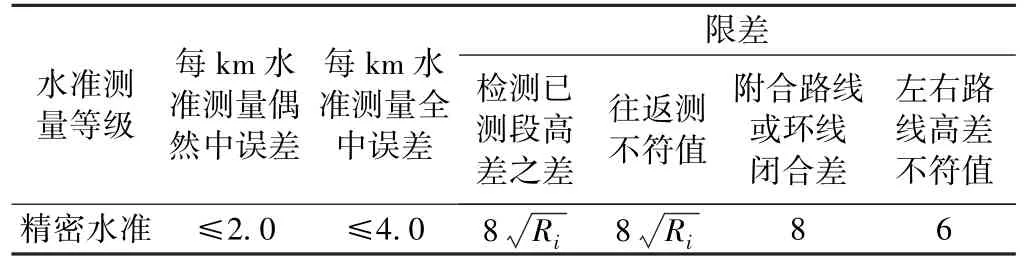
表1 CPⅢ精密水准测量精度要求 mm

所有测量结果均满足精度要求，使用TSDI_HRSADJ 平差软件严密平差后得到的所有CPⅢ控制点的高程。

2.2 三角高程法CPⅢ高差测量

为了分析三角高程法的测量精度，用CPⅢ平面网中的斜距和竖直角计算CPⅢ点与设站点间高差，然后再对这些高差进行差分，得到CPⅢ点的间接高差。 三角高程法测量路线如图1，每1 个测站完成测量之后，向前平推2 对CPⅢ控制点，再进行下一站测量。 三角高程法测量精度如表2 所示。

表2 CPⅢ三角高程法精度要求

通过不同测站相邻控制点间的间接高差构成高程网，如图4 所示。

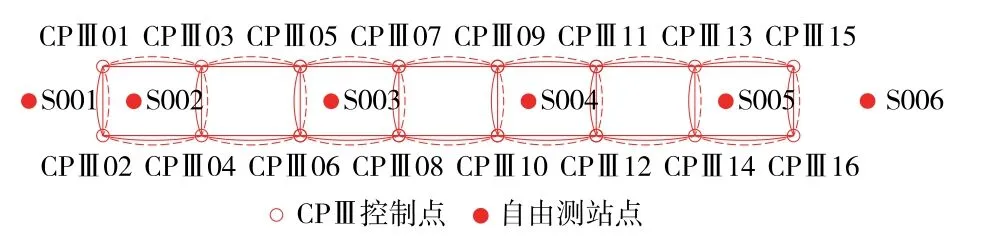
图4 CPⅢ三角高程网示意

由于每1 个CPⅢ控制点分别被3 个不同测站观测，故任意相邻控制点之间都有2 ～3 组高差观测值(存在多余观测值)，这些多余观测可以互为检验条件，是判断数据质量好坏的重要依据之一。

2.3 三角高程法误差定量分析

为了分析三角高程法CPⅢ高差测量误差，把精密水准法平差后的CPⅢ高程成果近似当作真值，计算三角高程法CPⅢ点对间的高差与高程差的差值，以此近似三角高程法高差测量误差，经过分析发现，三角高程法高差测量误差与全站仪设站点到两个CPⅢ点的距离差显著相关，如图5 所示。

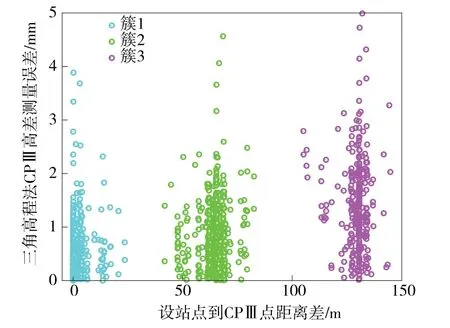
图5 三角高程法高差测量误差与距离较差关系散点

从图5 中可以看出，高差测量误差和距离较差散点图呈现出一定的聚集性特征，通过聚类分析，得到3 种颜色所示的3 个簇。 从簇1 到簇3， CPⅢ高差测量误差平均值越来越大，离散程度也越来越高，与之对应的是设站点与相应CPⅢ点间的距离差也越来越大。

进一步分析发现，3 个簇分别对应着3 种不同的CPⅢ高差类型:簇1 对应的设站点到两个CPⅢ点间的距离差离散分布在0 附近，平均值为2.3 m，如图6(a)中设站点与C5和C7、C7和C8、C9和C10、C11和C12这几对点的情形，这种类型的距离差定义为Ⅰ级；簇2 对应的设站点到两个CPⅢ点间的距离差离散分布在65 m 附近，平均值为64.6 m，如图6(b)中设站点与C7和C9、C9和C11这两对点的情形，这种类型的距离差定义为Ⅱ级；簇3 对应的设站点到两个CPⅢ点间的距离差离散分布在130 m 附近，平均值为129.5 m，如图6(c)中设站点与C7和C11这对点的情形，这种类型的距离差定义为Ⅲ级。 当设站点到两个CPⅢ点距离差为Ⅰ级时，三角高程法高差测量平均误差为0.545 mm；当设站点到两个CPⅢ点距离差为Ⅱ级时，三角高程法高差测量平均误差为0.813 mm；当设站点到两个CPⅢ点距离差为Ⅲ级时，三角高程法高差测量平均误差为1.403 mm，平均误差与距离较差平均值的关系如图7 所示。

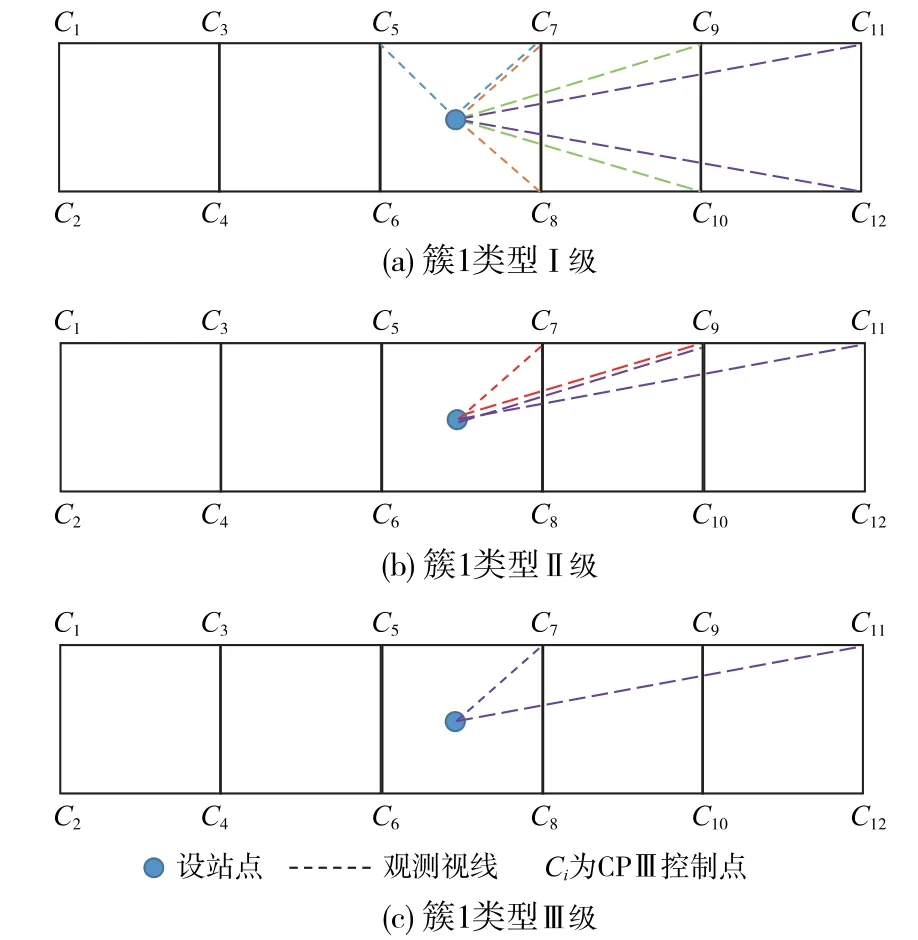
图6 设站点到CPⅢ点间距离差示意

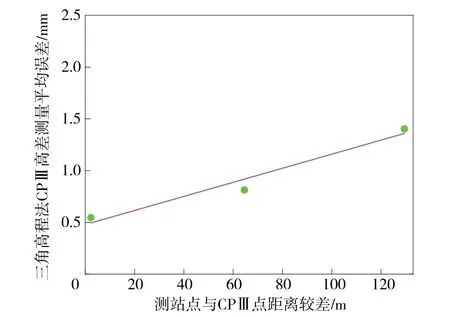
图7 三角高程法高差测量平均误差与距离较差平均值关系

从图7 中看出，高差测量误差平均值随设站点到CPⅢ点距离差的平均值增大而增大，二者相关性系数无限接近于1；同时从图中拟合的直线来看，三个等级的高差测量误差平均值与距离差平均值近似线性相关，侧面验证了式(9)表达的函数关系。 根据拟合的线性函数关系，对三角高程法测量的高差进行修正，分别用修正前后的结果与水准法观测成果进行比较，并分别采用相对平方误差(RSE)、正态均方误差(NMSE)、均方根误差(RMSE)和绝对误差(MAE)进行全面定量评估，各精度指标的计算结果列于表3。 由表3 可以看到，对三角高程法高差观测值进行修正后，其各项精度指标均优于修正前的各项指标，说明利用这种线性函数关系能优化三角高程高差观测成果的精度。

表3 高差测量值修正前后精度评估

3 结论

首先对CPⅢ三角高程法测量误差进行了分析，发现该方法测量误差受竖直角测角误差影响较大；进一步分析系统性测角误差对高差观测值的影响，发现在一定系统性测角误差条件下，高差测量误差与设站点到两个CPⅢ点间距离差近似呈现线性相关关系，利用这种线性函数关系修正三角高程法高差观测值，实验结果表明，修正后的高差观测值精度优于修正前的高差观测值，为下一步研究如何在实际工程应用中有效降低系统性竖直角测角误差的影响提供了依据。