基于改进蚁群算法的智能船舶路径规划*

龚铭凡 徐海祥 冯 辉 薛学华

(高性能船舶技术教育部重点实验室1) 武汉 430063) (武汉理工大学交通学院2) 武汉 430063)

0 引 言

智能船舶由智能机舱、智能船体、智能航行、智能能效管理、智能货物管理，以及智能集成平台这六个模块组成[1].其中路径规划是智能航行的重要组成部分，其任务为依照单个或多个优化准则(如距离最优、时间最短、安全性最高等)，找到从初始节点至目标节点避开障碍物的最优或较优路径[2-3].目前，路径规划方法主要有以下三类：传统路径规划方法、基于生物智能和基于强化学习的路径规划方法.第一类路径规划方法有A*算法[4]，Djikstra算法[5]，人工势场法[6]等.A*算法在Djikstra基础上加入启发式估计，提升了搜索效率，然而面对复杂环境，其效率仍然很低.文献[7]针对复杂环境A*算法计算时间长，提出时间效率A*算法.文献[8]通过修改斥力函数，使人工势场法避免陷入局部最小值而无法跳出，其主要应用场景为目标不可达情况.第二类基于生物智能的方法有粒子群算法[9]、蚁群算法[10]、遗传算法[11]、神经网络[12]等.这些群智能算法全局寻优好，不需要建立复杂的环境模型，但参数较多且不确定、收敛速度慢、算法复杂度较高.文献[13]将粒子群算法与遗传算法相融合，用于解决自主无人机在三维环境的复杂问题.文献[14]针对传统蚁群算法易陷入局部最优的问题，在路径搜索过程间产生蚂蚁，开辟新路径，增加跳出局部最小值的可能.第三类基于强化学习的方法有Q-leaning算法[15]，Sarsa算法[16]等.与之前的算法相比，强化学习具有学习能力强、复杂未知环境适应度好等优点，但是目前的强化学习中试错学习、状态泛化，需消耗大量资源[17].综上所述，每种算法都有各自的优点与局限，因此，混合算法为路径规划提供了一个新的思路，取长补短，从而有效解决实际工程问题.

文中提出的基于势场启发式信息的改进蚁群算法，在寻径过程中，引入船舶受到引力、斥力与其到目标点的间距相结合构建启发式信息，为算法进行全局路径规划提供搜索策略，防止其进入局部最优.改进传统信息素更新，加入最差蚁群对整个蚁群的负面作用，加快收敛，并对信息素系数进行自适应调节，提升全局搜寻能力.仿真实验分别比较了传统算法与本文算法在两种不同环境下的搜索性能，并对算法中的重要参数进行了敏感性分析.

1 基本蚁群算法

1.1 栅格法环境建模

将障碍物按照船舶的半径进行适当膨胀，再将未填充满的栅格补充完整(见图1)，以确保船舶进行无碰撞运动.蚁群算法对栅格的访问以一个栅格中心位置为准，不可在栅格的端点或边界处.栅格标识常见方法有直角坐标法和序号法，且二者可互相转换.采用序号法，对栅格地图从上至下、从左至右进行标识，栅格序号集为S={1,2,…,E}.E为右下栅格，对于N1×N2的栅格空间，E=N1×N2.

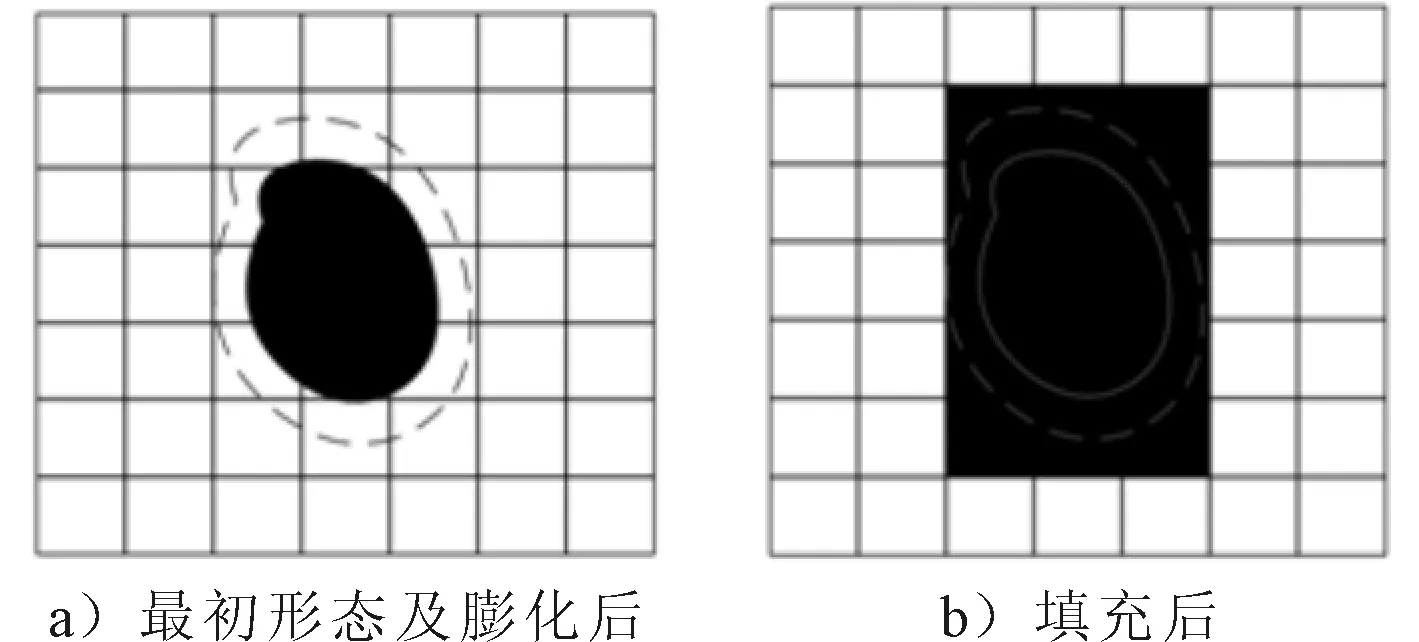
图1 障碍物栅格化

1.2 蚁群算法的基本原理

算法中最为重要的两个步骤为转移概率选择以及更新信息素的方式.转移概率选择，即一只蚂蚁在当下节点前往下一节点是按照一定的几率去选取.蚁群算法通过轮盘赌的形式选取下一位置，其状态转移概率为

(1)

式中：am={1,2,…,n}-Bm为蚂蚁可选择的节点集合；Bm为禁忌表(蚂蚁m走过的点)；α为信息素启发因子，表示之后的蚂蚁寻径时受信息素影响程度；β为期望启发因子，表示蚂蚁受启发信息影响大小；ηij为启发函数，表示当前蚂蚁领域j到目标E的间距启发信息,ηij(k)=1/djE.

启发信息以及信息素浓度大小是蚂蚁选取路径的关键依据，由于信息素浓度会跟随时间增加而慢慢消失，所以算法会更新局部及全局信息素，为

τij(k+1)=(1-λ)τij(k)+τ0

(3)

τij(k+1)=(1-ρ)τij(k)+Δτij(k)

(4)

其中：

(5)

式中：1-λ为局部信息素残留系数；ρ为全局信息素挥发系数；τij(k)为第k次迭代时节点i、j间信息素；τ0为初始信息素浓度，是一个小的常量；Δτij为蚁群一次迭代后信息素增量；Q为信息素强度；Lm为蚂蚁m在本次循环中的路径长短.

由式(6)可得，节点i，j之间留下的信息素强度和路径优化程度息息相关，路径越短，留下信息素浓度越高，而蚁群将跟随浓度较高的路径.

2 基于势场启发式信息的改进蚁群算法

2.1 改进启发信息

借鉴人工势场法的思想，障碍物在其四周的一定范围内存在斥力场，而目标节点对船舶形成一个引力场，即船舶在整个环境中所受的合力为目标节点的引力与障碍物的斥力相加.

将以上势场信息与距离信息相结合从而改进启发信息，使蚂蚁向合力方向寻径，其中势场合力启发信息为

ηs(k)=cFtol·cos θ

(7)

式中：c为正常数；θ为势场合力Ftol与蚂蚁可选路径间的夹角.在此条件下，蚂蚁从当前位置到下一节点位置的选择会趋向于夹角θ较小的方向.该部分启发信息引入了环境势场信息，可更有效地使船舶避免与障碍物的碰撞.

综合距离启发信息式(2)得：

(8)

由于人工势场本身会存在引力与斥力相抵，即合力为0的情况，此时会陷入局部最小值，若仅采用势场力作为启发信息，就会陷入局部最小值而无法逃脱.而综合蚁群算法本身的启发信息，即使势场合力为零，仍拥有距离信息作为启发信息，引导船舶跳出局部最优，继续寻找最优路径.

2.2 改进信息素更新

修改全局信息素更新机制，加入最差蚁群的影响，对残留信息素与当前信息素加权，其更新规则为

τij(k+1)=g(1-ρ)τij(k)+(1-g)Δτij(k)

(9)

(10)

(11)

(12)

式中：ρmin为挥发系数阈值.由式(12)可见，挥发系数会越来越小直至到达最小值.

2.3 算法步骤

改进算法流程图见图2.

图2 改进算法流程图

3 仿真结果与分析

蚁群算法中的参数的最优选取目前还没有严谨的理论支撑，主要取决于统计数据以及经验.但算法中的重要参数，如启发式因子、蚁群数量等，都会对路径规划的结果优劣产生重要影响，因此对参数进行敏感性分析具有重要意义.

文中设置两个路径规划环境分别为：20×20个栅格，较少障碍物；30×30个栅格，较多障碍物，见图3.

图3 算法运行环境

3.1 启发式因子的影响

信息素启发式因子α的大小表示遗留信息素对蚁群寻径影响大小，而期望启发式因子β的高低体现启发函数于寻径中重要程度.图4为信息素启发因子对应的最优距离.由图4可知，不论是简单、复杂环境，还是算法改进前后，曲线整体大致都是随着α的增加而下降直至稳定.除此以外，改进算法比原算法更容易寻得最优路径且在长度上占优.结合改进后的两种环境曲线变化，选取α=0.8，路径相对最短，此时观察期望启发式因子的变化.

图4 信息素启发式因子α对应最优距离

图5为期望启发因子对路径长度的影响，图中的曲线趋势均为递减，即β越大，最佳路径长度越短.由图5可知，相对于基本蚁群算法，本文提出的改进势场蚁群算法寻得路径更短、更为稳定，并且环境越复杂，路径长度差异越大.通过简单、复杂环境曲线，选择β=4，使两者路径长度均最优.因此，最佳的启发式因子组合为α=0.8，β=4.

图5 期望启发式因子β对应最优距离

3.2 蚂蚁数量的影响

蚂蚁数量对算法得到的最优路径影响见图6.相较于原算法曲线的大波动，改进蚁群算法得到的曲线更为平滑.在简单环境中，当M=50时，本文算法得到最优解，且蚁群数量增加，路径长度不变；复杂环境下，蚂蚁数量为70时，路径最短，且随着数量加大，所得解在其上下微小波动.考虑到时间复杂度及迭代收敛速度，选取蚁群数量为60最为适宜.

图6 蚁群数量M对应最优距离

3.3 最优参数下路径规划仿真分析

运用传统蚁群算法和改进蚁群算法在仿真平台进行实验.参数设置：蚂蚁数量M=60，迭代次数K=60，初始信息素挥发系数ρ=0.4，启发式因子α=0.8，β=4.图7为船舶在两种不同环境下，通过改进算法得到了全局最优路径.

图7 改进算法路径规划

两种算法对比结果见表1.由表1可知，在两种算法均各自收敛至最优后，时间上，本文算法为0.9,和9.8 s，与基本蚁群算法的3.5和16.6 s相比有显著提升；路径上，在简单环境下路径相差不大，但在复杂环境情况下差距明显，本文算法路径长度为45.9 m，较基本蚁群算法减少了7 m左右.因此，本文算法在路径长度及时间成本上更优.

表1 两种算法对比结果

两种环境下的迭代收敛曲线见图8.由图8可知，两种环境下，原算法均收敛较为缓慢且一直在振荡，而本文算法均循环12次左右收敛至最优且较为稳定.

图8 两种环境下的迭代收敛曲线

由于蚁群算法规划的节点均为栅格中心，使得计算出拥有较多转折点及一些不必要的路径，因此，对算法生成的曲线进行平滑处理.若路径连续三个点连接不过障碍物，则将中间点剔除；反之，路径保持不变.以此类推，保留必需点，剔除多余点，获得路径长度分别为28，45 m，由此可得，缩减后的路径更为平滑且长度更短，见图9中虚线部分.

图9 路径缩减之后的路径规划

4 结 束 语

文中提出了一种改进蚁群算法适用于全局静态的路径规划.利用势场合力作为启发函数的一部分，让船舶有效规避障碍物且不断靠近目标节点，结合距离启发信息，使船舶更快寻得最近路线.针对原算法复杂度高、收敛速度较慢且消耗时间长等问题，加入最差路径蚁群影响，修改全局信息素更新机制，增加收敛速度，降低算法时间.针对基本蚁群算法及改进蚁群算法中重要的参数采用单因素法，分析其对路径规划的路程及时间的影响.在最优参数的基础上，将两者进行分析比较.仿真结果证实了改进后算法的有效性及可行性.最后采用路径缩减，将获取的路径曲线进行优化处理.本文的仿真环境为全局静态，后续将结合未知环境及动态障碍物进行局部路径规划研究.