船体结构波浪中逐次崩溃特性实验研究*

吴 彤 裴志勇 吴卫国

(武汉理工大学绿色智能江海直达船舶与邮轮游艇研究中心 武汉 430063)

0 引 言

作用于船体结构的外载荷和结构极限承载能力是确保结构安全可靠最重要的两个方面.传统上一般把外力和结构耐力分开来考虑，忽略相互作用进行结构安全性评价.随着计算技术的发展和计算效率的提高，研究者们开始考虑流体与结构的耦合作用，进行载荷(结构响应一体化计算分析.Iijima等[1]基于势流理论，运用三维时域准静态分析方法，对一艘集装箱船进行了载荷计算和结构响应分析.Yao等[2]建立载荷(结构响应一体化计算分析系统，基于势流理论计算作用于船体的随时间变化的载荷，将载荷施加到结构模型上，进行结构非线性响应分析，得到特定海况下船体结构的极限强度.Xu等[3]结合水弹性理论与非线性有限元法，对一艘散货船在极限海况下的动力崩溃行为进行了研究，对船体梁在超越概率为10-3的极限海况下的船体崩溃过程进行了分析.裴志勇等[4]将三维奇异点分布法计算流体载荷与理想结构单元法计算船体结构响应结合起来，对一艘82 000 t散货船在遭遇极限海况时随时间分布载荷特性和结构逐次崩溃特性进行了计算分析，明确船体结构的崩溃过程和极限强度.

由于作用于船体载荷和结构非线性响应分析的复杂性，其数值计算结果的精度一直困扰着研究者们.国际船舶结构大会(ISSC)曾多次就同一船体模型的极限强度进行对比计算，各国研究者用不同数值方法得出的结果分散性是相当大的.实验方法是揭示事物本质的最根本最有效的手段，相对于数值计算，模型实验能够更为准确、全面的呈现船体结构在波浪中所受载荷和结构崩溃发生过程.Xu等[5]采用中部塑性铰在船舯部连接两端1/2刚性船体，在波浪水池中进行了单个规则波下的极限强度实验.通过分析中部塑性铰的受力状态，确定逐次崩溃过程中船舯剖面弯矩与船体变形的关系，进而可获得船体结构的极限强度.Iijima等[6]考虑波浪载荷的累加效应，进行了连续波浪作用下船体结构累积塑性破坏实验，对极限强度后船体结构承载能力的降低进行了分析.Liu等[7]将两段刚体模型通过塑性铰连接，通过改变波长的方式来模拟船体遭受不同的极端波浪，对船舶的动力承载特性进行了研究.上述实验都是将两刚体模型通过塑性铰连接来进行实验，可得到作用于船体的载荷，无法获得结构崩溃特性.张水林[8]进行了三舱段模型波浪中的崩溃实验，由于造波能力有限，为使船体结构发生崩溃，实验段采用0.5 mm不锈钢板，加工时产生了非常大的初始变形，使得实际模型的崩溃特性有所不同.

为了探究船体结构在波浪中的崩溃特性，揭示其崩溃机理，本文设计并制作了三舱段铝合金船模，在波浪水池中进行船体结构崩溃实验.在模型底部典型位置布设压力传感器以测量实验过程中该处的压力变化状况，在中间舱前后舱壁位置分别布设角度传感器测量中部舱段的弯曲变形情况，在船中剖面布置系列应变测点获取不同时刻船体结构应力分布状况.实验时，首先将船模静置于造波水池中，在首尾端施加固定质量，在中部实验段形成静水弯矩；随后不断增加波高，从而作用于船模实验段段的载荷不断增大，直至船体结构发生崩溃为止.通过对船体结构崩溃过程中的载荷、结构应力分布及变形特性进行分析，揭示船体结构波浪中逐次崩溃特性.

1 实验流程

为探究船体结构波浪中逐次崩溃特性，设计具有典型船体结构特征的三舱段铝合金船模，在波浪水池中进行崩溃实验，实验步骤见图1.

2 实验方案

2.1 实验模型

为获得船模结构波浪中的崩溃特性，其所受载荷须大于结构承载能力，这是实验模型结构设计原则.考虑典型船体结构特征，设计三舱段船体结构模型，中间舱段为实验段，艏艉舱段可视为加载段.模型材料采用屈服强度较低的铝合金，艏艉加载舱段结构较强，实验时不发生崩溃；中间实验舱段结构设计的稍弱，在静水载荷和波浪载荷联合作用下发生崩溃.

实验船模各舱段长2.25 m，模型总长6.75 m、型宽1.0 m、型深0.3 m.艏艉加载舱段的端部甲板各有长0.3 m、宽0.5 m的开口，以便在艏艉端放固定压铁，形成静水弯矩.艏艉舱段甲板和船底均布3道加强筋，纵骨尺寸为20 mm×3 mm，横向强框架尺寸为50 mm×3 mm，板厚3 mm；中间舱段甲板大开口，甲板条宽0.3 m，船底均布3道加强筋，纵骨尺寸为20 mm×1.5 mm，横向强框架尺寸为30 mm×1.5 mm，板厚1.5 mm；实验模型结构图见图2.

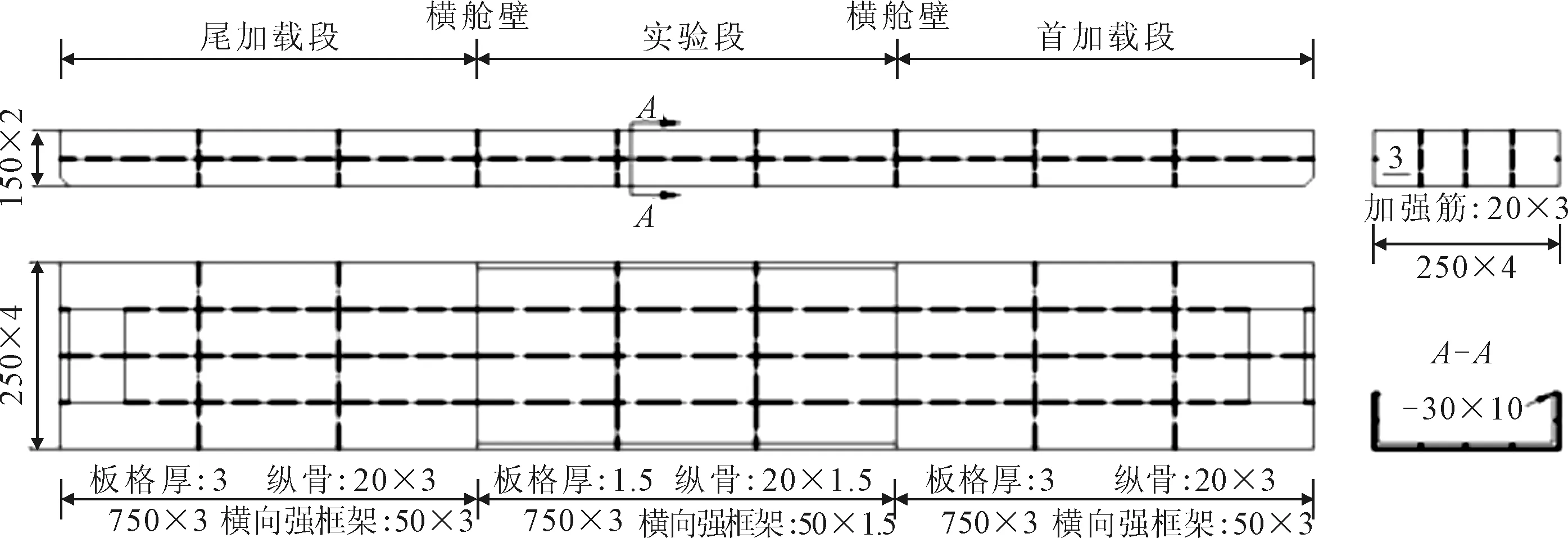
图2 实验模型结构图

考虑造波水池实际的造波能力，为保证模型结构承载能力要小于所受外力发生崩溃，实验模型采用强度相对较弱的3105-O态铝合金，根据材料试样拉伸实验结果，其屈服强度取为40 MPa，相关力学性能指标见表1.

表1 实验模型铝合金材料力学性能

2.2 实验内容

为获得船体结构波浪中的崩溃特性，实验中要测量波浪的状态、船体结构变形状况以及典型剖面应力分布状况等.在实验模型底部布置系列水压力传感器以获得波浪的状态，以便计算波浪载荷；在模型实验段前后横舱壁位置布设角度传感器，测量中部舱段的弯曲变形情况，用来计算实验模型的转角及曲率；船中剖面布置系列应变测点，测量结构应力分布状态.各测试设备在模型实验段布置状况示意图见图3.

图3 测试设备布置状况示意图

在模型实验段正中剖面上(两强横框架之间)布置系列电阻式应变片，在该剖面前后各一个强横框架间距剖面位置对称布置几个应变片以验证数据可靠性[9]，通过动态应变仪采集不同波浪状况(不同时刻)各测点应变状况，根据实验材料力学特性推算其应力分布状况.实验在迎浪状态下进行，左右舷应变理论上是相同的，因此右舷测点布置得较密，左舷测点布置得相对较疏，模型实验段正中剖面应变测点布置见图4.

图4 应变片测点布置

2.3 实验工况

虽然实验模型材料选强度相对较弱的3105-O态铝合金，但还是有相当的承载能力，为探究其在波浪中的崩溃特性，遭受的外载荷须比结构的承载能力要大.考虑到造波水池的造波能力，须在实验模型两端施加固定压载以造成一定的静水弯矩，同波浪弯矩合在一起引起实验模型崩溃.若固定压载不足，在现有造波能力下，外载荷不足以使模型结构发生崩溃；但如果固定压载过多，较小波高下模型结构即发生崩溃，崩溃过程及崩溃特性难以充分展现.经过数次试算及预实验，最终确定在模型前后端面施加280 kg固定压载，在波长6.75 m、波高达130 mm时模型发生崩溃，揭示其逐次崩溃特性.实验工况见表2.

表2 实验工况

3 实验结果及分析

3.1 崩溃模态

实验在模型两端施加280 kg固定压载的情况下进行，波高从100 mm逐步增加到110 mm，120 mm，当波高达到130 mm时，波峰从艏向艉移动，当波峰接近船舯位置时，模型结构发生崩溃，丧失承载能力.崩溃模态表现为整体中拱弯曲变形以及中部实验段底板在水压及纵压联合作用下的局部变形.崩溃时模型整体纵向变形见图5，其中下部虚线为原始状态，上部虚线为变形状态.中部实验段底板受到船底水压作用和模型中拱引起的纵向压缩载荷作用，其崩溃模态为水压引起船底板架变形和板格变形以及纵压引起板架变形和板格屈曲变形的合成.水压作用下，船底板架变形呈一个半波正弦模态，板格变形呈柱状模态；纵向压缩载荷作用下，船底板架变形呈一个半波正弦模态，板格变形为三个半波正弦模态.中部实验段底板崩溃模态见图6.

图5 整体崩溃模态

图6 中间实验段船底崩溃模态

实验中随着波峰由船首向船舯移动，中部实验段受到的中拱弯矩不断增加，船底构件在总纵弯曲压应力和水压力引起的局部弯曲压应力联合作用下先发生屈曲，继而舷侧结构靠近船底部分也发生屈曲，随后船底结构发生屈服，随着中拱弯矩的进一步增加，甲板结构也发生屈服，整体结构达到极限状态，丧失承载能力，崩溃发生.

3.2 船底纵向应力分布

实验中随着波峰的移动，各应变测点的测量值也会随着变化，图4中典型测点11的纵向应力随时间变化关系见图7.应变测点的测量值呈周期性变化，应力基本上围绕着平均值-32.15 MPa，变化幅值约为9.65 MPa，周期约为2.1 s.实验中波浪周期为2.1 s，与应变测点变化周期相同；应力平均值-32.15 MPa为静水弯矩引起，变化幅值9.65 MPa为波浪载荷引起.

图7 测点11应力实验测量值

模型结构崩溃时刻中间剖面船底各测点的纵向应力沿船宽方向分布状况见图8，中间部分(中间两块板格)呈拉应力状态，靠近舷侧部位(舷侧板格)呈压应力状态，呈“几”字形对称分布，应力变化范围为-41.4～13.3 MPa.最大拉应力发生在纵中剖面位置，最大压应力发生在舷侧板格中央.

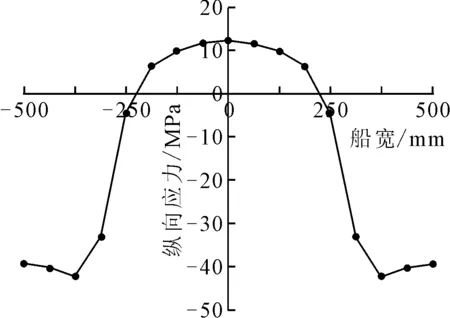
图8 崩溃时刻沿船宽方向船底位置纵向应力分布

实验中船底结构受到纵压和水压的联合作用，为探究崩溃时刻船底应力分布的特性，对实验船模结构进行了纵压单独作用及水压单独作用时的有限元计算分析，计算结果见图9所示.在两端压载形成的纵压载荷作用下，船模呈现中拱状态，船底板受压，同一剖面沿船宽方向船底各位置处的纵向压应力基本相同(图9中虚线所示)；在水压作用下，船底板架发生整体变形，同时板格也发生局部变形，在二者联合作用下，船中剖面沿船宽方向船底各位置处的纵向压应力分布见图9中实线所示.由图9可知，是由于水压作用使得船底各位置处沿船宽方向的纵向压应力呈“几”字形分布.

图9 纵压和水压单独作用时船底位置纵向应力沿船宽方向分布状况

3.3 极限承载能力

船模结构在两端固定压载及波浪载荷作用下，在各构件处产生内应力，将各剖面位置各构件的纵向应力积分即可得到纵向内力，纵向内力沿剖面中和轴积分可得到剖面垂向弯矩；根据船底和甲板位置平均纵向变形差值可算出该剖面的转角.随着波峰由船首向船舯运动，船模结构正中剖面受到的垂向弯矩逐渐增大，当波峰接近船舯时，实验船模所受到的垂向弯矩比其结构耐力要大，模型丧失承载能力而发生崩溃.实验得到的船中剖面弯矩-转角关系曲线与数值计算值比较见图10.

图10 船中剖面弯矩-转角关系曲线

在对实验船模进行数值计算时(非线性有限元计算)，没有考虑初始变形和焊接残余应力的影响，这样得到极限剖面变矩值为4.236×106N·mm，较实验值4.044×106N·mm要偏大4.75%.若数值计算时不计水压力作用，则极限剖面变矩值高达5.430×106N·mm，较实验值要大34.27%.水压力的作用加剧了船底板和舷侧结构的面外变形，使结构更早的发生屈服，从而降低结构的极限剖面变矩.正如Lehman[10]指出的那样，实际的船体结构并不是在强制位移或转角的作用下发生崩溃的，是分布的压力或者力的作用使船体结构发生崩溃.因此，传统的通过施加强制转角的方式得到的极限弯矩并不能准确代表船体结构实际的承载能力；为使船体结构在实际航行中安全可靠，极限剖面变矩计算时须计入水压力的作用[11-12].

4 结 论

1) 船体结构在波浪中受到静水载荷和波浪载荷的联合作用，随着波峰位置的不断移动，使得船体结构典型剖面受到的弯矩达到最大，船底构件在总纵弯曲压应力和水压力引起的局部弯曲压应力联合作用下先发生屈曲，继而舷侧结构靠近船底部分也发生屈曲，随后船底结构发生屈服，随着弯矩的进一步增加，甲板结构也发生屈服，整体结构达到极限状态，丧失承载能力，发生崩溃.

2) 在船体结构发生崩溃时，船底各点纵向应力沿船宽呈“几”字分布，这是总纵压力与水压力共同作用的结果.纵压作用下，同一剖面沿船宽方向船底各位置处的纵向压应力基本相同；水压作用下，船底板架发生整体变形，同时板格也发生局部变形，船底各位置处沿船宽方向的纵向应力分布呈“几”字形.

3) 水压力的作用加剧了船底板和舷侧结构的面外变形，使结构更早的发生屈服，从而降低结构的极限剖面变矩.为使船体结构在实际航行中安全可靠，极限剖面变矩计算时须计入水压力的作用.