考虑二阶发电机模型的非线性水轮机调节系统动力学分析
2020-12-17曹林宁吴道科
曹林宁,吴道科,李 兵,张 赫
(1.河海大学能源与电气学院,南京210098;2.安徽绩溪抽水蓄能有限公司,安徽 绩溪 245300)
0 引 言
水轮机调节系统实质上是一种非线性非最小相位系统,涉及水力、机械和电气等诸多非线性因素[1, 2]。作为水电站整体结构中的一个关键部分,水轮机调节系统的稳定性问题引起水电行业内的众多关注,关系到发电机组甚至是所在电网的安全运行[3, 4]。以往的线性控制理论可近似处理水力发电机组小波动分析情况,但是当系统处于较大扰动时则需要采用更贴近实际的复杂非线性水轮机调节系统。Hopf分岔作为非线性系统动态特性中的一种重要分岔问题,在电力系统的分岔与混沌问题等非线性动力学研究中得到广泛应用[5-7]。1992年IEEE在单机单管无调压室基础上提出了一种非线性水轮机调节模型[8];凌代俭等则将Hopf分岔理论应用到非线性水轮机调节系统中,得到了系统关于PID控制参数的稳定域并为水电站中的低频振荡问题提供了一种合理解释[9, 10];陈帝尹、把多铎等建立了复杂管系和带简单调压室的水轮机调节系统模型,并以调速器参数进行非线性动力学分析[11, 12];张醒、曹春建等建立了考虑分数阶PID调速器模型的水轮机调节系统并对其进行稳定性分析[13, 14];郭文成、杨建东等则基于变高顶尾水洞模型建立非线性水轮机调节系统并对该系统进行Hopf分岔分析[15]。这些研究中大都关注于引水管道和水轮机部分的非线性特性,对于发电机部分往往仅考虑其转动惯量而选择采用简单一阶模型从而忽略了发电机非线性本质的影响。为了进一步的体现水轮发电机调节系统的非线性特质,本文在考虑弹性水击和非线性水轮机特性的基础上,引入发电机转子二阶动态模型,综合考虑了水轮发电机调节系统各个方面非线性因素的影响,建立了一个全新的非线性水轮发电机调节系统模型,并运用Hopf分岔直接判据结合数值模拟分析了不同调速器PID参数下的水轮发电机调节系统动态特性。
1 非线性水轮机调节系统建模
本文建立的非线性水轮机调节系统模型结构如图1所示,其中水轮机、引水系统和发电机及负载部分均采用非线性方程表示。根据水力学知识,不论是水体本身还是管道都是具有弹性的,所以当引水管道较长时,需要考虑弹性效应对水轮机调节系统的动态性能产生的影响。本文采用的弹性水击模型中,有压过水系统的传递函数为非线性双曲正切函数:
Gh(s)=-2hwth(0.5Trs)
(1)
式中:hw为引水管道特性系数;Tr为水击相长。
为了便于研究,将上式泰勒展开并忽略高阶次数项得:
(2)
将上式改写成微分方程式:
(3)
用状态空间式表示为:
(4)
且有:
(5)

对于混流式水轮机,通常可以用含有六个传递系数的式子来表达其动态特性:
(6)
在线性水轮机模型中一般认为上式中六个传递系数为常数,本文采用的非线性水轮机模型中将这六个传递系数改写成非线性表达式[16]:
(7)
式中:eym、eqym、eωm、eqωm、ehm和eqhm可由水轮机力矩特性求得。
将式(6)中的第二式两边同时对时间求导并结合式(5)可得:
(8)
对于发电机部分,本文采用一个发电机转子二阶动态模型,该模型在研究机电联合过渡过程和电磁暂态过渡过程中被广泛使用,模型如下:
(9)
式中:δ为发电机转子的角度;ω为发电机转速相对偏差值;ω0=2πf0;D为发电机阻尼系数,取值范围一般在0~3.0;Tab为机组惯性时间常数。
若在发电机阻尼系数中考虑转速变化对力矩的影响,则可以近似认为发电机电磁功率和电磁力矩相当,即:
me=Pe
(10)
其中电磁功率为:
(11)
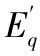
液压随动系统动态特性为:

(12)
式中:Ty为接力器反应时间常数;u为调节器输出。
本文考虑实用并联PID型水轮机调速器,其输出形式为:
(13)
式中:r为水轮机调节系统转速(频率)参考输入;kp、ki、kd分别为比例、积分和微分增益。
假设r=0,即在不考虑频率扰动情况下研究非线性水轮机调节系统动态特性,则式(13)可改写为:
(14)
综合式(4)~(14),得到本文的六维水轮机调节系统非线性模型为:
(15)
2 数值模拟分析
2.1 六维自治系统Hopf分岔直接判据

λ6+p5λ5+p4λ4+p3λ3+p2λ2+p1λ+p0=0
(16)
如果当v=v*时有:
(1)Δi>0(i=1,2,3,4),Δ5=0,式中Δi(i=1,2,3,4,5)为该特征方程的Hurwitz行列式;
(2)k02UZ≠VW,其中:
(17)
则当|v-v*|充分小时,该系统将会在v*的某一侧出现Hopf分岔现象。利用该直接判据分析本文提出的六维非线性水轮机调节系统随PID控制参数变化的分岔特性以及稳定性。
2.2 系统稳定域分析
将以上数值代入式(15)并在平衡点x=(0;0;0;0;0;0)处求取系统的雅可比矩阵(该矩阵过于繁冗此处暂不列出),该雅克比矩阵对应的特征方程式各项系数如下所示:

(18)
根据六维Hopf分岔直接代数判据可以得到系统发生Hopf分岔时调速器PID参数kp、ki、kd临界值所构成的空间曲面。为方便分析,现将其投影到二维平面上观察。如图2所示,即为在kp-ki平面上不同kd取值时分岔临界点所构成的曲线。
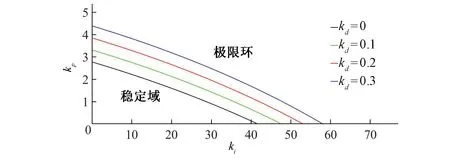
图2 不同kd取值下系统分岔临界点构成的曲线
通过计算该非线性系统在分岔点处的曲率系数β2<0可知此时分岔为超临界Hopf分岔。对于超临界Hopf分岔,在分岔参数v-v*>0时将会出现稳定极限环而当分岔参数v-v*<0时系统则稳定。根据图2可知:在分岔临界点构成的分岔曲线内侧即为系统稳定域,此时的平衡点是一个逐渐稳定的平衡点,而在分岔曲线外侧的附近范围系统将收敛至稳定极限环。当调速器的PID参数从稳定域穿过分岔曲线至极限环区域时,系统就会产生Hopf分岔。从图2还可以看出,当系统参数kd逐渐增加时,系统的稳定域范围也会增大。这说明微分增益增加能够在一定程度上提高系统稳定性,原因是微分环节具有超前调节功能,能够有效的抑制误差变化。
2.3 系统Hopf分岔分析
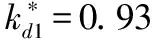
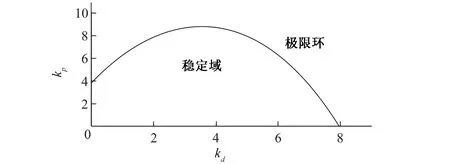
图3 ki=0.2时系统分岔临界点构成的曲线
对系统(15)用ode45函数进行数值求解并采用局部最大值法作出系统状态变量分岔图。如图4所示,图中纵坐标选择水轮机调节系统转速偏差相对值ω来观察系统分岔特性,横坐标即为分岔参数kd。
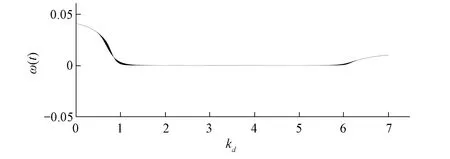
图4 机组转速ω随kd变化的分岔图
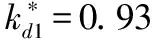
在图3所示的PD平面上选择几个不同位置的点,分析无频率扰动非线性水轮机调节系统转速时域响应和相轨迹变化。当kp=6、ki=0.2,分岔参数kd=5时,系统的状态变量时域响应和相轨迹图如图5所示,从图5中可以看出系统在经过一段时间后最终收敛到平衡点位置,表示在此PID调速器控制参数下的非线性水轮机调节系统的稳定性较好,在系统受到扰动时能够在一定时间内重新达到稳定状态。

图5 稳定域内系统动态特性
当分岔参数取kd=6.5时,系统的状态变量机组转速时域响应和相轨迹图如图6所示,机组转速最终处于等幅振荡的状态,而系统相轨迹也将收敛至稳定极限环。
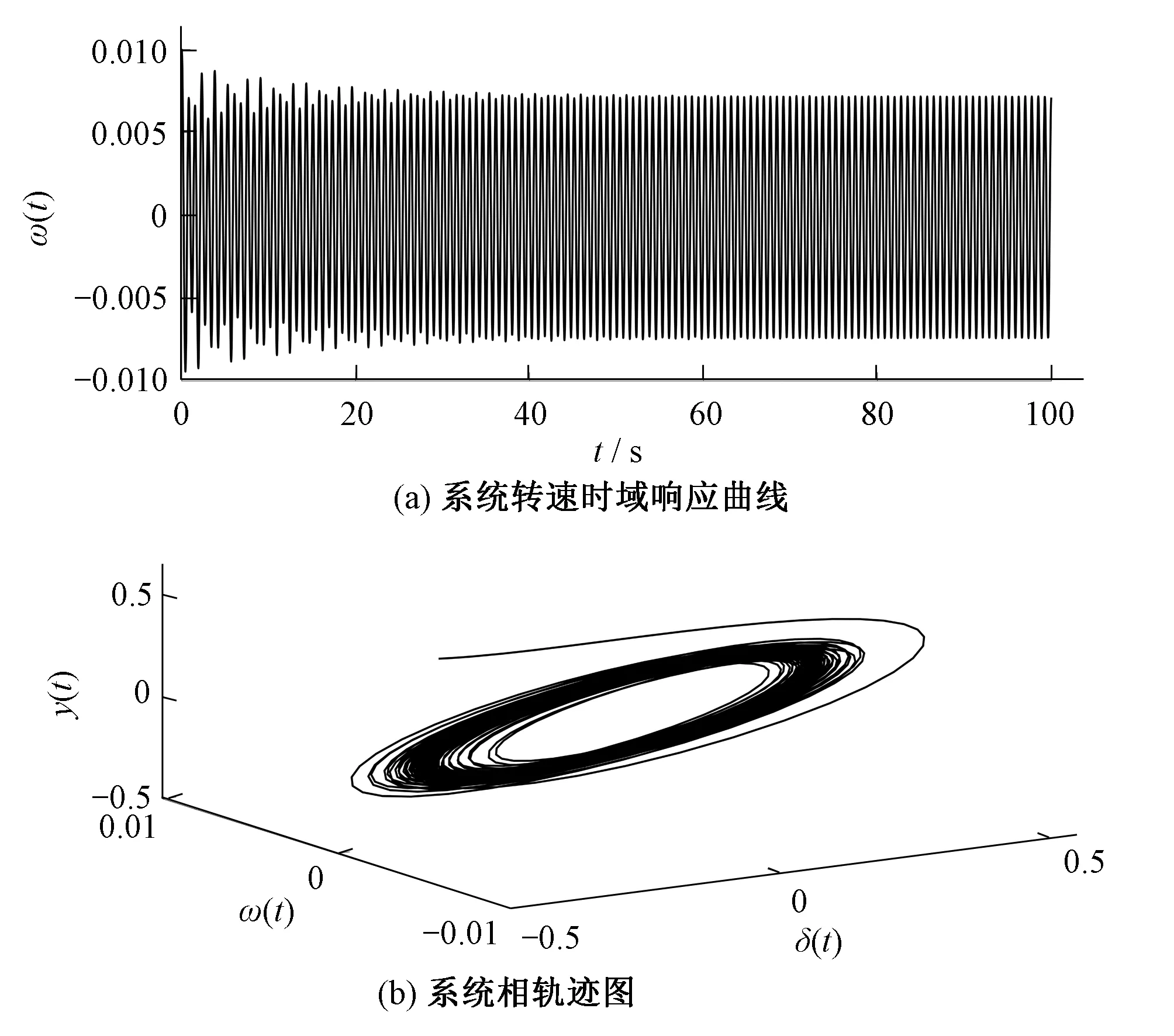
图6 极限环时系统动态特性
2.4 系统混沌特性分析
从图7所示的分岔图可以看到,当分岔参数kd在超过分岔临界值而继续增大时,系统状态变量会经历Hopf分岔、倍周期分岔直至混沌的变化过程。选择参数kp=6、ki=0.2、kd=8.5时分析机组转速时域响应和系统相轨迹曲线如图8所示。从图8中可以看到,当非线性水轮机调节系统进入混沌状态后,系统不再收敛至稳定状态而表现出复杂的动态特性,从相轨迹曲线看,系统虽然保持在一定的范围内运动但是在局部区域却又表现出严重的无序性,说明系统此时是不稳定的,所以在电站实际运行中需要防止调速器参数处于混沌区域从而提高水轮机调节系统在大小波动过渡过程中的稳定性,避免事故的发生。
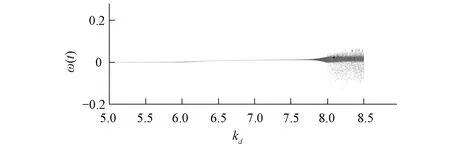
图7 混沌区域系统分岔图

图8 混沌区系统动态特性
混沌现象体现了非线性系统中类似随机的复杂状态,随着时间的推移系统表现出不可预测性,即系统的演变过程对于初始状态异常敏感。如图9所示,选择用机组转速相对偏差ω作为系统状态变量来观察混沌区域系统的初值敏感性。选用两组区别很小的系统初值(0.01,0.01,0.01,0.01,0.01,0.01)和(0.01,0.01,0.01,0.01,0.0101,0.01)进行时域响应分析,结果显示即使很小的初值变化也会导致机组转速随时间变化的巨大差异。
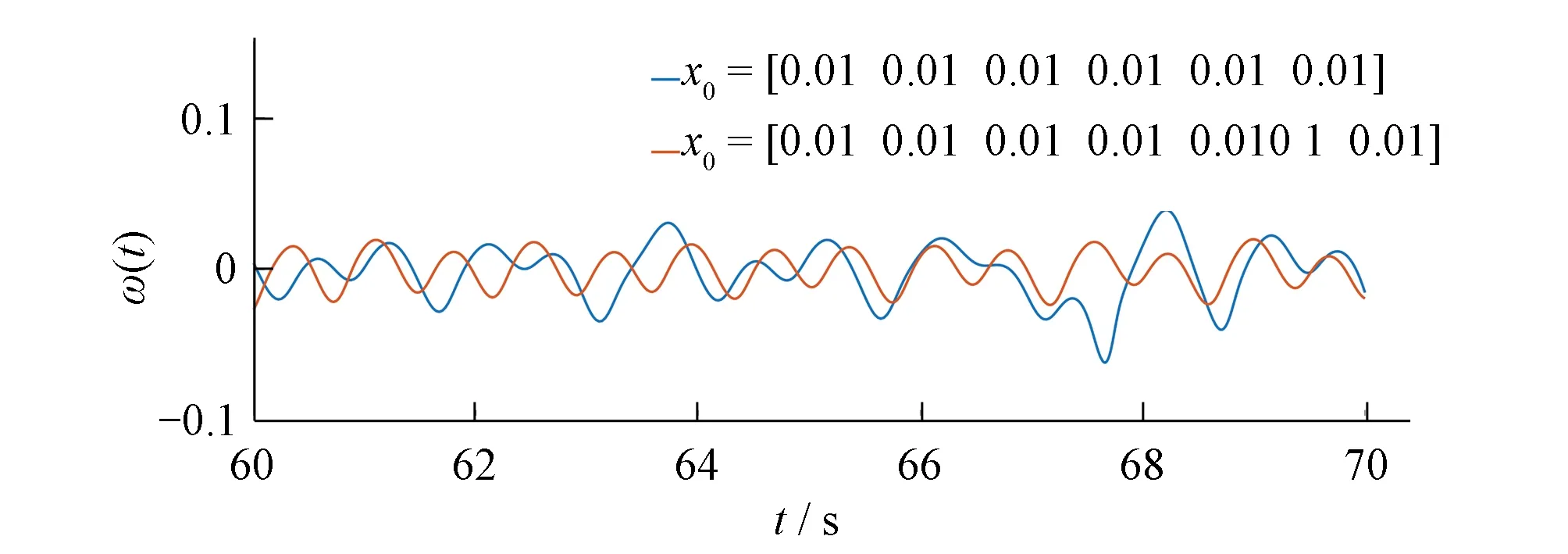
图9 初值敏感性分析
3 结 语
本文在考虑引水管道和水轮机非线性因素的基础上,引入发电机转子二阶动态模型同时忽略系统频率扰动,从而建立了一个完整的六维水-机-电联合非线性调节系统,该非线性水轮机调节系统相较于一般的线性水轮机调节系统能更好地体现出水轮机调节系统的复杂特性,对电站实际运行具有更优的指导和参考价值。文中选择以常见的PID调速器参数为控制参数,利用六维非线性系统Hopf分岔直接判据得到了能使该系统稳定运行的参数范围即系统稳定域,并通过分岔图以及系统动态仿真表明随着PID参数逐渐超出分岔点,系统的拓扑结构将会发生变化,原本渐进稳定的非线性水轮机调节系统会出现等幅振荡甚至是严重失稳的现象。因此,为了提高非线性水轮机调节系统运行的稳定性和避免机组振荡问题的发生,控制参数的选择应尽量远离分岔点。
□
