基于多域联合的无人机集群认知抗干扰算法

刘春玲,刘敏提,b,丁元明,b

(大连大学 a.信息工程学院; b.通信与网络重点实验室,辽宁 大连 116622)

0 概述

在未来空战中,无人机(Unmanned Aerial Vehicle,UAV)集群作战将是重要的作战形式之一,针对其高动态、网络拓扑结构多变等特性,采用分布式网络结构可提高无人机集群网络的抗毁性。此外,实现信息安全、可靠传输是其完成任务的关键,确保无人机之间的可靠通信,将成为一项重要的研究内容[1]。

近年来,如何有效对抗智能性干扰与提高通信安全已成为研究热点[1]。在抗干扰技术研究中,认知抗干扰算法已成为研究热点方向之一[2],该算法可归纳为如下两类:一类是基于强化学习理论[3]进行可用信道的选择,主动规避干扰信道,从而实现频域抗干扰。文献[4]提出基于协作Q学习(Q-Learning,QL)的信道选择算法,该算法可提高数据传输成功率,但当状态空间规模较大时,其面临维数灾难的问题[5-6]。针对该问题,文献[7]提出将深度Q网络(DQN)在线学习算法应用于信道选择。当信道数量较多时,文献[8-9]利用演员-评论家(Actor-Critic,AC)算法进行信道选择,但是该算法存在方差较大以及稳定性较差的问题。另一类是基于博弈论的方法[10-12],根据敌我双方的竞争关系,建立功率域抗干扰博弈模型,通过求解博弈均衡得到最佳传输功率,实现从功率上压制干扰信号以达到抗干扰的目的。以上算法均是仅从单个频域或者功率域角度考虑,针对智能性干扰攻击的灵活性较差[13]。

为提高网络抗智能干扰的能力,本文将功率域和频域抗干扰方法相结合,基于优势演员-评论家(Advantage Actor-Critic,A2C)[14]与Stackelberg博弈(Stackelberg Game,SG),提出一种多域联合认知抗干扰(Multiple Domain Joint Cognitive Anti-Jamming,MDJC-AJ)算法。该算法将可用信道探索问题转化为序贯决策问题,由感知到的环境频谱状态进行信道选择。根据设定的干扰容忍双阈值将信道干扰程度分为严重、中度与轻微3个等级,并对处于中度干扰等级的信道建立功率域斯塔克伯格博弈模型,通过求解博弈均衡得到最佳传输功率。与此同时,本文采用簇头协助决策方式来协助簇内信道决策成功率较低的节点,以提高网络整体感知环境的准确性与干扰信道决策成功率。

1 无人机集群网络模型

无人机集群网络采用层次结构的移动Ad-Hoc网络,当无人机的数量大于6架时,适合采用分层式结构[15]。无人机集群网络对抗智能干扰机示意图如图1所示。

图1 无人机集群网络对抗智能干扰机示意图Fig.1 Schematic diagram of UAV cluster networkresist intelligent jammer

假设网络中干扰机为J,干扰机个数为1,节点总数为NS,分簇数M=NS/NC,NC为簇内节点个数,节点i的簇内邻节点个数C-i⊂ΩS,其中,ΩS为网络节点集合。假设簇头具有较高的等级,数据处理能力最强,其在簇内则充当局部控制中心的角色,簇间节点通过所在簇的簇头转发数据进行通信。

2 多域联合认知抗干扰算法

2.1 基于A2C的频域抗干扰算法

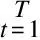
2.1.1 奖励函数

在t时刻,且无干扰机时,节点i接收信号的信干噪比(Signal to Interference-plus Noise Ratio,SINR)为γNJ(t),存在干扰机时,SINR为γYJ(t),可表示为:

(1)

(2)

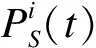
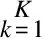
(3)

(4)

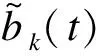
(5)

2.1.2 状态空间与动作空间

假设环境状态空间S为节点i的前一时刻感知频谱bt-1,则时刻t的状态st可表示为:

st=bt-1,st∈S

(6)

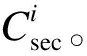
2.1.3 基于优势演员-评论家的频域抗干扰算法

AC算法是由行动者(Actor)与评论家(Critic)组成的强化学习算法,其中,Actor负责更新策略,Critic负责更新动作值函数。与AC算法相比,A2C算法通过引入基线能够降低学习过程中的方差,以较准确的动作值指导策略更新,可带来更好的求解效果。在实际应用中真实价值很难得到,一般采用函数近似法对价值和动作函数进行参数化,利用神经网络等机器学习算法求解,求解过程如下:

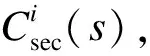
(7)

2)对于Actor而言,其目标是通过不断地更新参数w,使得其尽可能得到好的策略πw(s,a),即:

(8)

其中,d(s)对应起始状态s。

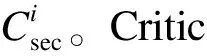
为增加模型探索能力,在模型目标函数中加入策略的熵正则化项,其可衡量概率策略分布的不确定性,且其值越大说明模型具有更好的多样性[18-19]。Actor网络的参数w基于策略梯度下降的计算方法为:

(9)

(10)

表1 信道干扰等级判定规则Table 1 Decision rule of channel jamming level

2.2 基于SG的功率域抗干扰算法

在2.1节的基础上,当上一时刻所用信道在当前时刻被判决为等级2时,则对该信道建立功率域SG模型,并通过求解Stackelberg均衡(Stackelberg Equilibrium,SE)得到最佳传输功率,实现功率域抗干扰。

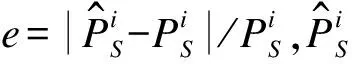
(11)

干扰机J的效用函数可表示为:

(12)

(13)

(14)

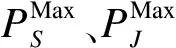
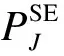
2)考虑极端情况,有以下2种情况:

(15)

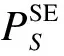
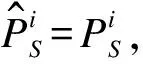
(16)

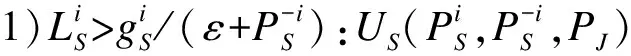
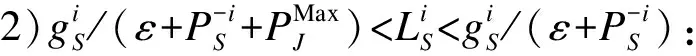
(17)

综上所述,本文提出的MDJC-AJ算法实现过程描述如下:

输入训练数据D={(si,bi)|si∈S,bi∈A},经验池E

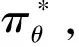
2)迭代更新。对每个智能体(节点/簇头),每幕执行以下操作:

(2)执行:利用πθ(·|s′)得到动作b′。

(4)策略更新:基于式(9),更新策略网络参数w。

(5)价值更新:基于式(10),更新策略网络参数θ。

(6)更新状态与动作:s←s′,b←b′。

3)直至达到最大迭代次数Nit,结束。

2.3 算法复杂度分析

参考文献[12],本文对MDJC-AJ算法的复杂度进行分析,结果如表2所示。

表2 MDJC-AJ算法复杂度分析Table 2 Complexity analysis of MDJC-AJ algorithm

本文算法的运算复杂度分析描述如下:

2)对于单个节点,根据策略πθ(·|s′),在每个状态下执行相应动作得到奖励值的复杂度为O(C2),C2为与策略类型相关的常数,所有节点的运算复杂度为O(NSC2),该部分对应算法迭代更新中的步骤2、步骤3。

3)对于单个节点,基于式(9)、式(10),更新参数w、θ以及状态s、动作b,运算复杂度为O(C3),C3为与每幕的时间步长或收敛迭代次数相关的常数,所有节点的运算复杂度为O(NSC3),该部分对应算法迭代更新中的步骤4～步骤6。

4)对于单个节点,根据阈值进行等级划分,运算复杂度为O(C4),C4为与阈值个数相关的常数,所有节点的运算复杂度为O(NSC4)。

5)干扰机最佳干扰功率运算复杂度为O(C5),C5为与式(15)相关的常数。

6)对单个节点,根据式(17)计算节点最佳传输功率运算复杂度为O(C6),C6为常数,所有节点的运算复杂度为O(NSC6)。

通过以上分析,可得到MDJC-AJ算法的总运算复杂度为:

Csum=Nit(O(NSC1)+O(NSC2)+O(NSC3)+

O(NSC4)+O(C5)+O(C6))

(18)

2.4 基于簇头协助的信道选择算法

由于实际环境态势的多变性以及信息的局部性,存在单个节点局部频谱感知能力有限的问题,为此引入簇头协助从节点决策方法。基于簇头协助的无人机集群网络抗干扰示意图如图2所示。

簇头协助从节点决策方法可描述为:各节点进行局部环境感知与信道决策时,若某节点所得结果无法达到期望值,则向簇头发出Help信息,簇头收到求助信息后,则向其传输无干扰信道数据信息,使其能够进行可靠通信。需要说明的是,所有节点和簇头均采用MDJC-AJ算法进行抗干扰。为了不失一般性,图2中仅详细说明第一个簇头内部抗干扰算法的实现流程。

3 实验仿真与分析

为验证本文所提算法的有效性,实验选用卷积神经网络来拟合值函数和策略函数。仿真环境为Intel®CoreTMi7-4790 CPU@3.60 GHz四核八线程处理器,采用Pytorch1.2.0深度学习框架与Matlab2018a仿真平台。

Actor网络与Critic网络基本一致,不同的是最后的全连接层[20]。Actor网络输出维度为32×1,对应32个待选信道,Critic的输出维度为1,用于计算Actor所获奖励。网络结构参数设置如表3所示。

表3 网络结构参数设置Table 3 Parameter setting of network structure

仿真1为验证本文所提算法的信道选择性能,考虑干扰机采用智能性干扰,即不同时间段干扰机干扰的信道和功率均不同,为便于分析将环境状态的时变点分别设在tchange=1 500和tchange=3 300,网络中节点个数为4,编队及所选簇头已最优。实验对文献[4]Q学习抗干扰(QL-AJ)算法、文献[8]演员-评论家抗干扰(AC-AJ)算法与本文算法的信道干扰情况决策成功率进行比较,结果如图3所示。从图3可以看出,在各个阶段内,相比QL-AJ算法与AC-AJ算法,本文所提MDJC-AJ算法的信道干扰情况决策成功率更高。

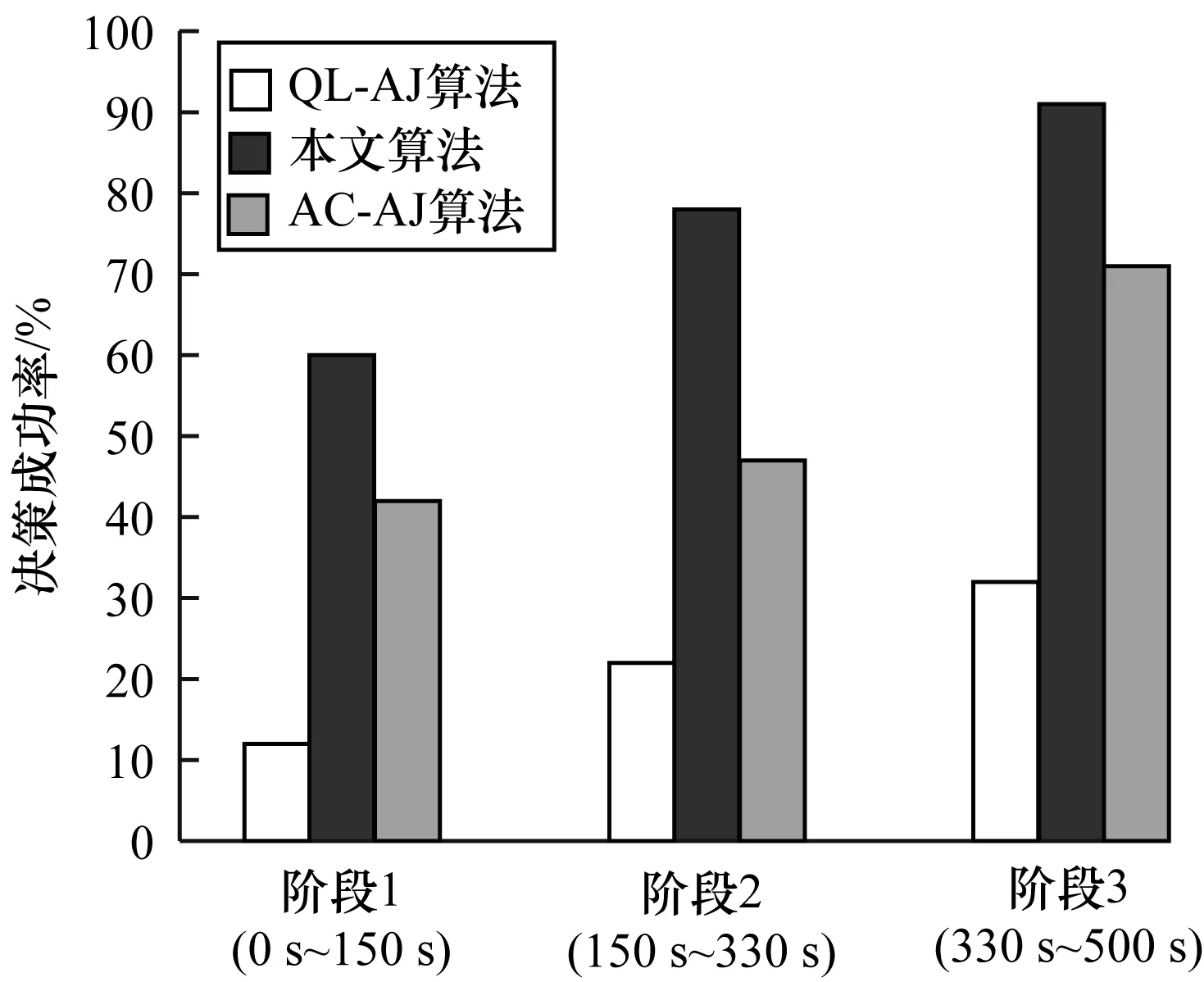
图3 3种算法的干扰信道情况决策成功率Fig.3 Channel decision success rate of jammingsituation with three algorithms

为进一步说明MDJC-AJ算法在智能性干扰情况下信道决策有效性,由仿真所得信道干扰情况判决结果,如图4所示。从图4可以看出,MDJC-AJ算法在决策出可用信道索引情况下,对信道干扰功率情况进行判决,可为功率域抗干扰提供依据。

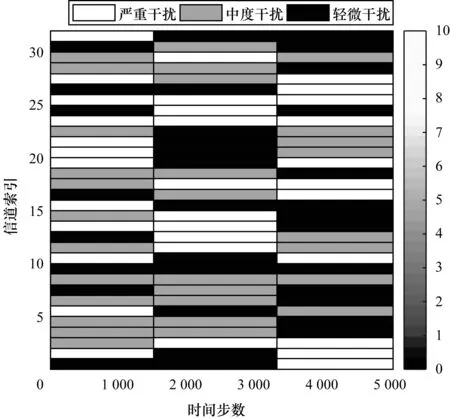
图4 MDJC-AJ算法对信道干扰情况判定结果Fig.4 Decision result of channel jamming situationby MDJC-AJ algorithm

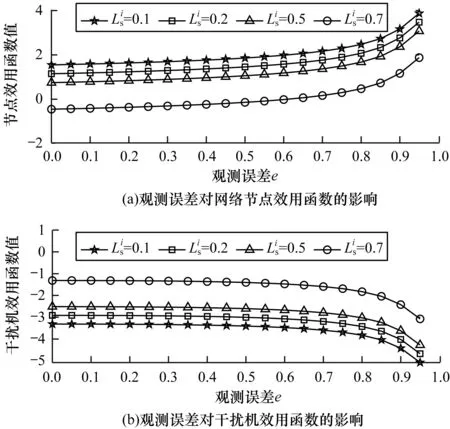
图5 观测误差e对网络节点与干扰机效用函数的影响Fig.5 Influence of observation error e on utility functionof network node and jammer

从图5可以看出,随着干扰机观测误差e的增加,节点效用函数之和呈现递增趋势,然而干扰机的效用函数呈现递减趋势。这是因为随着观测误差的增加,使得干扰机最佳传输功率偏离SE,导致其效用函数减小,干扰机观测误差等效于削弱了干扰机干扰的强度,而这将有利于提高节点效用函数,使其通信性能提升。

簇内节点个数对接收信号的SINR的影响如图6所示。

图6 簇内节点数对整体接收信号SINR的影响Fig.6 Influence of the number of nodes in a cluster onthe overall received signal SINR

仿真3实验比较了QL-AJ算法、AC-AJ算法与本文算法的抗智能干扰性能,如图7所示。从图7可以看出,在3种不同算法下,网络通信安全容量均随着训练时间的增加而不断提高,且与QL-AJ算法、AC-AJ算法相比,本文算法的网络通信安全容量更高。值得注意的是,在3个阶段的突变点,上述3种算法得到的通信安全容量均骤减,之后恢复,然而本文算法较其他2种算法恢复的更快,其原因是:由于状态空间和动作空间较大,QL-AJ算法遍历Q表所有状态的计算量庞大,算法收敛较慢;同时,AC算法利用卷积神经网络强大的计算能力,相比QL算法提高了近4倍的计算速度;另外,相比于AC-AJ算法,本文算法能够降低学习过程的方差,算法稳定性好、收敛更快,且通过联合功率域抗干扰减少信道切换的时间,同时提高了接收信号SINR,从而得到的通信安全容量更高。

图7 3种算法的抗智能性干扰性能对比Fig.7 Comparison of anti-intelligence-jamming performanceof three algorithms

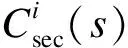
(19)

其中,|S|为系统状态个数。

为验证所提方法算法收敛性能,实验对比了QL-AJ算法、AC-AJ算法与本文算法的收敛情况。10个仿真周期的平均均方值误差如图8所示。从图8可以看出,本文算法在经过10幕左右后已经收敛,比其他2种算法的收敛性能好,且得到的平均均方值误差更小。

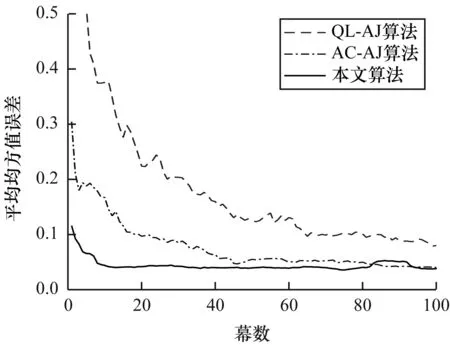
图8 3种算法的平均均方值误差变化曲线Fig.8 Average mean square error change curves ofthree algorithms

4 结束语

针对无人机集群网络对抗智能性干扰能力较弱的问题,本文提出一种MDJC-AJ算法。该算法基于A2C频域算法,利用感知到的频谱状态信息进行信道选择,以提高算法的收敛速度与信道决策成功率,并在此基础上,根据得到的功率干扰等级,利用功率域进行抗干扰,以减少信道切换时间、提高接收信号SINR。通过仿真对比QL-AJ算法与AC-AJ算法,说明本文所提MDJC-AJ算法的整体抗干扰性能较好。同时,本文采用簇头协助的方法进一步改善网络的抗干扰性能。后续将考虑实际物理场景中存在不完全观测信息的情况,开展基于贝叶斯博弈理论的抗干扰方法研究,以满足实际工程需要。