一类机械臂指数加速迭代学习控制方法

李 岩， 柴媛媛， 刘克平

(长春工业大学电气与电子工程学院， 长春 130012)

机械臂的基本控制问题是确定驱动关节位置以及跟随位置轨迹的控制算法。由于机械臂本身存在非线性和动态耦合的特性，因此控制算法的设计通常很复杂。目前，已经提出了多种用于机械臂系统的控制方法[1-2]，例如比例积分微分控制[3]和计算力矩控制[4]，它们通过反馈来实现轨迹跟踪目标。其次，自适应控制[5]、变结构控制[6]和模糊控制[7]等控制算法也经常被研究人员应用于机械臂控制中。但是，在机械臂系统应用上述算法时会导致相同的跟踪误差一次又一次地出现。针对不确定性和强非线性耦合的动态系统的控制问题，迭代学习控制(iterative learning control, ILC)[8]作为一种有效的控制策略，可以进行复杂建模，适用于具有重复性质的机械臂系统[9-12]。

在实验中，使用ILC时，机器臂系统在每次迭代开始时以相同的初始条件启动，因此机械臂每次运行时都需要重置系统的初始条件[13-16]。为了抑制初始条件对实验结果的影响，目前，Bouakrif[17]提出了一种微分(differentiation, D)型ILC，用于具有外部干扰的刚性机械臂的轨迹跟踪问题，并具有初始状态算法。因为初始状态值可以经由迭代自动获得，因此，避免了在每次迭代时需要选择初始状态值。

加速迭代学习收敛速率也是众多学者重点研究的科研目标。Wang等基于传统的D型ILC控制律，利用误差积分项和比例项抑制初始条件对控制结果的影响等[18]。但是，它没有考虑系统存在干扰时是否仍然收敛到零的情况。为加快迭代学习控制律的收敛速度[19-21]，郭文雅[22]在非扩张算子迭代算法中对算法收敛速度进行研究，使其控制算法具有更加快速的收敛速度。兰天一等[23]采取区间可调的变增益加速迭代学习控制算法，处理线性时不变系统，以加快ILC算法的收敛速度。并且在此基础上，兰天一等[24]以比例微分(proportion differentiation, PD)型为例提出在区间内可调的加速迭代学习控制算法，通过可调节区间证明Lebesgue-p范数下的加速迭代学习控制，在设计的修正区间内学习增益进行实时修正，区间外无修正的方式加快系统收敛速度，并通过 Young不等式给出收敛证明。李岩等[25]设计了一种PD型控制律，随着迭代次数的不断增加,通过在区间内对增益矩阵进行实时修改来缩短修正区间，进而达到加快收敛速度的目的。

在前期工作的基础上[25]，现提出一种无需重置条件下加速迭代学习控制方法。首先，利用控制算法使每次迭代时的初始值无需重置。其次，利用指数变增益加速迭代学习控制律，采用2自由度机械臂系统作为仿真验证对象，通过对比有无加速收敛算法仿真实验，验证本文所提出算法的可行性及有效性。最后，将该算法在Quanser机电一体化运动控制实验平台上应用，验证本文提出算法的实用性。

1 问题的提出

考虑n自由度机械臂动力学模型：

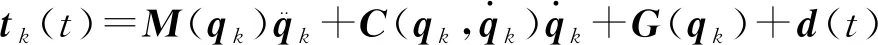
(1)

系统动力学模型[式(1)]具有以下性质：

性质1惯性矩阵M(qk)是正定有界矩阵，满足：

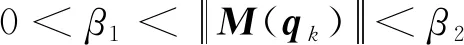
(2)

性质2惯性矩阵M(qk)满足全局Lipschitz连续条件：

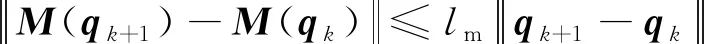
(3)

式(3)中：lm为正数。

性质3重力矩阵G(qk)满足全局Lipschitz连续条件：

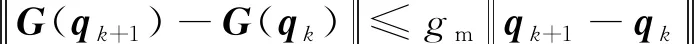
(4)

式(4)中：gm为正数。

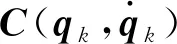
(5)

引理1[26]对于连续变量

z(t)=[z1(t),z2(t),…，zn(t)]∈Rn,t∈[0,T]，可以得到向量值函数z的λ范数范围，即不等式：

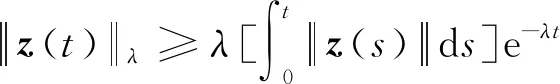
(6)

式(6)中：λ为一实数。

引理2[27]考虑连续函数f(x,y)，其中x∈Rp，|x|≤ρi,ρi≥0,1≤i≤p，y∈Rq，|y|≤μi,μi≥0,1≤i≤q，因此存在L(y)使：

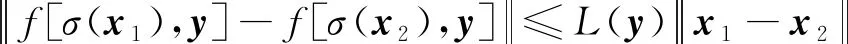
(7)

基本假设：

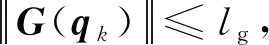
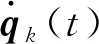
2 无需重置条件加速迭代学习控制器设计

对于具有外部干扰的机械臂系统，设计指数变增益PD型迭代学习控制律为

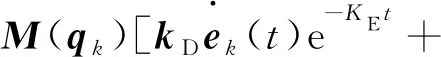
kPek(t)e-KEt]+τk(t)

(8)

无需重置初始条件需满足等式：

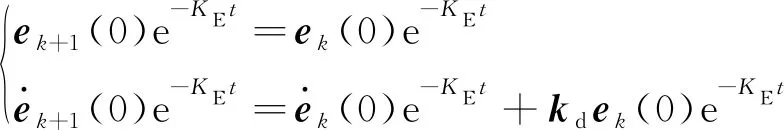
(9)

式(9)中:ek=qd-qk;KE为修正因子;kD、kP是对称正定矩阵。

机械臂闭环系统是稳定的，需满足：

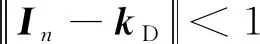
(10)

则

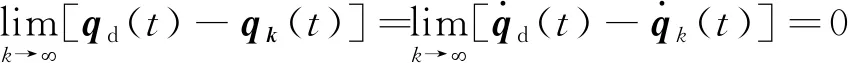
(11)

为了方便讨论，令M(qk)≡Mk，G(qk)≡Gk。

根据式(1)，可以得出:

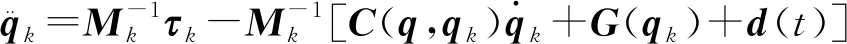
(12)

使

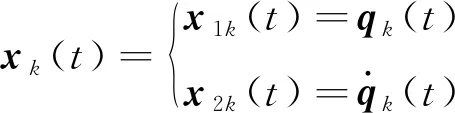
(13)

根据式(12)和式(13)，得：

(14)

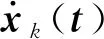
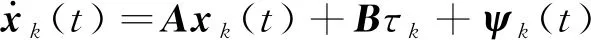
(15)

对式(15)求解一般解xk(t)为

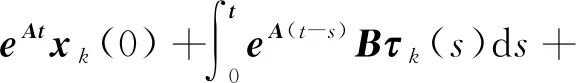
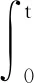
(16)

式(16)中:eA(t-s)是状态转移矩阵。

将式(8)代入式(16)，得到：

xk+1(t)-xk(t)=eAtK1ek(0)e-KEt+

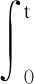
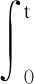
(17)

式(8)和式(17)通过分步积分公式得到表达式

xk+1(t)-xk(t)=K1ek(t)e-KEt+

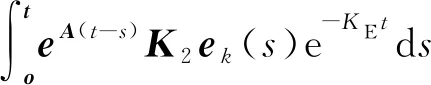
(18)

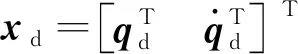
εk+1-εk=-K1ek(t)e-KEt-

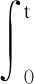
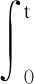
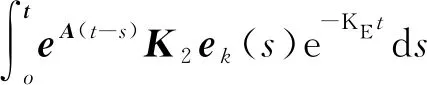
(19)

在式(19)“=”两边同时取范数，存在不等式：

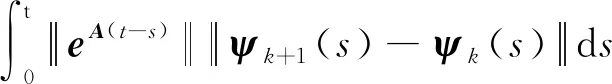
(20)

式(20)中：

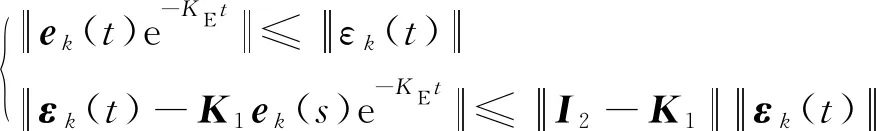
(21)

式(21)中：I2=[InIn]2。

因此，可以得到不等式：

‖εk+1(t)‖≤‖I2-K1‖‖εk(t)‖+

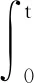
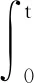
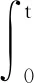
(22)

为了简化式(22)，令

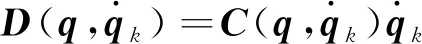
(23)

根据式(15)和式(23)，可以得到:

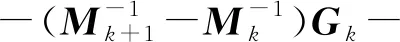
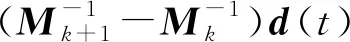
(24)

根据式(23)、式(24)以及性质1～性质4、引理2和假设1～假设3，可以得到：

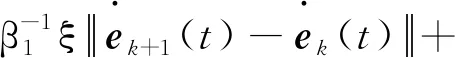
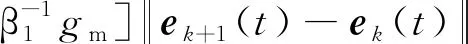
(25)

因此，

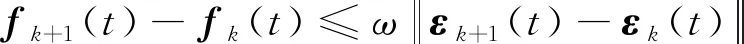
(26)

根据式(22)和式(26)，可得：

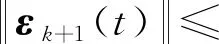
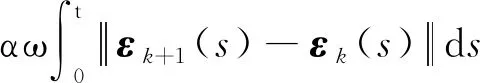
(27)

式(27)中：

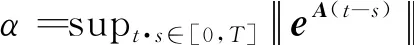
式(27)两边乘e-λt，根据引理1，可以得出：

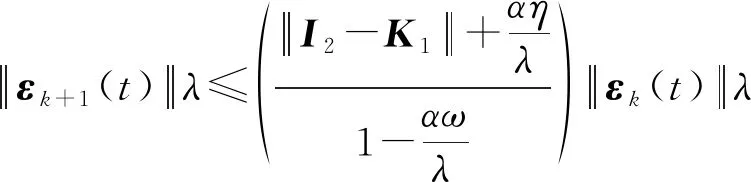
(28)

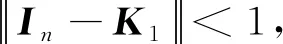
(29)

因此，根据式(28)可得：

(30)

根据式(29)和式(30)，可以得出：

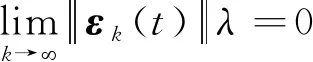
(31)

从而得出结论

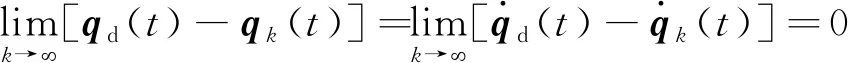
(32)

3 仿真实验结果及分析

为验证无需重置条件下加速迭代学习控制算法的可行性和有效性，利用MATLAB对2-DOFs机械臂系统进行仿真实验，2-DOFs机械臂模型如图1所示。Matlab代码是在MatlabR2014a环境下运行实现，采用如下机械臂系统动力学模型进行仿真：

M(q)=

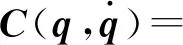
G(q)=

仿真实验时各参数为m1=2 kg,m2=2 kg,l1=0.6 m,l2=0.6 m,lc1=0.4,lc2=0.4,I1=0.1,I2=0.1期望轨迹为qd1=sin(4πt),qd2=sin(4πt)

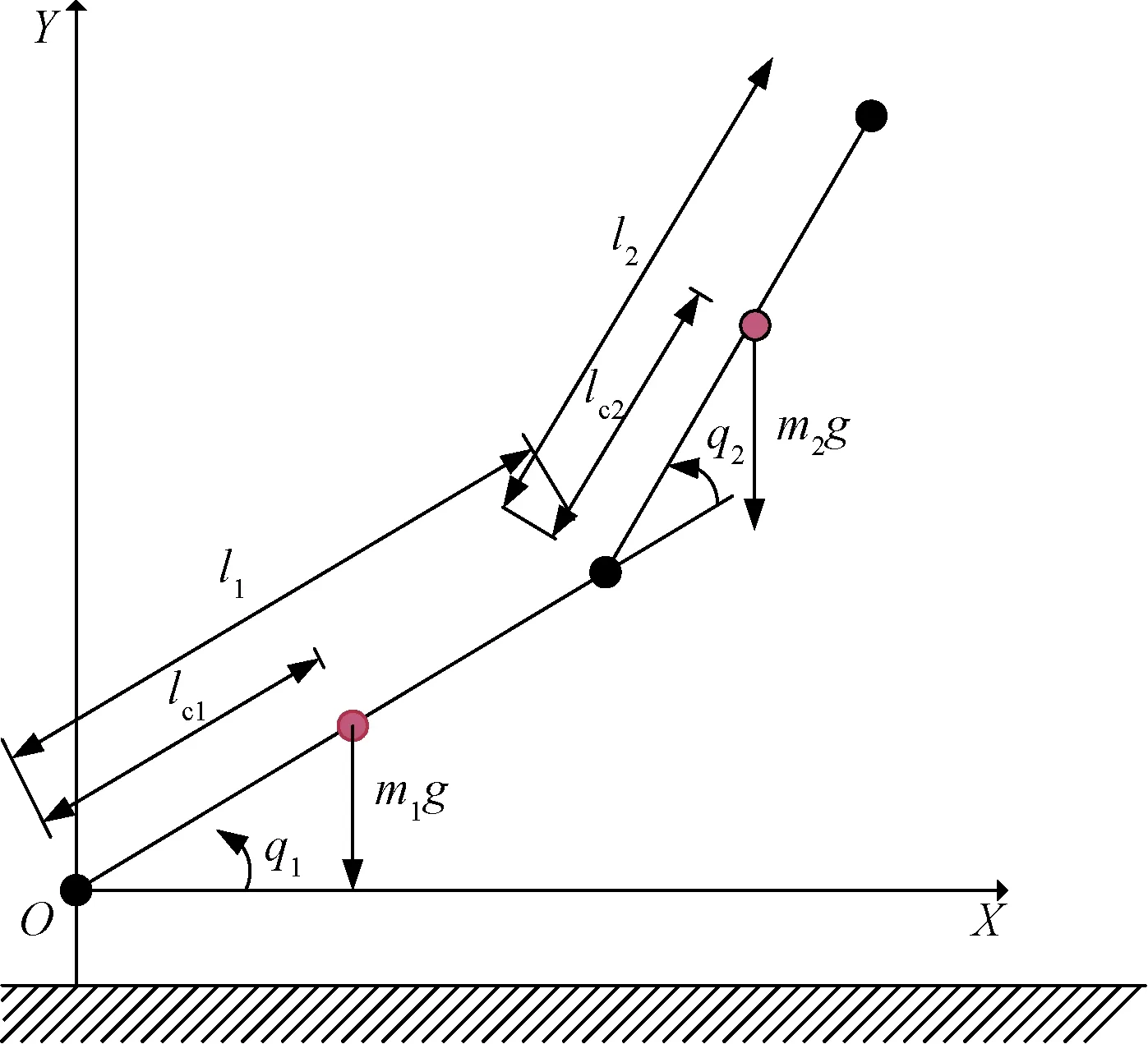
图1 二自由度机械臂系统Fig.1 The 2-DOFs manipulator

本节在两种不同类型的外部干扰下，利用MATLAB对2-DOFs机械臂系统进行仿真实验。

3.1 外部干扰为正弦函数

外部干扰为d1(t)=sin(30kπt)，d2(t)=sin(30kπt)。仿真参数：KE=0.1，kP=diag{5,5}，kD=diag{0.75,0.75}。

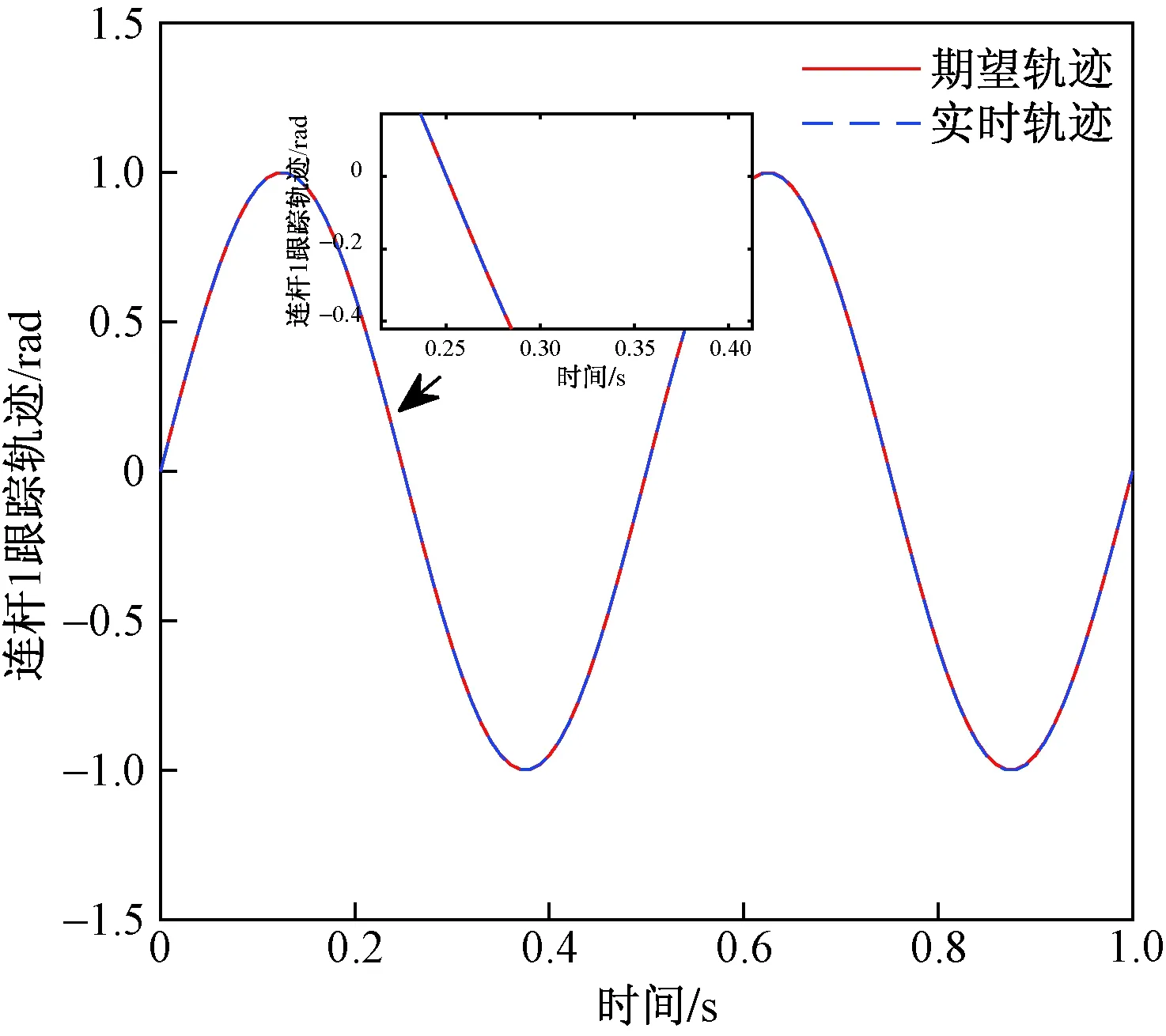
图2 连杆1的跟踪曲线(正弦函数)Fig.2 Trajectory tracking of connecting rod 1 (sine function)

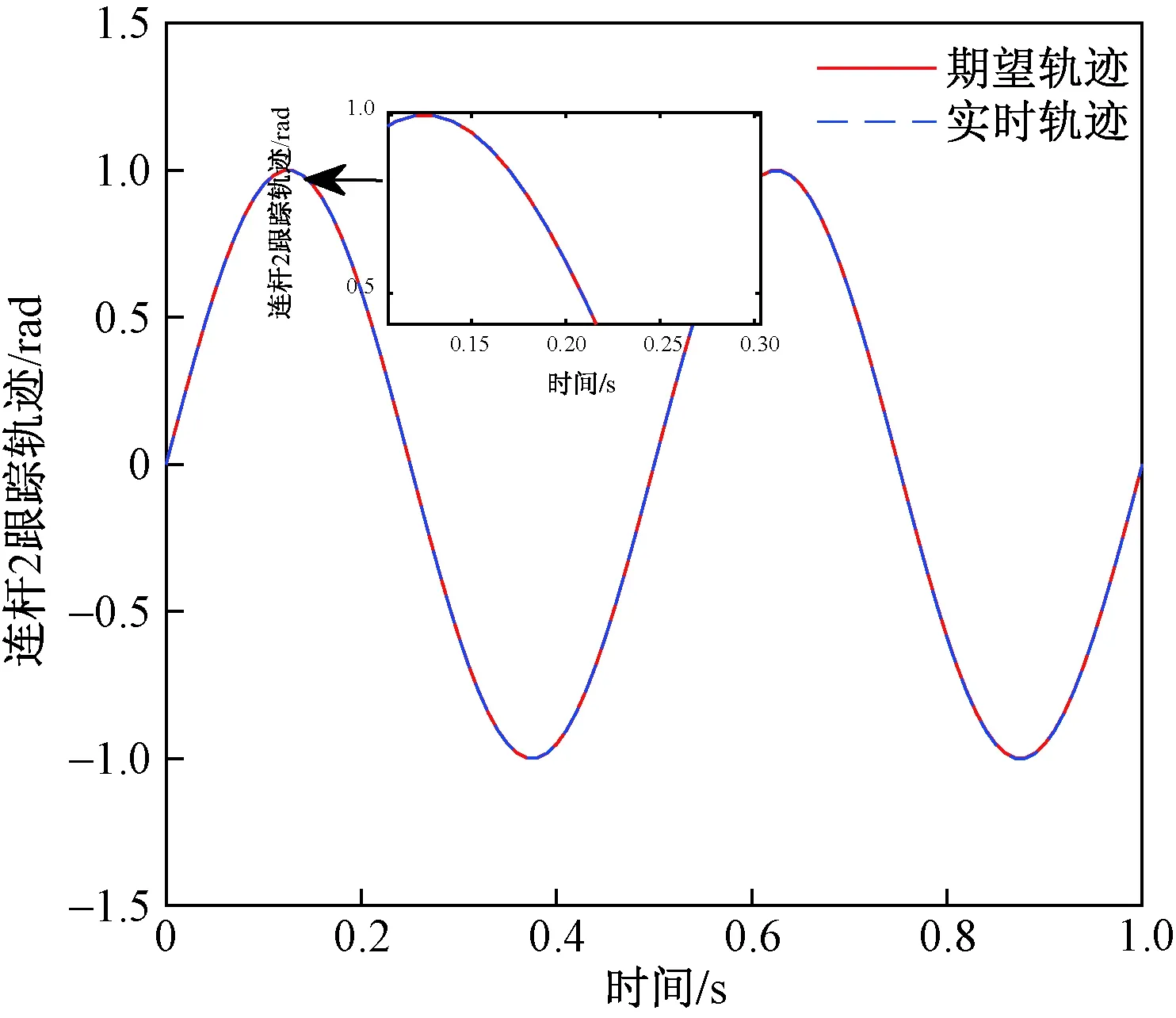
图3 连杆2的跟踪曲线(正弦函数)Fig.3 Trajectory tracking of connecting rod 2 (sine function)

图2和图3分别为机械臂系统的连杆1(q1)和连杆2(q2)经过20次迭代后曲线图。从中可以得出，机械臂的每个输出轨迹在无需重置条件加速迭代学习控制算法下，经过20次迭代后能完全跟踪其相应的期望轨迹。

图4为2-DOFs机械臂系统跟踪误差随迭代学习次数变化的曲线。在5次迭代范围内，机械臂系统每个连杆的跟踪误差减少速度较快，在经过17次迭代后可以完全跟踪上期望轨迹，表明无需重置条件加速迭代学习控制算法的收敛性。

为了便于比较分析，在相同仿真条件下，2-DOFs机械臂系统在无加速收敛条件下，跟踪误差数值变化曲线如图5所示。通过对比两组仿真实验，可以得出在本文提出的指数加速收敛算法下，机械臂系统连杆1跟踪误差和连杆2跟踪误差的数值在17次迭代后可收敛到零的邻域内。在无加速收敛条件下，机械臂系统连杆1跟踪误差和连杆2跟踪误差的数值在第25次迭代时减少到零。结果表明，无需重置条件的PD型加速迭代学习控制方法对加速收敛的效果十分明显。

(2)外部干扰为随机函数。外部干扰为：d1(t)=random(1)sin(100kπt),d2(t)=random(1)×sin(100kπt)。

仿真参数：KE=0.5，kD=diag{0.45,0.45},kP=diag{6,6}。

图6和图7分别为连杆1和连杆2在第20次迭代时，跟踪轨迹曲线图。实线为期望轨迹曲线，虚线为第20次迭代时实时轨迹曲线。从图6和图7中可以得出，具有随机函数形式外部干扰的机械臂系统，在经过20次迭代后每个输出轨迹能完全跟踪其相应的期望轨迹。

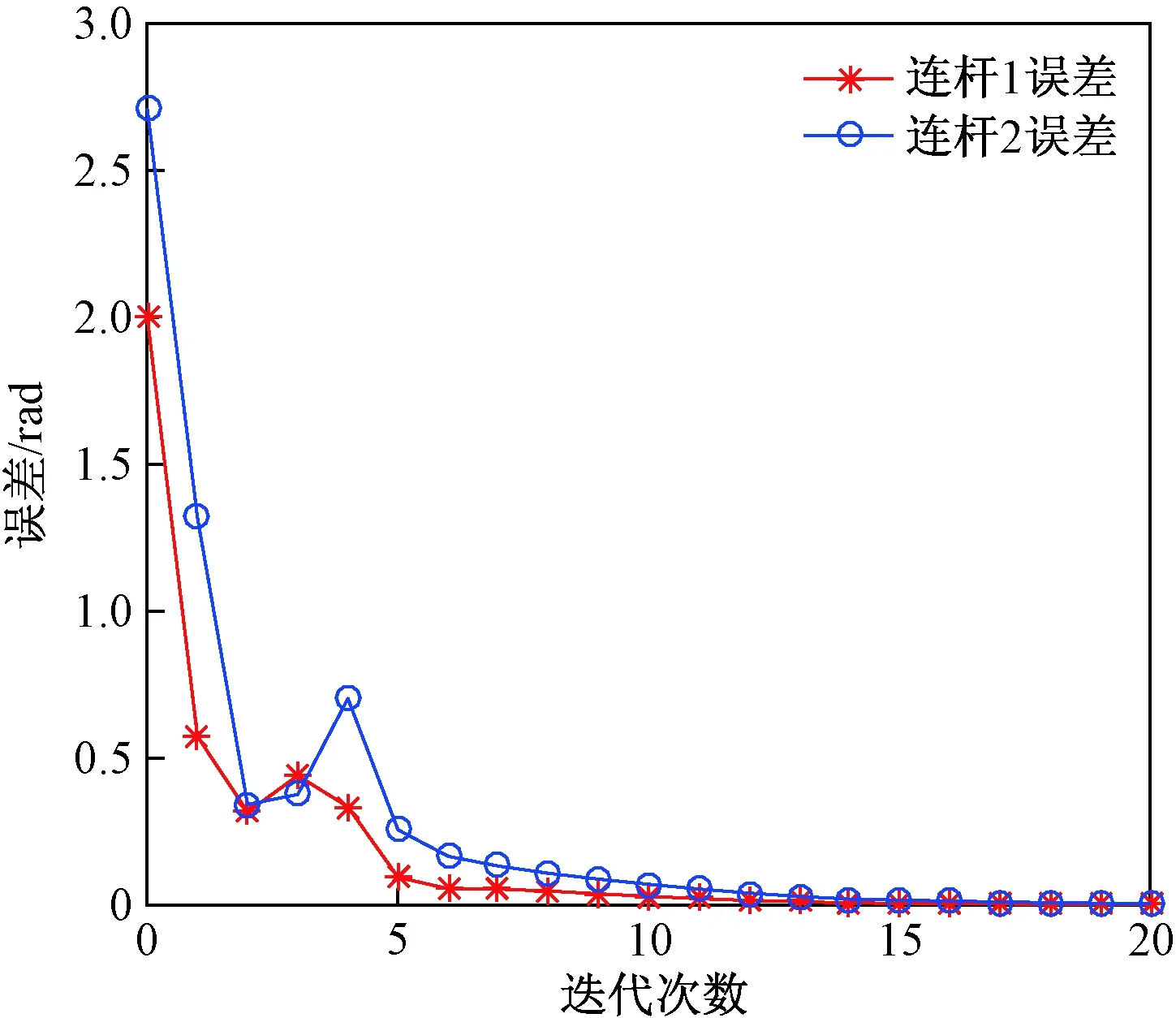
图4 跟踪误差随迭代学习次数变化曲线(正弦函数)Fig.4 The changes of tracking errors in iterations (sine function)

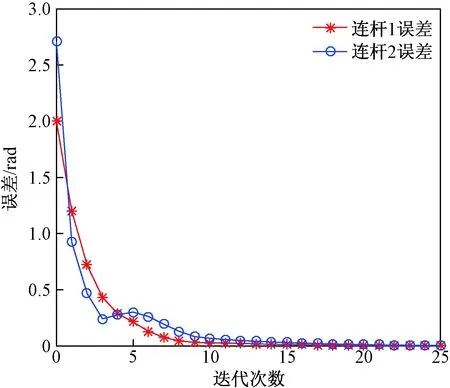
图5 在无加速条件下，跟踪误差随迭代学习次数变化曲线(正弦函数)Fig.5 The changes of tracking errors in iterations without accelerated convergence (sine function)

图8为2-DOFs机械臂系统基于无需重置条件下跟踪误差随迭代学习次数变化的曲线图，带星号为连杆1跟踪误差数值的变化图，带圆圈为连杆2跟踪误差数值的变化图。可以得出在经过16次迭代后可以完全跟踪上期望轨迹，证明无需重置条件下加速迭代学习控制算法的收敛性。为了便于比较分析，在相同仿真条件下，图9为系统在无加速收敛条件下，跟踪误差数值变化曲线图。通过对比图8和图9，可以得出跟踪误差在加速收敛算法下比无加速收敛情况下更快地收敛到零。结果表明，无需重置条件的PD型加速迭代学习控制方法对加速收敛的效果十分明显。

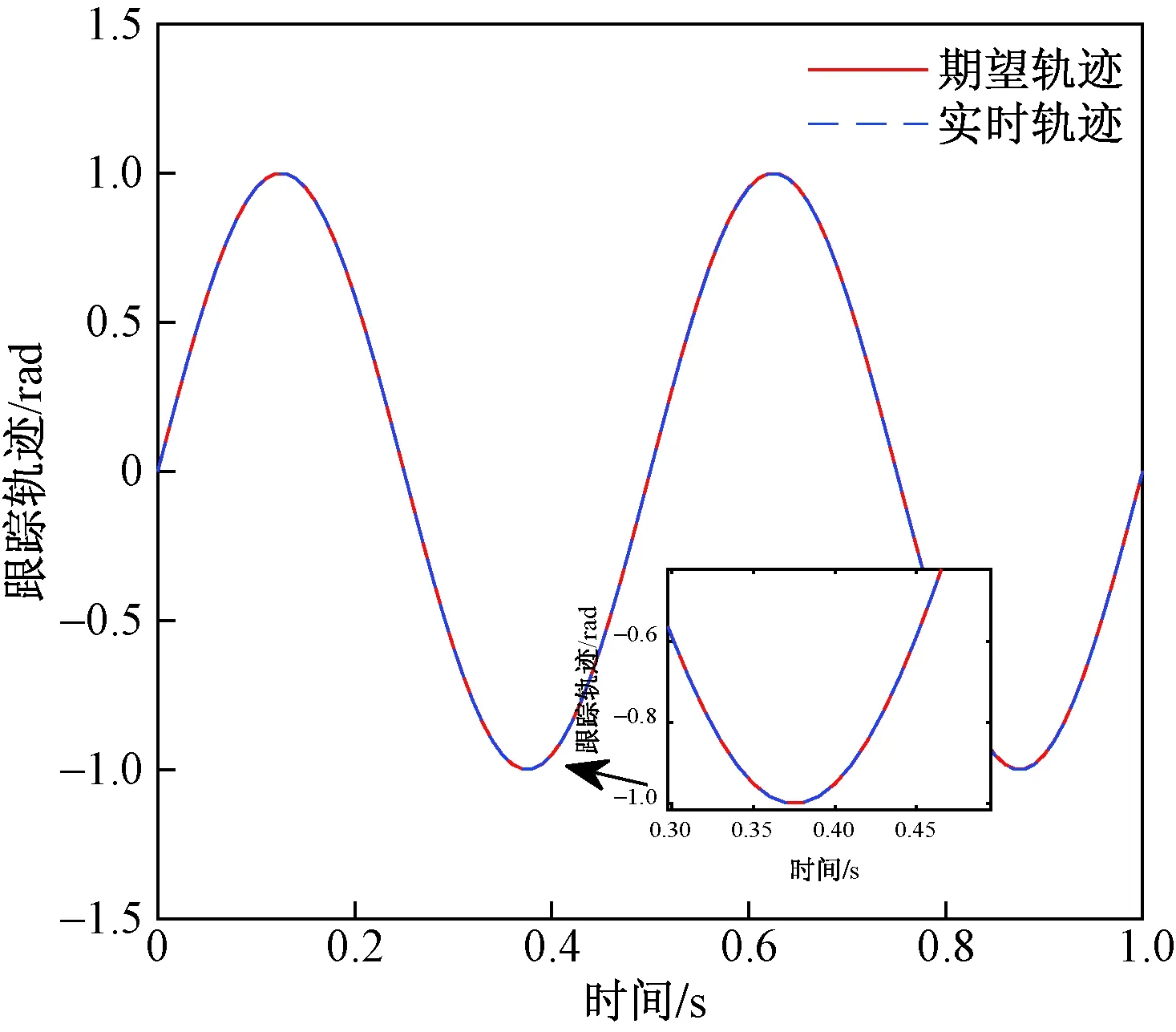
图6 连杆1的跟踪曲线(随机函数)Fig.6 Trajectory tracking of connecting rod 1 (random function)

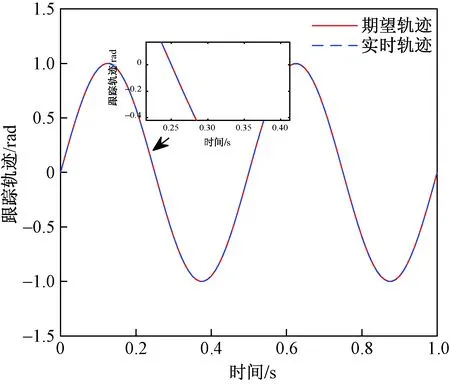
图7 连杆2的跟踪曲线(随机函数)Fig.7 Trajectory tracking of connecting rod 2 (random function)

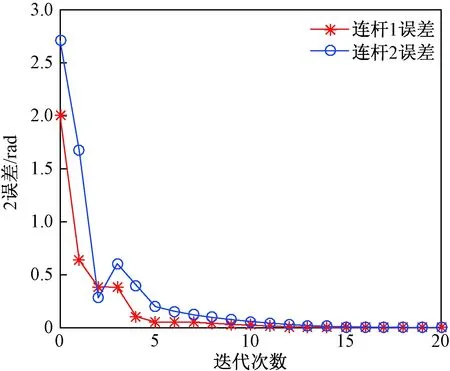
图8 跟踪误差随迭代学习次数变化曲线(随机函数)Fig.8 The changes of tracking errors in iterations (random function)

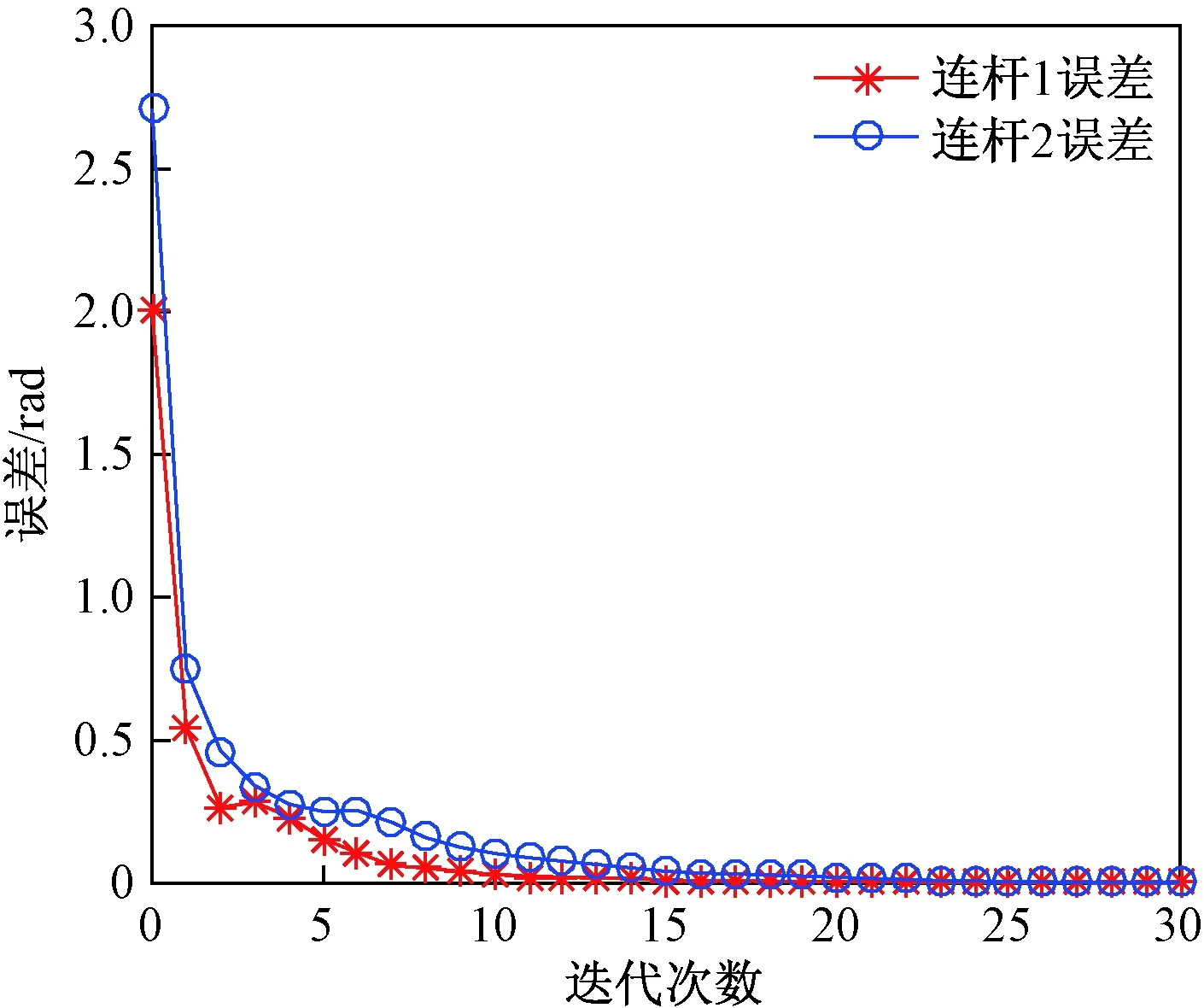
图9 在无加速条件下，跟踪误差随迭代学习次数变化曲线(随机函数)Fig.9 The changes of tracking errors in iterations without accelerated convergence (random function)

为进一步说明本文提出的无需重置初始条件下加速收敛算法的实用性，将该算法在Quanser机电一体化运动控制实验平台上运行，实验平台如图10所示。

图10 Quanser 机电一体化运动控制实验平台Fig.10 Quanser mechatronics motion control experimental platform

该实验在外部干扰为正弦函数情况下进行，外部干扰为d1(t)=sin(30kπt)，d2(t)=sin(30kπt)。

仿真参数：KE=0.1,kD=diag{0.75,0.75}，kP=diag{5,5}。

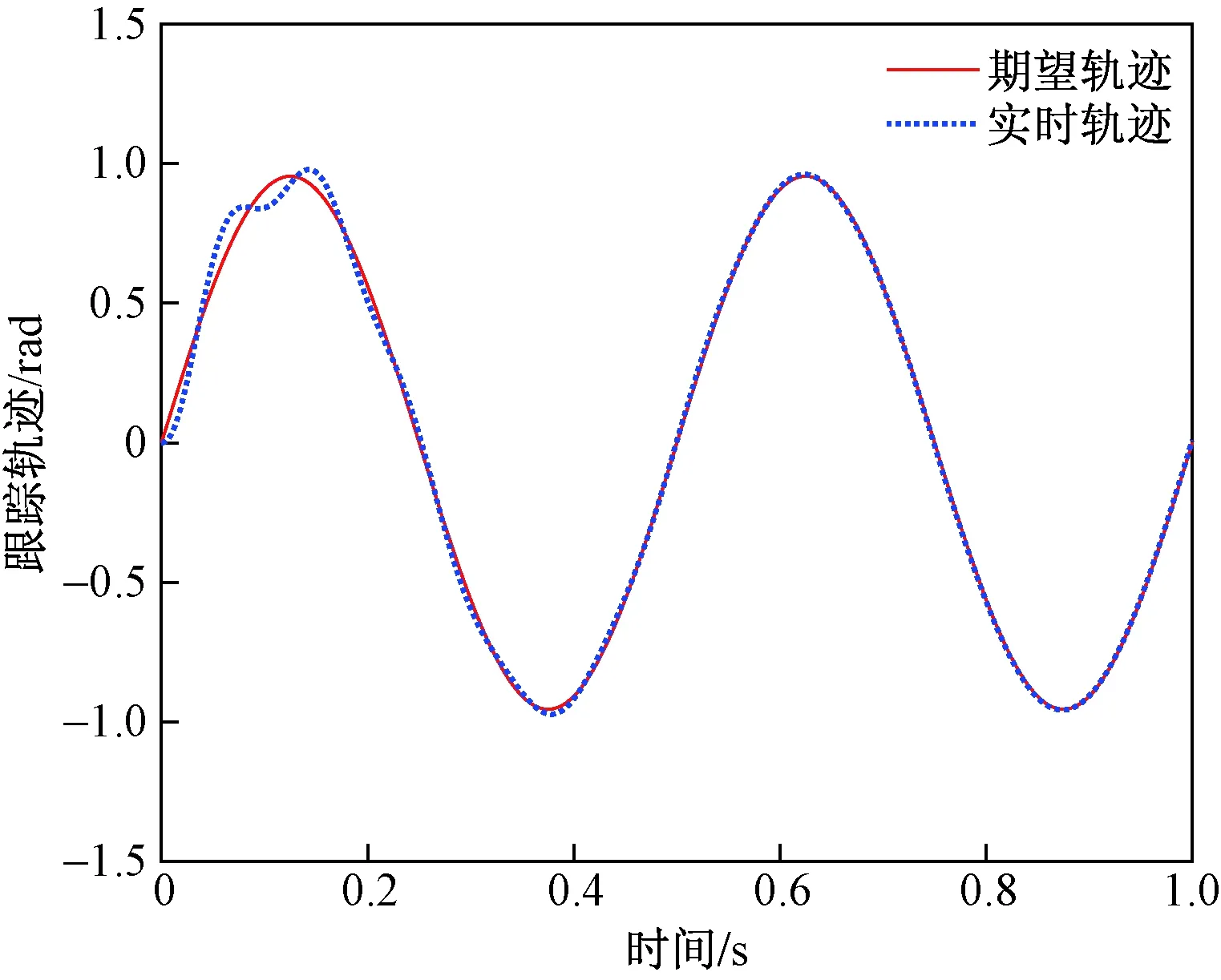
图11 连杆1的跟踪曲线Fig.11 Trajectory tracking of connecting rod 1

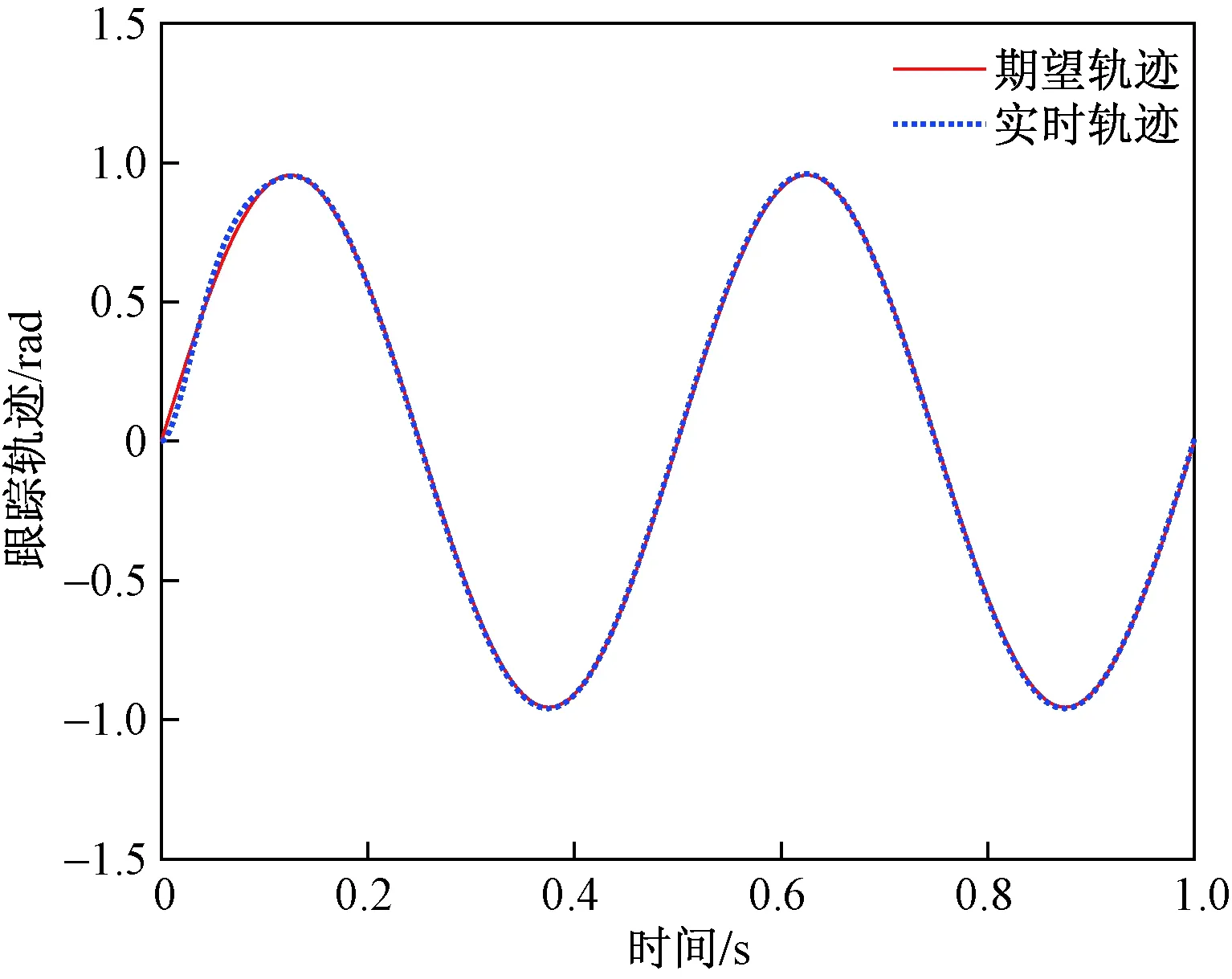
图12 连杆2的跟踪曲线Fig.12 Trajectory tracking of connecting rod 2

图11和图12分别为机械臂系统连杆1和连杆2经过20次迭代后曲线图。实线为期望轨迹曲线，虚线为第20次迭代后实时轨迹曲线。从图11和图12中可以得出，在前0.2 s内存跟踪轨迹不能完全跟踪上期望轨迹，在0.2 s后机械臂的每个输出轨迹在Quanser机电一体化运动控制实验平台上，利用无需重置条件加速迭代学习控制算法，经过20次迭代后能完全跟踪其相应的期望轨迹。说明本文提出的算法的实用性。

4 结论

针对存在不确定性的2-DOFs机械臂系统，提出了一类无需重置条件的PD型加速迭代学习控制方法。首先，利用指数变增益加速学习控制律。基于ILC算法，无需重置每次运行时的初始条件。其次，在λ范数意义下，证明了无需重置条件的PD型加速迭代学习控制算法的收敛性。最后，通过对比仿真实验表明无需重置条件下加速迭代学习控制算法能够有效加速收敛，并将该算法在Quanser机电一体化运动控制实验平台上进行验证，进一步说明本文提出算法的实用性。因此，本文提出的无需重置条件PD型加速迭代学习控制算法是可行有效的。