具有输入量化的信息物理系统的安全控制

贾欣婷, 郑柏超,2*, 刘晓光, 贾忠益

(1.南京信息工程大学自动化学院， 南京 210044； 2.江苏省大气环境与装备技术协同创新中心， 南京 210044；3.海军大连舰艇学院航海系， 大连 116018)

信息物理系统(cyber-physical systems, CPS)是一种信息系统和物理系统的融合体，具体是一个通过实时感知物理系统状态，而后在信息系统内通过模型分析形成对物理系统的调控策略，再对物理系统执行调控的循环迭代过程[1]。与传统的控制系统相比，信息物理系统具有低成本、 低功耗、安装和维护简便以及易于实现远程控制等优点。因此，信息物理系统在制造业、航空航天、交通运输、民用基础设施、医疗保健、智能电网等领域得到广泛应用[2-5]。同时，随着信息技术的不断发展，网络安全方面的问题[6-9]成为了当下的一个热点。

从信息物理系统的安全性考虑，由于信息物理系统使用开放的通信设备，攻击者可以通过访问网络层并篡改系统测量和控制输入数据，从而严重影响系统的性能和完整性[10]。由于恶意攻击者的阴谋可能导致攻击信号无法检测到，因此，在针对执行器攻击的信息物理系统的弹性和可靠控制问题中，文献[11]提出了一种基于事件触发的安全观测器控制策略。在文献[12]中，提出了自适应控制体系结构来缓解信息物理系统中的传感器攻击以恢复系统性能。在文献[13]中，同时考虑传感器和执行器攻击，提出了自适应控制策略以确保系统的稳定性。在文献[14]中，提出了针对频率约束的传感器和执行器在无报警情况下攻击的相应弹性控制方法。

另外，由于将网络嵌入到实时控制回路之中，数字通信在现代工业控制系统中的广泛应用，不可避免地引入了信道带宽限制的问题，如数字网络传送信号的量化误差。对于网络系统量化反馈控制问题，已经有不少信号量化领域的成果发表，信号量化的过程可以看作是编码和解码的过程，在文献[15]中，针对具有输入量化和外部扰动的不确定线性系统，设计了状态反馈控制器。然而该方法未考虑实践中可能导致量化编码/解码参数不匹配的问题。针对此缺陷，文献[16]研究了具有量化参数不匹配的线性系统的控制器的设计。以上文献都是将通信网络中的网络攻击和信号量化独立进行研究的，所以在这些通信约束的基础上，如何对信息物理系统进行稳定性分析与控制器设计，是当前的研究重点。

现针对信息物理系统，研究其在执行器攻击、外部干扰和量化编码器/解码器参数不匹配情况下的控制器设计。鲁棒自适应控制器包括线性和非线性两部分：线性部分的增益由线性矩阵不等式给出，旨在考虑信息物理系统H2性能问题；非线性部分用于消除外部干扰、量化误差以及抑制或抵消隐蔽式假数据执行器攻击对系统的影响，以确保闭环系统的稳定。

1 预备知识及问题描述

1.1 预备知识

1.2 问题描述

CPS系统结构如图1所示。它由物理系统层，网络层以及控制层组成。物理系统、异常检测器、编码/解码器不匹配和执行器攻击的模型描述如下。

图1 信息物理系统结构图Fig.1 The structure of cyber-physical systems

1.2.1 物理系统

CPS物理系统模型由连续线性时不变的状态空间表达式形式来描述：

(1)

1.2.2 执行器攻击

执行器攻击是一种网络攻击，即虚假数据注入攻击，其主要特征是攻击者可以将错误或期望的数据注入到通过网络层传输的控制输入信号中以实现隐身和欺骗的目的，使得系统的性能受到损害。攻击的形式类似于文献[17-18]中的形式，受损的控制输入为

(2)

1.2.3 编码器/解码器不匹配

控制系统的执行过程越来越多地采用远程通信或数字方式来实现，而数字通信网络往往受到通信带宽、有限数据率等困扰，所以通常需要对所测得的信息进行量化处理。量化器Q(·)由向最接近的整数舍入的函数q(·)定义，采用如下的量化器形式：

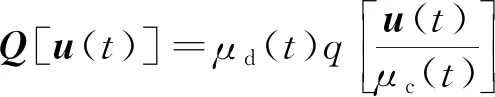
(3)

式(3)中：μc(t)和μd(t)分别为编码侧和解码侧的量化灵敏度参数，令r(t)=μd(t)/μc(t)，理想情况下μc(t)和μd(t)是相等的，即r(t)≡1。然而在实际控制工程中，由于硬件执行不理想，该要求显然是非常严格且难以实施的，所以本文考虑量化不匹配更一般的情况，

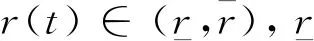
综合式(1)～式(3)，建立CPS动态方程模型为

(4)

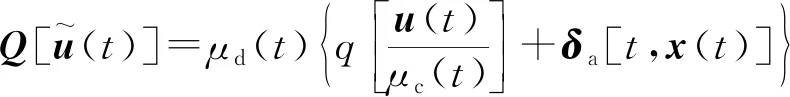
(5)

假设系统(4)配备了基于观测器的异常检测器来检查可能的异常情况。观测器形式如式(6)所示。

(6)

(7)

令g(t)=ζT(t)ζ(t)，异常检测器的检测准则为

(8)

式(8)中：Jth是阈值；H0表示系统正常运行；H1表示系统异常，检测器触发警报。

为了得到系统隐蔽式攻击的上界，令d(t)=0，式(7)变为

(9)

(10)

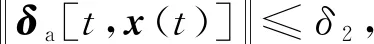
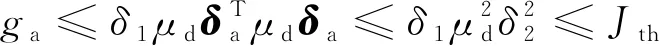
(11)

根据式(11)可以得到系统隐蔽式攻击的上界为

δ2≤J0

(12)

(13)

(14)

δ2≤J2

(15)

在给出本文的控制器设计之前，首先引入如下的性能指标的概念[12]：

(16)

式(16)中：Q和R是给定的对称正定加权矩阵；K是控制器中给出的线性反馈增益矩阵。

2 鲁棒控制器的设计

在无警报情况下，攻击也可能发生，从而降低系统性能。所以，在本文中针对上述未触发警报的信息物理系统[式(4)]，设计一种新型鲁棒控制器来消除隐蔽式攻击、量化参数不匹配以及干扰对系统的影响，从而保证闭环系统的稳定性并同时实现CPS的最佳性能J(t)。

对系统[式(4)]，设计如下的鲁棒自适应控制器:

u(t)=Kx(t)+un(t)+ua(t)

(17)

式(17)中：线性部分Kx(t)中的增益K待求，使系统实现式(16)的H2性能；un(t)与ua(t)为控制器的非线性部分，其中：

(18)

un(t)为处理量化误差和外部干扰对系统的影响，

(19)

ua(t)为抑制或抵消状态相关的执行器攻击对系统的影响；σ(t)是满足式(20)的正函数：

(20)

(21)

式(21)中：参数η为正的调节增益。

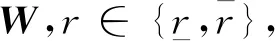
min Trace(M)

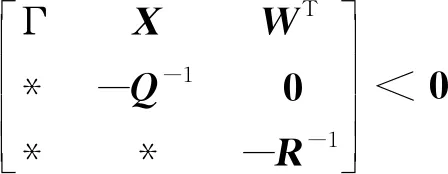
(22)

(23)

式中：Γ=AX+XAT+rBW+rWTBT，当取控制器增益矩阵K=WX-1，则由式(17)给出的满足式(18)～式(21)的控制器能使闭环系统是渐近稳定的。当δa[t,x(t)]=0时，系统满足H2性能，并可以通过最小化矩阵M的迹来达到最小的H2性能上界。

Ax(t)+rB(u+eμc)+μdBδa[t,x(t)]+Bd(t)=

Ax(t)+rB[Kx(t)+un+ua+eμc]+

μdBδa[t,x(t)]+Bd(t)

(24)

和

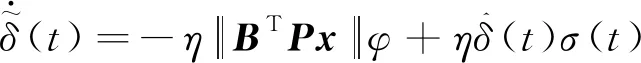
(25)

取Lyapunov函数：

(26)

对V(t)沿系统[式(24)]关于时间t求导得：

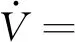
xT(ATP+PA+rKTBTP+rPBK)x+

2rxTPB(un+eμc+ua)+

(27)

2rxTPB(un+eμc)+2xTPBd≤2rxTPBun+

利用通分，配方等技术可得：

(28)

如果不等式

ATP+PA+rKTBTP+rPBK+Q+KTRK<0

(29)

成立，可以得到：

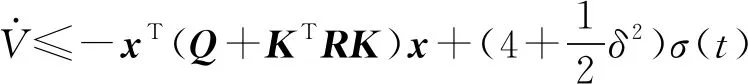
(30)

在式(30)两边同乘以P-1，令X=P-1以及W=KP-1，根据Schur补引理，可以得到如式(22)的不等式。

(31)

对式(30)两边进行时间[t0,t]上积分，得：

(32)

进一步，结合式(31)和式(32)可以得到：

(33)

因此，ξ(t)是一致有界的，意味着x(t)也是一致有界的，所以x(t)是一致连续的。根据式(32)以及V[ξ(t)]≥0，可得：

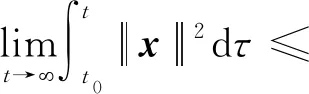
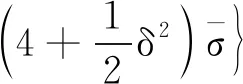
(34)

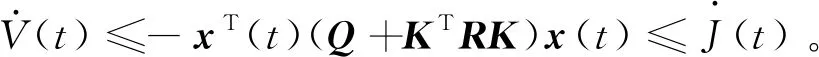
从上述结论可以看出系统H2性能的上界与系统的初始状态x(0)有关，而在实际应用中，很难精确确定系统的初始状态，为了克服这一困难，可以假定初始状态x(0)是一个满足E{x(0)xT(0)}=I的零均值随机变量。通过考虑性能指标的期望值，得到

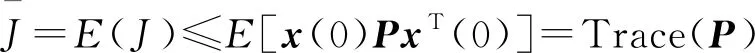
(35)

所以，系统性能的上界与矩阵P的迹有关，定理1中的约束条件[式(23)]等价于M>P>0，因此，对于δa[t,x(t)]=0的情况，可以最小化矩阵M的迹来达到最小的H2性能上界。由此定理1证明完毕。

3 数值仿真

根据定理1，选取参数矩阵Q=I2，R=0.1，利用线性矩阵不等式工具箱求解式(22)～式(23)可得：

为说明隐蔽式虚假数据注入攻击和输入量化对系统的影响以及本文算法的优越性，仿真中考虑如下三类情况。

(1)考虑隐蔽式虚假数据注入攻击的信息物理系统，仅采用线性状态反馈控制。

(2)同时考虑虚假数据注入攻击和输入量化灵敏度参数不匹配的信息物理系统，仅采用线性状态反馈控制。

(3)同时考虑虚假数据注入攻击、输入量化灵敏度参数不匹配和外部干扰的信息物理系统，采用本文提出的式(17)～式(21)鲁棒自适应控制算法。

情况① 运用MATLAB/Simulink对算例进行仿真，在线性状态反馈控制u=Kx(t)的作用下，闭环系统[式(4)]的状态轨迹和控制输入分别如图2和图3所示，异常检测器的曲线轨迹如图4所示。可以看出，当系统遭受隐蔽式虚假数据注入攻击时，检测器并未触发警报，但系统的状态和输入响应不能收敛到零，系统控制性能较差。

图2 执行器攻击下系统状态响应曲线Fig.2 Response curves of system state under actuator attack

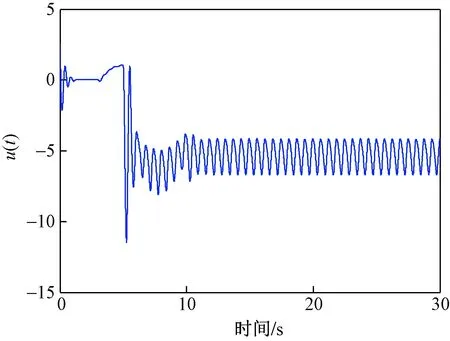
图3 执行器攻击下系统控制输入响应曲线Fig.3 Response curve of system control input under actuator attack

图4 执行器攻击下检测函数响应曲线Fig.4 Response curve of detector under actuator attack

情况② 运用MATLAB/Simulink对算例进行仿真，在线性状态反馈控制u=Kx(t)的作用下，得到系统的状态和控制输入响应曲线如图5和图6所示，与情况①的响应曲线相比，仅是区间震荡的系统状态和控制输入直接趋向于发散，呈现不稳定现象，说明输入量化灵敏度参数不匹配对系统性能的影响。

图5 执行器攻击和量化不匹配下系统状态响应曲线Fig.5 Response curves of system state under actuator attack and quantization mismatch

图6 执行器攻击和量化不匹配下系统控制输入响应曲线Fig.6 Response curve ofsystem control input under actuator attack and quantization mismatch

情况③ 为了更好地阐述本文所设计鲁棒自适应控制算法的有效性，控制器参数设为η=0.000 1，εd=5，σ(t)=0.01e-0.01t， 图7和图8给出了系统的状态和控制输入响应曲线轨迹，图9给出了异常检测器的曲线轨迹。可以看出，检测器未触发警报且趋近于稳定状态，在控制算法式(17)～式(21)作用下，即使存在隐蔽式虚假数据注入攻击、输入量化灵敏度参数不匹配以及外部干扰，系统状态和控制输入也能在一定时间内趋于零，实现系统的渐近稳定。

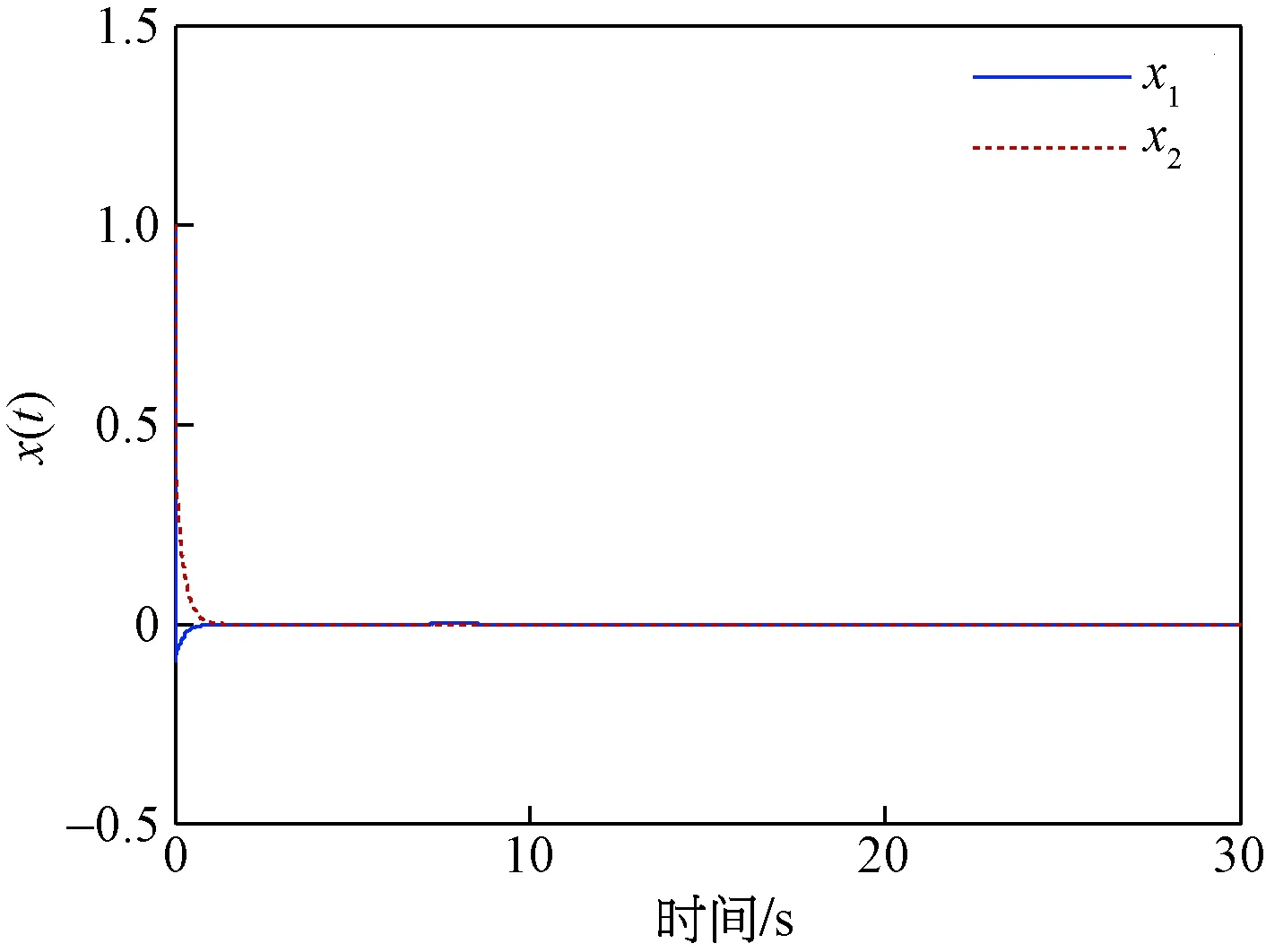
图7 本文控制算法下系统状态响应曲线Fig.7 Response curves of system state under the control algorithm

图8 本文控制算法下系统控制输入响应曲线Fig.8 Response curve ofsystem control input under the control algorithm

图9 本文控制算法下检测函数响应曲线Fig.9 Response curve of detector under the control algorithm

从上面3种情况的仿真效果对比表明，本文设计的控制算法能有效克服外部干扰、输入量化灵敏度参数不匹配、隐蔽式虚假数据注入攻击等的影响，确保信息物理系统的稳定与安全运行，充分验证了本文控制算法的有效性和优越性。

4 结论

研究了执行器攻击、量化编码器/解码器参数不匹配以及外部干扰影响的信息物理系统安全控制问题，主要做了如下工作。

(1)结合Lyapunov稳定性理论，利用线性矩阵不等式方法，分析了系统的稳定性。

(2)得到了系统满足H2性能的充分条件，给出了鲁棒自适应控制器的设计方法。

(3)与线性状态反馈控制方法相比较，所提控制策略能够有效地消除外部干扰、量化误差以及抑制或抵消状态相关的执行器攻击对系统的影响，具有较好的有效性与优越性。

下一步的工作可以对通信中断和时延等情形下的信息物理系统进行研究。