基于小世界算法的机械手时间最优运动规划
2020-12-16袁明新王丽丽庄彦武江亚峰
袁明新, 王丽丽, 谢 丰, 庄彦武, 江亚峰
(1.江苏科技大学机电与动力工程学院, 张家港 215600; 2.江苏科技大学冶金与材料工程学院, 张家港 215600)
当前,工业机器人得到了快速发展,而运动规划是机械手控制的核心和难点。基于关节空间的运动规划具有计算量低、无机构奇异和机械手冗余优点而被广泛运用[1]。孙亮等[2]采用多项式插值方法进行关节空间的运动规划,但未对此做进一步的优化;Shi等[3]提出了基于B样条插值的时间最优脉动连续轨迹规划算法,但优化复杂程度较高;赫建立等[4]提出基于遗传算法的多项式插值运动规划,但收敛速度仍有待提升。此外,上述方法都是基于多项式插值,待定参数较多,计算较为复杂。摆线运动由于提供了优异的转位特性[5],使其在工业装置如减速器[6]、凸轮[7]等中得到了广泛应用。滕举元[8]将摆线方程运用到果实采摘机械手运动规划中,体现出参数少、冲击小的优点。因此,现针对四自由度搬运机械手,结合末端分离法和摆线方程,以机械手搬运姿态、电机额定转速和额定功率为约束,建立基于时间最优的机械手关节空间运动规划模型,同时提出基于精英集聚效应的小世界优化算法来提高模型求解精度。通过数值测试结果验证文中机械手规划模型的有效性以及强规划能力。
1 机械手的关节运动学及搬运模型
1.1 机械手搬运姿态描述
基于搬运任务需要,工业生产中一些工业机器人通常设计成如图1所示的四自由度。
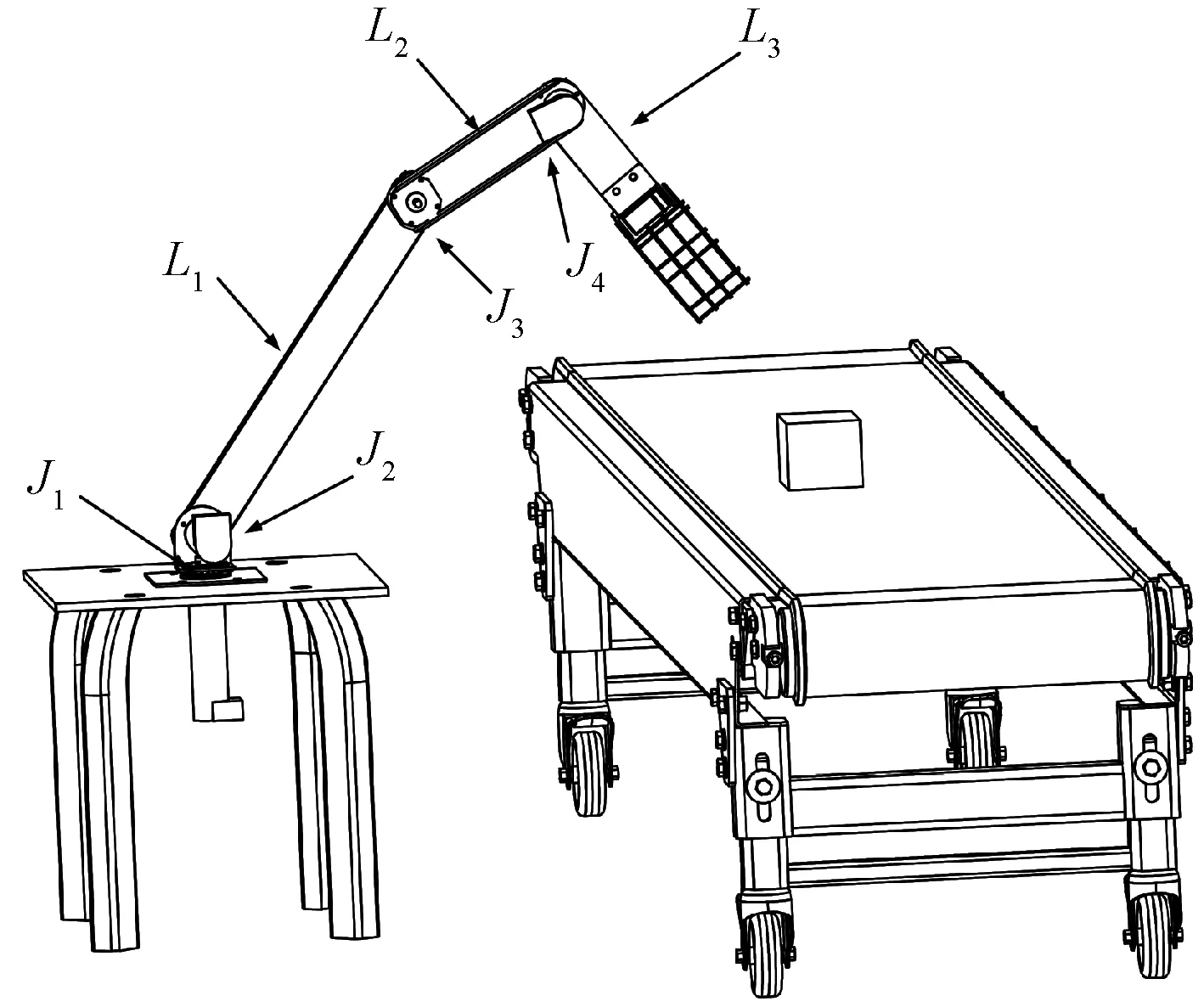
图1 四自由度搬运机械手模型Fig.1 Model of four-degree-of-freedom handling robot
图1中L1、L2、L3表示大臂、小臂、末端3根连杆;J1~J4表示4个自由度所代表的关节且分为两部分,即绕底座平面上垂线轴旋转的关节J1和位于同一平面内的关节J2、J3、J4。当J1旋转使得大臂,小臂,末端和物品点位于同一平面时,记此平面为搬运平面。在搬运平面内以J2为原点建立直角坐标系oxz,并绘制如图2所示搬运简图。

图2 搬运平面内J4边界与搬运圆Fig.2 Boundary and handling circle of the J4 in the handling plane
图2中将机械手的末端L3分离出来,包括机械手大小臂和末端执行器两部分。点划线部分是将L3绕物品中心点旋转得到的搬运圆。物品位置坐标为(x0、z0);θ1、θ2、θ3分别为L1、L2、L3与x轴正方向的夹角,其中θ3决定机械手的搬运俯仰。为避免大臂、小臂、底座间发生硬性接触,令θ1[0°, 180°]。
设L1、L2和L3的杆长分别为l1、l2和l3,建立如式(1)所示搬运坐标系解析方程。为了保证搬运解的非奇异,须使搬运处于工作空间内,即满足式(2)。上述条件成立后,可由式(3)得到θ1的极限位置,从而得到θ1的范围,记为θ1[u0,v0]。再将θ1代入式(1)可解出θ2,记为θ2=σ(θ1),其中σ()表示θ2关于θ1的函数。
(x0-l1cosθ1-l2cosθ2)2+(z0-l1sinθ1-

(1)

(2)
(x0-l1cosθ1)2+(z0-l1sinθ1)2=(l2+l3)2
(3)
1.2 摆线运动模型
物品搬运是点到点的运动,只需考虑末端到达物品处的位姿,其又可通过逆运动学转为各个关节角,故只需进行关节空间的运动规划。摆线轨迹平滑、计算简单,故可作为机械手无障碍点到点运动规划方式。摆线运动方程及其前两阶导数的正则化表达式如式(4)~式(6)所示,曲线如图3所示。

(4)
s′(τ)=1-cos(2πτ)
(5)
s″(τ)=2πsin(2πτ)
(6)
式中:τ为归一化时间。当τ=0、υ时分别表示关节运动起始时间和终止时间。
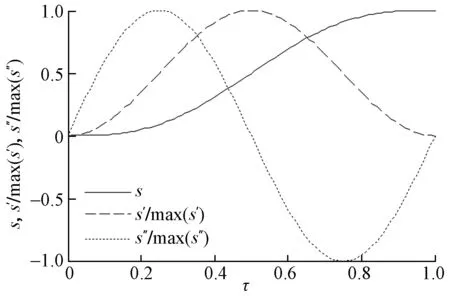
图3 摆线运动及其前两阶导数的正则曲线Fig.3 Normal curve of cycloidal motion and its first two derivatives
由图3可以看出,基于摆线运动模型下的机械手关节启动和停止都非常的稳定,无抖动发生。若已知第λ个关节的起点qλ(0)和终点qλ(υ),可以得到其运动学方程为
qλ(t)=qλ(0)+Δqλs(τ)
(7)

(8)

(9)
1.3 关节空间的运动优化模型
由于搬运平面内只有3个旋转关节,为便于公式表述,令Jλ与Lλ-1对应,λ=2、3、4。采用L1、L2、L3完全伸直并与水平面平行时的极限姿态下,计算各关节最大负载矩,如式(10)所示。再结合电机功率、转速与扭矩关系[式(11)],即可推出式(12)所示的J2、J3、J4三关节加速度公式。
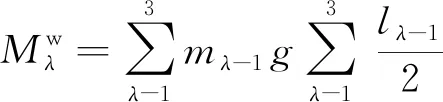
(10)

(11)
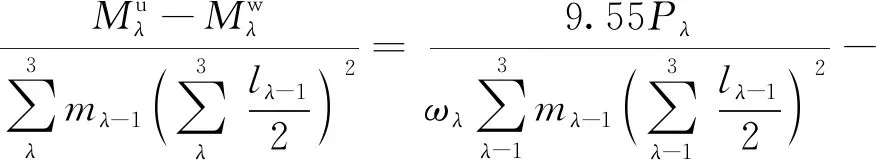

(12)
式中:mλ-1为连杆Lλ-1的质量;Pλ和ωλ分别为关节Jλ上的电机功率和电机转速;g为重力加速度。


(13)
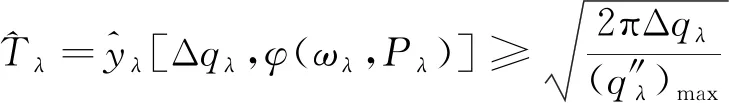
(14)
s.t.θ1[u0,v0],θ3[-45°, 45°]

(15)

以图2中坐标系逆时针为正方向,(0,l1)、(0,l1-l2)、(l3cos15°,l1-l2-l3sin15°)为J3、J4和搬运手爪的初始坐标位置,可以推出q1、q2、q3与θ1、θ2、θ3之间的关系为:q1=θ1-180、q2=180+θ2-θ1、q3=θ3-θ2-15°。以x={θ1,θ3,ωλ,Pλ}为约束变量,文中将机械手3关节运行时间最短中的长者f为优化目标,并建立优化模型。
2 基于小世界算法的机械手运动规划优化
2.1 基于精英集聚效应的小世界优化算法
小世界优化算法是借鉴美国Milgram教授所提出的“六度分离”现象,通过随机长连接和局部短连接实现优化的算法。基于精英集聚效应的小世界优化算法[9]是在此基础上,借鉴精英集聚效应将分级节点吸引策略加入随机长连接中,并根据节点优化效果进行短连接搜索次数及邻域大小的调整。数值测试结果表明,相比起其他优化算法,其优化能力、收敛速度和稳定性有了明显改善。为了提高机械手时间最优运动规划模型的求解精度,引入基于精英集聚效应的小世界优化算法(EASWA)。
2.2 机械手运动规划模型的优化
步骤1初始化算法参数:算法节点集个数n、长连接概率阈值p*、分级比例η、最大迭代次数kmax等,k← 0。
步骤2随机生成初始节点集X(0)={x1(0),x2(0), …,xn(0)}。
步骤3算法终止条件判断。当k=kmax则算法终止,并输出对应节点集X(k)。否则k=k+1,并转步骤4。
步骤4依次进行分级长连接操作Γ和自适应短连接操作Ψ。
Γ:x′ii(k)=
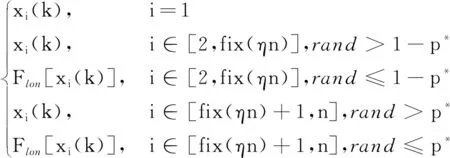
(16)
Ψ:x″ii(k)=Floc[x′ii(k)]
(17)
式中:Flon、Floc分别为个体分级长连接算子和个体自适应短连接算子,具体定义见文献[10]。
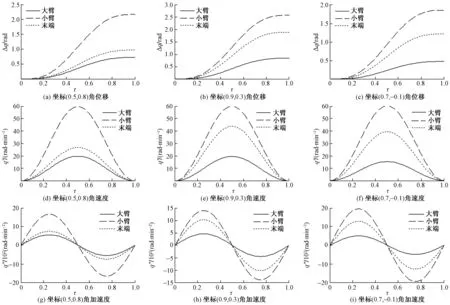
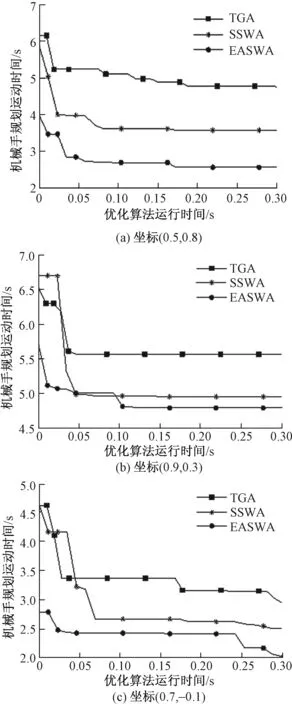
步骤5更新节点信息。i[1,n],计算f[x″ii(k)]。如果f[x″ii(k)] 图4 EASWA优化下机械手的关节规划运动曲线Fig.4 Joint planning motion curve of manipulator under EASWA optimization 表1 3种规划算法的仿真测试结果 由表1可以看出:虽然TGA平均用时最少,但是规划出的运动时间平均值以及稳定性都是3种算法里最差的。EASWA算法平均耗时虽略提高,但规划出的运动时间平均值及总均方差都是3种算法中最小的,且平均降低23.3%和19.7%,体现其强优化能力和好的稳定性。 图4为在EASWA优化下,机械手在3只货物处时间归一化的关节规划运动曲线。由图4可以看出:机械手关节运动表现较为理想,尤其大臂和小臂所对应的关节角速度基本达到额定值,说明其可以充分利用电机性能,提高机械手运行效率。图5为3种优化算法搬运运动时间的平均进化曲线。由图5可以看出,虽然SSWA优化能力强于TGA,但是其初始收敛能力相对较差,从而在有限的计算时间内无法得到较为理想的优化结果。相比之下,EASWA由于采取精英集聚效应的长连接策略,使得初始迭代就表现出很强的收敛能力;而加入自适应短连接策略,提高了搜索效率,使得算法依然能在有限时间内获得较为满意的优化性能,满足实时性要求。这也进一步验证了该规划模型的有效性。 图5 3种优化算法搬运运动时间的平均进化曲线Fig.5 Average evolution curve of handling time of three optimization algorithms 针对机械手的运动规划问题,结合机械手末端分离法和摆线方程,建立了时间最优的关节空间运动规划模型,并基于精英集聚效应的小世界算法实现了优化。通过数值测试及分析可以得出如下结论: (1)通过简化机械手结构和运用末端分离法,可以更加方便地确立搬运姿态。 (2)摆线方程具有运动平稳、参数少的优点,因此建立的关节运动时间最优模型处理较为方便。 机械手运动规划仿真测试表明,基于精英集聚效应的小世界优化算法具有较好的优化能力及稳定性,从而可以提高机械手的搬运效率。3 算法的仿真测试与讨论
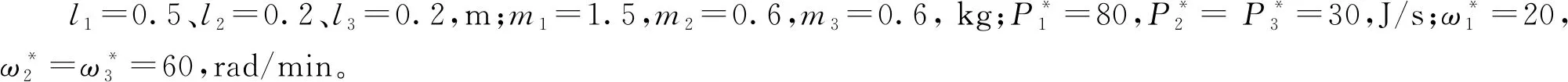

4 结论
