基于Adomian分解法的分数阶时滞Lü混沌系统的动力学分析

雷腾飞， 贺金满， 付海燕， 代文鹏

(1.齐鲁理工学院机电工程工程学院， 济南 250200； 2.南京航空航天大学航空宇航学院， 南京 210016)

1695年，德国数学家莱布尼兹给法国数学家洛必达的信中提出了分数阶的相关概念[1]。1983年，美籍法国数学Mandelbrt[2]在研究海岸线复杂边界时发现大自然中普遍存在分形的特点，分形理论的发展为分数阶得快速发展提供了支撑。从第一个混沌模型提出以后，混沌理论从动力学与时序两个方向迅速发展。近几年，根据整数阶混沌系统提了大量的分数阶混沌系统如分数阶Chen系统[3-4]、分数阶Lü系统[5]、分数阶Lorenz系统[6]等[7-11]。

对于分数阶混沌动力学系统的研究主要集中于基本动力学分析与同步控制研究，如文献[10]采用复频域法(FDM)即采用拉氏变换的基本原理，将分数阶混沌系统近似转化为高维(高阶)整数阶混沌系统，此类方法因拉式变化在转化时，考虑误差以及频率的范围，从而使得误差较大，文献[10]对分数阶Lorenz系统进行了非线性动力学的基本分析，得出分数阶不同下系统的分叉图与Lyapunov指数谱，并采用链式分数阶模块电路实现模系统的相图，电路实现结果与数值仿真结果基本一致；Adomian(ADM)分解法，对非线性项进行分解，同时通过MATLAB仿真对分解项进行迭代仿真，文献[11-12]分别采用ADM对分数阶Lü以及简化的分数阶Lorenz混沌系统的动力学进行了分析，也采用数字处理器(DSP)实现了ADM算法，为分数阶混沌系统应用于图像、语音或信号加密提供了新的思路；文献[4]采用经典的预估-矫正法对分数阶Chen混沌系统进行求解与同步控制，同时设计分数阶混沌系统的同步控制电路，电路仿真结果验证同步控制算的可实现性；上述文献均是针对无时滞的分数阶非线性系统进行分析与控制的相关研究，而未考虑实际工程系统中的时滞因素。如文献[13]分析了时滞对于悬架系统的影响，并采用LQG-Pade逼近合拍对时滞因素进行了改善；文献[14]针对不确定非线性时滞大系统，提出了基于时滞代换的自适应分散容错控制。对于非线性系统，时滞项的加入，都增加系统复杂度，时滞系统可作为高维系统处理，而对于分数阶时滞混沌系统系统的研究较少，特别是动力学行为的分析。如文献[15]对分数阶时滞混沌系统进行了同步研究,并对分数阶时滞混沌系统的混沌特性分析；文献[16]分析了具有无穷平衡点分数阶混沌系统的控制问题；文献[11-12]实现了ADM算法，该方法因运行速度快，使用资源少被广泛应用。

现以分数阶时滞Lü混沌系统为研究对象，采用ADM分解法对系统进行数值计算与仿真，得出系统相图，为了研究系统特性随参数变化的规律，运用MATLAB软件绘制0.9阶时滞Lü混沌系统的分岔图、复杂度图，以期该数值仿真结果为该系统应用于多媒体加密中的参数调节奠定基础[17]。

1 分数阶时滞Lü混沌系统

现在Lü混沌系统的基础上提出分数阶时滞Lü混沌系统：

(1)

式(1)中：x、y、z为状态变量；a、b、c为系统参数。

令系统的初始值为

(2)

则

(3)

(4)

(5)

(6)

(7)

(8)

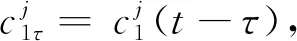
当ti≤mh时,

(9)

当ti>mh时,

(10)

式中：t为时间；τ为延迟时间；[]为取整数。

从而，得出系统的解析解为

(11)

当a=30,b=2.93,c=22.2，q=0.9,τ=0.01时，根据式(11)可得出系统的近似解，运用MATLAB对其进行数值仿真，得出式(1)的混沌吸引子如图1所示。

2 分数阶时滞Lü混沌系统分岔图与复杂度

为了进一步研究系统参数对分数阶时滞Lü混沌系统的影响，采用分岔图与系统谱熵(SE)复杂度工具，对系统的混沌特性进行研究。

2.1 参数q的变化

选取参数a=30,b=2.93,c=22.2，τ=0.01，改变q(q∈[0.65,1])，分数阶时滞Lü系统的分岔图与复杂度如图2所示。由图2可知q∈[0.65,0.66]分数阶时滞Lü系统处于发散状态，此时由于发散的原因，分岔图无法取到最高点，故分岔图在此区间出现了空白，此区域对应的复杂度也对应为最高点，无法获得；q=0.81出现了周期窗口，此区间复杂度较低，数值为0.2，复杂度于分岔图具有一致性；其他区域系统处于混沌态，系统复杂度对应的数值较高，同时，还可以看出随着系统分数阶的增大，系统复杂度减少。特别在图像加密或通信加密中，复杂度高的系统加密效果更好，故选择分数阶系统为最佳选择。

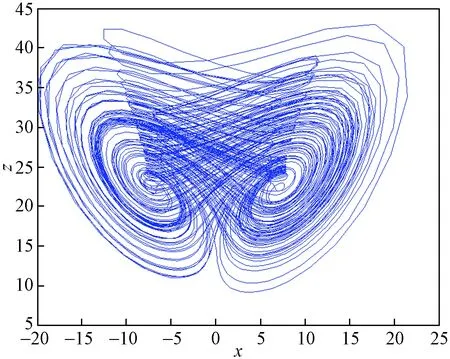
图1 系统的吸引子相图Fig.1 Phase diagram of the system

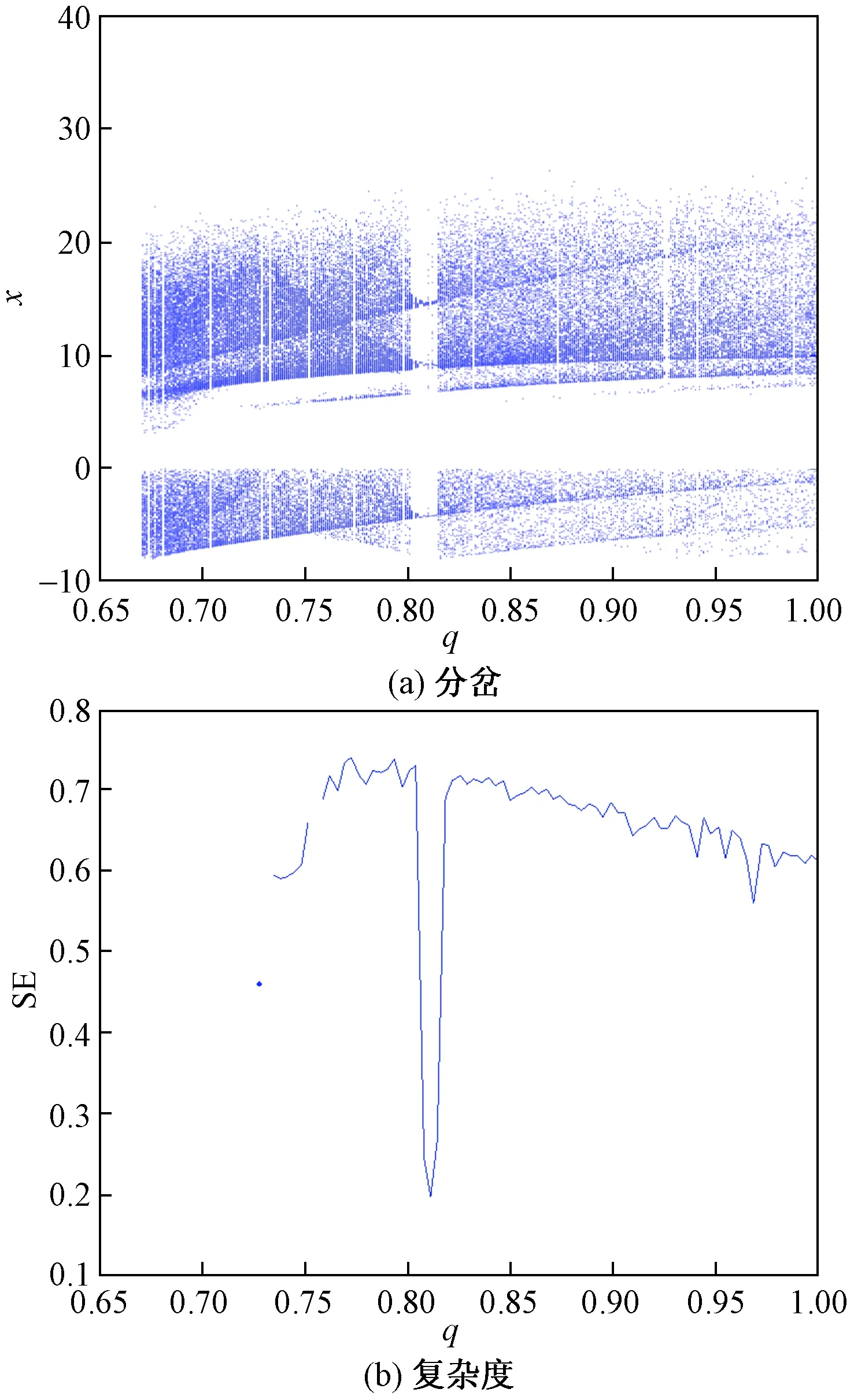
图2 q变化时系统的分岔图与复杂度Fig.2 Bifurcation diagram and complexity of system with q changes

2.2 参数a的变化

图3 a变化时系统的分岔图与复杂度Fig.3 Bifurcation diagram and complexity of system with a changes

选取参数b=2.93,c=22.2，q=0.9，τ=0.01，改变参数a(a∈[20,50])，系统的分岔图与复杂度如图3(a)和图3(b)所示。由图3(a)和图3(b)可知分数阶时滞Lü系统是标准下的倍周期(PDB)分岔的方式进入混沌区域的。从分岔图图3(a)可以看出参数a∈[20,27.83]属于周期状态，此区间SE复杂度也较小，如图3(b)所示。系统的分岔图与复杂度句具有高度的一致性；a∈[27.84,47]系统属于混沌状态，此时系统的SE复杂度都处于0.7左右，相对较高。当a∈(38,39]，系统处于周期状态。

其他参数不变，改变参数τ=0.02，a∈[20,50]系统的分岔图与复杂度如图3(c)和图3(d)所示。由图3(c)和图3(d)可知时滞下分数阶Lü系统是同样是倍周期(PDB)分岔的方式走向混沌态的。a∈[20,29.3]属于周期，从分岔图中可以看到，当然系统此时的SE复杂度比较小；a∈(29.3,42]系统属于混沌状态，此时系统的SE复杂度都处于0.7左右；a∈(38,39]时系统同样属于非混沌态，系统复杂度基本很低。

为了验证以上的结论，给出τ=0.01下参数a变化下系统的相图(如图4所示)，和τ=0.02下参数a变化下系统的相图(如图5所示)。

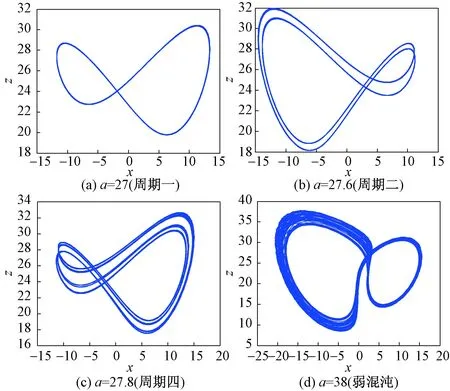
图4τ=0.01下a变化时系统的相图Fig.4 Phase diagram of the system with τ=0.01when a changing

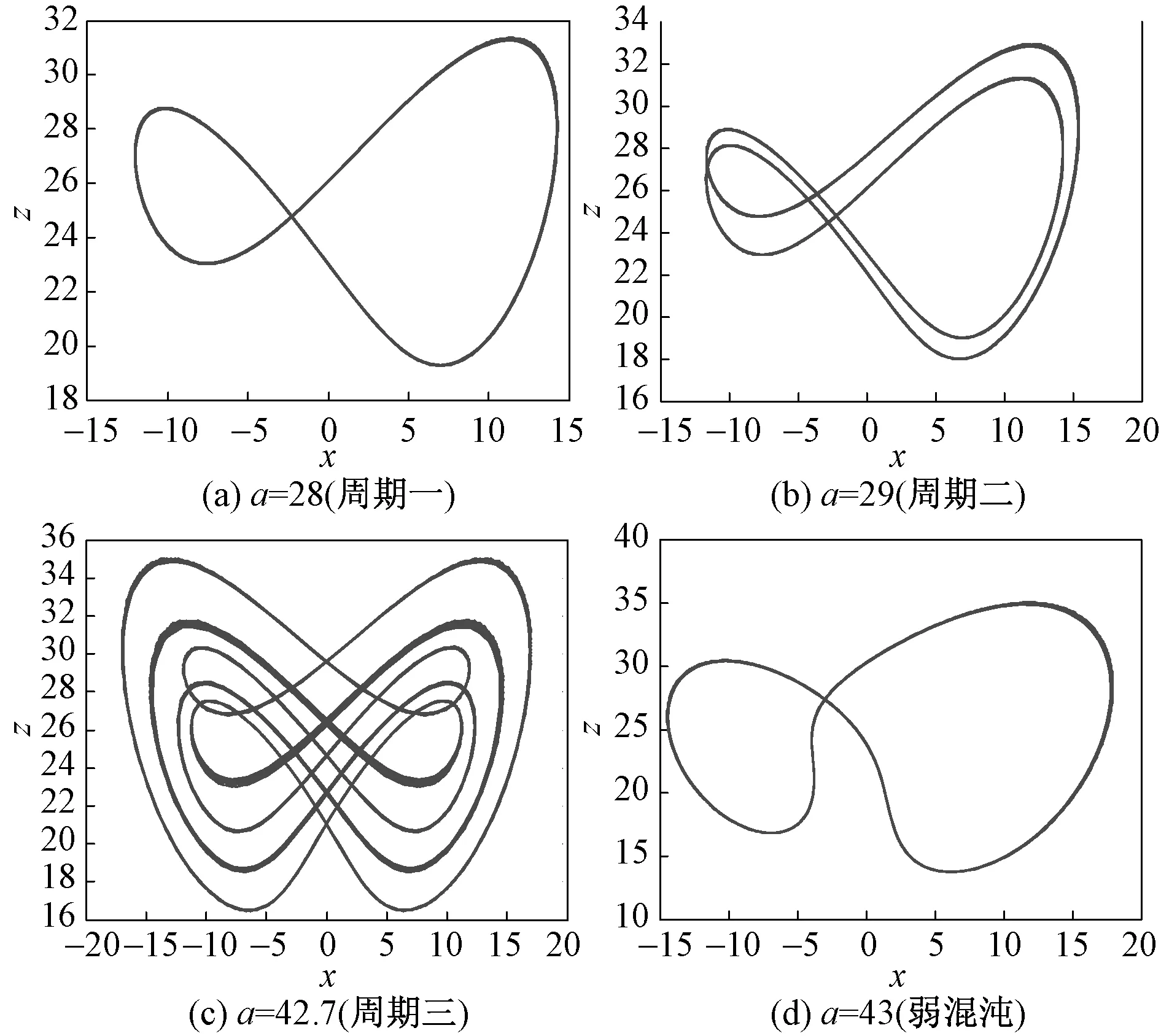
图5 τ=0.02下a变化时系统的相图Fig.5 Phase diagram of the system with τ=0.02 when a changing

2.3 参数b的变化

固定参数a=30,c=22.2，q=0.9，τ=0.01，b∈[0,4]系统的分岔图与复杂度如图6所示。b=0.1～0.2时属于周期状态，从分岔图中可以看到，系统此时的SE复杂度接近0.4左右,在此点为鞍结点分岔；b∈[0.3,4]系统属于混沌状态，此时系统的SE复杂度都处于0.6～0.7，可以看出系统分岔图与系统复杂度基本一致。对于参数b某些具体值下的系统的相图如图7所示。

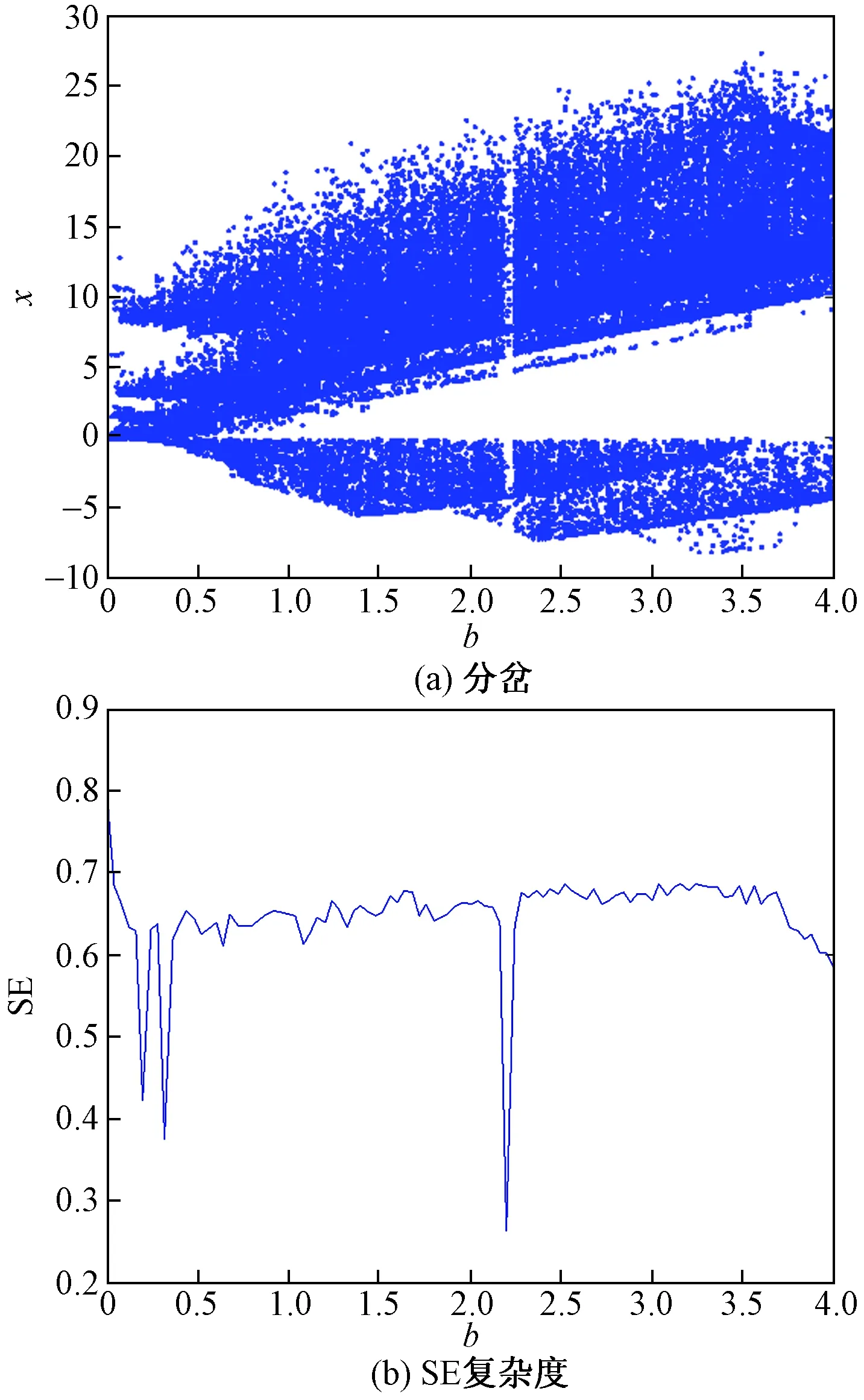
图6 b变化时系统的分岔图复杂度Fig.6 Bifurcation diagram and complexity of system with b changes

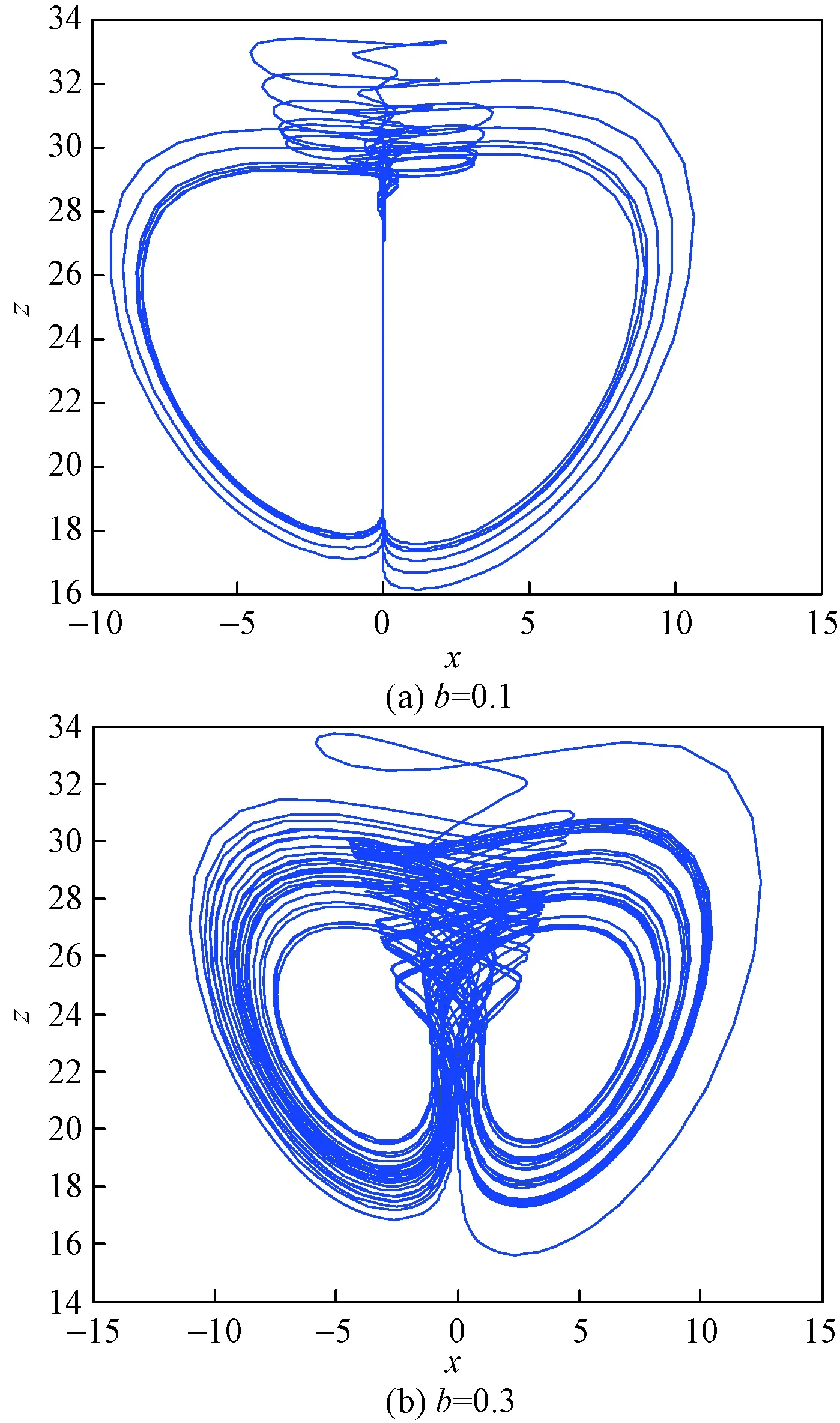
图7 b变化时系统的相图Fig.7 Phase diagram of the system when b changing

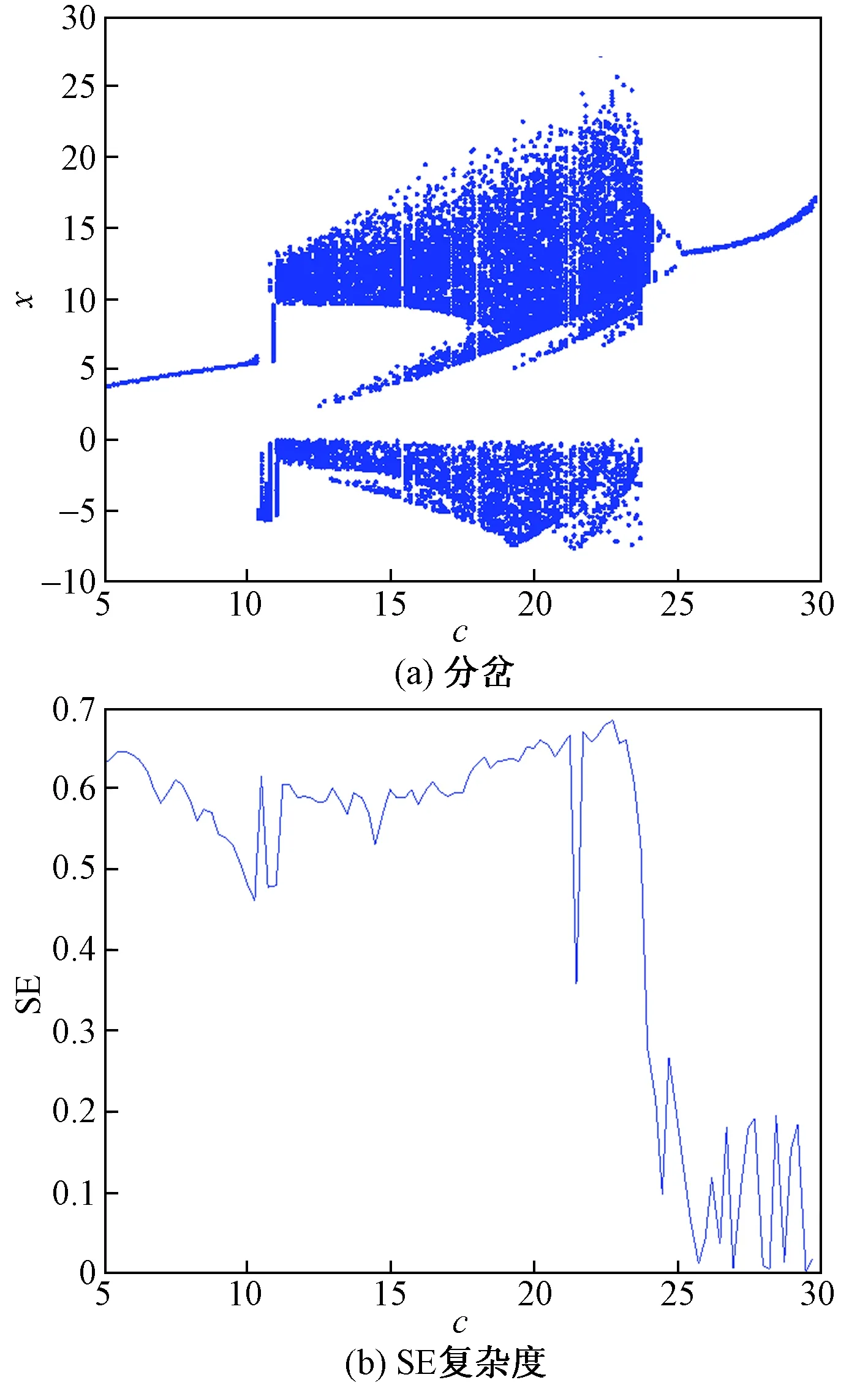
图8 c变化时系统的分岔图与复杂度Fig.8 Bifurcation diagram and complexity of system with c changes

2.4 参数c的变化

固定参数a=30,b=2.93，q=0.9，τ=0.01，c∈[5,30]系统的分岔图与复杂度如图8所示。从c减小的方向看系统是通过倍周期分岔的方式进入混沌的。c∈[24,30]属于周期状态，从分岔图中可以看到，系统此时的SE复杂度处于0.1左右；c∈[10,23]系统属于混沌状态，此时系统的SE复杂度都处于0.6左右，可以看出系统分岔图与系统复杂度基本一致。c∈[5,10)系统周期状态，此时系统的SE复杂度只是表现出下降态，并不是特别小，可以看出复杂度具有一定局限性，更对于参数c某些具体值下系统的相图，且与参数a变换时有相似之处。

3 结论

基于Adomian分解法,研究了分数阶时滞Lü混沌系统基于动力学特性。以Adomian分解法分析研究了系统吸引子、分岔图、复杂度等数值仿真分析0.9阶次时滞Lü系统的混振荡特性。同时得出分数阶时滞系统，在一定范围内随着分数阶的增大复杂度减少，从而进一步验证了研究分数阶复杂度的意义所在，分数阶系统出现混沌现象的概率大于整数阶系统。本结论为分数阶时滞Lü混沌系统的控制及其在混沌密码、数字电路等领域的应用奠定了基础。