基于ARIMA模型的河北省玉米价格预测
2020-12-16胡杨张朝阳
胡杨 张朝阳
(河北农业大学经济管理学院,河北 保定 071000)
1 研究背景
玉米是我国粮食的重要组成部分,同时也是饲料生产和农产品加工的主要原材料之一,对我国养殖业及加工业具有重大作用。玉米作为商品,具有供给需求高、价格波动程度大等特点。价格发生变化将对大量农民、养殖业和加工业从业人员的收入造成影响。价格波动较大,意味着玉米的价格会根据市场环境,供给需求量及宏观政策的调控发生变化,且变化幅度较大。本文将对玉米在不同时间段下的价格波动进行研究,建立玉米价格模型,并作出短期预测,为政府及相关企业在制定有关政策时提供科学基础。
近年来,我国在农产品价格预测方面进行了深入地研究,价格预测研究方向得到了高效且稳定发展,研究成果愈发成熟且多样。如,以农产品月度价格作为研究对象,通过向量误差修正模型深入分析了市场的价格传导情况,得到了短期市场价格之间具有长期均衡关系,这种均衡关系控制着价格很难在短时间内产生较大程度上的变化,调节了价格的偏离的结论[1];着眼于农产品价格传导,分析了农产品的价格传导情况等[2]。国内运用较多的成熟模型主要有以下几种:通过建立ARMA模型分析农产品价格波动趋势,并合理且准确的预测了以后一段较短时间内的农产品价格变化趋势[3];通过建立ARCH模型,对农产品期货价格进行分析,找寻其波动的规律,并在此基础上分析了对价格波动产生影响的因素[4];通过X-12-ARIMA季节调整模型对蔬菜价格进行实证分析,得出价格变化的主要特征为价格呈现长期稳定上升的趋势和具有季节性以及周期性波动的结论,并运用协方差分析了对蔬菜价格波动产生影响的各个因素[5];通过APSO-AVR模型对农产品价格进行了分析及预测,表明了农产品价格在较短时期内的变化趋势,同时证明了APSO-AVR模型能够较为准确地对未来价格变动进行预测,精度较高[6,7];通过EMD-AVR模型对农产品价格进行预测,结果证明该模型拟合程度较好,具有较高准确性[8,9];通过灰色预测GM(1,1)模型,将农产品价格进行模拟,以此验证该模型的预测能力[10];使用ARIMA模型对价格进行了短期预测,充分研究了该模型在对农产品价格的预测上的准确度和优越性,可根据预测结果为决策提供理论依据及现实依据[11-13];运用各种组合模型对农产品价格进行预测,得出了组合预测模型的准确度相较于单一预测模型普遍更好,能够更加准确且合理地对农产品价格进行预测[14]。
2 资料来源与统计方法
2.1 数据来源
本文所使用的河北省玉米价格数据来源于中国畜牧业信息网2011年8月—2020年11月河北省14%水分的玉米价格数据。
2.2 统计方法
本文选取ARIMA模型对河北省玉米价格进行预测,该模型是近年来最适合对价格进行短期预测的模型之一。ARIMA(p,d,q)为该模型的标准式,其中的p指代的是AR的阶数、q指代的是MA的阶数、d指代的是价格数列通过平稳性检验时进行差分的次数。
ARIMA模型分析流程如下:通过对河北省玉米价格进行初步观察,并作线型图简单判断该价格序列是否平稳;无法判断时对原始价格数列进行ADF检验,根据所得结果确定该价格数列是否平稳;如果原始序列不平稳,则将原始时间序列进行差分,并对差分后的时间序列进行ADF检验,直到成功通过ADF检验得到平稳的序列;通过AIC和SC确定模型的滞后阶数,对模型进行定阶,并对所建立的模型进行检验,根据验证其拟合优度,确定其是否可行;接着进行残差检验,确定模型是否存在自相关性;最后模型通过检验后,根据所建立的模型来对河北省玉米价格进行短期的预测和分析。
3 ARIMA模型的构建与应用
3.1 模型原理
该模型是通过扩展ARMA模型得到的更科学且符合价格变化的模型。其中含有AR模型,MA模型和ARMA模型3类。
将自回归模型称之为AR(p),表达公式:
yt=λ1yt-1+λ2yt-2+…+λpyt-p+ut
式中,λ1、λ2、…、λp为自回归相关数;ut为无法找到相关规律的白噪声;yt为p个滞后变量加权之后所得的和与白噪声相加得到的p阶自回归变量。
将移动平均模型称之为MA(q),表达公式:
yt=ut+θ1ut-1+θ2ut-2+…+θqut-q=(1+θ1L+θ2L2+…+θqLq)ut=L)ut
式中,θ1、θ2、…、θq为移动平均相关数;ut为无法找到相关规律的白噪声;MA(q)为将q+1个白噪声和白噪声滞后项进行加权后的和。称呼MA(q)为q次移动平均计算。
将自回归移动平均模型称之为ARMA(p,q),ARMA(p,q)的定义为模型中既有自回归成分,又有移动平均成分,两者同时作用于该模型之中。模型里p为自回归成分里的相关阶数,q指代的是移动平均成分中最大的相关阶数。ARMA(p,q)的表达公式:
yt=λ1yt-1+λ2yt-2+…+λpyt-p+ut+θ1ut-1+θ2ut-2+…+θqut-q
即(1-λ1L-λ2L2-…-λpLp)yt=(1+θ1L+θ2L2+…+θqLq)ut
ARMA(p,q)模型中,AR部分决定了该模型是否平稳,若平稳,则(L)=0的全部根的绝对值>1。MA部分决定了该模型是否可逆,其中(L)=0的根的绝对值应该>1。
如果原序列是单整的非平稳数据,则将非平稳数据进行差分,直到差分至数据稳定后分别对数据进行AR(p),MA(q),ARMA(p,q)建模处理。
ARIMA(p,d,q)模型的建立,关键点在于p,d,q这3个数如何进行确定。需要针对d进行判断,方式为对所研究的价格数列进行单位根检验,依据检验结果确定是否平稳,假使没有通过单位根检验,那么将该价格数列进行差分,重新通过单位根检验判断是否平稳,在通过d次差分后得到了一个稳定的数列,那么将该模型的d定义为差分次数,而后使用平稳的差分数列建立模型。需要根据自相关函数确定p的值,跟据偏相关函数来判断q的值。
自回归移动平均过程,ARIMA(p,d,q)表达公式:
Wold分解定理表明,所有协方差的平稳程序yt,都可以用下面的公式阐述:
yt-μ-dt=ut+1ut-1+

ut=yt-E(ytyt-1,yt-2,…)
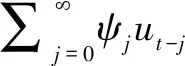
对于常见的ARMA(p,q)模型,(L)yt=+(L)ut,yt的期望:
这就是漂移项与均值的关系,所以公式也可以写为:
Φ(L)(yt-μ)=(L)ut
3.2 平稳性检验
当时间序列为平稳序列的时候,该序列的均值、方差和协方差应当在一定时间段内维持一定程度上的稳定,在该时间范围内,序列应当符合相对程度上的概率分布。而对于非平稳序列来说,如果时间序列为非平稳序列,该序列均值、方差和协方差的值会伴随时间的变化而发生变化。由此导致了非平稳序列很难通过计量经济模型分析出其内在的关系,从而难以对未来的序列进行预测。在现实情况下的分析过程中,大部分的价格序列都处于非平稳状态。所以如果所研究序列是非平稳序列,应当通过差分或取对数将该序列变成平稳序列。
本文通过ADF检验方法对数据Y进行平稳性检验,检验结果如图1所示。
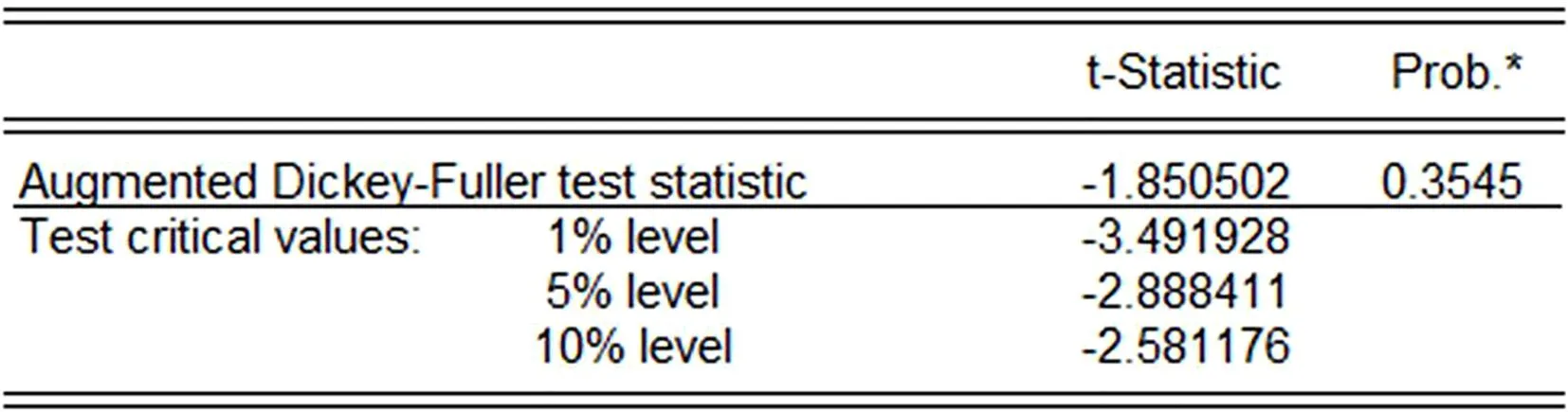
图1 Y的ADF检验结果
由ADF检验结果可知,变量Y的ADF检验统计量为-1.8505,相应的P值为0.3545,>0.05,因此在5%的显著性水平下接受原假设,即数据Y是非平稳序列,对变量Y进行一阶差分,得到变量DY,对DY再次进行平稳性检验,结果如图2所示。
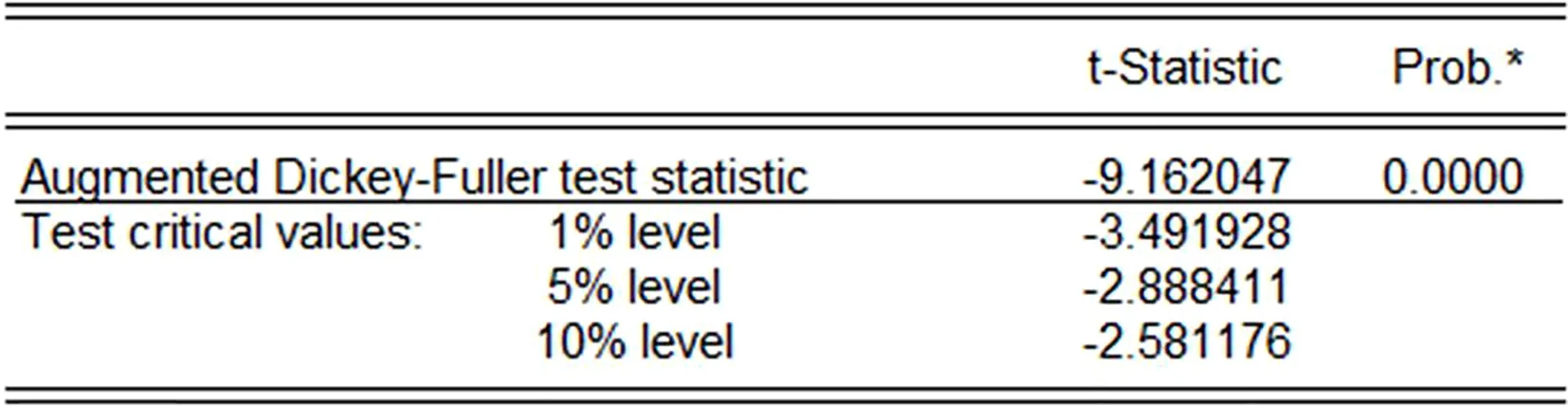
图2 DY的ADF检验结果
由ADF检验结果可知,变量DY的ADF检验统计量为-9.162,相应的P值为0.000,远<0.05,因此在5%的显著性水平下拒绝原假设,即数据DY是平稳序列,符合建立ARMA模型的平稳性条件。
ARMA模型建立本节对Y数据建立ARIMA模型。ARIMA(p,d,q)模型通过AC,PAC最小信息准则来确定阶数,本文针对常见的p,q取值,进行比较,来确定最后滞后阶数,本文通过各个模型比较可知,模型ARIMA(2,1,2)的AC值和PAC值最小,说明该模型对数据的拟合效果最好,因此本文最终确定模型为ARIMA(2,1,2)。具体模型回归结果如图3所示。
DYt=0.0019-0.5088DYt-1-0.8782DYt-2+0.5855μt-1+0.9599μt-2
T=(0.27)(-12.24)(-22.89)(28.53)(64.92)
R2=0.1004 F=2.84(P=0.0000)
由以上回归结果可知,所有回归系数在5%显著性水平下都是显著的,模型的拟合系数为0.1004,模型的F统计量为2.84,对应的P值<0.05,说明模型整体在5%显著性水平下是显著的。
3.3 残差检验
当使用针对价格数据开展时间序列研究时,必须要求所研究的价格序列可以准确地对未来进行预测,因此要求在进行预测的时候该价格时间序列中的数据必须相互关联。如果价格序列中各项价格数据间关联度极小或者没有关联性,则无法选取该价格时间序列进行分析及预测。
当所研究的序列之间无法找到相关规律,那么将该序列属于白噪声序列。原假设假定于在m期之间序列之间不具备相关性,无法从价格数据中得出准确且合理的联系,备择假设假定价格数列之间具有相关性,序列之间互相联系。对模型的残差进行自相关偏相关检验,通过检验结果对价格时间序列进行验证,从而确定该价格时间序列是否具有相关性。
模型残差检验对所构建的ARIMA(2,1,2)模型的残差进行自相关偏自相关检验,以下为针对河北省玉米价格所得模型的检验图(图4)。
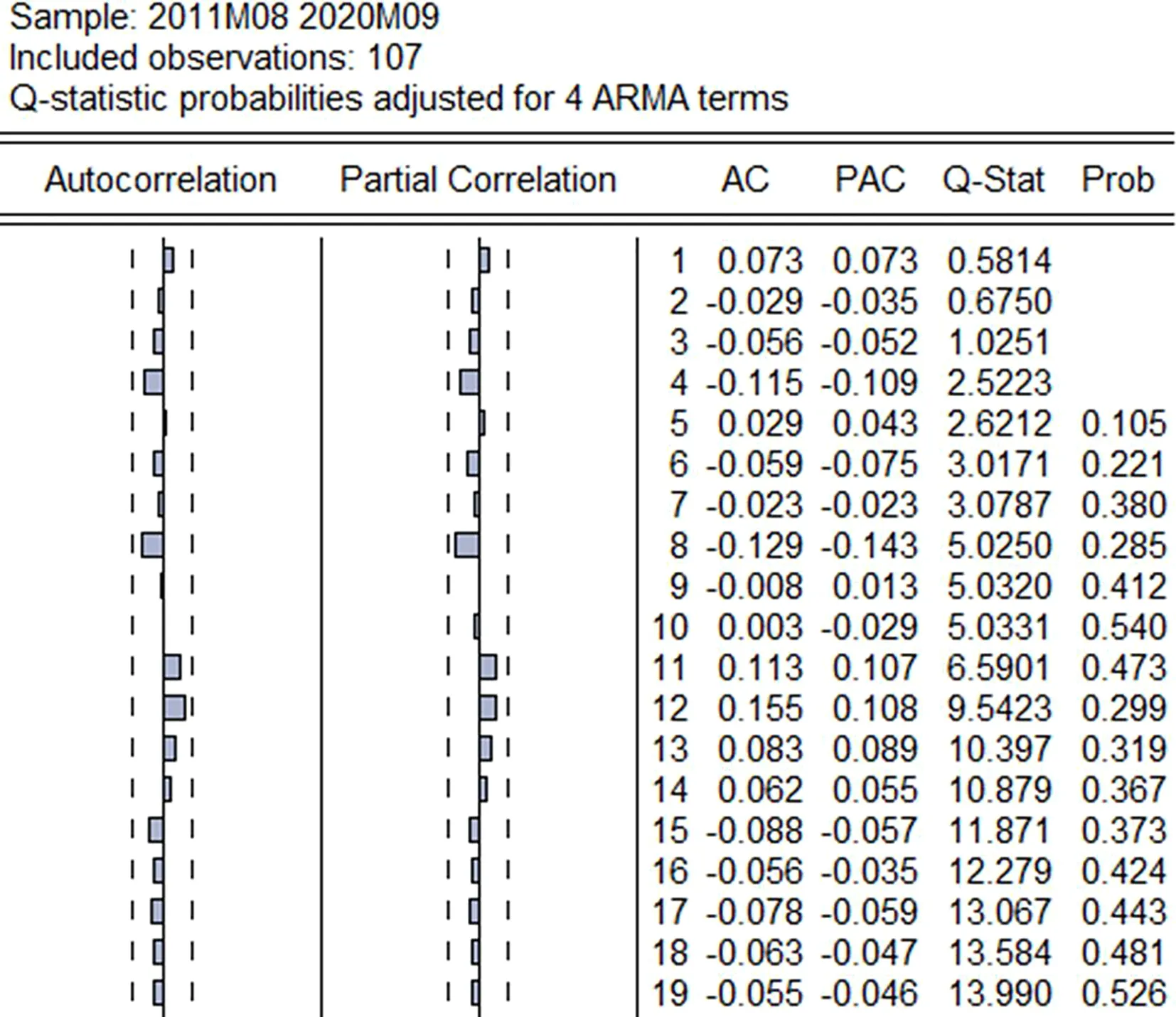
图4 自相关偏相关检验图
由以上检验结果可知,模型残差的自相关和偏自相关值全部比临界值更小,Q统计量对应的P值比0.05大,说明在5%显著性水平下,模型的残差不存在自相关性。即说明模型能够较好的刻画数据特征,模型结果较为理想。
3.4 模型预测结果
当所用数列通过检验后,根据ARIMA模型开始作出预测。由上文分析结论确定运用ARIMA(2,1,2)根据2011—2020年河北省玉米价格数据为基础来对未来价格作出预测,从而证实了所建模型ARIMA(2,1,2)具有良好的可信度。根据所得的预测(图5)进行处理分析,其真实价格处于预测的置信区间之中,这个结果证明了所建立的模型有着良好的拟合度,能够较为准确地对河北省玉米价格作出预测。
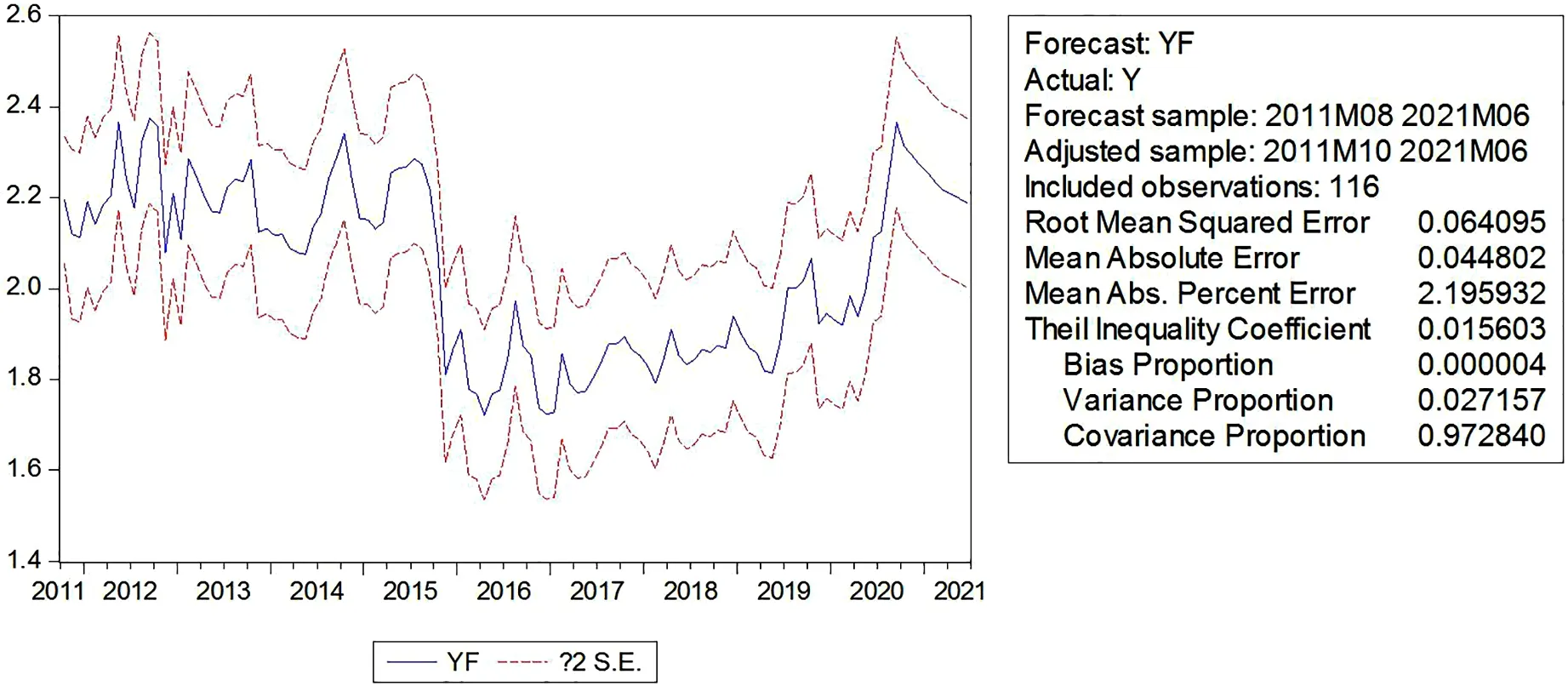
图5 模型预测结果
根据上述结果的相关数值可以从计量经济的方面对预测情况进行科学合理的表述,其中锡尔不相等系数是0.015603,其数值明显<0.05;偏相关系数的值是0.000004,该数值代表着本预测具有极高的拟合度,方差比率的数值是0.027157,以上三者都能有效证明所研究的结果具备着较高准确度。相关数值里面协方差比率的值是0.972840,其非常靠近1,出现这种结果则有力证明了该模型具有很高的可信度。但协方差比率的值很高的时候,意味着偏差极小。也就验证了预测结果同真实价格数据极其相似。
4 结论
本文用时间序列分析的ARIMA模型对河北省玉米价格变化情况进行了预测研究,建立了结构为ARIMA(2,1,2)的模型,并且用该模型对2011年8月—2020年10月的河北省玉米价格进行了分析,并预测了2020年11月—2021年6月河北省玉米价格的变化情况。模型预测结果表明2020年9—10月价格达到顶点,然后在接下来的6个月中将处于持续下行趋势。
该模型可以很好地预测河北省玉米价格变化情况。但是由于价格序列在实际分析中会随着多种影响因素的变化而变化,所以序列中的所有价格普遍具有随机性,当利用过去的真实价格数据进行预测时,不可避免地会存在一定误差,因此更适用于短期预测。应当通过不断更新数据对所建立的模型进行补充及修正,使得预测更为精确。
