高超声速飞行器快速平滑自适应二阶滑模控制

文成馀，江 驹，余朝军，朱 平

(先进飞行器导航、控制与健康管理工业和信息化部重点实验室(南京航空航天大学)，南京 210016)

高超声速飞行器突防、侦察能力强，反应时间短，飞行速度快，在军事和民用领域有着众多需求[1-2].但是由于其具有严重非线性、强耦合性、不确定性等特性，这给飞控系统的设计增加了难度，特别是在爬升段，飞行器要穿越对流层、平流层、中间层以及部分电离层，飞行速度从超声速加速到高超声速，不确定性因素[3]更多.

超螺旋滑模控制算法[4]因其具有强鲁棒性且只需要知道滑模量的信息，无需知道其一阶导数的信息等特性，已广泛应用于干扰估计[5]、极值搜索控制[6]、容错控制[7]等相关领域.文献[8]提出了一种快速超螺旋算法，通过在普通超螺旋算法中加入线性项，提高了算法的收敛速度，并基于此算法设计干扰观测器对干扰连续估计和补偿.文献[9]同样通过加入线性项来提升收敛速度，并在假设干扰上界未知的前提下，设计了一种新的自适应律，提出一种新型的快速自适应超螺旋算法.文献[10-12]通过设计一种自适应参数既可增大又可减小的自适应律，以解决参数过大估计问题.上述这些算法由于积分项中含有不连续的符号函数项，只可得到连续的控制输入曲线，控制输入不平滑，与传统一阶滑模相比，这些控制算法的确减小了抖振，但是并不能极大减小甚至消除抖振.2007年文献[13]提出一种平滑的二阶滑模控制算法，其主要思想就是在超螺旋算法的积分项中使用连续的函数，以此得到平滑的控制输入，但是这种控制方法需要非线性观测器来估计干扰，而且算法的收敛速度上还有提升的空间.

本文针对上述所存在的问题，提出一类新型的快速平滑自适应超螺旋滑模控制算法.采用滑模微分器逼近反馈线性化过程中不准确的量；控制律设计时，在普通超螺旋算法中增加线性项，并在积分项中使用连续的函数，以加快收敛速度且达到平滑控制的效果；最后，为避免参数过大估计，设计了一种自适应参数可增可减的自适应律.

1 问题描述

1.1 动力学模型

高超声速飞行器爬升段纵向动力学模型可以描述为：

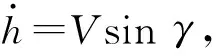
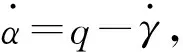
(1)

式中：M为飞行器质量；V为飞行速度；γ为航迹倾斜角；h为飞行高度；α为飞行迎角；q为俯仰角速率；Iyy为纵向转动惯量；r=R+h为飞行器地心距，其中R为地球半径；μ0=3.986×1014m3/s2为地球重力常数；g0为地表重力加速度；Isp为燃料比冲；L、D分别为飞行器升力、阻力；T为发动机推力；My为俯仰力矩；dv1、dγ、dq分别为模型不确定性、外部干扰等复合干扰.

1.2 发动机推力模型

高超声速飞行器的推力模型可简化为一个二阶模型：

式中：βc为发动机节流阀的调定值；阻尼比ζ为0.7；固有频率ωn为5.

推力系数以及燃料比冲公式为：

式中：CT为推力系数，Ma为马赫数.

1.3 空气动力与动力矩

高超声速飞行器的气动力与气动力矩可表示为：

式中：Sw为机翼浸润面积；cA为平均气动弦长；ρ为空气密度；CT、CL、CD、CMy分别为推力、升力、阻力以及俯仰力矩系数，其均与α、Ma相关，具体值详见文献[14].

1.4 控制问题

1)由于高超声速飞行器本身缺乏飞行试验数据等[15]问题，加上爬升的过程中，飞行速度、高度急剧增加，燃料大量消耗导致重心较宽范围变化等因素，将会造成模型、参数等不确定性.本文主要研究高超声速飞行器在爬升的过程中参数Sw，cA，Iy，ρ，CD,CM,CL存在摄动，且存在除参数不确定外的复合干扰时的轨迹控制问题.

2)抖振普遍存在于滑模控制中，如何削弱抖振，将其抑制到极小范围内甚至消除，一直是控制领域的热点问题.二阶超螺旋滑模将符号函数放到积分里，有效地抑制了抖振，但是并没有消除抖振.假设某系统有如下控制算法:

(2)

式中：u为控制输入;e为跟踪误差;k1、k2为控制参数.由式(2)可知，虽然符号函数通过积分，使得控制输入连续，但是不平滑，当e在0附近变化时，控制输入曲线会呈锯齿状.本文控制算法旨在既能将控制输入平滑化，又能提升收敛速度.

2 精确反馈线性化

2.1 输入/输出反馈线性化

定义向量x=[V,γ,α,β,h,M]T，将V、h分别对时间求三次和四次微分，微分表达式中将出现控制输入量，将其作为整体提取出来，可得：

(3)

2.2 滑模微分器

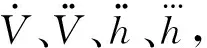
滑模微分器设计为

引理1[4,16]设f(t)=f0(t)是定义在[0,]上的函数，且有|f(n+1)|≤Sn，∀t，其中Sn为已知正常数.则在经历有限时间的瞬态过程后，有

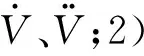
根据引理1，选择合适的参数，可以保证滑模微分器的状态量在有限时间内精确跟踪速度和高度的各阶导数.

3 快速平滑自适应二阶滑模算法

3.1 积分滑模面

定义速度和高度的跟踪误差：

eV=V-Vd，eh=h-hd，

(4)

式中Vd、hd为指令信号.

为了保证稳态跟踪精度，选择积分滑模面.根据式(3)，系统的相对阶次分别为3和4，所以设计滑模面如下：

(5)

式中λV、λh为待设计参数.

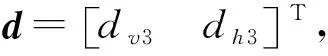
3.2 控制器结构

快速平滑自适应二阶滑模控制系统结构框图如图1所示.

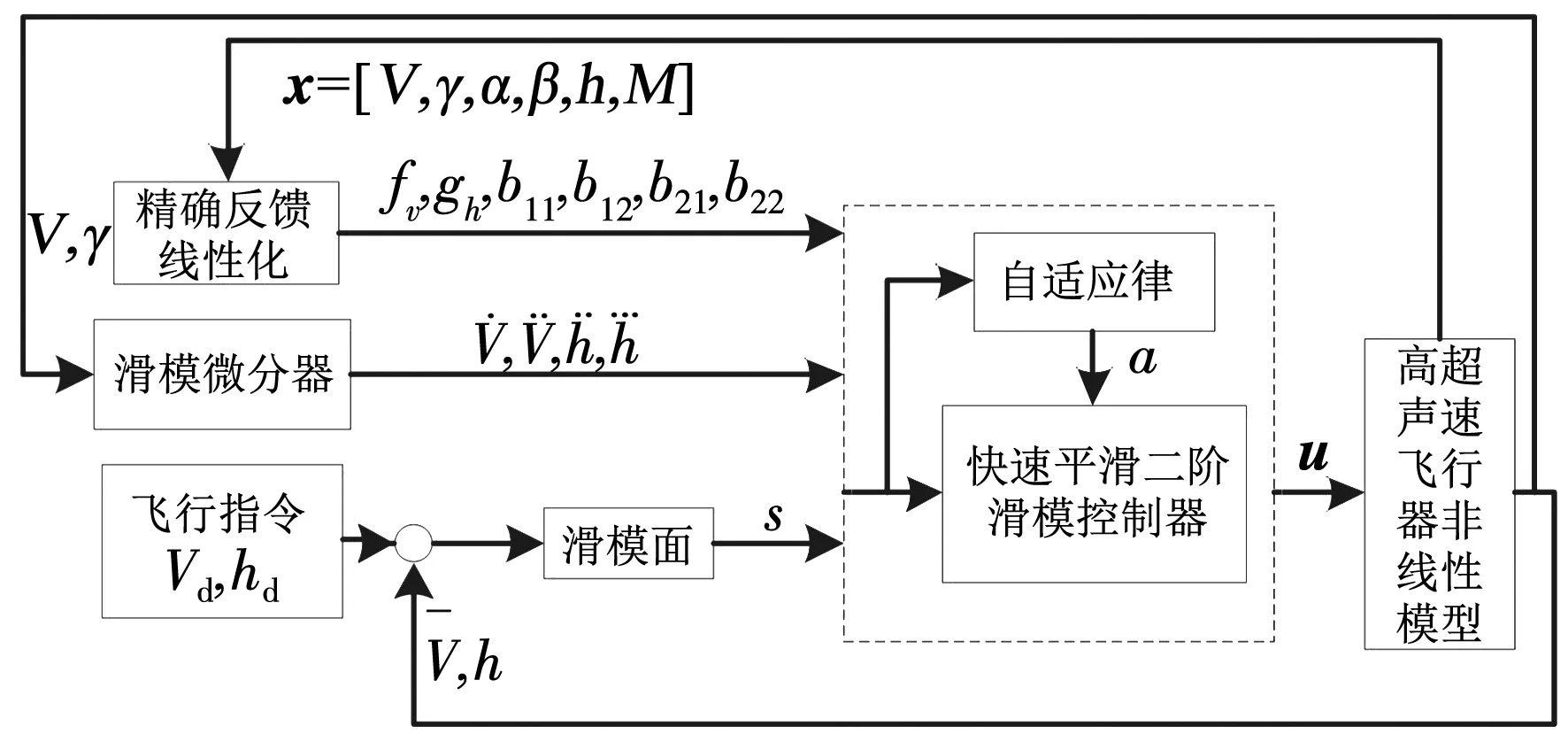
图1 总体控制结构框图

在图1中，快速平滑二阶滑模控制律可设计为：

(6)

(7)

式中：自适应律设计参数ω1,γ1>0，μ=[μ1μ2]，μ1、μ2为较小的正常数.

根据式(3)、式(4)～(6)可计算得出闭环滑模面趋近动态.鉴于滑模面sV和sh的趋近动态形式相同，下文省去下标为s，其中aVi、bVi、ahi、bhi(i=1,2)，dv3，dh3同理，可得：

(8)

情况1当m=2时，对比式(2)，该算法加入了线性项a1b2s、a2b2s，可保证|s|快速收敛到μ邻域内，但是该算法并不平滑.

情况2当m>2时，不仅可保证快速收敛，且控制输入式(6)的积分项中均是连续的函数项，故此时的控制输入是平滑的.

3.3 收敛性证明

定理1对于包含被控系统(1)、控制律(6)、自适应律(7)的闭环系统，若假设1满足，则s在有限时间内收敛于μ邻域内.

定义类二次型Lyapunov函数为

(9)

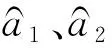
对V求一阶导:

(10)

式中：

C=[-η1-η22].

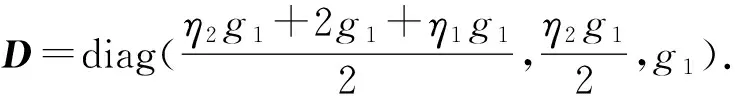
则式(10)可为

(11)

令A和B-D均为正定矩阵，可解算得：

(12)

根据：

λmin(Q)‖ζ‖2≤ζTQζ≤λmax(Q)‖ζ‖2,

(13)

(14)

(15)

式中：

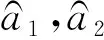
(16)

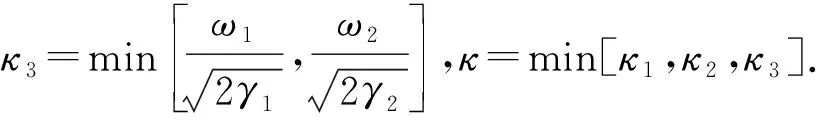
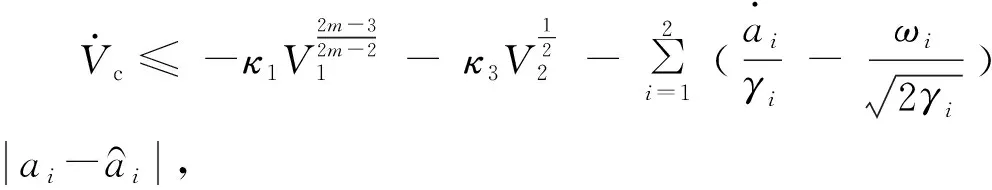
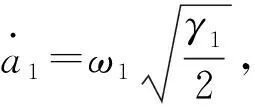
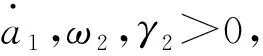
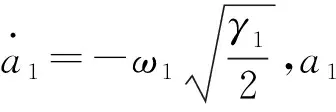
因此，在自适应过程中，|s|可能在有限的时间(t3-t1)内离开μ邻域，并保证其始终停留于一个更大的邻域μ1，即|s|≤μ1，下面估计μ1邻域的界.

根据式(9)和式(11)，有

再根据不等式(13)，可将上述不等式化为

(17)

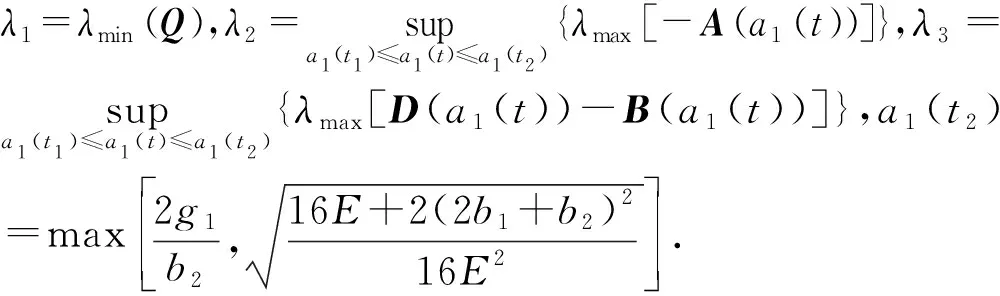
在|s(t1)|=μ的初始条件下，求解微分不等式(17)，可得到:

‖ζ(t)‖≤

上式可得到t2时刻‖ζ‖的最大值，为了估计此时|s|的最大值，令等式(14)中σ=0，可获得|s(t2)|的最大估计值μ1=|s(‖ζ(t2)‖)|.

定理1得证.

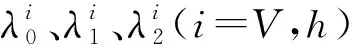
4 数值仿真

4.1 仿真1

为验证滑模微分器对反馈线性化过程中非匹配不确定性的抑制作用，进行仿真1. 仿真结果如图3所示.

图3 仿真1结果

为体现非匹配不确定性的影响效果，本文加入较大的不确定性及干扰，从仿真结果图3可以看出，使用滑模微分器估计速度和高度各阶导数的控制器，高度和速度输出信号均能准确地跟踪上指令信号，而未使用滑模微分器的控制器在接近100 s时已经发散，可知在存在较大不确定性及干扰的情况下，忽略反馈线性化过程中的非匹配不确定性，是不合理的，设计出的控制器可能无法达到预期控制效果.

4.2 仿真2

为验证本文控制算法既快速又平滑的特性，进行仿真2，选择3种控制器：1)选取m=4的快速且平滑的超螺旋滑模控制(FSSTC)器；2)选取m=2的快速但不平滑的超螺旋滑模控制(FNSSTC)器；3)传统超螺旋滑模控制(STC)器.仿真结果如图4所示.

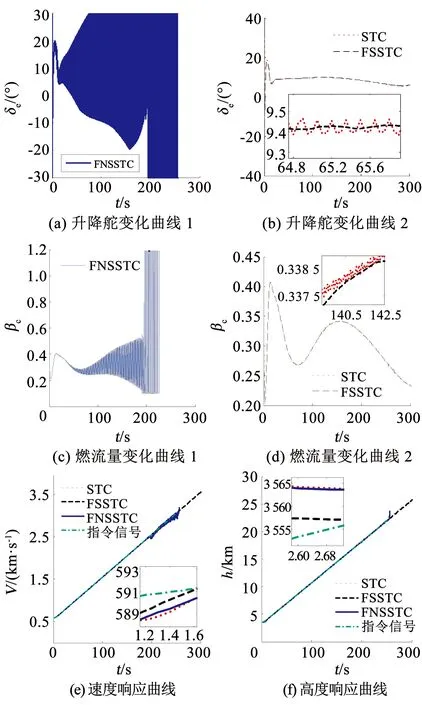
图4 仿真2结果

注本文的控制算法中引入了线性项，原理上收敛速度较传统二阶滑模控制算法要快，但是设计自适应律可能减小其收敛速度，又由于本文设计的自适应律，其参数既可增大又可减小，不会造成参数过大估计，即可选取较大的初始值，保持更快收敛速度.

5 结 论

1)本文针对高超声速飞行器爬升段的控制问题,提出了一种快速平滑的自适应二阶滑模控制算法.

2)鉴于反馈线性化过程中存在的非匹配不确定性，采用了滑模微分器来逼近反馈线性化模型中速度和高度的各阶导数，同时为改善传统超螺旋控制算法的收敛速度以及控制输入平滑性，在其算法中加入了线性项，并将积分项中的符号函数项进行了连续化.

3)仿真结果表明，加入滑模微分器后，成功消除了非匹配不确定性的影响，且该方法有较好的跟踪性能，与传统STC算法和FNSSTC算法相比，有更快的收敛速度，且控制输入平滑，基本消除了抖振.

4)实际应用中，控制输入多为机械运动，意味着控制输入越平滑，则具有更好的工程实用价值.