平均化屈服准则及其在管道失效解析中的应用
2020-12-15章顺虎李寅雪姜兴睿田文皓
章顺虎,李寅雪,姜兴睿,邓 磊,田文皓
(苏州大学 沙钢钢铁学院,江苏 苏州 215021)
屈服准则是判定材料在各种应力状态下是否发生塑性变形的依据,也是求解材料成形外力必须依赖的条件.合理的屈服准则对材料的选择、工艺参数的优化以及工程结构件的安全评定具有重要意义.自20世纪以来,研究者在屈服准则方面做了大量的研究,并取得了许多重要的成果.
1776年,Coulomb[1]提出一个屈服假定,即当某平面上的剪应力超过该平面上材料的内聚力和摩擦力之和时,材料就发生剪切屈服.该准则也因此被称为Coulomb准则.1864年,Tresca[2]在冲裁和挤压实验的基础上,提出了Tresca屈服准则.该准则假定,无论在何种应力状态下,当物体内某一点的最大切应力达到某一定值时,物体就发生屈服.1913年,von Mises[3]从数学的角度出发,提出以偏差应力张量的二次不变量作为判据,建立了Mises屈服准则.该准则随后由Hencky[4]进行了物理解释,即当材料内部所积累的单位体积变形达到一个临界值时,材料发生塑性变形.1950年,Hill[5]将适用于各向同性材料的Mises屈服准则推广到各向异性材料,提出了Hill屈服准则.1952年,Drucker等[6]在Mises屈服准则的基础上,考虑到静水压力对材料屈服的影响进而提出了Drucker-Prager屈服准则.为了统一表征各屈服准则,文献[7]引入了三维应力空间的概念,描述了Tresca准则和Mises准则的几何特征.1985年,俞茂宏等[8]提出了双剪应力(TSS)屈服准则,即假定当两个较大的主剪应力之和达到临界值时,材料发生塑性变形.近年来,章顺虎[9]在线性屈服准则的开发方面也取得了进展,提出了与Mises圆周长相等的线性屈服准则.2015年,杨凤等[10]基于材料屈服时应力之间的关系,提出一种新的各向同性屈服准则.该准则包含了应力幂次在1~4之间的各种形式.2017年,高江平等[11]提出三剪应力统一强度理论,认为当作用于菱形十二面单元体上的3个主剪应力所组成的函数达到某一极值时,材料发生破坏.
以上屈服准则的开发为各类工程结构件的塑性失效分析提供了基础.管道作为石油与天然气的输送媒介,在国民经济中发挥着至关重要的作用.然而,近年来管道安全事故频发,已造成了严重的经济损失.因此,进行管道失效分析具有重要意义.管道塑性失效分析主要用于确定受力管道的极限承载能力,称为爆破压力.国内外已有不少预测管道爆破压力的研究报道.李灿明等[12]采用MY准则求解X80管线钢爆破压力,得到逼近Mises结果的解析解.文献[13-14]应用Tresca屈服准则和Mises屈服准则分别对管道的爆破压力进行了预测,研究发现Tresca准则的预测结果提供了管道爆破压力的下限,而Mises准则的预测结果会比实际数值偏高.彭星煜等[15]利用双剪应力(TSS)屈服准则得到的预测值是管道爆破压力的上限.基于以上研究可见,Tresca屈服准则通常给出下限解,TSS屈服准则通常给出上限解;Mises屈服准则给出相对偏高的结果.
根据上述信息,本文提出了一种新的线性屈服准则,旨在获得更加合理的预测结果,并分析不同屈服准则以及主要参数对管道爆破压力的影响.
1 三经典屈服准则
Tresca[2]屈服准则的表达式为
fTresca=σ1-σ3=σs.
(1)
式中:σ1为第一主应力,σ3为第三主应力,σs为屈服强度.
Tresca屈服准则是一个线性准则,但由于只考虑了两个主应力分量,在描述金属材料的实际塑性变形方面存在不足,即通常会给出偏低的力学参数结果.
Mises[3]屈服准则的表达式为
(2)
根据前人的研究和验证,大多数金属材料的塑性变形满足Mises屈服准则.然而,由于其表达式的非线性,不便于复杂力学方程的联解计算.
TSS[8]屈服准则的表达式为
(3)
TSS屈服准则也是一个线性的屈服准则,但与其他准则相比,它总是提供上限解.
上述公式在π平面上的屈服轨迹见图1,其中Mises屈服准则的轨迹是一个圆,Tresca屈服准则的轨迹是Mises圆的一个内接正六边形,TSS屈服准则的轨迹是Mises圆的一个外切正六边形.
2 平均化屈服准则
2.1 数学表达式
为了线性逼近Mises圆,可以在Tresca屈服准则和Mises屈服准则之间构建一个十二边形.在图1中,Mises屈服准则的外切六边形(TSS)的边心距为OB′,内接六边形(Tresca)的边心距为OF,设线段BF上有一动点E,连接B′E,定义为本文即将开发的平均化屈服准则,OI为其边心距.
在图中,设OB′与OI之间的夹角∠B′OI为θ,则当θ=0°时,OI=OB′;当θ=30°时,OI=OF.可见,OI可在OB′与OF之间变化.
(4)
基于上式,可得
(5)
Mises屈服轨迹上的偏差矢量模长为
(6)
平均化屈服准则的偏差矢量模长为
OE=0.799 3σs.
(7)

图1 π平面上的屈服轨迹
由此可见,平均化屈服准则的偏差矢量模长比Mises屈服准则的小,即E点在F、D之间.在误差三角形OBB′内各种屈服准则的相互关系如图2所示.
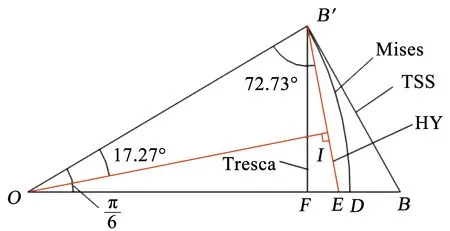
图2 平均化屈服准则在误差三角形内轨迹
下面建立直线A′E、B′E在Haigh-Westgarrd空间中的应力方程.图3为主应力分量在π平面上的投影,其中E点的应力状态为
(8)
假定直线A′E满足如下方程:
σ1-a1σ2-a2σ3-c=0,
(9)
则当材料发生屈服时有c=σs、a1+a2=1,代入应力分量式(8)可得
a1=0.231,a2=0.769.
(10)
将式(10)代入式(9),可得A′E的方程为
(11)
同理,直线B′E的方程可确定为
(12)
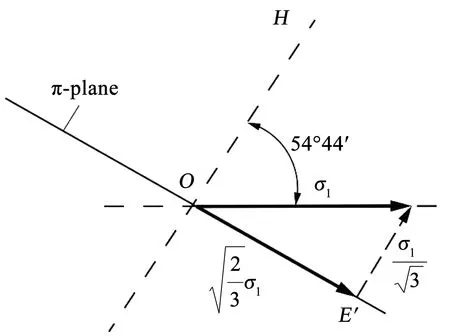
图3 σ1在π平面上的投影
式(11)和式(12)即为所提的屈服准则的数学表达式,它是主应力分量的线性组合.因该准则的边心距OI由积分中值定理计算而得,故导出的准则称为平均化屈服准则,简称HY准则.
由图2可知,HY准则的轨迹在Mises圆内,各顶角计算如下:
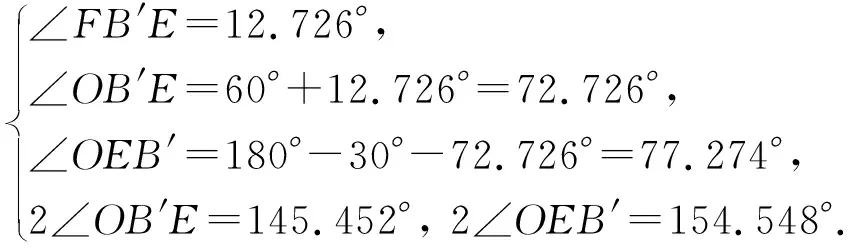
(13)
由图1和式(13)表明,HY准则的轨迹是在Mises圆内的等边非等角的十二边形,边长为0.418 5σs,6个顶点在Mises圆上,内接点顶角为145.452°,另外6个顶点位于Mises圆的内侧,相距0.02σs,顶角为154.548°.
HY准则的轨迹与Tresca屈服准则和Mises屈服准则轨迹之间的绝对和相对误差如下:
(14)
式中:ΔAT1、ΔAT2分别为HY准则和Tresca屈服准则之间的绝对误差和相对误差,ΔAM1、ΔAM2分别为HY准则和Mises屈服准则之间的绝对误差和相对误差.
式(14)表明HY准则的轨迹位于Tresca屈服轨迹和Mises屈服轨迹之间,并且更接近Mises屈服轨迹.
2.2 实验验证
在主应力状态为σ1≥σ2≥σ3时,引入Lode参数来对比不同的屈服准则,Lode参数表达式为[16]
(15)
将上式分别代入Tresca准则、Mises准则、TSS屈服准则和HY准则可得到它们含Lode参数的改写式如下:
Tresca:

(16)
Mises:
(17)
TSS:
(18)
HY:
(19)
基于以上改写式,并结合已有的实验数据[16-19],可以得到图4.

图4 屈服准则实验结果对比
由图4可知,TSS屈服准则位于最上侧,提供了计算结果的上限,Tresca屈服准则位于底部,提供下限;HY准则介于TSS准则与Tresca准则之间,靠近Mises准则结果,且与实验数据吻合较好,提供了较合理的中间结果.
3 管道失效分析
为了证明新提出的HY准则的应用价值,本节将HY准则应用于内压直管道的塑性失效分析.
3.1 爆破压力模型
对于受内压力的薄壁管,其主应力分量表示为
(20)
式中:θ、z、r分别为管道的周向、轴向和径向;d和t是管道的内直径和初始壁厚;p是管道的内部压力.
对于埋地管道,轴向应变通常很小,可看作εz=0.因此,主应变分量为
(21)
式中d0、t0为管道的初始直径和初始壁厚.
当塑性变形发生时,管线钢的应力-应变关系用以下幂函数表示[14]:
(22)
通过式(20)~(22)和失效条件∂p/∂ε=0,则基于式(11)的爆破压力为
(23)
该式表明,爆破压力是应变硬化指数、初始厚径比以及工程抗拉强度的函数.根据上述分析过程,还可以导出基于Tresca,Mises和TSS屈服准则的爆破压力:
(24)
(25)
(26)
上述爆破压力公式的一般形式表示为
(27)

3.2 实验验证和参数分析

图5 理论爆破压力与实验数据的比较
由图5可知,基于HY准则得到的理论管道爆破压力介于Tresca与TSS准则预测的爆破压力之间,与Mises准则结果最为接近,且比Mises准则结果更接近实验结果.
不同硬化指数和厚径比对爆破压力的影响见图6、7.

图6 应变硬化指数对爆破压力的影响
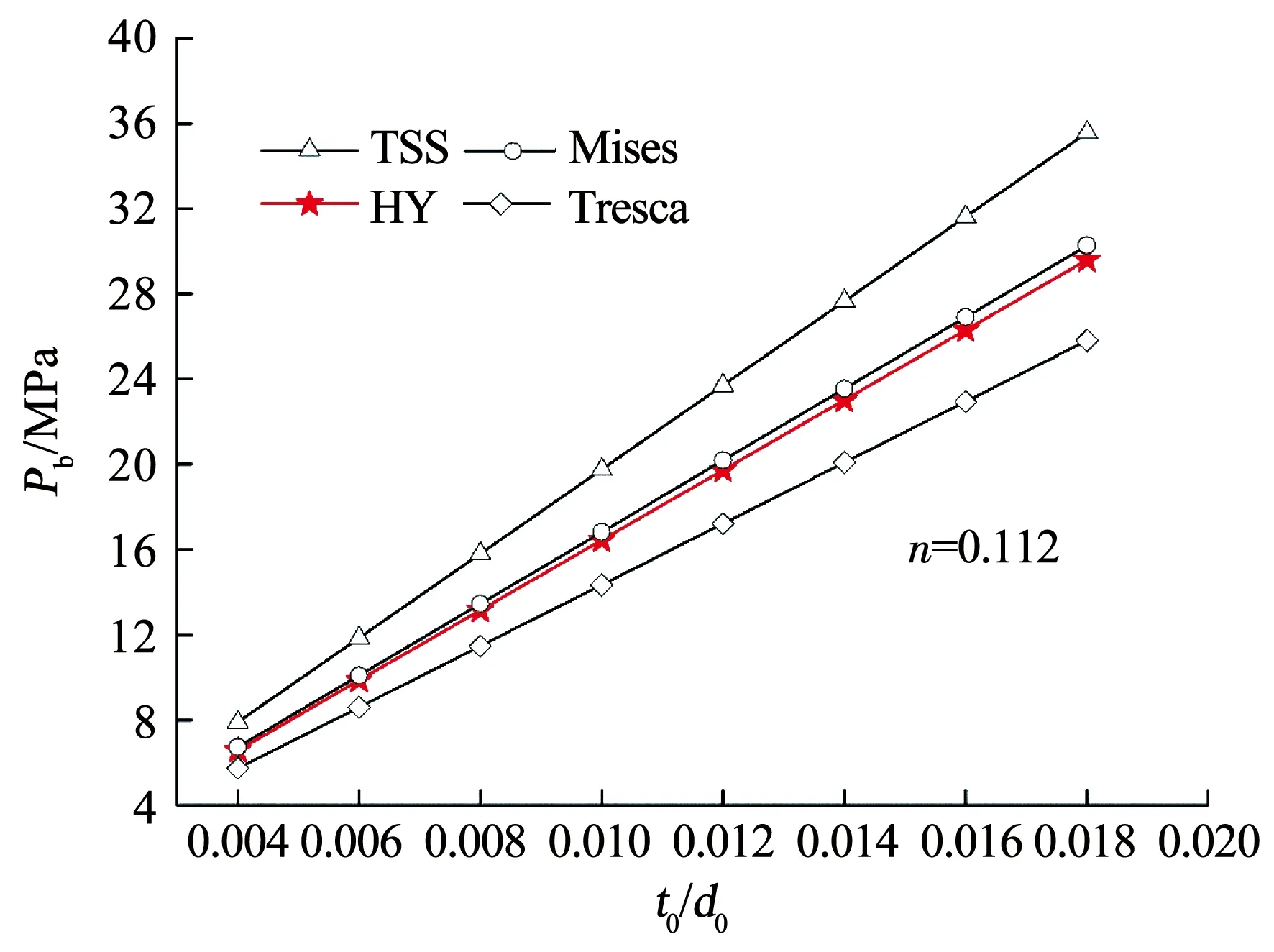
图7 厚径比对爆破压力的影响
由图6、7可知,应变硬化效应和管道尺寸均对管道爆破压力产生影响,管道爆破压力随着应变硬化指数的增大而减小,随管道厚径比的增大而增大.
由于硬化指数取决于钢材生产工艺及化学成分,而厚径比又与使用条件及设计要求密切相关.因此设计管道时要综合考虑这两个关键参数,以避免管道失效.
4 结 论
1)本文提出的平均化屈服准则是关于主应力分量的线性组合,它在π平面上的屈服轨迹为一个在Mises圆内的等边非等角十二边形,边长为0.418 5σs,顶角分别为154.548°与145.452°,与Mises准则之间的最大误差不超过2.1%.通过对比实验数据发现,该屈服准则的预测结果与实验数据吻合较好,给出了较为合理的中间结果.
2)将新提出的屈服准则应用于管道失效分析,结果表明,理论爆破压力取决于不同的屈服准则,并且本文结果与实验数据吻合较好.由此可见,本文采用HY准则进行管道失效分析的方法是可行的.
3)对各种爆破压力的变化规律分析发现,随着应变硬化指数的增加,爆破压力减小;随着厚径比的增加,爆破压力增加,表明管壁较厚或直径较小的管道可以承受更大的压力.
