极限状态下的桁架梁及其等代梁的有限元分析

徐靓玲 陈焰周

(中南建筑设计院股份有限公司，湖北 武汉 430071)

1 概述

1.1 桁架梁等代原则

梁主要为受弯构件，从设计的角度提出桁架梁与钢梁之间的三个等代原则：1)两者能够承受的弯矩一样；2)两者都率先在受弯状态下发生破坏；3)两者的重量相差无几。

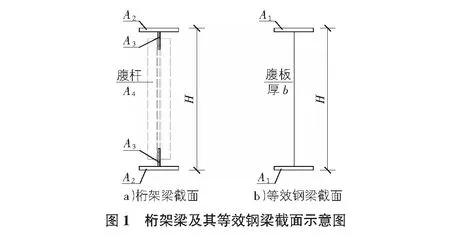
图1给出了桁架梁及其等效实腹钢梁的截面示意，其中符号代表含义如下：H—梁高;A1—等代实腹梁的上/下翼缘面积;b—等代实腹梁腹板厚度;A2—桁架梁上下弦杆翼缘面积;A3—桁架梁上下弦杆的腹板面积;A4—桁架梁腹杆中单角钢的截面积。

根据二者承受弯矩相同可以推出：

(A2+A3)≈A1+bH/6

(1)

使A1=A2，则：

A3≈bH/6

(2)

根据两者重量基本相同可以得到：

2(A2+A3+A4/cosθ)≈2A1+bH

(3)

其中,θ为腹杆与弦杆的夹角。

代入A1=A2，A3≈bH/6，则：

A4/cosθ≈bH/3

(4)

根据破坏发生在受弯状态，拟定梁承受最大弯矩为M，最大剪力为V：

1)对于实腹钢梁，最大弯矩假定由翼缘承担，最大剪力假定由腹板承担，根据受弯先于受剪破坏，可以得到：

(5)

2)对于桁架梁，最大弯矩假定由弦杆承担，最大剪力假定由腹杆承担，弦杆与腹杆的夹角设为45°，根据受弯先于受剪破坏，结合上述推导结果，并适当简化可以得到：

b>3VA1/M

(6)

综上，等效实腹钢梁的腹板厚度应满足式(6)的要求。

上述分析基于等代原则给出了等代梁的腹板厚度和桁架梁弦杆、腹杆尺寸的确定办法。

1.2 钢桁架主梁分析

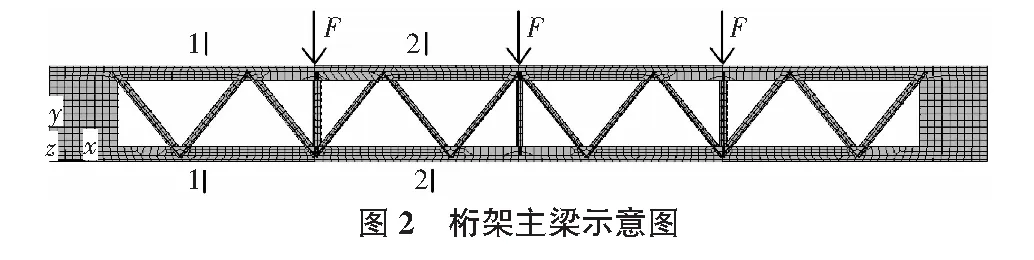
假定一钢桁架主梁，18 m跨，高度为2.0 m，其上每隔4.5 m均匀分布F=1 650 kN的荷载，如图2所示。不难推算截面1—1范围内最大剪力V1=2 475 kN，截面2—2范围内最大剪力V2=825 kN，梁端最大弯矩M1=9 282 kN·m，中间段最大弯矩M2=5 569 kN·m。按照1.1所述的等代分析方法，考虑实际因素，如荷载分项系数、弦杆承受板荷载产生的节间弯矩等，1—1段的桁架弦杆T型截面取T450×300×22×52，腹杆截面取2L200×24，对应的实腹钢梁为H450×2 000×19×52；2—2段的桁架弦杆T型截面取T450×300×16×34，腹杆截面取2L140×14，对应的实腹钢梁为H450×2 000×7×34。

1.3 钢桁架次梁分析

假定一钢桁架次梁，两端支座按铰接考虑，18 m跨，高度为1.5 m，承担均布荷载Q=80 kN/m，如图3所示，易得分段1内最大剪力V1=720 kN，最大弯矩M1=2 430 kN·m，分段2内最大剪力V1=360 kN，最大弯矩M2=3 240 kN·m。按照1.1所述的等代分析方法，同样考虑弦杆需承受板荷载产生的节间弯矩等影响因素，分段1范围内桁架弦杆T型截面取T300×250×16×24，腹杆截面取2L125×12，对应的实腹钢梁为H300×1 500×7.5×24；分段2范围内桁架弦杆T型截面取T300×250×14×30，腹杆截面取2L100×10，对应的实腹钢梁为H300×1 500×4.5×30。

2 有限元对照分析

2.1 桁架主梁及等效钢梁极限状态下的应力分析

按照图2中的加载方式，在分析软件中查看桁架主梁及其等效钢梁在极限状态下的整体应力状态、上下翼缘应力状态以及桁架梁的腹杆和等效实腹钢梁的腹板应力状态，可以得出以下结论：1)从应力分布状态及应力值来看，桁架梁上下弦杆翼缘与等效实腹钢梁上下翼缘基本一致，两端及中部全截面进入屈服。2)桁架腹杆以及等效钢梁全截面进入屈服。3)桁架梁与等效钢梁的受力失效过程如下：桁架梁上下弦杆翼缘(等效钢梁上下翼缘)两端部分进入屈服→桁架梁腹杆翼缘在次弯矩作用下局部开始进入屈服→桁架梁上下弦杆翼缘(等效钢梁上下翼缘)中间部分进入屈服→桁架梁腹杆(等效钢梁腹板)全截面进入屈服→构件失效。

2.2 桁架次梁及等效钢梁极限状态下的应力分析

按照图3中的加载方式，在分析软件中查看桁架次梁及其等效钢梁在极限状态下的整体应力状态、上下翼缘应力状态以及桁架梁的腹杆和等效实腹钢梁的腹板应力状态，可以得出以下结论：1)从应力分布状态以及应力值来看，桁架梁上下弦杆翼缘与等效钢梁上下翼缘基本一致，端部及中部全截面进入屈服。端部屈服位置为桁架梁腹杆开始连接处以及等效钢梁腹板厚度改变处。2)桁架腹杆以及等效钢梁全截面进入屈服。3)桁架梁与等效钢梁的受力失效过程如下：桁架梁上下弦杆翼缘(等效钢梁上下翼缘)中间部分进入屈服→桁架梁腹杆翼缘在次弯矩作用下局部开始进入屈服→桁架梁上下弦杆翼缘(等效钢梁上下翼缘)两端部分进入屈服→桁架梁腹杆(等效钢梁腹板)全截面进入屈服→构件失效。

3 考虑桁架梁平面外变形下的极限承载力

在本节中，主要分析桁架梁在考虑平面外变形下的极限承载力。

3.1 桁架主梁分析

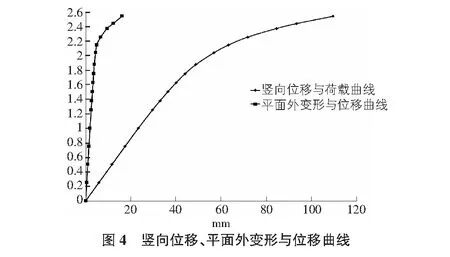
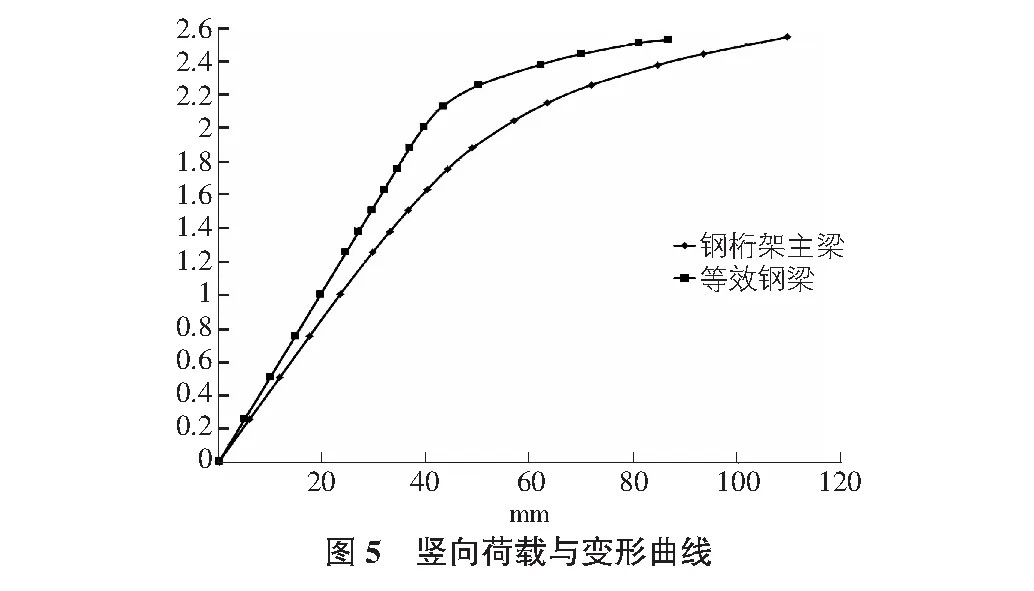
图4为竖向荷载作用下桁架主梁的竖向位移曲线和平面外变形曲线，其中X轴表示构件最大变形，Y轴数值为设计荷载的倍数；图5为竖向荷载作用下钢桁架主梁与等效钢梁的全过程竖向变形曲线，其中X轴表示构件竖向最大变形，Y轴数值为设计荷载的倍数。

从图4中可以看出：1)桁架梁竖向位移曲线在1.4倍设计荷载时，位移曲线开始由直线变为曲线，而平面外变形曲线要到2.0倍设计荷载之后开始由直变曲，表明桁架主梁平面外失稳晚于面内桁架梁翼缘屈服。2)桁架梁面外变形较竖向位移小较多。3)桁架梁的极限承载力与图5中承载力相当，表明桁架梁构件面外失稳没有明显影响构件承载力。4)桁架梁以构件面外失稳控制的承载力可取2.0倍设计荷载。5)桁架梁以构件不显著进入屈服阶段控制的承载力可取1.4倍设计荷载。

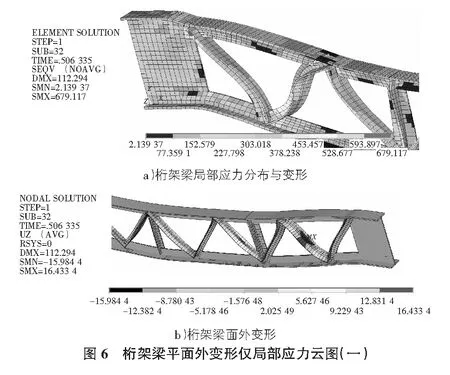
图6给出了桁架梁在极限状态下的平面外变形图及局部应力云图。从图6可以看出，桁架梁面外变形较大的构件为腹杆。

3.2 桁架次梁分析

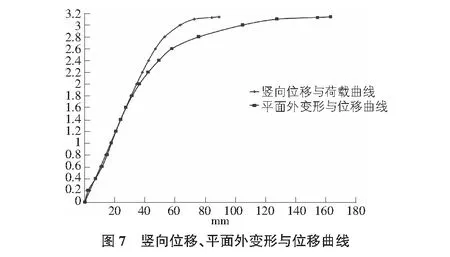
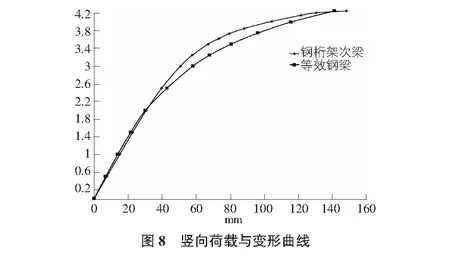
图7为竖向荷载作用下桁架次梁的竖向位移曲线和平面外变形曲线，其中X轴表示构件最大变形，Y轴数值为设计荷载的倍数；图8为竖向荷载作用下钢桁架次梁与等效钢梁的全过程竖向变形曲线，其中X轴表示构件竖向最大变形，Y轴数值为设计荷载的倍数。

从图7中可以看出：1)桁架梁竖向位移曲线在1.6倍设计荷载时，位移曲线开始由直线变为曲线，而平面外变形曲线在2.0倍设计荷载之后开始由直变曲，表明桁架梁平面外失稳与面内桁架梁翼缘屈服基本同步。2)桁架梁面外变形与竖向位移量基本相当。3)桁架梁的极限承载力与图

8中承载力相差明显，表明桁架梁构件面外失稳显著减小了构件承载力。图8中桁架梁极限承载为4.2倍设计荷载，而考虑桁架梁平面外失稳后的极限承载力不到3.1倍设计荷载，减小较多。4)桁架梁以构件面外失稳控制的承载力可取2.0倍设计荷载。5)桁架梁以构件不显著进入屈服阶段控制的承载力可取1.6倍设计荷载。

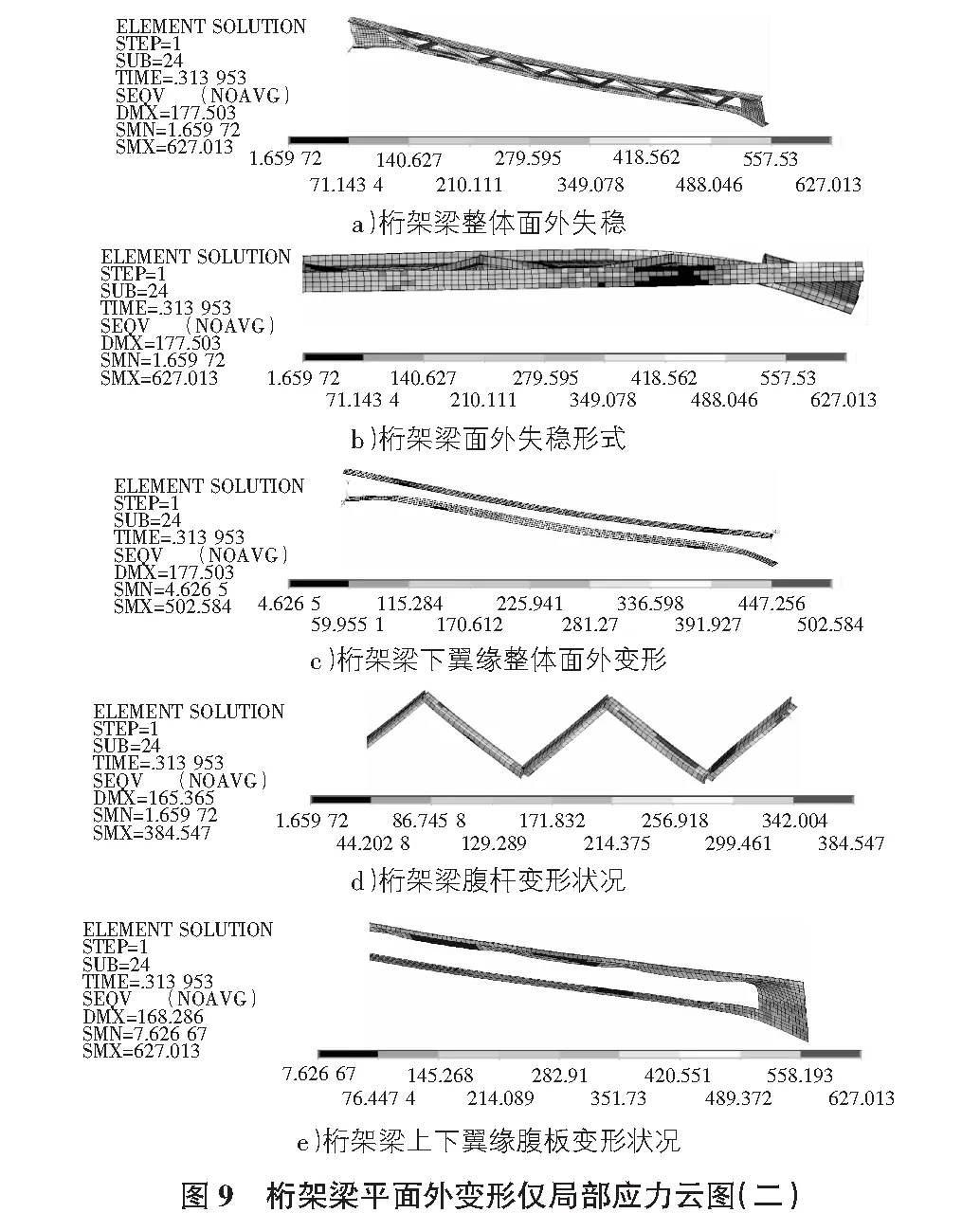
图9给出了桁架梁在极限状态下的平面外变形图及局部应力云图。从图9可以看出：1)桁架梁面外变形主要为桁架梁下翼缘，变形位置主要集中在两端第一节腹杆内的翼缘部分。2)桁架梁的腹杆面外变形不大。3)桁架梁两端连接板面外变形显著。

3.3 面外失稳状态分析

对于桁架主梁与次梁面外失稳的状态不一样，这主要是由桁架主梁与次梁的两端约束不一样。对于桁架主梁，两端与框架柱连接，两端约束为固结，在竖向荷载作用下桁架下翼缘端部虽然受压，但是由于面外弯曲约束较强较难出现面外变形，最终加载到一定阶段受压腹杆面外屈曲；对于桁架次梁，两端与框架主梁连接，两端约束一般认为为铰接，翼缘的面外转动基本没有约束，因而在竖向荷载作用下桁架下翼缘首先发生面外变形。

4 结语

1)桁架主梁与次梁在竖向荷载作用下的平面外变形不同，桁架主梁为受压腹杆面外屈曲，而桁架主梁为下翼缘首先发生面外变形。2)对于本工程设计的桁架梁，以构件面外失稳控制的承载力，桁架主梁及次梁可取2.0倍；以构件不显著进入屈服阶段控制的承载力，桁架主梁可取1.4倍，桁架次梁可取1.6倍。计算中采用的是钢材的屈服强度345 N/mm2，而转化为设计值时应乘以0.8，因而若以构件不显著进入屈服阶段控制的承载力，桁架主梁可取1.12倍设计荷载，桁架次梁可取1.28倍设计荷载，富裕度不大。3)对于桁架主梁和次梁，桁架梁面外变形和竖向位移两者间差异不同，同时桁架梁构件面外失稳对构件承载力的影响对于主梁和次梁也显著不同。