基于有限元分析的浮选多相流研究
2020-12-15尹洪月马永杰殷雨峰王大硕
尹洪月 马永杰 殷雨峰 王大硕 曹 阳
(黑龙江科技大学 矿业工程学院,黑龙江 哈尔滨150022)
基于ANSYS有限元对浮选多相流进行研究,就目前国内选煤厂而言机械搅拌式浮选机被广泛应用,但由于其可视性差,且浮选机内流体状态复杂,因此研究浮选机内多相流很是困难。但本次项目采用有限元分析方法,可以即快捷又高效的模拟浮选机内的流体状态,并分析浮选机内流体的状态并给出可靠的动力学方程,并可用于浮选机的工艺参数优化指导生产,因此具有较广阔的应用前景。
1 有限元分析法
定义。其基本思想是将求解区域用矩形网格代替,网格线的交点为计算节点,每个节点与相邻的四个网格组成一个计算单元,即一个计算单元由一个中心节点与一个相邻节点组成。在每个单元中函数的近似解不是像有限元方法那样采用单元基函数的线性组合来表达,而是以单元中未知函数的分析解来表达。为了获得单元中的分析解,单元边界条件采用插值函数来逼近,在单元中把控制方程中非线性项局部线性化,并对单元中待求函数的组合形式做出假设,找出其系数,用单元边界节点上待求函数值来表达。虽然有限分析解获得的是求解区域中离散点的函数值,但是由于每个单元内部都有与其中心节点对应的分析解表达式,因此有限分析解在每一个节点的局部区域内都是连续可微的,这对于需要计算求解函数导数的计算流体力学问题具有明显的优势。
2 有限元模型的建立
2.1 转子模型的建立。转子应用材料为Q235A,该材料屈服极限为265MPa、材料许用应力为157MPa、弹性模量2.1×105N/mm2、泊松比为0.3、质量密度为7850kg/m3、热膨胀系数为273.33×10-5K、切边模量80GPa。进行网格划分和模型如图1 所示。

图1 网格划分模型
2.2 边界条件及加载。根据浮选机的实际使用状况,将槽底的8 块座板设置为固定约束,在槽底表面施加P=3.8×104Pa 的压力,其他各处保持不变,不加约束。
2.3 求解及结果分析。按上述边界条件加载后,对该模型进行求解,其等效应力云图如图2 所示,位移矢量和图如图3 所示。

图2 初步设计的槽底应力云图
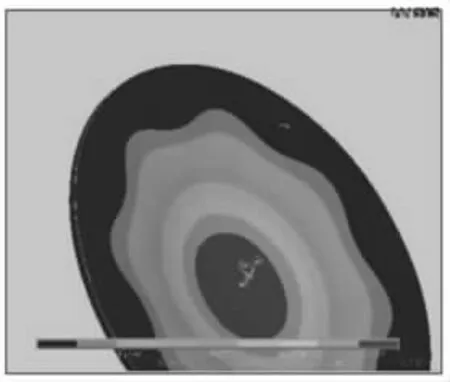
图3 初步设计的槽底位移矢量和图的槽底应力云图
由图2 可知,根据弹性理论计算时,其应力最大点是在靠近槽底中心方向的座板与肋板的连接处。在工作情况下,槽底载荷的最大Von-mises 应力为σmax=692.16MPa>[σ],在许用应力范围内,其他区域应力不超过163.186MPa。由此可见,该结构中存在着明显的应力集中现象,且不能满足强度要求,需进一步改进。
由图3 可知,在槽底中心区域出现了较大的矢量和位移。通过理论受力分析可得知,该位移主要为受力变形,为达到减小槽底中心位移量的目的,需从提高结构弯曲刚度方面考虑优化改进。
3 单一液相流模拟与分析
3.1 数值模拟策略。
3.1.1 湍流模型的选择。在大量专家学者的试验,通过大量的计算与实践总结众多的模型,包括雷诺应力模型、大涡模拟模型、Spalart-Allmaras 模型、k-ω 模型、k-ε 模型在内的经典数学模型。搅拌流场中应用最多的是Spalding 和Launder 提出的标准k-ε模型[8]。该模型主要求解湍流动能k 和湍流耗散率ε,将二者与湍流涡粘系数μt 建立相应的关系,k 方程的求解较为精确,但是,ε方程是经过经验公式推导出来的。因为标准k-ε 模型简单、计算精度高等特点,于是该模型得到广泛应用。在标准k-ε 模型的推演中引入了Boussinesq 假设和v=Ck2/ε 的关系式,特征速度以湍流动能的形式反应,特征长度的尺度用湍流动能耗散率进行表征,使k-ε 在流场数值模拟过程中有以下两个独到之处。
在前期作用中,考虑到流场中各个流动点的湍流动能传递和流动,没有根据经验设定其特征长度,而是通过耗散尺度进行表征的。
标准k-ε 模型的湍流动能方程(k 方程)为:
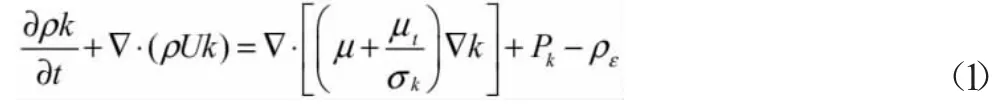
标准k-ε 模型的湍流动能方程(ε 方程)为:
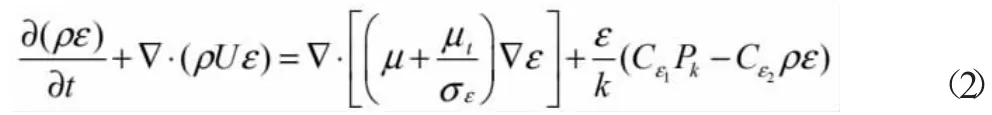
Pk是粘性力和浮力的湍流产物,其方程为:
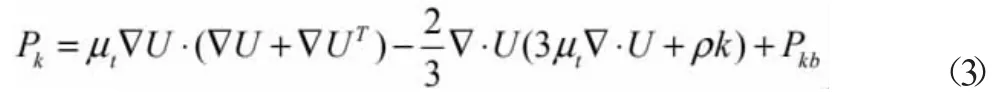
3.1.2 壁面的边界条件。流体在壁面处的流动状态可设置为两种,分别为无滑移和自由滑移,具体的选择,需要根据数值模拟的情况。根据无滑移壁面的特性和条件,其适用于壁面间与流体相互作用的流体模拟;自由滑移条件适用于壁面与流体无相互作用、流体在与界面垂直方向无速度梯度的条件。由于液相粘度对模拟的影响较大,在单一液相数值模拟中,适合采用无滑移边界条件,即No Slip 模型。
3.1.3 动静区域的交界面。在划分旋转域的过程中,会产生交界面,而设置交界面的好坏,会直接影响模拟数值的结果。决定数值模拟精确性的关键所在是固体域与流体域的交界面和流体域内动- 静域交界面的设置。交界面设置需要适合流动域与固定域相对位置保持不变的流场,因此,选择CFX多重参考系坐标中提供的冻结转子模型。
3.2 搅拌导流区流场。
3.2.1 特征。根据以上设定条件的叙述,对于絮凝浮选装置的搅拌导流区进行了单一液相流场的特征数值模拟,其收敛曲线如图4所示,其中由残差收敛曲线(红色线)可以了解到,其残差基本处在0.0015,数值模拟具有很好的收敛性,满足流场数值模拟的应用。采用CFX-Post 后处理模块建立絮凝浮选装置的主视截面和俯视截面,对流场进行分析。
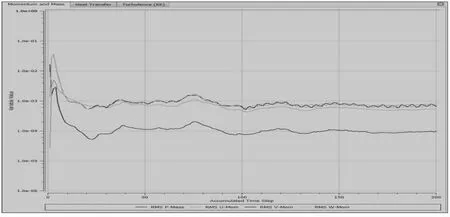
图4 单相流模拟运算收敛图
在搅拌作用下与壁面发生碰撞,改变运动方向,进入到转子上下的两个轴向循环区域内。因为中部循环距离高速旋转搅拌的转子最近,所以受其影响中部循环区域流体的流速比较大,特别是在靠近转子的区域,其速度达到最大值。
3.2.2 搅拌导流区单一液相湍流动能分布特征。由微细颗粒矿物形成大颗粒絮凝体的过程,湍流剪切力起着必不可少的作用,它是絮凝体的成长的主要动力来源的同时,也是会对之前已经成型的大颗粒絮凝体造成相应的破坏。所以在絮凝过程中,对其进行合理的控制至关重要,使其在一个合理的范围内,既能达到既使絮凝体生长的范围,又不会使得已经成型的絮凝体遭到破坏,而湍动能可用来表示湍流剪切力和絮凝体的密实程度,其表示形式为:
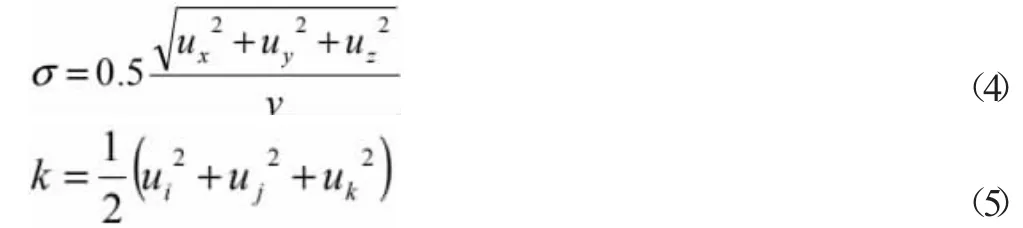
而在所采用的标准k-ε 模型中,湍流动能则表示形式和上面的表达式存在着线性关系。因此采用CFX软件中的湍流动能K值作为搅拌导流区评价标准,也就是在一定范围内,随着k 值的增加,湍流动能也会更加剧烈,同时流场内微涡比例也会增加,从而絮凝效果好。
模拟结果显示,转子叶轮上方位置产生了湍流动能最大区域,其中导流管一侧的湍流动能显然要低于远离导流管区域的湍流动能,这符合了素的分布情况。这主要是由于该处的剪切效果被导流管的导流运输作用减弱了。在转子区域中,叶片的高速旋转驱动流体的运动,从而产生了强烈的湍流动能,而转子的运动是影响湍流强度的主要因素。在转子区域,由于转子的搅拌作用,使流体形成了高速而强烈的湍流脉动,从而该区域发生絮凝反应。在远离转子的其他区域,流体的速度逐渐减小,湍流受叶片运动的影响逐渐减弱,相应的,也降低了流体的湍流动能。这主要是由于流体的粘滞作用和能量耗散引起的,絮凝体的碰撞粘结受益于在该区域内的流体运动,进而使絮凝体的粒径生长较大。
4 结论
单相结果表明,在搅拌流畅的导流区内,存在三个不同的循环区域,自转区域出现最高湍流动能,对矿物颗粒的絮凝有利。计算G值可得到,模拟转速范围在635r/min~870r/min 之间。通过对不同转速、转子位置以及导流筒结构的设置情况进行模拟,得出的优化条件为转子距底350mm,转速800r/min,设置导流筒。此时湍流动能1.425m2s-2,矿浆最大流速1.64m/s。此时的矿浆流动及循环状态最好,整个流场对微细粒矿物的絮凝有利。
