限位挡块对连续梁曲线桥地震响应的影响
2020-12-15蒋林均
蒋林均
(国药集团重庆医药设计院有限公司,重庆400000)
简支梁桥、连续梁桥构造简单,受力明确,施工方便,是桥梁建设中广泛运用的一种结构形式。早期的简支梁桥用油毛毡、石棉或铅板等材料做成“支座”,后来随着橡胶工业的发展,橡胶支座逐渐成为桥梁支座的主流。将主梁直接搁置在橡胶支座上,可以满足静力荷载条件下的变形(位移和转角)需求,也适应由于热胀冷缩和混凝土收缩、徐变等因素引起的变形,从而让桥梁结构按设计的力学模型工作。地震作用下,由于墩梁铰接,结构较“柔”,在一定程度上减小了桥梁的地震反应,使设计师更容易控制好桥梁的强度设计。然而,汶川大地震中百花大桥、龙尾大桥的震害表明[1],梁桥的主梁与桥墩连接较为薄弱,地震中稳定性较差,容易使墩顶与梁底的位移差过大而导致落梁破坏。对于普通非高墩桥梁,在容易加强桥墩强度的前提下,给主梁设置适当的限位块,即能满足桥梁非抗震时的变形需求,也能有效地防止地震作用时因墩和梁间的位移差过大而发生落梁破坏。
变高墩连续梁曲线桥,在我国西部山区使用普遍,其结构形式相对而言比较复杂。相比直线桥,曲线梁桥在主梁的水平面内不规则,地震作用时会出现扭转反应。一般的橡胶支座要么不能受拉,要么抗拉能力远小于抗压能力,有些根据静力条件设计的曲线桥甚至没有设抗扭支座。上述两个原因导致了连续梁曲线容易因墩顶梁底的位移差过大而发生落梁破坏。所以曲线梁桥应重视限位挡块的抗震作用。文章以丽(江)攀(枝花)高速公路陶家渡C 匝道桥的某一联为原始模型,输入1971 年旧金山地震211 号台站记录的地震波,分别计算了该桥在有限位挡块和无限位挡块时的地震响应。对比分析表明限位挡块可以有效的控制墩顶梁底位移差,从而防止落梁的发生。
1 工程概况
文中分析用的模型取自丽(江)攀(枝花)高速公路陶家渡C匝道桥的某一联,此联为四跨变高墩连续梁曲线桥,跨径与墩高见表1,曲率半径为50 米(图1)。桥面在一水平面上,此平面定义为XY平面,主梁圆弧的圆心为坐标系的原点,9#墩与13#台的连线平行于X 轴,Y 轴垂直于X 轴,按右手法则确定Z 轴,整体坐标建立完成。上部结构(主梁)为单箱双室截面,建模时忽略倒角的影响,截面尺寸见图2。全桥使用C40 混凝土。整桥模型见图3。

表1 桥梁路径与墩高

图1 桥梁平面布置图(单位:米)
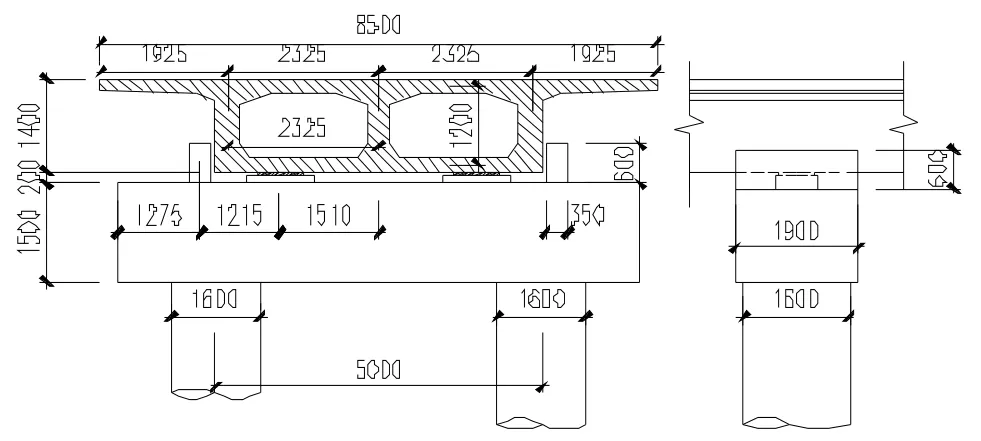
图2 截面尺寸(单位:毫米mm)
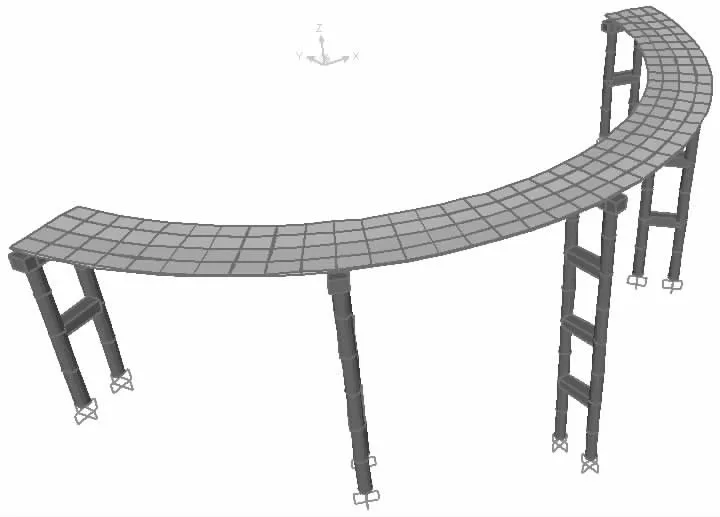
图3 三维有限元模型
2 建立三维有限元模型
2.1 限位挡块
由混凝土现浇而成的限位挡块(挡块尺寸见图2)用框架单元FRAME 模拟,挡块与箱形梁间的净距为5cm。地震作用下,箱形主梁与挡块将会发生碰撞,本文使用SAP2000 的缝单元GAP 来模拟这种碰撞反应。
GAP 在SAP2000 中属于连接单元,其单元属性即非线性力-变形关系如下给定[2]:

f——非线性力
k——弹簧劲度系数
d——单元变形(压为负,拉为正)
open——初始缝宽,必须为零或正值
挡块的侧向刚度为

根据文献[3]缝单元元的弹簧劲度系数k 要比挡块的侧向刚度K档块大一到二个数量级,本文取k=10K挡块。
2.2 支座
该曲线桥中间墩顶(11#墩)设固定支座,其余各墩顶的内侧与外侧分别安装两个GJZF4350×550×72 滑板支座,且对称于箱形梁截面轴线布置。

表2 各工况支座布置表
根据文献[4]《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG D62-2004)第79 页的规定:支座剪变模量Ge=1MPa

根据文献[5]《工程结构减震控制》竖向刚度Kv计算如下:

Ac——橡胶支座有效受压面积
Te——橡胶层总厚度
使用SAP2000 线性连接单元LINK 来模拟GJZF4350×550×72mm四氟滑板橡胶支座,LINK单元的竖向取为Kv,与竖向垂直的两个水平向设为理想的活动铰支座。
2.3 主梁与其他构件
为了更为真实的模拟桥梁在地震作用下的反应,上部结构(主梁)采用壳单元SHELL模拟(忽略倒角),每3 米长度的单箱双室梁由11 张壳单元SHELL组成,每张壳单元的最大边长为3 米。使用“边束缚”让壳单元之间的变形完全协调。
其他结构构件都用框架单元FRAME 模拟,各桥墩墩底为完全固定端约束。
3 时程分析与分析结果
3.1 工况与输入地震波
设置有限位挡块的模型命名为ORIGINAL,无限位挡块的模型称为UNSTRAINER。
下面两张图(参见图4)是本文中用到的地震波加速度时程[6],时间步长0.02 秒,总持时43.68 秒。图4 中加速度值用于时程分析时乘以了23 的放大系数,将Y方向的最大加速度值调为3.0m/s2,X方向的最大加速度值调为2.576m/s2。这对地震波来自1971 年San Fernando地震211 号台站记录。
3.2 时程分析
首先对结构进行自重作用下的分析,再将此分析结果叠加至地震动作用下的模态时程分析,以求分析结果与实际更接进。因此,以下分析结果包括了重力荷载作用效应。结构阻尼使用模态阻尼,且每个模态的阻尼比相同,均为5%。
非线性模态时程分析的动力平衡方程如下[2]:
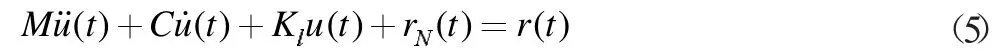
其中M为质量矩;C为结构阻尼矩阵;Kl为线弹性单元(除了连接单元的所有单元)的刚度矩阵;rN为连接单元的从非线性自由度而来的力向量;ü、u觶、u 为相对于地面的相对加速度、速度、位移;r为施加荷载向量。
3.3 结构动力特性
结构动力特性是进行结构动力分析的基础,在抗震设计中首先应对结构进行模态分析,得到结构的自振特性。使用SAP2000 的里兹RITZ向量法,可以为模态时程分析提供更好的基础[2]。模态分析的结果参见表3。
限位挡块与箱形梁的碰撞反应是用非线性连接单元GAP 模拟,非线性单元只有在非线性分析中发挥作用,模态分析属于线性分析,所以工况一与工况二的模态分析结果一致,GAP 单元不会影响模态分析。
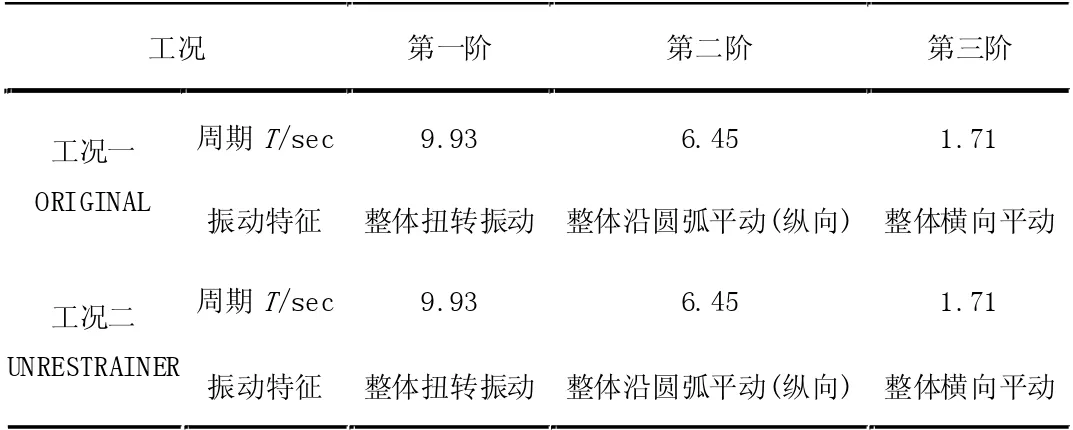
表3 结构动力特性
3.4 梁底面位移
主梁自身纵向刚度很大,故在纵桥向主梁可以近似为刚体。两个工况的分析结果也进一步表明,上部主梁在各墩顶处的切向位移几乎相同。主梁自身的横向刚度远比纵向刚度小,主梁在横向更多的表现为一个变形体,所以横桥向位移在各墩处不相同。
本工程的限位挡块主要是约束横桥向主梁位移,所以在径向位移中,设置了限位挡块的ORIGINAL 工况的计算结果远小于没有设置限位挡块的UNRESTRAINER 工况。限位挡块不但使主梁径向位移减小,而且使主梁在各墩顶的位移大小趋向一致。图5 表明,ORIGINALR 的主梁径向最大位移为11.2cm,UNRESTRAINER 的主梁径向最大位移为65.1cm,挡块的作用十分显著。

图5 梁体位移
3.5 墩顶位移对比
在两个工况中,中间墩与主梁固接,其余墩梁间都视为理想的双向活动支座,所以两个工况的计算都显示中间墩顶的位移大,两边墩顶位移小;中间墩顶的切向、径向位移与主梁在此点处的位移相同,符合力学模型的设置。同样,径向布置的限位挡块对墩顶的径向位移有影响,图6 表明限位挡块减小了墩顶的径向位移。

图6 墩顶位移
3.6 墩顶与主梁位移差
无论是切向还是径向,ORIGINAL的位移差都要小于UNRESTRAINER 的位移差。尤其是图7 的右半幅里,由于限位挡块的作用,9#墩、10#墩、12#墩、13#墩的墩梁位差都在5cm 左右,11#墩因为墩梁固结,所以位移差为0。正是由于限位挡块的作用,在大震作用下,如果限位挡块不失效,主梁与墩底的位移差会得到有效的控制,从而防止落梁破坏的发生。
限位挡块在整过地震作用过程中的作用见图8。图8 为9#墩的径向位移差时程曲线,除中间墩外,其他各墩顶有完全类似的情况。图8 还反映出由于滑板橡胶支座无自动复位工功能,地震结束后墩顶主梁位移差都将存在,需要人工对其复位。

图7 墩顶主梁底位移差

图8 9#墩顶梁底径向位移差时程
3.7 墩底内力对比
挡块设置在桥梁的径向,所以两个工况的墩底切向剪力反应计算结果相近,未见挡块明显改变了墩底的切向剪力。由于该桥是曲线桥,当主梁发生纵向位移时,也会受到挡块的约束作用,类似于中间墩梁在切向的固接,各边墩也会受到这种因挡块而产生的“类固接”的影响,而使边墩的切向剪力增大,中间墩减小,这在图9 左半幅图里表现得较明显。本曲线桥梁虽然是对称结构,但是其平面不规则性导致了弯扭组合效应,没有明确的横桥向和纵桥向,在任何一个水平方向的地震输入都会引起与之垂直的另一个水平方向上的地震反应[7],地震作用下的结构反应将不再对称。图10 表明,考虑的限位挡块与主梁间碰撞作用,将使得反应更加复杂,各墩底的内力分布不规则性将更加明显。限位挡块在一定程度上使桥梁结构变“刚”,所以图10 ORIGINAL 工况的墩底剪力普遍比UNRESTRAINER 工况的大。由于限位挡块在径向的限位作用,各墩在横桥向会协同受力,相较于没有设挡块时,墩底径向剪力反应更趋于均匀,即中间墩略有减小,边墩增大。
墩底弯矩图的变化趋势基本上沿袭了剪力图的特点,图11 中绕切向的弯矩M1 变化规律与图10 径向剪力F2 的变化规律一致,而图12 绕径向的弯矩M2 与图9 切向剪力F1 的变化规律一致。
曲线桥梁平面不规则性导至了弯扭耦合效应,任何一个方向的地震作用都会引起与之垂直方向的反应,从而在构件中产生扭矩。中间墩与主梁固接,在主梁水平面扭转振动的带动下,中间墩底扭矩较大,边墩与主梁在两个水平向的位移没耦合,其扭矩非常小。挡块的设置有让各墩协同承受扭转反应的作用,使中间墩底扭矩减小,两边墩底扭矩增大,但没有实质性的改变扭矩在各墩底的分布状态,即中间墩底扭矩远远大于边墩的墩底扭矩反应,见图13。

图9 墩底切向剪力(单位:kN)

图10 墩底径向剪力(单位:kN)
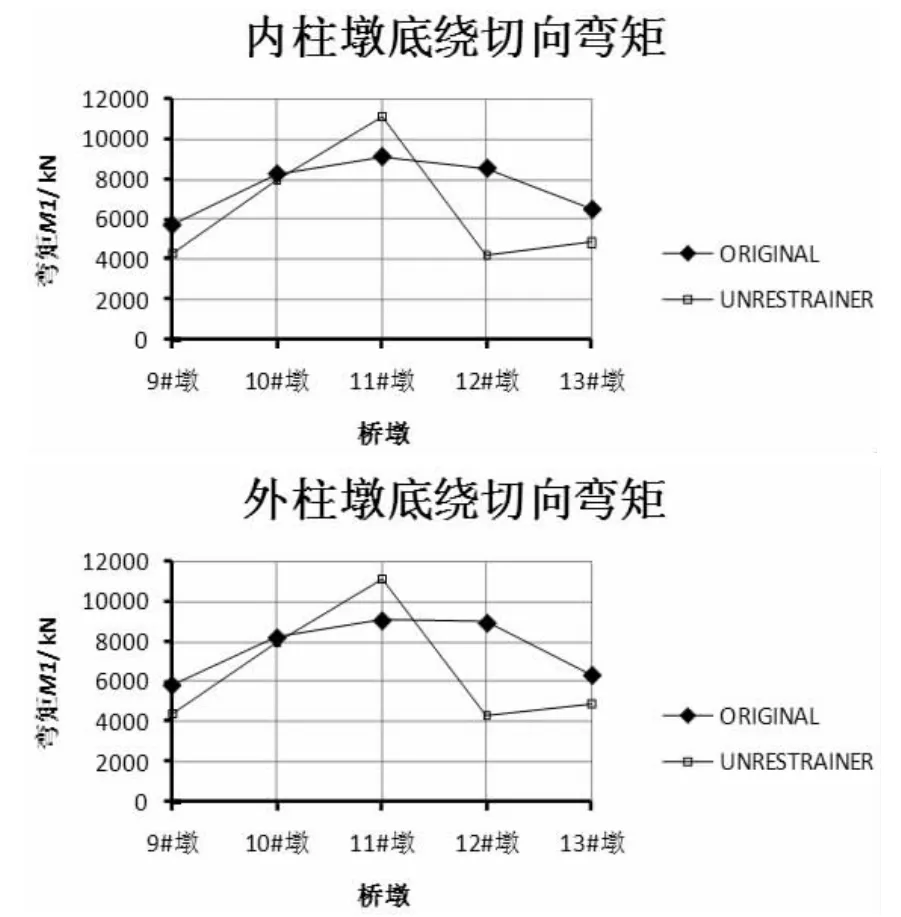
图11 墩底绕切向弯矩(单位:kN·m)
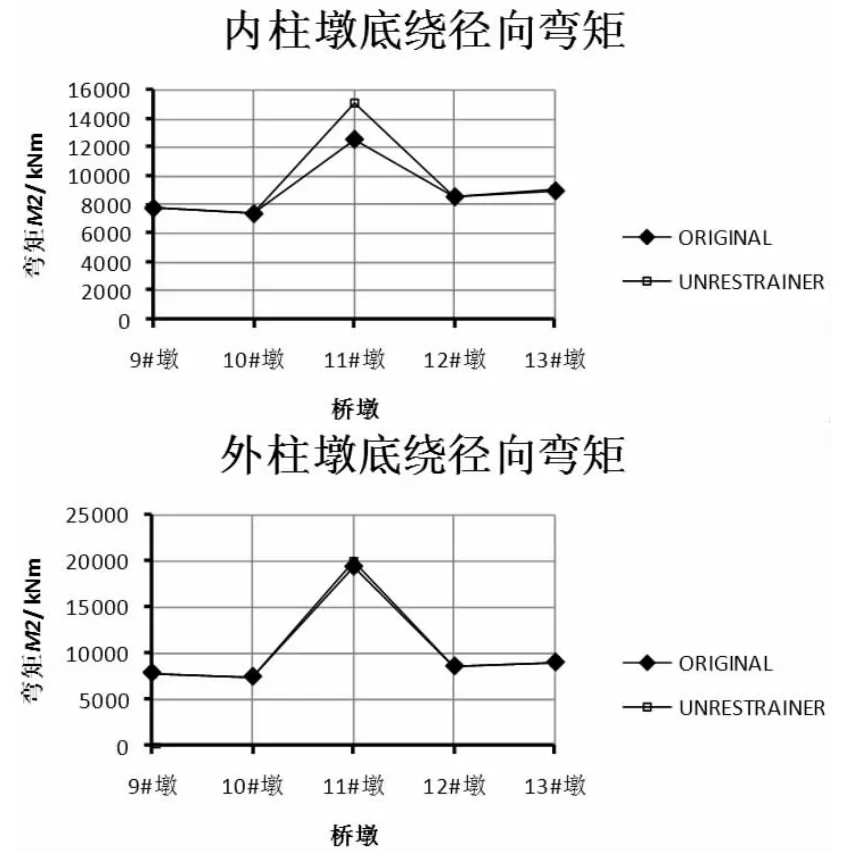
图12 墩底绕径向弯矩(单位:kN·m)

图13 墩底扭矩(单位:kN·m)
3.8 主梁跨中扭矩
运用SAP2000 的“截面切割”[8],将每跨跨中的扭矩提取出来,并制成图14。如3.7 节墩底扭矩所述,跨中扭矩也是曲线桥梁地震反应与直线桥梁的一个重要区别。由于挡块的作用,主梁的跨中扭矩将增大,且由于主梁与挡块的碰撞作用,使跨中扭矩分布不再像UNERSTRAINER 工况那样对称。
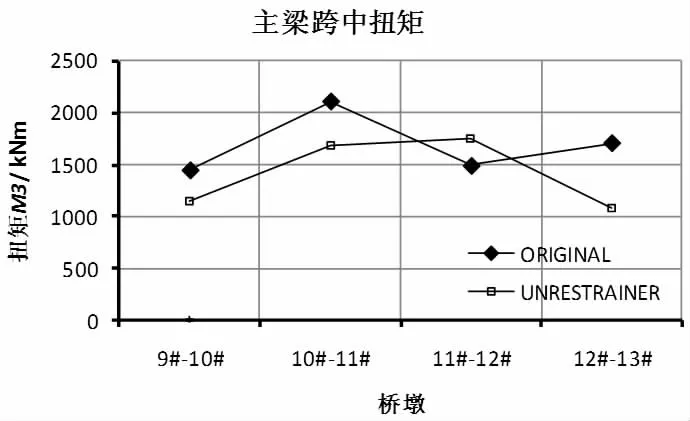
图14 主梁跨中扭矩
4 结论与展望
设有限位挡块的连续梁曲线桥在地震作用下,墩顶与梁底间的位移差将远小于不设挡块的同种桥,能有效的防止落梁破坏。在本文中,如果挡块设计合理,不失效,墩顶位移差可控制在5cm 以内,而无挡块的同一座桥可发生65.4cm的位移差。
挡块也可以减小主梁和墩顶相对于地面的位移反应,尤其是减小主梁的相对位移反应,对一些由位移控制设计的主梁能起到很大的有益作用。设在径向(横向)的挡块,没有实质性的影响桥梁在切向(纵向)的内力、位移反应。设在径向(横向)的挡块,在一定程度上增加了横桥向的刚度,横桥向的内力反应有增大。
平面不规则的曲线桥,在地震作用下将产生弯扭耦合现象,挡块会使主梁的跨中扭矩增大,而墩底扭矩未见增加,反而中间墩有轻微减小,这主要是主梁在水平面内的扭转振动通过挡块让各墩共同分担,减轻了与主梁固接的中间墩的扭转负担。
文章采用非线性模态时程分析,选取的地震波有一定的特殊性,这是由时程分析本身的特点决定的,实际工程还需根据桥址的场地特征,作进一步的选波工作,以期分析结果更具有代表性。
SAP2000 的非线性模态时程分析(即FNA 快速非线性时程分析)只能考虑连接单元(缝单元GAP 等)的非线性属性,其他单元在整个分析过程中始终表现为线性,所以大震作用下设置了限位挡块的桥梁的非线性表现还有待进一步研究。
