PQCD 框架下γγ→M+M-(M=K,π)散射过程中波函数模型研究
2020-12-15程平
程平
(西南大学,重庆400715)
对于目前所面临的束缚态问题,使用Bethe-Salpeter 方程无法进行精确求解,在事迹具体得计算求解过程中只能用阶梯近似的方法。亦因为QCD 理论具有强耦合性质,所以我们求解时也不能用微扰计算。理论上Bethe-Salpeter 形式和量子化方法能确定强子的波函数,Bethe-Salpeter 方程的解是由非微扰贡献来决定,但无法得出准确的波函数。目前求解束缚态问题比较有用的一个方法是以近似束缚态解作为出发点建立波函数,BHL的强子波函数就是以近似束缚态的解得到的,但他获得的波函数的分布振幅与CZ 分布振幅明显不同,于是加入一个因子函数在BHL 函数中去获得类CZ 振幅,这个分布振幅除端点区域外与CZ 分布振幅基本相同,称之为强子价态波函数的唯象模型。现在一种能适应低能现象的强子光锥夸克模型也是较好的一种方法。
在计算γγ→π+π-,K+K-)散射截面的过程中,明确π 介子和K 介子的波函数是十分重要的一步。我们设计波函数的模型为

这个波函数模型中表示赝标介子的分布振幅
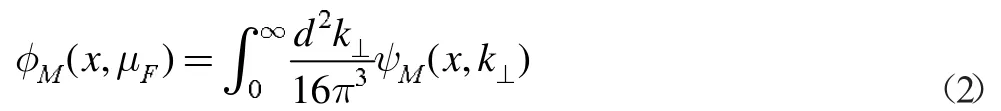
根据约束条件∫d2k⊥∑soft(t,k⊥)/16π3=1。通过介子的固有夸克产生软的横向动量,对横向动量的依赖被选择为一个较简单的高斯形式
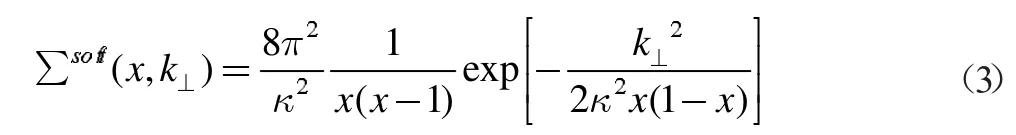
其中κ 是间隙参数,文献中常用的确定κ 的方法是计算介子的非微扰性质,并与这些量的实验测量值相比较,然而,由于实验测量值的不确定性,这个过程只允许一个约束参数κ在相对较大的范围内。我们对它进行求解,先定义均方根的横向动量的价夸克为
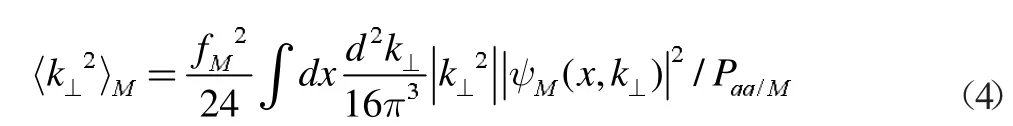
这里M=π 表示的是π 介子,M=K 表示的是K 介子,其中fM表示衰变常数,K 和π 介子的衰变常数分别为fK=0.160Gev和fπ=0.132Gev,Pqq/M介子的价态Fock 态的概率,Pqq领头阶Fock态几率在赝标介子中一般不大于1
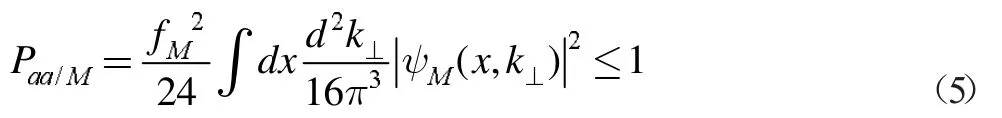
接着将(3)式代入(1)式,然后再将(1)式代入(5)式后可以解得
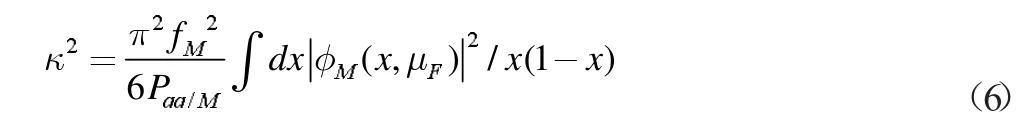
介子光前分布振幅Soft 部分可以将积分从k⊥到Q2截止得
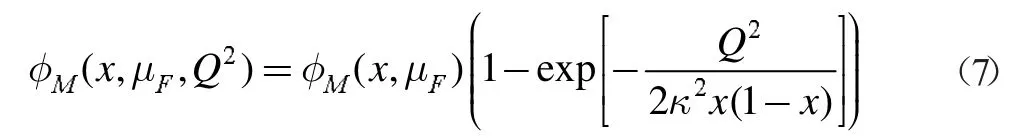
对于Soft 部分的指数因子,当Q2>1Gev 时贡献极小,基本为零,是可以忽略的,式(7)给出了软域中分布振幅的Q2依赖性的分解模型。
Q>1Gev 的情况下,我们就要考虑硬胶子的一个交换,它在分布振幅中提供额外对Q2的依赖,所以硬的部分分布振幅φM(x,μF)来自硬胶子交换的贡献,在考虑部分子质量时,取

mi是组分夸克质量,在式(8)里
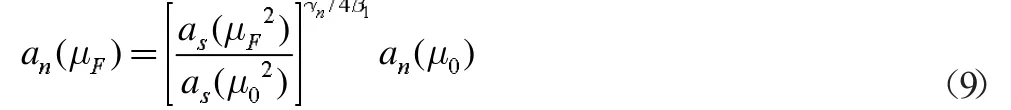
an(μ0)是分布振幅在初始标度μ0=1Gev 上的盖根保尔展开系数,从盖根保尔多项式的标准正态性出发有

αs(μF2)是跑动耦合常数。其中式(9)中γn是演化核的特征值
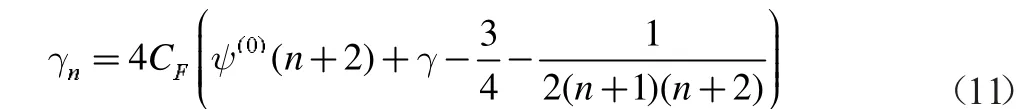
(1.8)式的N 应该满足归一化条件,所依N 由此来确定

在mHSA 中,由于波函数的卷积和硬散射振幅存在于横向动量的b 空间里,因此我们得用傅里叶变换把波函数变换到b空间里去

由此我们可以得出波函数的总模型如式(13)所示,Ψ(x,b,μF)表示的是赝标介子的波函数,φ(x,μF)表示的是分布振幅。
在确定低动量转移标度μ0~0.5-1GeV 下的赝标介子分布振幅方面已经做了许多工作,但这些研究大多集中在式(8)中的前几项,然而,由于演化分布振幅的收敛速度较慢,低标度上的介子分布振幅与其渐进形式可能存在显著差异,仅使用一种条件下的完整解会对研究造成很大的限制。于是本文中分布振幅用非微扰的方法来进行计算,除了用Ads 的形式进行研究外,还使用了其他几种模式来进行对比研究,其twist-2 分布振幅的模型列举如下
(a)Ads/QCD 形式

(b)渐近(asy)形式

(c)Chernyak-Zhitnitsky(CZ)形式

下面给出Ads,asy,CZ 模型的分布振幅
通过图(1),我们可以看到Chernyak-Zhitnitsky 模型在图中与Ads、asy 模型形状是不一样的,CZ 模型在x=0.5 时是为零的。
以上我们得到的波函数的总模型的主要优势在于指数因子可以有效压低x=0 和x=1 处的端点问题,消除端点的奇异性,从而使我们最后在计算散射截面时得到的数值结果可以更好的与实验上的数据吻合。除此之外,它在其他很多情况下,还具有很好的推广性。在本文中只给出了twist-2 部分分布振幅的几种模型,twist-3 部分没有进行讨论,可以在接下来的工作中继续讨论给出。

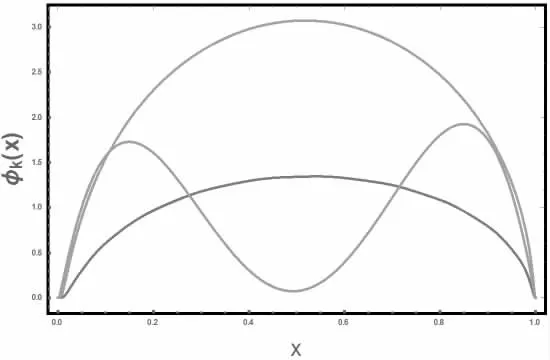
图1 π、K 介子的分布振幅模型,蓝、橙、绿色实线分别表示Ads、asy、CZ 形式
