致密油藏压裂水平井缝网系统评价方法<br/>——以准噶尔盆地吉木萨尔地区为例

致密油藏压裂水平井缝网系统评价方法
——以准噶尔盆地吉木萨尔地区为例

2020-12-15陈志明陈昊枢廖新维曾联波

石油与天然气地质 2020年6期

陈志明，陈昊枢，廖新维，曾联波，周彪

[中国石油大学(北京) 油气资源与探测国家重点实验室，北京 102249]

致密油藏渗透率极低，自然生产条件下不存在经济产能。为突破这一瓶颈，水平井大型压裂技术在致密油藏中应用越来越广泛[1-2]，是获取致密油经济产能的重要手段之一。为更高效地开发致密油藏，开展大型压裂水平井复杂缝网系统评价、反演缝网特征参数是一项非常重要的工作。

针对复杂缝网系统评价技术，目前主要方法为井间微地震监测技术。2002年，Fisher等[3]利用微地震监测技术评价了裂缝改造规模及缝网产状。利用地面和地下测量仪来获取微地震监测数据，然后通过分析微地震数据以确定体积压裂裂缝规模和特征，并详细地讨论了如何进一步矫正获得的裂缝网络参数。2008年，Mayerhofer等[4]认为在致密油气井在经过大型水力压裂后，井附近会形成复杂缝网，而此复杂缝网可视为一个三维改造区。同时，针对实际体积压裂井，基于微地震监测数据，建立三维改造区的数值模型，并利用历史拟合方法评价其裂缝网络参数。2009和2010年，Cipolla等[5-6]针对Barnett致密储层，利用分区表征方法将改造后的储层描述为压裂受效区和非压裂受效区。同时，将改造的复杂缝网细分为有支撑剂填充和无支撑剂填充的裂缝网络。2010年，Harikesavanallur[7]提出了一种体积裂缝模拟方法(VFMA)来描述压裂后的缝网，将整个地层分为3个区域：原始储层、压裂破碎区和压裂支撑剂填充区。改造区的裂缝网络利用双重介质来描述，并利用历史拟合方法获取不同区域的参数。2013年，Suliman[8]基于微地震监测数据对体积压裂产生的地层进行描述，由大到小分为3个区域：相关区、改造区和受效区。其中，相关区为微地震事件发生的所有关联区域；改造区即因体积压裂作用改造而使地层渗透率增加的区域；受效区即体积压裂井初始产量贡献区域，也就是体积压裂有效渗流区。2010年，Williams等[9]利用开始将Hough变换法[10]应用到微地震数据的裂缝识别中。受此启发，2016年，Yu等[11]利用Hough变换法对微地震监测数据进行裂缝识别。

井间微地震监测技术可获得以下信息：裂缝几何形态、裂缝复杂程度、裂缝位置及改造体积等[5-6]。但该方法缺少对裂缝渗透率、裂缝导流能力、有效裂缝半长及有效改造体积等参数的定量评价。曾联波等[12]学者指出大、中尺度裂缝对油气渗流起到重要作用，是影响油气井产能、空间流场和压力场分布等的重要因素。同时，任龙[13]采用流固耦合理论对致密油藏压裂水平井的产能进行了模拟，发现裂缝渗透率、导流能力、有效裂缝半长及有效改造体积等参数对压裂水平井产量具有极其重要的影响。虽然目前一些学者基于试井理论在裂缝参数反演方面取得了一些初步进展，但裂缝模型简单[14]，未考虑复杂裂缝网络特征和弱补给特征。因此，为更有效地对这些复杂裂缝井进行定量评价，本文基于致密油复杂渗流特征和裂缝网络复杂形态，考虑了非均匀缝网和弱补给等复杂因素，推导了其试井数学模型，提出了试井曲线拟合分析方法，并建立了致密油藏压裂水平井缝网系统评价方法。最后，为验证评价方法的可靠性，以准噶尔盆地吉木萨尔地区为例，开展了实例应用分析，为其参数反演和压裂评价提供技术支持。

1 复杂裂缝网络物理模型

1.1 物理模型建立

为模拟水平井的大型多段压裂情况(图1)，沿着水平井井筒建立了裂缝网络物理模型(图2)。考虑到大型压裂改造后，近井地层物性会发生变化，如流体粘度和渗透率发生改变，建立了储层非均质模型：①近井区域为渗透率较高的压裂改造区，含主裂缝和次级裂缝网络；②远井区域为渗透率较低的压裂受效区，不含裂缝网络；③未受压裂影响的原始储层，反映原始地层的渗透率、孔隙度等参数区域。同时，考虑到地质和工程因素影响，裂缝发育程度沿着井筒是非均匀的，建立裂缝网络的非均质模型。

图1 非均质缝网及储层特征的水平井大型压裂示意图[15]Fig.1 Schematic diagram showing massive fracturing of a horizontal well with nonhomogeneous fracture networks and reservoir properties[15]

图2 水平井裂缝网络系统物理模型Fig.2 Physical model of horizontal wells with complex fracture networks

1.2 模型假设条件

物理模型的基本假设条件如下：

1) 地层为上下封闭、均质、水平无限大；

2) 初始油藏压力假设为pi，渗透率假设为K，储层厚度假设为h，孔隙度为Φ；

3) 裂缝贯穿整个地层，忽略裂缝两端流动，裂缝网络为有限导流；

4) 微可压缩流体作等温、单相、达西渗流，并忽略流体垂向流动；

5) 油藏基质流体仅流向裂缝，不考虑储层流体向井筒供给；

6) 裂缝网络沿着井筒是非均匀的，相邻裂缝间裂缝网络视为均匀分布，并利用双孔介质模型表征；

7) 裂缝网络水平井以定产量qsc进行生产。

2 复杂裂缝网络试井数学模型

2.1 试井数学模型建立

根据水平井裂缝网络系统物理模型，储层流体的流动方式由远及近包括：原始储层的流体流动、压裂受效区的流体流动、压裂改造区基质和次裂缝网络的流体流动及主裂缝的流体流动。由于致密油藏原始储层渗透率极低，原始储层流体向压裂受效区的流动视作弱补给，利用混合边界考虑(图3)[16]。基于Brown和陈志明等的三线性流解析模型[14,17]，建立考虑弱补给效应下的非均质缝网及储层试井数学模型。

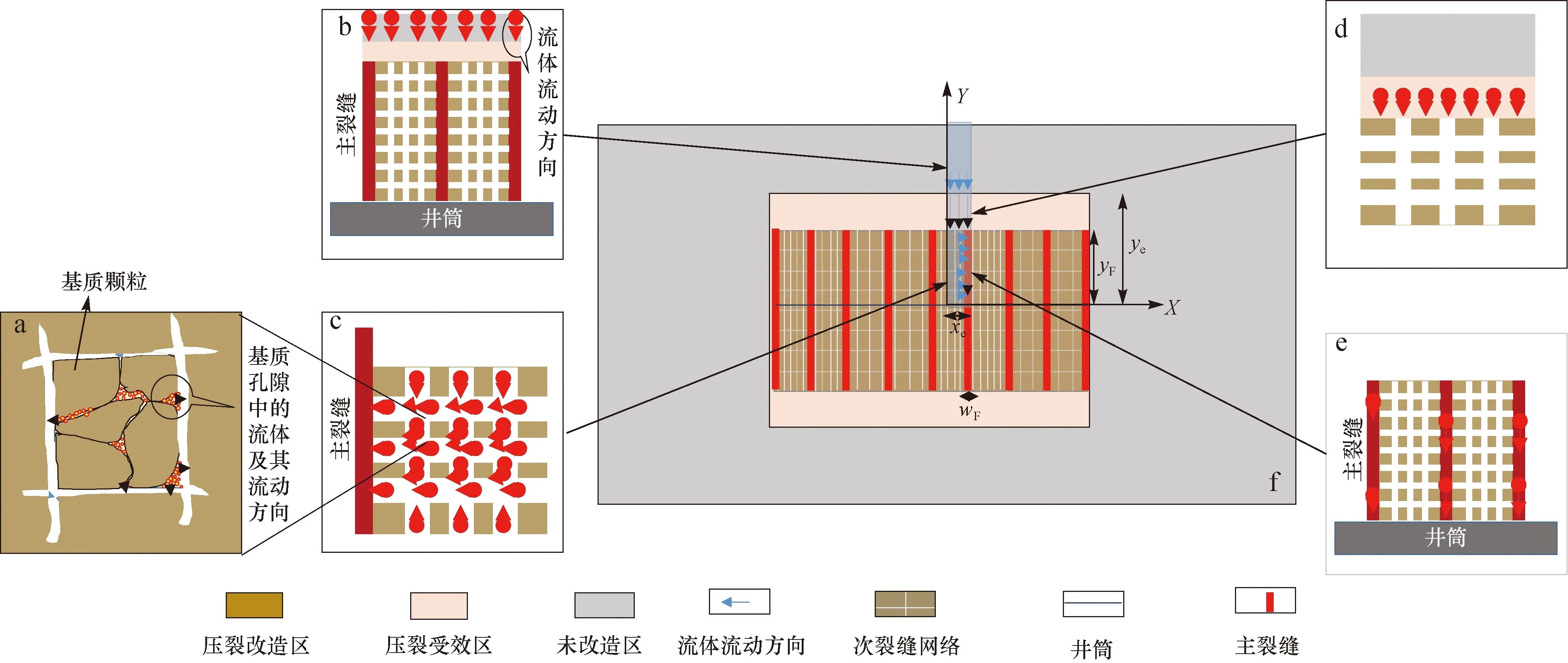
图3 考虑弱补给效应下的非均质缝网及储层流动示意图Fig.3 Schematic diagram showing the flow modes for nonhomogeneous reservoirs with fracture networks under weak fluid supplya.基质的流体窜流；b.原始储层的补给效应；c.次裂缝网络的流体渗流；d.压裂受效区流体渗流；e.主裂缝的流体；f.水平井裂缝网络系统物理模型

考虑到裂缝网络的非均匀特征，利用缝网离散的思路建立相应试井模型。假设主裂缝条数总数为n，针对主裂缝j，以其四分之一为研究对象，次裂缝网络的储容比和窜流系数分别为ωj,λj；主裂缝半长和导流能力分别为yFj,(KFwF)j。以此为基础，建立原始储层流体流动方程、压裂受效区流体流动方程、压裂改造区基质流体流动方程、压裂改造区次裂缝网络流体流动方程、主裂缝流体流动方程以及生产条件方程。

1) 原始储层流体流动方程

利用压降损失模型表征原始储层向压裂受效区的弱补给效应，即原始储层与压裂受效区交界面处压力变化可表达为：

(1)

式中：Sfs为补给表皮因子。基于渗透率的非均质变化，原始储层与压裂受效区交界面处流量变化可为：

(2)

将公式(2)代入公式(1)可得

(3)

式中：p2为压裂受效区压力；p3为原始储层压力，即为pi。因此，公式(3)可进一步表示为：

(4)

式中：

(5)

2)压裂受效区流体流动方程

在渗流过程中，压裂受效区流体满足连续性方程：

(6)

其中，运动方程为[12]：

(7)

利用渗透率指数模型表征储层应力敏感效应：

(8)

通过积分可得：

K=K2e-γ(pi-p)

(9)

将公式(7)和公式(9)代入公式(6)，结合岩石状态方程可得：

(10)

内边界条件为：

p2|y→yFj=pf1|y→yFj

(11)

式中：pf1为压裂改造区次裂缝网络系统的压力。压裂受效区外边界条件即为其与原始储层交界面处的条件方程：

(12)

初始条件为：

p2|t=0=pi

(13)

3) 压裂改造区基质流体流动方程

考虑到基质渗透率极低，忽略基质内部的渗流过程，仅考虑基质表面与次裂缝网络间的质量交换。利用Warren和Root模型[18]，可得到基质的流动方程：

(14)

将基质与次裂缝网络间的质量交换表征为拟稳态流动[13]，可得：

(15)

式中：pm为压裂改造区基质系统的压力。

4) 压裂改造区次裂缝网络流体流动方程

在渗流过程中，考虑到压裂改造区基质与次裂缝网络的质量交换和压裂受效区的流体流入，压裂改造区的次裂缝网络流体流动满足方程：

(16)

同样，类似公式(7)—(9)的推导方式，可得次裂缝网络流体满足方程：

(17)

其中：

(18)

(19)

内外边界的控制条件为：

(20)

初始条件为：

pf1|t=0=pi

(21)

5) 主裂缝流体流动方程

在渗流过程中，主裂缝流体满足连续性方程：

(22)

式中：

(23)

同样，类似公式(7)—(9)的推导方式，可得主裂缝流体满足方程：

(24)

内外边界的控制条件为：

(25)

初始条件为：

p|t=0=pi

(26)

式中：pF为主裂缝压力；qwj为主裂缝j流量。

6) 生产条件方程

考虑到裂缝网络水平井以定产量进行生产，得到生产条件方程：

(27)

2.2 试井数学模型求解

由上文可得，裂缝网络压裂水平的试井数学模型由公式(4)，(10)—(15)，(17)—(21)，(24)—(27)组成，为便于方程求解，先利用无因次变量简化模型后得无量纲数学模型。无因次变量为：

1) 无因次距离：

(28)

2) 无因次时间、流量和压力：

(29)

3) 改造区基质窜流系数和次裂缝网络储容比：

(30)

4) 无因次裂缝导流能力和内区导流能力：

(31)

5) 无因次裂缝扩散比和外区扩散比：

(32)

6) 无因次应力敏感系数和补给阻力系数：

(33)

利用无因次变量，简化试井数学模型公式(4)，(10)—(15)，(17)—(21)，(24)—(27)后得：

1) 原始储层和压裂受效区方程

(34)

2) 压裂改造区基质方程

(35)

3)压裂改造区次裂缝网络方程

(36)

4) 主裂缝方程

(37)

5) 生产条件方程

(38)

考虑到应力敏感造成的方程非线性，利用Pedrosa摄动变换方法[19]对无量纲试井数学模型进行线性化。首先，引入摄动变换方程为[19]：

(39)

将公式(39)代入无量纲试井数学模型后，利用零阶方程解可得到线性化后的试井数学模型。然后，利用Laplace变换方法对线性化后的试井数学模型进行求解，联立模型可得到井底压力解为：

(40)

其中：

(41)

利用Van Everdingen等[20]提出的叠加原理公式，考虑表皮效应和井筒储集效应下的井筒压力表达式如公式(42)。利用Stehfest数值反演算法[21]，对井筒压力解进行Laplace逆变换，得到实空间压力解。然后，利用公式(39)可得到考虑渗透率应力敏感条件下的井底压力解。

(42)

3 复杂裂缝网络试井模型结果

3.1 试井数学模型验证

为验证模型的可靠性，利用商业试井软件KAPPA[22]中三线性流模型进行验证。首先，建立复杂缝网水平井模型，模型中储层初始压力为30 MPa，厚度为10 m，孔隙度为0.1，水平井裂缝条数为30，其他参数见表1。考虑到三线性流模型不能考虑非均匀裂缝和弱补给效应，将新建模型进行简化，令βD→∞。从图4可看出，文中模型计算结果与商业试井软件KAPPA[15]结果基本吻合。

图4 复杂缝网水平井试井数学模型可靠性验证Fig.4 Verification on the reliability of well test model for horizontal wells with fracture networks

3.2 试井数学模型特征

基于上述模型，考虑原始储层的补给效应，对试井数学模型特征进行分析。由图5a中可看出，复杂缝网压裂水平井的井底压力特征曲线可分为7个阶段，包括：井筒储集和表皮效应、主裂缝双线性流、压裂改造区缝网系统中线性流、压裂改造区基质向缝网系统的流体窜流[23]、压裂受效区线性流、压裂受效区边界控制流和原始储层向压裂受效区的弱补给效应。其中，基质向缝网系统的流体窜流阶段，压裂导数曲线出现下凹；压裂受效区线性流阶段，压力导数曲线出现1/2斜率段；压裂受效区边界流阶段，压力导数曲线出现1斜率段；弱补给效应阶段，压力导数曲线下掉。这些模型特征可为缝网系统评价提供依据。

图5 不同缝网系统参数下试井模型理论双对数特征曲线Fig.5 Log-log plot showing the impacts of different parameters on the pressure transient behaviors of horizontal wells with fracture networksa.不同裂缝长度；b.不同裂缝导流能力；c.不同缝网储容比；d.不同窜流系数；e.不同敏感性系数；f.不同补给因子1.井筒储集和表皮效应；2.双线性流；3.压裂改造区线性流；4.流体窜流；5.压裂受效区线性流；6.边界控制流；7.弱补给效应

进一步对模型特征进行敏感性分析，分析主裂缝参数、次裂缝网络参数、渗透率应力敏感系数和补给阻力系数对试井曲线特征的影响。经过敏感性分析发现，主裂缝半长和导流能力主要影响裂缝双线性流和压裂改造区线性流阶段，随着主裂缝半长增大和导流能力下降，双线性流阶段时间越短，甚至会被掩盖。压裂改造区的次裂缝网络储容比及基质窜流系数主要影响下凹的深度和出现时间，反映基质向次裂缝网路的供油能力和速度。渗透率应力敏感系数和补给阻力系数对曲线后期影响明显，应力敏感系数越大，压降损失越大，曲线越往上翘。补给阻力系数越大，原始储层流体补给能力越差，越接近与封闭边界特征。因此，不同的改造效果和储层物性下，复杂缝网压裂水平井的试井曲线特征不同，这为通过压裂水平井试井资料评价缝网系统提供了理论基础。

4 实例应用

选取准噶尔盆地吉木萨尔地区一口致密油大型压裂水平井JHW，利用建立的缝网系统评价方法开展实例应用分析。JHW井是准噶尔盆地东部地区构造区域中芦草沟组上甜点体中一口井，位于吉木萨尔凹陷致密油层富集区JH井区(图6)，上甜点体储层孔隙度6.09%～25.79%，平均为10.99%，渗透率(0.001～0.284)×10-3μm2，平均为0.012×10-3μm2，渗透率小于0.1×10-3μm2样品占比90.9%，该油藏属典型的致密油储层[24-27]。目的层储层温度为82 ℃，原始地层压力约为37.6 MPa。该井于2016年11月4日在完钻，完钻井斜深4 145.00 m，完钻水平段长1 237.00 m。于2017年5月31日至6月10日，JHW井进行了多段多簇体积压裂。共压裂27段，平均段间距为43.7 m，27段中第1段射孔1簇3.0 m，第2—27段射孔3簇，每簇1.0 m，总射孔簇数为79。共注入压裂液为37 547.9 m3，总加砂量为2 475 m3。平均每段注入压裂液为1 390.7 m3，加砂为91.9 m3。井口破裂压力平均为67.5 MPa，停泵压力平均为40.2MPa。在压裂过程中，通过分析微地震数据发现沿着井筒方向分布着复杂裂缝网络。

图6 准噶尔盆地东部地区构造区域[28]Fig.6 Tectonic zones in the eastern part of the Junggar Basin[28]a.吉木萨尔凹陷位置；b.盆地东部地区构造① 沙奇凸起；② 五彩湾凹陷；③ 帐北断褶带；④ 石数沟凹陷；⑤ 黄草湖凸起；⑥ 石钱滩凹陷；⑦ 黑山凹陷；⑧ 梧桐窝子凹陷；⑨ 北三台凸起；⑩ 吉木萨尔凹陷；古西凸起；古城凹陷；古东凸起；木垒凹陷；南缘山前断褶带；阜康凹陷；白家海子凹陷；东道海子凹陷；克拉美丽造山带；博格达构造带

4.1 试井曲线拟合

由前文可知，通过压裂水平井的试井资料，可对裂缝网络系统进行评价。因此，为了评价JHW压裂水平井的裂缝网络系统，利用文中建立的复杂裂缝网络试井数学模型对JHW井试井测试数据进行试井曲线拟合分析评价，利用不断调参的方法，获得最佳的缝网系统拟合参数。图7为JHW压裂水平井的试井曲线拟合分析图，表2为JHW压裂水平井储层、井筒和缝网系统参数评价表。

表2 准噶尔盆地吉木萨尔地区JHW压裂水平井储层和缝网系统参数Table 2 Parameters of fractured networks and reservoirs in Well JHW of the Jimusar area in the Junggar Basin

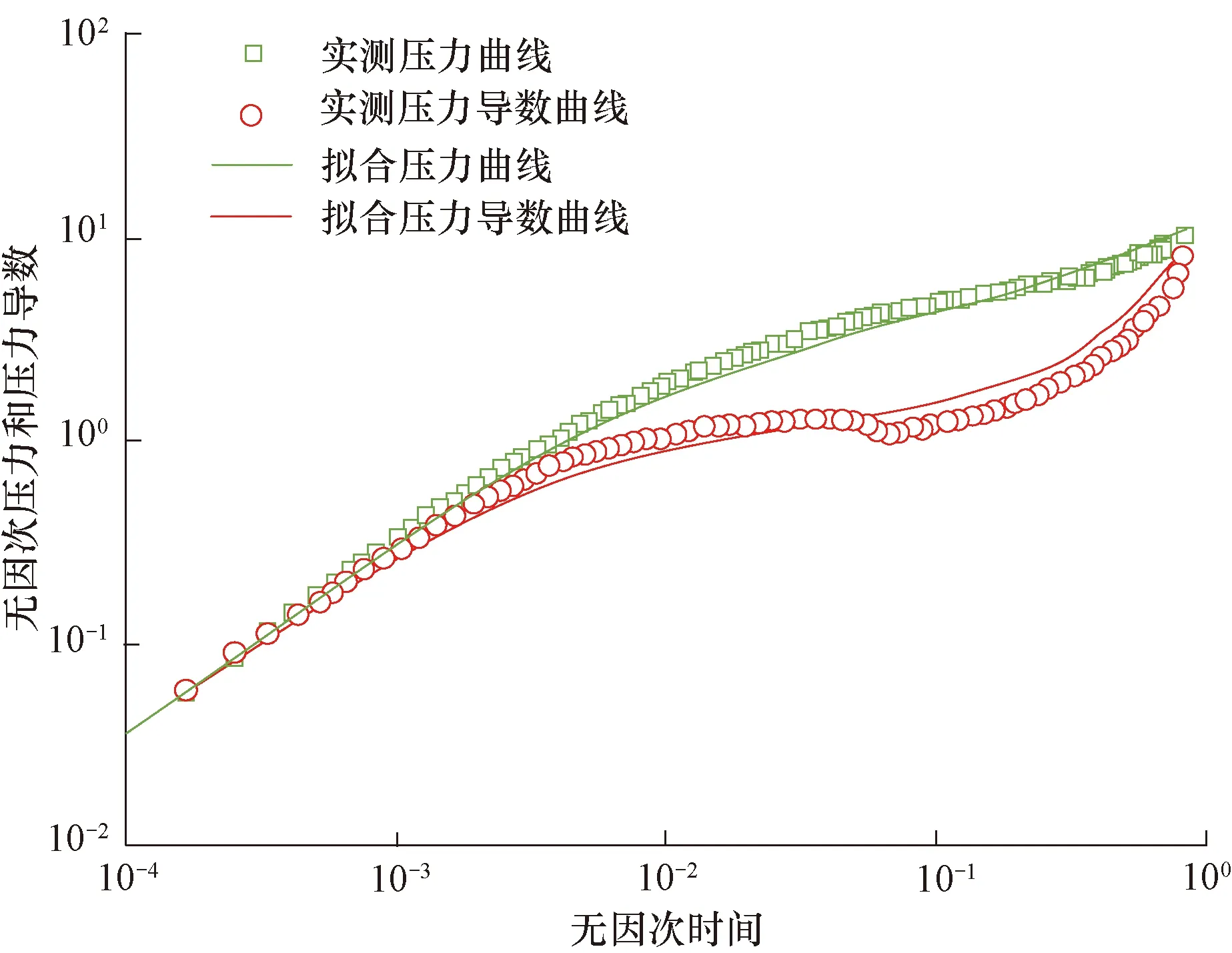
图7 准噶尔盆地吉木萨尔地区JHW井试井曲线拟合分析曲线Fig.7 Fitting curves of testing in Well JHW in the Jimusar area in the Junggar Basin

4.2 试井曲线拟合结果验证

利用所评价的储层和复杂缝网参数结果进行压力和产量耦合分析，以检验JHW井结果的可靠性。图8中理论曲线和实际曲线对比结果表明，曲线吻合程度较高，证明了JHW压裂水平井缝网系统参数评价较可靠。

图8 准噶尔盆地吉木萨尔地区JHW压裂水平井缝网系统参数评价验证Fig.8 Evaluation of fracture-network parameters along fractured horizontal Well JHW in Jimusar area of the Junggar Basina.日产油量和累积产油量拟合；b.压力拟合

4.3 裂缝网络系统评价

裂缝网络系统评价结果表明，经过大型压裂改造后，JHW井附近形成了主裂缝和压裂改造区，分布在水平井两翼，压裂改造区半宽为335.54 m。压裂改造区由基质和次裂缝网络构成，类似于双重孔隙介质，次裂缝网起流体渗流通道作用，基质起流体供给作用。次裂缝网络储容比为6.30%～17.99%，压裂改造区渗透率为100.8×10-3μm2。主裂缝为有限导流两翼缝，裂缝半长为135 m，导流能力为118.87×10-3μm2·m。

5 结论

1) 推导了含原始储层、压裂受效区和压裂改造区主裂缝及次裂缝网络的试井数学模型，考虑了非均匀缝网和弱补给等复杂因素。文中试井数学模型结果与商业试井软件结果基本吻合，可靠性得到验证。

2) 复杂缝网压裂水平井的井底压力特征曲线可分为7个阶段，包括：井筒储集和表皮效应、主裂缝双线性流、压裂改造区缝网系统中线性流、压裂改造区基质向缝网系统的流体窜流、压裂受效区线性流、压裂受效区边界控制流和原始储层向压裂受效区的弱补给效应。

3) 主裂缝半长和导流能力主要影响裂缝双线性流和压裂改造区线性流阶段。压裂改造区的次裂缝网络储容比及基质窜流系数主要影响下凹的深度和出现时间，反映基质向次裂缝网路的供油能力和速度。渗透率应力敏感系数和补给阻力系数对曲线后期影响明显，补给阻力系数越大，原始储层流体补给能力越差，越接近与封闭边界特征，为通过井底压力特征评价缝网系统提供了理论基础。

4) 裂缝网络系统评价结果表明，经过大型压裂改造后，JHW井附近形成了主裂缝和压裂改造区，分布在水平井两翼，压裂改造区半宽为335.54 m。次裂缝网络储容比为6.09% ～ 17.99%，压裂改造区渗透率为100.8×10-3μm2。主裂缝为有限导流两翼缝，裂缝半长为135 m，导流能力为118.87×10-3μm2·m。

符号说明

B—流体体积系数，m3/m3；

Ct—综合压缩系数，MPa-1；

CFD—主裂缝的导流能力，无因次；

RCD—压裂改造区的导流能力，无因次；

h—厚度，m；

Kf1—压裂改造区次裂缝网络渗透率，μm2(f1为压裂改造区次裂缝网络系统参数)；

Km—基质渗透率，μm2(m为基质系统参数)；

K2—压裂受效区渗透率，μm2；

K3—原始储层区渗透率，μm2；

KF—主裂缝渗透率，μm2(F为主裂缝压力系统参数)；

KFwF—主裂缝导流能力，μm2·m；