基于遗传算法的平面交叉口信号配时优化

陆颖　林丽

摘 要：为了提高平面交叉口的运行效率，以平面交叉口为研究对象，建立交叉口信号配时参数优化的非线性模型，该模型以交叉口的平均延误值最小为目标，约束条件为有效绿灯时间和周期时长，并采用浮点数编码遗传算法在Matlab软件中对信号配时参数优化模型进行求解。为验证优化模型的正确性和遗传算法的有效性，选取江苏省盐城市某一交叉口为算例，采用遗传算法对该模型进行求解。结果显示，优化后的平面交叉口的周期时长从123 s下降到97 s，下降率为21.1%;平均延误从32.79 s下降到14.91 s，下降率为54.5%;平面交叉口的服务水平从C等级上升到B等级。最后通过Vissim仿真对算例进行进一步验证，结果表明平面交叉口平均延误值下降幅度为24.1%。故遗传算法适用于平面交叉口信号配时方案优化，并且具有一定的可靠性与优越性。

关键词：平面交叉口;信号配时;平均延误;非线性模型;遗传算法

中图分类号：U491.51    文献标识码：A   文章编号：1006-8023（2020）06-0103-07

Signal Timing Optimization of Intersections Based on Genetic Algorithm

LU Ying，LIN Li*

（College of Automobile and Traffic Engineering， Nanjing Forestry University， Nanjing 210037， China）

Abstract：In order to improve the operation efficiency of a plane intersection， a nonlinear model for the optimization of the signal timing parameters of a plane intersection was established with the intersection as the research object. The goal of the model was to minimize the average delay value of the intersection， and the constraints are the effective green light time and cycle time. The model was solved by using the floating-point coding genetic algorithm in Matrix Laboratory software. In order to verify the correctness of the optimization model and the effectiveness of genetic algorithm， an intersection in Yancheng city of Jiangsu Province was selected as an example， and the model was solved by genetic algorithm. The results showed that the cycle time of the intersection after optimization decreased from 123 s to 97 s， with a decrease rate of 21.1%; the average delay decreased from 32.79 s to 14.91 s， the decline rate was 54.5%; the service level of intersections increased from C level to B level. At last， the example was further verified by VISSIM simulation. The result showed that the average delay value of the intersection decreased by 24.1%. Therefore， the genetic algorithm was suitable for the optimization of the signal timing scheme of the intersection， and had certain reliability and superiority.

Keywords：Plane intersection; signal timing; average delay; nonlinear model; genetic algorithm

收稿日期：2020-05-10

基金项目：住房城乡建设部2014年科學技术计划项目（2014-k5-007）

第一作者简介：陆颖，硕士研究生。研究方向：交通运输规划与管理，E-mail：1124065472@qq.com

通信作者：林丽，硕士，副教授。研究方向：交通运输规划与管理，E-mail：LinLi401@njfu.com.cn

引文格式：陆颖，林丽.基于遗传算法的平面交叉口信号配时优化[J].森林工程，2020，36（6）：103-109.

LU Y， LIN L. Signal timing optimization of intersections based on genetic algorithm[J]. Forest Engineering，2020，36（6）：103-109.

0 引言

国家经济的迅猛发展导致城市用地规模不断扩张，城市道路是城市的筋脉，而平面交叉口是城市道路交通的重要组成部分，同时也是城市道路交通的“堵点”所在[1]。因此，对平面交叉口的研究与治理将一直持续，其中对平面交叉口交通控制方面进行改善不失为一种有效方法[2]。其中对信号配时进行优化，不需要对平面交叉口的空间资源进行大规模改扩建，是一种成本低、见效快的有效方式。但是，目前许多城市道路信号配时方案还是根据经典Webster法进行求解，计算所求得的有效绿灯时间运用到交通流中产生的延误值往往较大，并会出现进口道的时间损失，浪费平面交叉口的时间和空间资源。

相比较经典的Webster法，智能优化算法具有一定的先进性，国内外大量学者将各种优化算法应用到智能交通控制领域中，在理论研究方面取得了较多的成果。Rouphail等[3]提出基于信号配时优化的CORSIM模型，通过遗传算法对模型进行求解，以网络延误和排队时间为评价指标。Kim等[4]提出利用遗传算法自动确定模糊控制交通系统中的最优参数和隶属函数，并且通过多个平面交叉口仿真验证了该方法的有效性。高云峰等[5]根据延误、停车率和排队长度3个优化指标，建立了基于非支配排序遗传算法的交叉口信号配时多目标模型，但是算例结果显示平均停车率比Webster算法得出的数值要高，3个优化指标之间并不能达到平衡。伍尚昆等[6]将改进的蚁群算法运用到多目标信号配时优化模型中，并且通过交叉口平峰和高峰两个时段进行模型验证，但是在平峰阶段，经典的Webster算法得出的总延误时间最小。李振龙等[7]从车辆延误、排队长度和尾气排放量3个性能指标，建立了以平面交叉口的信号控制优化模型，并采用遗传算法进行求解。刘畅等[8]以各相位有效绿灯时间为自变量建立多目标信号配时优化模型，其中优化目标为平面交叉口人均延误和人均 CO 排放，并通过粒子群算法进行求解。姚志洪等[9]以累计排队车辆延误为基础，提出平面交叉口信号配时双目标模型即通行能力最大、平均延误最小，但是算例结果表明两者并不能同时达到预期效果，模型效益不能最大化。

总体来看，粒子群算法、蚁群算法和遗传算法在信号配时参数计算中运用较为广泛，但是对于研究非线性规划模型求解问题，粒子群算法[10]在收敛性分析方面较薄弱，而遗传算法不仅拥有成熟的收敛性分析方法，并且能够估计收敛速度，蚁群算法[11]适合求解图中搜索路径问题，计算开销大，而遗传算法在选择操作时将会淘汰一些较差的种群，从而减少之后的计算开销。相比较于传统的遗传算法在编码阶段通常使用二进制编码，而二进制编码并不适合求解多维、高精度的连续函数优化问题，而浮点数编码不仅适合求解高精度函数问题，并且能够提高运算效率。因此，本文以平面交叉口平均延误最小为目标，建立非线性规划模型，采用浮点数编码遗传算法进行求解。该算法可通过常规软件进行操作，可广泛应用于交叉口信号配时优化工作，实用性强。

1 建立信号配时优化模型

平均延误、通行能力、饱和度、最大排队长度、平均停车次数、停车率以及油耗等通常作为交通效益评价的指标[12]。其中平均延误的大小可以最直观的体现平面交叉口的运行效率，故本文选取平均延误最小值作为目标函数。

1.1平均延误

平面交叉口的延误时间是指车辆在拥堵情况下，通过交叉口所需时间与畅通行驶同样距离所需时间的差值[13]。本文依据HCM延误公式[12]，将延误分为均匀延误和随机附加延误进行计算，其计算公式为：

2 遗传算法

遗传算法（Genetic Algorithms，GA）是一种全局自适应概率搜索算法，以自然选择和基因遗传学原理作为基础，以生物进化优胜劣汰的自然选择机理和生物界繁衍进化的遗传机制作为指导思想[14]。

本文建立的信号配时优化非线性模型具有不规则、不连续的特点，遗传算法定义的适应度函数有很强的适应性，即便是非规则、非连续或是有噪音的情况下，也能找到全局最优解，因此遗传算法适合求解本文的信号配时优化模型。遗传算法的具体步骤如下。

（1）初始参数的设定。种群规模n、交叉概率Pc、变异概率Pm、进化代数t。

（2）染色体编码。本文选取浮点数编码方法，该方法可以克服二进制编码因优化问题的精度要求而导致编码串很长、搜索空间急剧扩大、计算量大且时间长的一系列问题。其中，个体的编码长度与其决策变量的位数相等。

（3）适应度函数。本文以各相位有效绿灯时间ge作为优化变量，以平均延误为优化目标函数dI，有必要将目标函数转换成最大化问题形式，且为函数值非负的适应度函数。本文要求解平面交叉口平均延误的最小值，为了满足适应度函数的条件，适应度函数DI和目标函数dI之间的对应关系需要被建立，本文以目标函数的倒数作为适应度函数，即：

DI=1dI。  （13）

（4）選择。选取轮盘赌法作为选择算子，该方法是一种有退还的随机选择策略。群体中的每个个体都是圆盘中扇形的一部分，扇形面积越大，个体的适应值就越高，该个体进入下一轮选择的概率也就越大。假设种群个体数目为N，个体i的适应度为Fi，则它被选中的概率为：

Pi=Fi∑Nj=1Fj。  （14）

（5）交叉。选择实数交叉法[15]，该方法是指两个基因个体通过线性组合产生两个新的个体，如第m个染色体am和第n个染色体an在j位的交叉操作方法为：

amj=amj（1-b）+anjb

anj=anj（1-b）+amjb。（15）

式中：b是区间[0，1]之间的随机数。

（6）变异。采用非均匀变异。第i个个体的第j个基因aij进行变异的操作方法为：

aij=aij+（aij-amax）f（t），r>0.5

aij+（amin-aij）f（t），r≤0.5。（16）

式中：amax是基因aij的上界;amin是基因aij的下界;f（t）=r2（1-t/T）2，r2是隨机数;t为当前迭代次数;T为最大进化次数，r为[0，1]区间的随机数。

（7）进化终止条件。设最大进化代数为T，当迭代次数满足t=T条件时，基于遗传算法的最优解为种群中适应度值最高的个体，最后进行个体解码工作，得到平面交叉口的信号配时优化方案[16]。

3 实例分析

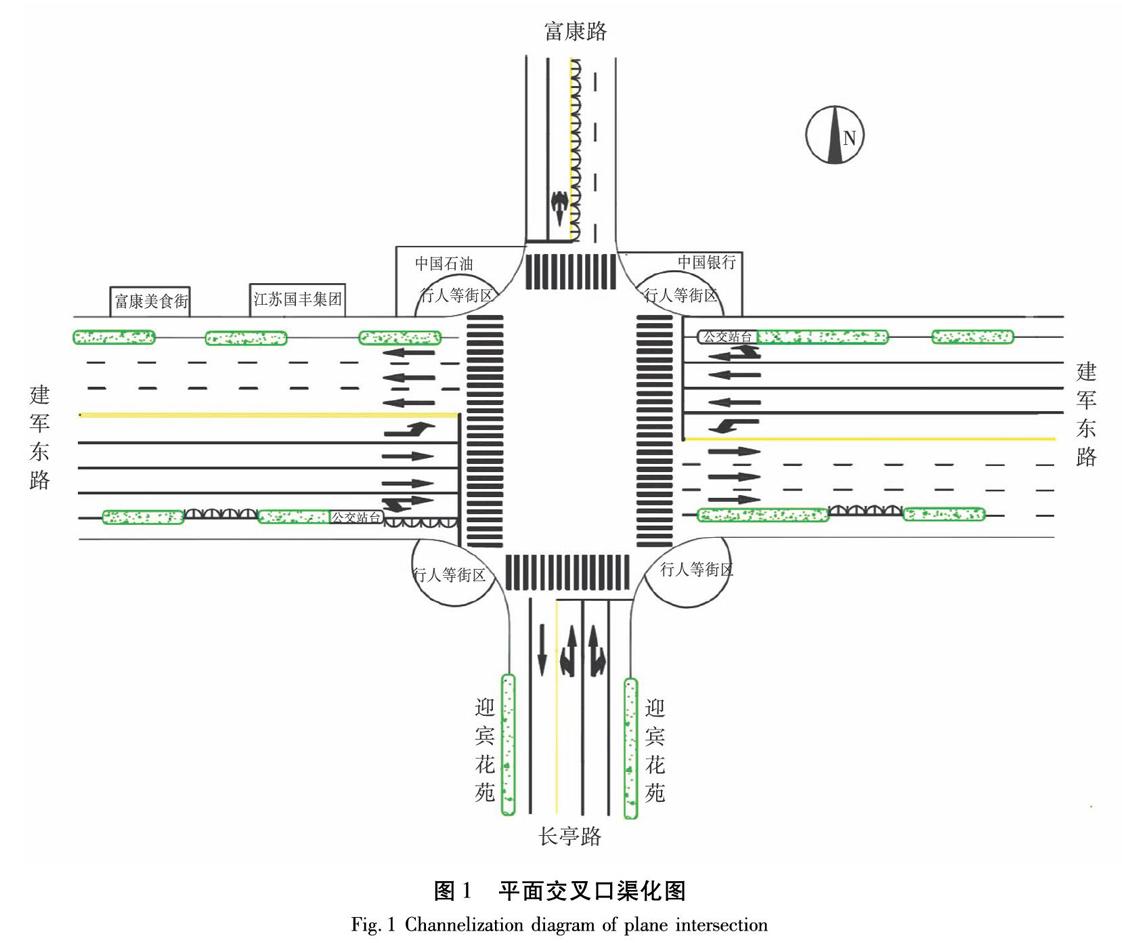
为了验证本文信号配时优化模型的正确性以及遗传算法求解的优越性，选取江苏省盐城市某一平面交叉口进行实地调查。该平面交叉口的几何构造和渠化方案如图1所示。该平面交叉口的交通控制方案为三相位，第一相位为东西进口道直行与右转车辆放行;第二相位为东西进口道左转车辆放行;第三相位为南北进口道左转、直行和右转车辆一起放行。经过多次调查发现，该平面交叉口的高峰小时出现在早上8：00—9：00，选取一天中的高峰小时对其进行高峰小时交通调查，并进行当量交通量的换算，最后调查结果见表1。

首先将现状交通量数据和配时参数运用Webster法重新进行配时计算，其次将本文建立的信号配时优化模型在Matlab环境下进行遗传算法求解。根据高峰小时周期时长推荐值[10]设置最小信号周期为40 s，最大信号周期为120 s;为了满足行人过街时长，设置第一相位最小有效绿灯时间为15 s，最大有效绿灯时间为60 s;第二相位最小有效绿灯时间为10 s，最大绿灯时间为50 s;第三相位最小有效绿灯时间为30 s，最大绿灯时间为60 s。

遗传算法中控制参数的选择也非常关键，通常这些参数包括种群规模n、交叉概率Pc、变异概率Pm和进化代数t。种群规模的大小会直接影响遗传算法的收敛性，推荐值为10～200，实例中取值为n=50;交叉概率控制着交叉操作被使用的频度，一般建议Pc的取值范围为0.4～0.99，实例中取值为Pc=0.6;变异概率控制着变异操作被使用的概率，一般建议值为0.000 1～0.1，实例中取值为Pm=0.01;进化代数t的一般取值为100～400，实例中取值为t=300。

确定各个控制参数后，将目标函数文件，选择、交叉及变异文件与算法主函数文件在同一文件夹下运行，在300次运行优化过程中，目标函数从120代开始收敛，即目标函数达到最优，运行结果见表2。从表2可知，周期时长从现状123 s下降到97 s，下降幅度为21.1%;平面交叉口的平均延误从现状32.79 s/pcu下降到14.91 s/pcu，下降率达54.5%;由遗传算法求解得出的信号配时如图2所示，第一相位的绿灯时间为46 s，第二相位的绿灯时间为11 s，第三相位绿灯时间为31 s。平面交叉口机动车延误与服务水平对应关系[17]见表3。由表3标准可知，现状交叉口平均延误为32.79 s/pcu，对应交叉口服务水平为C;Webster算法计算得出的平均延误对照表3，其交叉口服务水平依然为C;遗传算法得出的结果服务水平上升到B。Webster算法和遗传算法在一定程度上都使得现状交叉口的平均延误值得到下降，但从下降幅度来看遗传算法对信号配时优化模型的求解要优于现状以及经典的Webster算法，使得平面交叉口的平均延误进一步降低，服务水平从C等级上升到B等级，平面交叉口的运行效率随之提升。

为了进一步验证遗传算法的优越性，将现状、Webster算法以及遗传算法得出的配时方案在Vissim4.3中运行。根据表1平面交叉口当日高峰小时数据，按换算后的当量小汽车数据进行车辆输入，建军东路（即东西向）小汽车期望速度为40～60 km/h，富康路（即南北向）小汽车期望速度为20～40 km/h，分别对应相应的期望车速分布曲线;对平面交叉口各个进口道分别设置检测器对三项方案分别进行延误指标评价，仿真时长为3 600 s。仿真结果见表4。

根据表4中的仿真延误数据，总体来看大小顺序为：遗传算法得出的交叉口平均延误值、Webster算法延误值、现状延误值。从进口道延误来看，南、北进口增减量变化幅度最大，与现状平均延误值相比分别下降了17.5  s/pcu和18.5 s/pcu;东、西进口延误增减量幅度较小。从交叉口总体平均延误来看，基于遗传算法的平均延误值相比于现状值下降了5.6 s/pcu，下降幅度近似为24.1%;相比于Webster算法，下降了1.6 s/pcu，下降率幅度近似为8.3%。因此，基于遗传算法信号配时优化模型求解得出的平面交叉口平均延误值要低于Webster算法，可使平面交叉口平均延误值进一步降低，提高交叉口的运行效率。

4 结束语

信号配时参数的合理设置可以影响整个平面交叉口车流的畅通度，本文将平面交叉口的交通效益做出了量化评价，以平面交叉口平均延误值最小为目标函数，建立了以有效绿灯时间和周期时长作为约束条件的信号配时优化模型，通过浮点数编码遗传算法对模型进行求解，得出的结论如下。

（1）相比于现状和Webster算法，遗传算法求解得出的配时方案运用于平面交叉口，可使得交叉口的平均延误进一步降低，并且使得平面交叉口的服务水平上升到B等级，同时通过Vissim4.3仿真实验进一步验证了遗传算法对平面交叉口信号配时算法的适用性。

（2）本文的信号配时优化模型广泛适用于城市道路的平面交叉口，并且遗传算法的求解过程也可通过常规软件进行操作，实用性强，效果明显。

对于本文建立的信号配时优化模型，后续研究中可加入最大排队长度、通行能力等指标，建立多目标信号配时优化模型，从而更全面地評价平面交叉口的交通效益。

【参 考 文 献】

[1]成卫，袁满荣，姬利娜.基于粒子群算法的道路交叉口信号配时优化模型：以昆明市为例[J].城市交通，2013，11（3）：27-33.

CHENG W， YUAN M R， JI L N. Signal timing model based on particle swarm optimization： a case study of Kunming[J]. Urban Transport of China， 2013， 11（3）： 27-33.

[2]田丰，边婷婷.基于自适应遗传算法的交通信号配时优化[J].计算机仿真，2010，27（6）：305-308.

TIAN F， BIAN T T. Traffic signal timing optimization based on adaptive genetic algorithm[J]. Computer Simulation， 2010， 27（6）： 305-308.

[3]ROUPHAIL N M， PARK B B， SACKS J. Direct signal timing optimization： Strategy development and results[C]// In XI Pan American Conference in Traffic and Transportation Engineering， 2000.

[4]KIM J， KIM B M， HUH N C. Genetic algorithm approach to generate rules and membership functions of fuzzy traffic controller[C]// 10th IEEE International Conference on Fuzzy Systems.（Cat. No. 01CH37297）， IEEE， Melbourne， Australia， 2001， 1： 525-528.

[5]高云峰，徐立鸿，胡华，等.交叉口定周期信号控制多目标优化方法[J].中国公路学报，2011，24（5）：82-88.

GAO Y F， XU L H， HU H， et al. Multi-objective optimization method for fixed-time signal control at intersection[J]. China Journal of Highway and Transport， 2011， 24（5）： 82-88.

[6]伍尚昆，陈翠宜，祝胜林.基于多种群蚁群算法的交叉路口信号配时优化[J].计算机应用与软件，2014，31（5）：83-88.

WU S K， CHEN C Y， ZHU S L. Timing optimisation for intersection signal based on multi-colony ant algorithm[J]. Computer Applications and Software， 2014， 31（5）： 83-88.

[7]李振龙，董文会，韩建龙，等.基于遗传算法的交叉口信号控制多目标优化[J].计算机应用，2016，36（S2）：82-84.

LI Z L， DONG W H， HAN J L， et al. Multi-object optimization for intersection signal control based on genetic algorithm[J]. Journal of Computer Applications， 2016， 36（S2）： 82-84.

[8]刘畅，魏丽英.考虑人均延误和人均排放的信号配时优化模型[J].哈尔滨工业大学学报，2018，50（9）：83-88.

LIU C， WEI L Y. Signal timing optimization model considering per capita delay and per capita emissions[J]. Journal of Harbin Institute of Technology， 2018， 50（9）： 83-88.

[9]姚志洪，蒋阳升，吴北川.基于休假排队理论的信号配时仿真优化模型[J].计算机仿真，2018，35（6）：156-159.

YAO Z H， JIANG Y S， WU B C. Traffic signal timing simulation optimization based on vacation queueing theory[J]. Computer Simulation， 2018， 35（6）： 156-159.

[10]首艳芳，徐建闽.信号交叉口多目标动态决策模型及其优化方法[J].公路交通科技，2012，29（11）：92-97.

SHOU Y F， XU J M. Multi-objective dynamic decision-making model of signalized intersection and its optimization method[J]. Journal of Highway and Transportation Research and Development， 2012， 29（11）： 92-97.

[11]肖业伟，黄辉先，王宸昊.基于蚁群算法的交叉路口多相位信号配时优化[J].计算机工程与应用，2008，44（19）：241-244.

XIAO Y W， HUANG H X， WANG C H. Multiphase traffic signal timing optimization of intersection based on ant colony algorithm[J]. Computer Engineering and Applications， 2008， 44（19）： 241-244.

[12]吴兵.交通管理与控制（5版）[M].北京：人民交通出版社，2015.

WU B. Traffic management and control（Fifth edition）[M]. Beijing： Peoples Traffic Press， 2015.

[13]慕飞飞，张惠珍.基于遗传算法的单点交叉口信号配时优化[J].上海理工大学学报，2015，37（6）：600-604.

MU F F， ZHANG H Z. Signal timing optimization at single-point intersection based on genetic algorithm[J]. Journal of University of Shanghai for Science and Technology， 2015， 37（6）： 600-604.

[14]卓金武， 王鸿钧. MATLAB数学建模方法与实践[M]. 北京： 北京航空航天大学出版社， 2018.

ZHUO J W， WANG H J. Mathematical modeling method and practice of MATLAB [M]. Beijing： Beijing University of Aeronautics & Astronautics Press， 2018.

[15]李硕，付珊，贺文，等.基于遗传算法的左转待行区交叉口信号配时优化研究[J].公路工程，2018，43（5）：131-137.

LI S， FU S， HE W， et al. Study on signal timing optimization of the intersection with left-turn waiting area based on genetic algorithm[J]. Highway Engineering， 2018， 43（5）： 131-137.

[16]王逸，姚志洪，蔣阳升，等.基于自适应遗传算法的双环信号配时优化模型[J].工业工程，2018，21（5）：72-80.

WANG Y， YAO Z H， JIANG Y S， et al. The dual-phase signal timing optimization model based on adaptive genetic algorithm[J]. Industrial Engineering Journal， 2018， 21（5）： 72-80.

[17]王秋平，谭学龙，张生瑞.城市单点交叉口信号配时优化[J].交通运输工程学报，2006，6（2）：60-64.

WANG Q P， TAN X L， ZHANG S R. Signal timing optimization of urban single-point intersections[J]. Journal of Traffic and Transportation Engineering， 2006， 6（2）： 60-64.