LSTM神经网络在股票价格预测中的应用
2020-12-14张晓春徐晓鹏魏苏林
张晓春 徐晓鹏 魏苏林


摘要:针对循环神经网络RNN预测方法在深层网络反向传导中易产生梯度爆炸、消失现象,研究了一种基于变长Batch策略的长短时记忆(LSTM)循环神经网络股票价格预测方法。首先,以股票历史时间序列数据为研究对象,构造不同天数长度的时间序列,作为网络的输入;然后训练过程中,加入Early-stopping技术,防止学习的过拟合;最后,用状态参数传递的方式利用变长Batch在测试集上对未来股票收盘价进行预测。通过与传统机器学习回归模型性能的比较,验证了基于变长Batch的LSTM预测模型及参数优选策略在股票价格分析中具有较好的泛化能力和较低的预测误差。
关键词:长短时记忆模型;循环神经网络;深度学习;时间序列;过拟合
中图分类号:TP389.1 文献标识码:A
文章编号:1009-3044(2020)28-0039-05
Abstract: This paper uses a varied batch LSTM technique to predict stock prices. The varied batch LSTM is designed to overcome gradient blow up or vanish. Firstly, build time series with different length for input, and then add Early-stopping method to avoid over-fitting during training stage. Finally, save state and change batch size for testing. Mean Squared Error is measured, and the model is compared to the logic regression model. The results suggest that the LSTM has better predictive power and low MSE, especially where using a strategy of ten days history data.
Key words: long short term memory; recurrent neural network; deep learning; time series;over-fitting
1引言
股票是一种动态、高噪声的时间序列数据。作为经济晴雨表的股票在一定程度上反映了国民经济的发展趋势。股票的预测是一项艰难而又富有挑战性的任务,一直以来备受包括金融、统计、计算机等领域研究学者的关注。
股票预测大致分为统计分析、机器学习、深度学习三类。早期的预测主要使用统计分析方法。由于股票价格作为一种时序数据,具有高噪声、非平稳性等特点,传统的统计分析方法经常难以拟合复杂非线性关系,并且预测精度不高[1-3]。近年来,随着机器学习理论及算法的快速发展,各种经典机器学习算法已被各领域专家、学者们成功地运用到股票的预测中,这些模型虽然可以建模股指历史数据和未来股票价格之间的非线性关系,但模型的泛化能力不足[4-7]。由于股票价格经常会受到各种因素的影响,采用深度神经网络可以通过学习大量数据,发现数据之间潜在的关系,并且具有良好的非线性逼近能力。在股票预测方面也取得了较好的效果。循环神经网络RNN已经广泛地应用到时序数据的预测中,但是对于超过10层的网络,RNN网络在反向传导的过程中容易出现梯度消失或爆炸的现象[8-9]。由于RNN受限于深层网络时序数据的应用,学者们又提出了LSTM模型,其在RNN基础上增加了遗忘门机制,有效地解决了梯度消失、梯度爆炸问题[10-11]。
LSTM神经网络在预测时序序列数据中极具优势。因此,本文结合目前前沿的LSTM优化技术,利用Early-stopping 技术防止过拟合问题[12],通过构造可变batch机制实现LSTM三层网络,并对TSLA股票指数进行实验,并取得较理想的预测误差。
2模型
2.1 线性回归
线性回归是一种最基本的机器学习算法,它通过数据建立模型,反映输入特征(独立变量)和目标(依赖变量)之间的关系,然后再用未使用过的数据进行预测。
Hochreiter等学者使用记忆门技术解决了RNN在深层网络反向求导过程中易造成梯度消失和梯度爆炸的现象[11]。LSTM模型对于诸如语音、信号、金融时序数据的训练、预测效果及运行时间等性能方面都有良好表现。
LSTM模型最重要的结构是由三个门构成:遗忘门ft决定哪些信息被该细胞过滤掉;输入门it决定哪些经过输入门的值用来更新记忆状态;输出门ot决定基于输入和细胞记忆的哪些部分被输出。公式2至公式5给出了标准LSTM结构的门控实现公式。ft首先通过读取当前时刻输入xt和上一时刻记忆单元状态信息ht-1,然后通过sigmoid函数输出0到1之间的值,结果用来选择有多少历史信息被保存下来。Wi、Wf和Wo表示权重,bi、bf和bo表示偏置信,Ct表示记忆单元,σ表示激活函数。
3实验与分析
3.1 数据集
本次实验数据采用特斯拉股票历史数据,包含TSLA股票2010年6月29日至2020年2月3日的10年历史交易数据,共计2416条日线数据。实验分为两部分,第一部分实验基于传统机器學习方法的逻辑回归模型,通过回归系数,分别选择单特征、多特征进行实验。第二部分基于不考虑特征工程的深度学习LSTM模型。
3.2性能指标
为了量化模型的预测效果,本文采用均方根误差MSE(Mean Squared Error)来表示。作为预测模型的评价指标,MSE是通过计算真实值与预测值之差的平方的期望获得,其值越小,表明预测效果越好。如公式(6)所示,[yi]表示真值,[yi]表示预测值,M表示测试样本总数。
3.3逻辑回归实验及分析
3.3.1 实验数据
第一组实验使用5个输入特征,分别是开盘价、最高价、最低价、收盘价和成交量,预测未来收盘价。为了评价回归模型预测能力,我们将数据分为两个部分,其中前80%,共1931条日数据作为训练集,而后485条数据作为测试集,用于评估模型预测能力。
3.3.2结果分析
表1给出了基于不同历史回看天数的逻辑回归预测MSE。从表1易见,历史回看天数虽然不同,但都在将前三天数据作为输入特征进行学习、预测时,获得最小的MSE。
选择最佳回看天数,可以通过比较不同回看天数的MSE变化曲线,如图3所示,根据前10天、15天、30天、50天、100天、150天等回看数据作为输入特征进行学习、预测,其MSE曲线都在3天时得到局部最小值,即针对该数据集,应采用前三天数据进行逻辑回归学习,回归后模型进行预测可以获得最小的MSE。
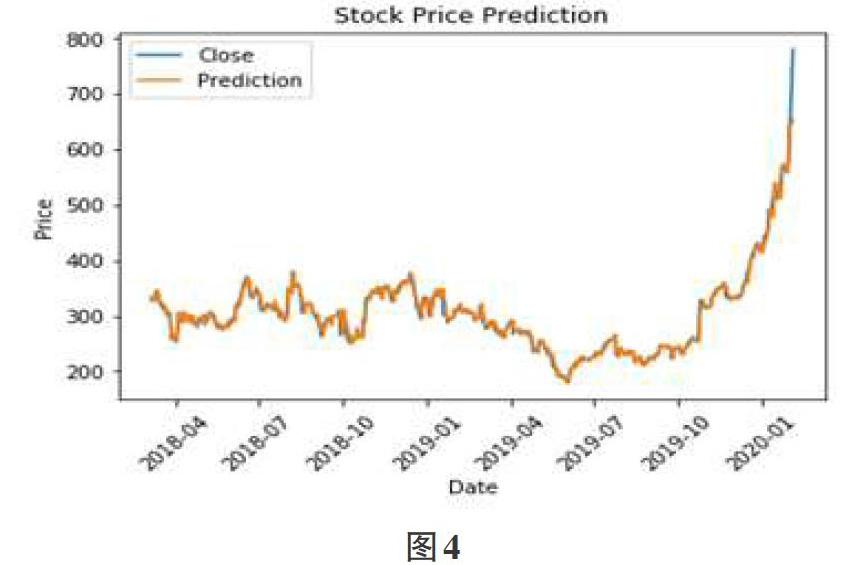
从MSE曲线得到了最佳回看天数为3,利用3个交易日的数据作为输入,未来1日收盘价作为输出,进行回归学习,回归后模型在测试集上进行预测,预测结果在整个测试集上,MSE为0.0011,准确率为:0.97,如图4所示。
3.4 LSTM实验及分析
3.4.1实验数据
本文采用了Keras进行时间序列LSTM 建模,相对于其他深度学习框架,Keras简单易用,而且后端支持Tensorflow,theano等框架。为了评价LSTM模型预测能力,我们将数据分为两个部分。其中前40%、20%日数据分别作为训练集和验证集,通过Early-stopping技术确定epoch次数。后20%日数据作为测试集,用于模型的预测。输入特征为开盘价、最高价、最低价、收盘价、调整后收盘价和成交量6个特征。另外,由于输入特征有不同的尺度,为了学习算法能够更快地收敛,我们在训练前调用scikit-learn的minmaxscaler函数将所有特征归一化到0和1之间。
本文针对股票时间序列数据,提出了一种基于可变batch的LSTM网络,包括一个输入层,一个含有10个神经元的隐含层和一个含有一个单元的输出层。LSTM单元使用默认的tanh激活函数,输出层使用一个线性激活函数。本文预测目标是股指未来收盘价,故选用均方误差MSE作为损失函数,采用Adam(Adaptive Moment Estimation)[12]优化器进行优化训练。
由于在训练神经网络时,batch size的大小直接影响梯度估计的准确性,所以权衡batch size和学习过程的速度及稳定性是尤为重要的。本文采用Mini-batch梯度下降方法訓练LSTM网络。在训练集和验证集上,batch size分别设置为8、16、32、64和128个样本大小,在测试集上,由于样本个数不能保证是训练batch size的整数倍,故在测试时,保留训练完成后模型的参数状态,重置batch size为1再进行预测。
3.4.2结果分析
表2给出了以历史60天数据构造的时间序列,共905个训练样本,X_train形状为(905, 6)和422个验证样本,X_valid形状为(422,6),y_train形状为(905, ),y_valid形状为(422, )作为网络输入进行学习。训练时batch_size分别设置为8、16、32、64、128,预测前,通过拷贝网络的权值,用训练后模型中的权值,重新创建一个网络,并设置其batch_size为1,再进行预测,解决训练和预测使用不同batch_size的问题。
图5至图9给出了基于历史60个交易日,在训练集设置不同batch_size的学习曲线(左图)和测试集上的预测值(Prediction)和真值(Close)曲线(右图)。
表3给出了以历史60天数据构造的时间序列,共935个训练样本,X_train形状为(935, 6)和452个验证样本,X_valid形状为(452, 6),y_train形状为(935, ),y_valid形状为(452, )作为网络输入进行学习。训练时batch_size分别设置为8、16、32、64、128,预测前,通过拷贝网络的权值,用训练后模型中的权值,重新创建一个网络,并设置其batch_size为1,再进行预测,解决训练和预测使用不同batch_size的问题。
图10至图14给出了基于历史30个交易日,在训练集设置不同batch_size的学习曲线(左图)和测试集上的预测值(Prediction)和真值(Close)曲线(右图)。
表4给出了以历史10天数据构造的时间序列,共955个训练样本,X_train形状为(955, 6)和472个验证样本,X_valid形状为(472, 6),y_train形状为(955, ),y_valid形状为(472, )作为网络输入进行学习。训练时batch_size分别设置为8、16、32、64、128,预测前,通过拷贝网络的权值,用训练后模型中的权值,重新创建一个网络,并设置其batch_size为1,再进行预测,解决训练和预测使用不同batch_size的问题。
图15至图19给出了基于历史10个交易日,在训练集设置不同batch_size的学习曲线(左图)和测试集上的预测值(Prediction)和真值(Close)曲线(右图)。
3.5 逻辑回归与LSTM的对比分析
比较表1和表2、表3、表4易见,逻辑回归在不同天数历史数据条件下,学习到的模型都可以达到较好的预测效果,并且MSE保持在0.0011左右。然而,LSTM模型在测试集上的预测效果浮动较大,MSE最低时达到0.000807,显著优于逻辑回归预测性能。LSTM网络的预测能力受网络深度、batch大小、样本大小、时间序列长度等参数的影响,本文实验在以历史10天数据预测第11天,学习阶段batch_size设置为8,测试阶段batch_size设置为1,得到了最低的MSE。实验结果也进一步说明了对于数据量不是很大的时序数据,用简单的机器学习方法也可以实现。而当数据量比较大,网络层次比较深,为了缓解过拟合、梯度爆炸、梯度消失的现象,选择LSTM构造深层网络是一种较好的选择。
4结论
本文研究了基于变长batch的 LSTM 神经网络模型,模型相比于传统逻辑回归模型具有更低的均方根误差MSE。基于目前的工作,在后续研究中可以在参数自动优化方面展开进一步研究,或者收集新闻等市场情绪因素,作为输入特征,以提高预测准确率。
参考文献:
[1] 于海姝,蔡吉花,夏红.ARIMA模型在股票价格预测中的应用[J].经济师,2015(11):156-157.
[2] Ariyo A A,Adewumi AO,Ayo CK.Stock price prediction using the ARIMA model[C]//2014 UKSim-AMSS 16th International Conference on Computer Modelling and Simulation.26-28 March2014,Cambridge,UK.IEEE,2014:106-112.
[3] 石佳,刘威,冯智超,等.基于ARIMA模型的股市价格规律分析与预测[J].统计学与应用,2020,9(1): 101-114.
[4] Patel J,Shah S,Thakkar P,etal.Predicting stock market index using fusion of machine learning techniques[J].Expert Systems with Applications,2015,42(4):2162-2172.
[5] Kumar D,Meghwani SS,Thakur M.Proximal support vector machine based hybrid prediction models for trend forecasting in financial markets[J].JournalofComputationalScience,2016,17:1-13.
[6] Singh N,Khalfay N,Soni V,et al.Stock prediction using machine learning a review paper[J].International Journal of Computer Applications,2017,163(5):36-43.
[7] Kim K J.Financial time series forecasting using support vector machines[J].Neurocomputing,2003,55(1/2):307-319.
[8] Samarawickrama A J P,FernandoTGI.A recurrent neural network approach in predicting daily stock prices an application to the Sri Lankanstockmarket[C]//2017 IEEE International Conference on Industrial and Information Systems (ICIIS).15-16 Dec.2017,Peradeniya,Sri Lanka.IEEE,2017:1-6.
[10] Liu, Y.; Guan, L.; Hou, C.; Han, H.; Liu, Z.; Sun, Y.; Zheng, M. Wind Power Short-Term Prediction Based on LSTM and Discrete Wavelet Transform[J]. Appl.Sci.2019,9:1108.
[11] Hochreiter, S.;Schmidhuber, J. Long short-term memory[J]. Neural Comput.1997, 9, 1735–1780.
[12] Kingma D P,Ba J Adam.A Method for Stochastic Optimization[A].International Conference on Learning Representations (ICLR)[C].2015(5) .
【通聯编辑:唐一东】