软件定义网络中基于模糊逻辑的实时路由更新

李雅波，姜丽芬，刘 涛，张 栋

（天津师范大学计算机与信息工程学院，天津 300387）

软件定义网络（software defined networking，SDN）是当今最热门的网络技术之一，SDN利用分层的思想，将控制平面和数据平面相分离，分别部署在独立的设备上实现[1].与传统网络技术相比，SDN有许多优点[1]：（1）控制平面统一控制转发平面上的网络设备，同时向上提供便捷的可编程操作；（2）网络运营商和第三方能根据自身需求开发新的控制方案，提供全新的网络应用和服务；（3）网络用户不必在意底层设备的技术细节，只需通过简洁的编程操作就能迅速达成目标应用的需求；（4）SDN可以提供灵活的网络资源管理和基于数据流的快速灵活的路由配置，能够自动优化网络资源的利用.因此，近年来SDN引起了学术界和工业界的广泛关注.

SDN需要周期性地进行路由更新，更新执行的速度是决定网络性能的关键[2]，更新执行越慢，传输过程中数据丢失和造成网络拥塞的可能性就越高.因此，路由更新是SDN的关键问题之一，众多学者对SDN路由更新方法进行了深入研究[2-15].其中：一类更新方法[2-3]预先设定了转发规则更新的次序，但这类方法很难适应实际数据量的动态特点；文献[4-5]提出根据当前数据流整体状况进行转发规则的更新，但随着执行更新的数据流逐渐增加，网络性能变差，实验分析表明[6]，只更新10 kB数据流，完成流表更新尚约80 s，而实际中等规模数据中心中数据流到达的速度约为1 250~1 667 B/s.文献[9]针对更新的带宽开销和交换机处理延迟等问题，提出基于通配符的请求成本优化流统计收集（CO-FSC）方案，该方案通过具有近似因子f的基于舍入的算法来降低带宽开销和交换机转发规则处理的延迟.文献[10]提出一种基于时间的更新实用方法，使用三态内容寻址存储器条目中的时间戳字段，来实现原子束更新，以高精度地协调网络更新.考虑到网络功能的随机性，文献[11]对基于马尔可夫链的路由更新算法进行了补充，在更新过程中，数据包通过选定路由的传输以比较所有可能的替代路由，实现了更新算法的虚拟化服务，并根据执行的算法为选择最佳路由提供建议.文献[12]首次提出了动态路由更新期间无缝保持一致性的方法，避免了频繁更新而导致数据包到达过程中出现明显的不规则延迟或“通信中断”.上述工作讨论了在路由更新中如何保持更新一致性及避免拥塞的问题，而没有考虑实时更新的问题.文献[13]探讨快速路由更新的问题，利用线性规划方法解决流的选取，其缺点是选择更新数据流时没有考虑当前链路的负载状况和公平性，造成数据流的选择不合理，并且线性规划算法执行速度较慢.文献[14]提出一种快速路由更新方法，适用于数据中心网络和广域网的更新，文献[15]提出了一种智能规则划分方法（SARD）来实现SDN中的快速更新，这2种方法的缺点是更新的数据流数量均较大，可能导致更新延迟过长.

本文提出一种基于模糊理论的数据流选择及路由更新策略（fuzzy quantified based flow selection and route update，FANS）.首先，使用语言量词和模糊量化命题确定各数据流相对于路由更新标准的符合程度，并结合链路可用容量决定更新的数据流，然后，利用链路容量和交换机存储容量限制寻找同步更新的数据流，进一步降低路由更新的延迟.仿真实验结果表明，本文的路由更新方法具有较优越的性能.

1 模型描述

1.1 网络模型

设网络结构为G=（S，L），S={s1，s2，…，sn}表示交换机构成的集合，L为链路集.路由更新的目的是将网络从状态C={f，Pc（f），f∈T}更新为状态C′={f，Pd（f），f∈T}，其中：T为进行路由更新的流的集合，C和C′分别为数据流的目前传输路径集合和目标传输路径集合，Pc（f）为流f更新之前的传输通路，Pd（f）为相应更新后的通路.假设每个数据流仅拥有一条传输通路.

交换机可以记录通过它的数据流，根据交换机的统计记录，控制器可以获知数据流的强度.但在实际情况中，数据流的强度可能会在空间和时间上呈现动态性，这种情况下控制器无法获知数据流的强度.文献[16]利用链路能够负载数据流的数量进行强度估计，链路容量为历史统计中能够一次通过的最大流数.本文中，若数据流的强度无法获知，则每隔一段时间记录该时间段内一次通过链路e的最大流数max（Tn，e）.设F（n）为当前通过链路e的最大流数，由指数加权平均法有

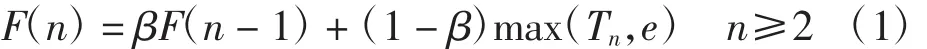
其中：F（n-1）为上一次统计中一次通过链路e的最大流数，β为权重.式（1）可写为

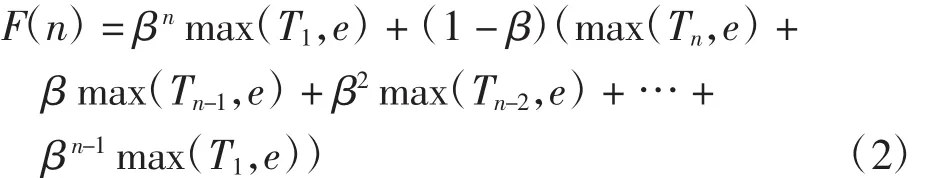
利用指数加权平均法预测最大流数，既考虑了历史状况，又考虑了网络当前的流量状态.优化算法中通常取 β≥0.9，此时有 β1/(1-β)≈1/e.由于越早的 max（Tn，e）权重越小，因此每次只需考虑最近1/（1-β）次的数据流最大个数的统计值，从而大大降低了交换机的存储代价.

1.2 延迟模型

设di为插入一个转发规则的时长，dm为修改一个流转发规则的时长.令d（s，Pc（f），Pd（f））为交换机s将流f从Pc（f）更新到Pd（f）的时长，且dm≈10 ms，di≈3.3 ms，则有

2 路由更新过程

2.1 更新数据流的选择

为满足路由的实时更新，利用人工智能的模糊理论确定各数据流相对于更新标准的符合程度.

2.1.1 模糊量词

令Q、X、A、B分别为模糊语言量词、论域和2个模糊谓词，模糊量化命题的形式为“Q XareA”或“Q B XareA”.相关研究表明[17-18]，模糊量化命题“Q XareA”适用于描述用户偏好.当Q为增量量词时，模糊量化命题“P：Q XareA”的真值TP是X的子集，

其中μA（x1）≥μA（x2）≥…≥μA（xn）.

2.1.2 基于模糊运算的路由更新排序及选择根据如下因素选择待更新数据流：

（1）数据流强度（flow intensity），即流数大小s（f）；

（2）数据流当前路由的负载（route load），定义为数据流当前路由上链路的最大负载，即其中H为链路带宽；

（3）数据流当前路由的拥塞程度（route congestion level），即负载较重的链路条数与总链路条数的比值；

（4）选择优先级（select priority），定义为某数据流在前m轮被选为待更新数据流的次数.

基于以上因素，每个数据流f被描述为一个具有4个对的集合{（cfk，ofk），k=1、2、3、4}，其中：cfk是流f的属性，of k为其具体取值.为选择待更新数据流，定义选择标准fselect，相应的，fselect具有 4 个对（cfk,pfk）,k=1、2、3、4,pfk为对于cfk的选择偏好.数据流f相对于选择标准fselect的符合程度（记为τ（fselect|f））是模糊量化命题“几乎所有的偏好都被满足”的真值.基于式（4），τ（fselect|f）的取值为

其中μp（cfs′）为数据流f的属性对选择偏好的符合程度,由模糊隶属函数求出,且μp（cf1′）≥μp（cf2′）≥…≥μp（cfm′）.各因素的模糊隶属函数见图1.

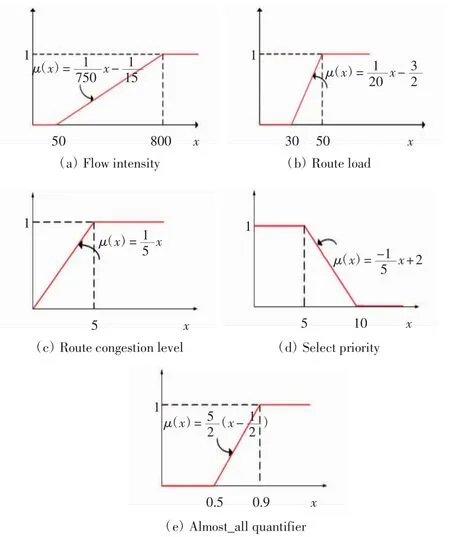
图1 模糊隶属函数Fig.1 Fuzzy membership functions

得到各数据流相对于选择标准的符合程度后,对于结果不为零的数据流,按照符合程度由大到小排列,形成序列Q.从序列Q的第1个流开始依次选择,对于流f的路径集Rf（所有可选路径的集合）内的各条传输路径,计算其上各链路的目前容量c（e）,进而得到传输路径P的目前容量C（P）为

从路径集Rf中选出容量最大的路径Pmax，由式（7）判断Pmax能否容纳f，若能则将f分配给路径Pmax.

其中λ为负载参量.上述路径分配算法的伪代码如下：

算法目标路径分配

2.2 同步更新数据流的挖掘

在保证链路无拥塞的前提下,控制器在相应的时间段内选择多个流同步更新,可以进一步降低路由更新的延迟.为此,在更新部分数据流的基础上,从链路容量限制和交换机流表容量限制2个方面进一步挖掘同步更新的数据流.

2.2.1 链路容量限制

链路容量限制保证同步更新数据流时链路无拥塞.对于Q中的流f，能够与该流同步更新的数据流满足

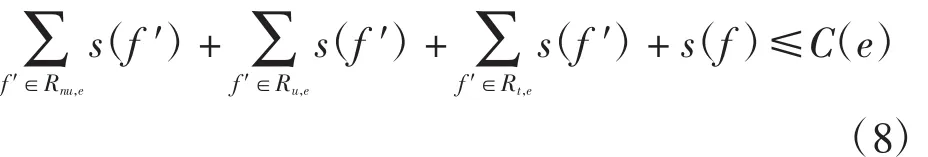
其中：Rnu，e为通过链路e且不需要更新路径的数据流集合，Ru，e为源路由通过链路e的数据流集合，Rt，e为目标路由通过链路e的数据流集合.

2.2.2 交换机流表容量限制

交换机流表容量限制保证在路由更新过程中交换机的流表大小不超过最大容量.设交换机s的流表容量为CP（s）,若更新后的路由通过交换机s，则其流表大小增加一个规则占用的空间rule（1）,其大小取决于openflow协议的版本号.设Rnu，s为源路由通过交换机s且暂不需要更新的数据流集合，Ru，s为源路由通过交换机s且需要更新的数据流集合，Rt，s为目标路由通过交换机s的数据流集合,则有

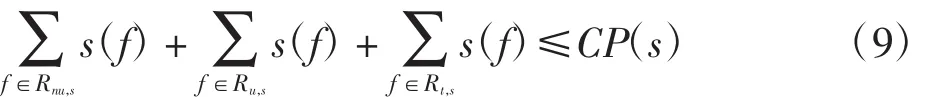
3 仿真实验与性能分析

3.1 实验环境

使用mininet生成网络拓扑,同时使用与文献[16]相同的网络拓扑生成工具，此生成工具是PSGen拓扑生成工具的一个修改版，能够模拟真实的大规模网络拓扑.实验网络拓扑包含25台交换机，100条链路，6 000个数据流，控制器选择Ryu.模拟的数据流遵循标准的2-8原则[19].实验中设β=0.9，λ=0.56.

采用2个性能指标评价路由更新算法的性能：（1）网络负载率（network load ratio），该指标用于衡量网络负载均衡度；（2）路由更新延迟（route update delay），即更新完成数据平面的总时间.

3.2 实验结果

将 FANS 与已有算法 EMCF+DS[16]、GRSU[16]和OSPF进行性能比较，本文设计了4组实验.

3.2.1 第1组实验

第1组实验考察当不同数量的数据流存在于网络中时，路由更新延迟和网络负载率的变化.

由于OSPF算法始终为数据流选择最短路径，所以这里不考虑它的更新延迟问题，图2给出了路由更新延迟随数据流数量的变化情况.

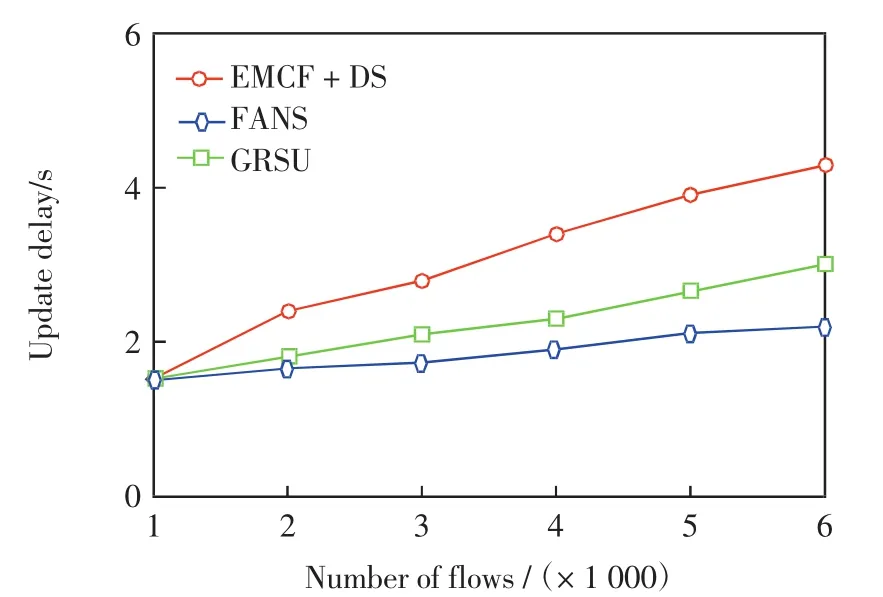
图2 数据流的数量对路由更新延迟Fig.2 Number of flows vs.route update delay

由图2可见，FANS的路由更新延迟要小于EMCF+DS和GRSU，当数据流数量为6 000时，FANS的路由更新延迟分别比EMCF+DS和GRSU低约2.1 s和0.8 s.EMCF+DS每次都要更新网络中的全部大象流，因此造成更新延迟较长，GRSU在更新流的选择时没有考虑数据流的强度以及选择的公平性等因素，导致更新效果略差.

图3给出了网络负载率随数据流数量的变化情况.由图3可见，FANS的网络负载率低于GRSU，略高于EMCF+DS，但FANS的更新延迟远低于EMCF+DS，综合考虑，FANS算法更具优势.另外，OSPF算法的网络负载率最高，当数据流数量为6 000时，其网络负载率约为0.7，这是因为数据流数量增大之后，某些主要链路的负载大大加重.

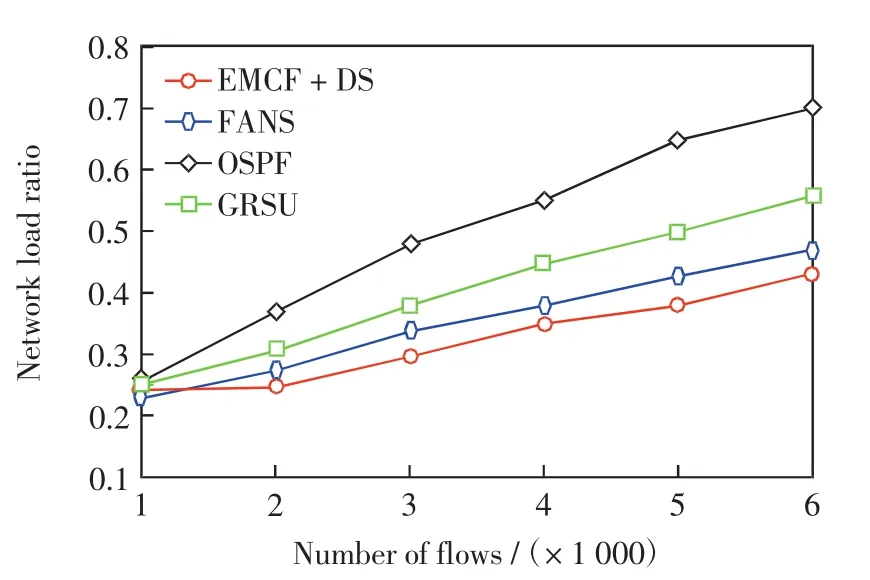
图3 数据流的数量对网络负载率Fig.3 Number of flows vs.network load ratio

3.2.2 第2组实验

第2组实验在第1组实验的基础上为FANS和GRSU设定一个最大更新延迟的阈值D0=1.5 s.因为GRSU为交换机设置了最大更新时延，另外当数据流量或网络规模较大时，实时更新可能无法保证，所以通过设定这样一个阈值来限制更新延迟.图4和图5分别给出了此时路由更新延迟和网络负载率随数据流数量的变化情况.

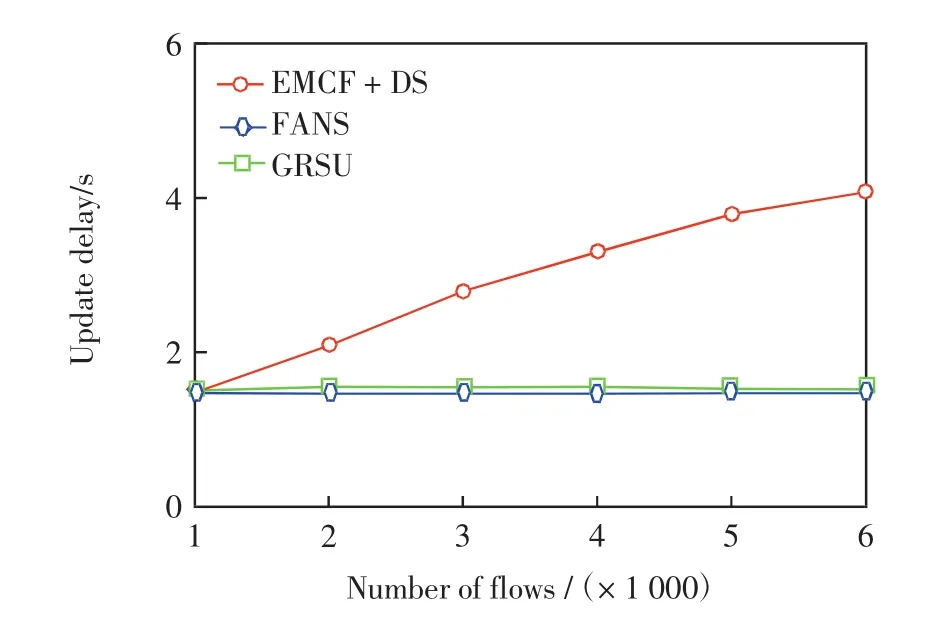
图4 数据流的数量对路由更新延迟（D0=1.5 s）Fig.4 Number of flows vs.route update delay（D0=1.5 s）

图5 数据流的数量对网络负载率（D0=1.5 s）Fig.5 Number of flows vs.network load ratio（D0=1.5 s）

由图4可见，由于设定了阈值，此时数据流数量的增大对FANS和GRSU的更新延迟没有影响，而EMCF+DS的更新延迟依然会随数据流数量的增大而增大.对比图5和图3，在设定阈值的情况下，FANS的网络负载率增大约5%，这是因为限定阈值后数据流较之前增多，能够更新的数据流数量比无设定时少，因此路由更新后的效果变差.由图4和图5可以看出，FANS的网络负载率稍高于EMCF+DS，但FANS的更新延迟却大大低于EMCF+DS.当数据流数量为4 000时，FANS的负载率比EMCF+DS高约5%，但其更新延迟比EMCF+DS低约1.8 s，当数据流数量为6 000时，FANS的更新延迟比EMCF+DS低约2.5 s，而负载率仅高约8%，说明FANS算法通过更新部分数据流，达到了负载率和更新延迟的平衡.

3.2.3 第3组实验

在第3组实验中，在默认函数基础上将大象流的门限进行扩大.当大象流的门限逐渐扩大时，图6和图7给出了路由更新延迟和网络负载率的变化情况.

由图6可见，随着大象流门限值成倍增加，FANS的更新延迟一直低于其他算法.由图7可见，随着大象流门限值增加，4种算法的负载率均不断增大，FANS的负载率仅高于EMCF+DS，当大象流门限为原来的4倍时，FANS的负载率比EMCF+DS高约5%，但更新延迟却低约2.5 s，因此FANS的性能更优.

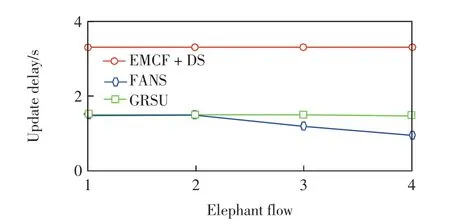
图6 大象流门限对路由更新延迟Fig.6 Elephant flow threshold vs.route update delay

图7 大象流门限对网络负载率Fig.7 Elephant flow threshold vs.network load ratio

3.2.4 第4组实验

在第4组实验中，固定数据流数量，考察最大更新延迟阈值D0对网络负载率的影响.图8（a）和（b）分别给出了当数据流数量为4 000和6 000时，网络负载率随D0的变化情况.

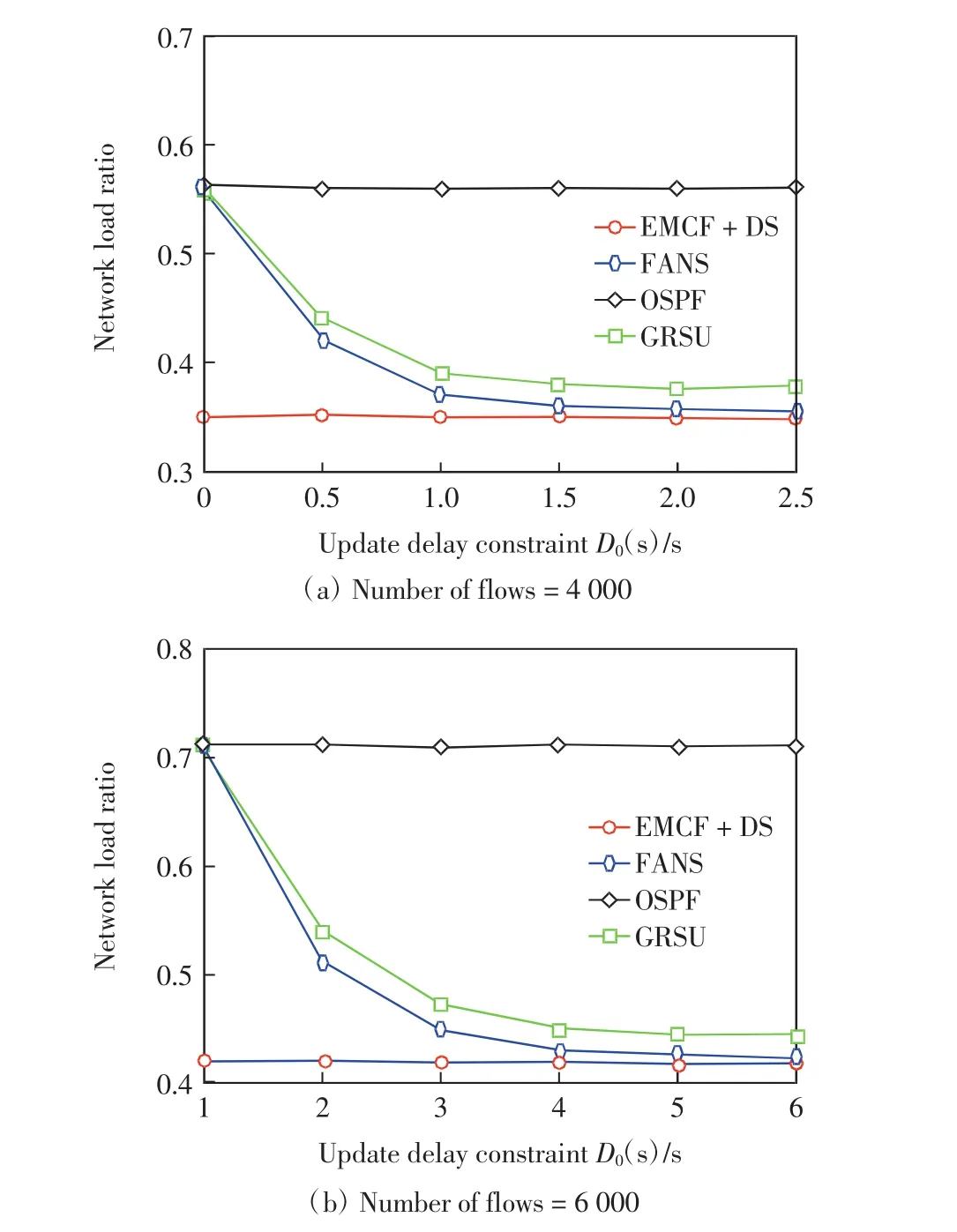
图8 最大更新延迟阈值对网络负载率Fig.8 Update delay constraint vs.network load ratio

由图8可见，随着D0的增大，FANS的负载率逐渐接近EMCF+DS，并且一直低于GRUS.但由于EMCF+DS需要更新全部大象流，因此其更新延迟会远大于FANS，另外，FANS采用了模糊逻辑，选择的数据流更加合理，因此负载率略低于GRSU.

3.2.5 负载参量λ对FANS性能的影响

数据流更新路径的选择与λ有关，因此FANS的性能受λ影响.图9给出了数据流数量为4 000和6 000时，不同λ值下FANS的网络负载率.由图9可见，λ=0.6时负载率最低.当λ从0.6缓慢增大时，网络负载率会逐渐增大，这是因为λ较大会导致一些主要链路负载较高，所以网络负载率也会增大.当λ较小时，链路容量没有得到充分利用，也会造成负载率较高.因此，选择合适的负载参量对路由更新算法的性能也很重要.

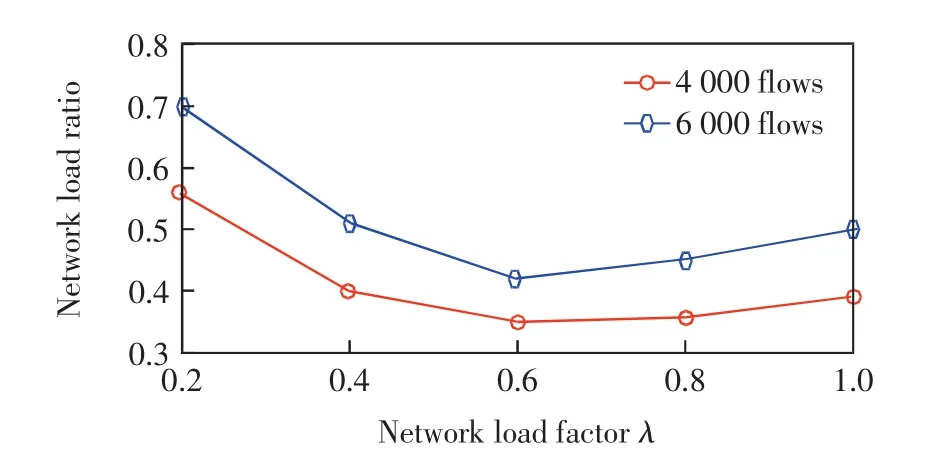
图9 负载参量对网络负载率Fig.9 Network load factor vs.network load ratio

4 结语

针对软件定义网络中的实时路由更新问题，本文利用人工智能算法的语言量词和模糊量化命题处理数据流的选择问题，同时考虑流的属性和各流相对选择标准的符合程度，尽量选择符合程度较高的数据流进行更新，这种策略可以保证在维持网络较小的更新延迟与开销的情况下，尽量降低网络负载率.仿真实验验证了本文所提路由更新方法具有较优越的性能.