考虑随机行程时间的电动汽车交通网络均衡

王晓一，潘义勇 （南京林业大学 汽车与交通工程学院，江苏 南京210037）

WANG Xiaoyi, PAN Yiyong (College of Automobile and Traffic Engineering, Nanjing Forestry University, Nanjing 210037, China)

0 引 言

随着交通技术的发展，电动汽车越来越普及，保有量也在逐年提升，电动汽车与普通燃油汽车的行驶行为存在较大差异，主要表现在电动汽车对电能的存储、充电设施的性能，以及充电时间和行驶里程的局限。现有的交通均衡分配模型大多是基于燃油汽车的出行方式而存在的，因此，研究针对电动汽车的交通网络均衡分配问题，对城市未来的交通规划、交通管理和环保问题等具有重要的现实意义和理论意义[1]。

Wardrop[2]首次提出用户均衡分配模型，但该模型没有考虑行程时间的随机性。Hong 等[3]针对随机行程时间提出了行程时间预算均衡模型，该模型是利用一定置信水平下的行程时间预算值作为交通网络均衡分配问题的目标函数。Chen 和许项东等针对随机行程时间提出了均值—超量交通均衡模型，并假设出行者以均值—超量旅行时间作为路径选择的准则[4-8]。温惠英等[9]提出的道路阻抗函数模型是根据行程时间波动性而建立的，采用了最大似然估计法对模型参数进行估计，并利用全有全无方法进行了实例的交通分配。以上是基于燃油汽车的出行方式提出的交通网络均衡分配模型，都考虑了行程时间的随机性。Fang[10-11]针对纯电动汽车提出了交通网络均衡模型，基于电动汽车能量消耗和充电时间制定数学模型解决路网流量分布。Adler 等[12]提出了里程焦虑，重新定义了电动汽车最短距离步行问题，并建立了以里程限制为约束条件的新模型。Liu 等[13]对涉及电动汽车的均衡交通分配问题进行讨论，获得最小化旅行成本。蔺靖军[14]通过对纯电动汽车充电桩的位置以及充电桩数量的限制，建立了一个考虑纯电动汽车驾驶行为的网络交通均衡模型。邓昌棉等[15]为了解决城市中电动出租车的充电需求，利用收集的出租车乘客讫点大数据，建立出了行驶距离最短的充电站选址优化模型。以上基于电动汽车的出行方式提出的交通网络均衡分配模型，考虑了电动汽车的充电时间，却忽略了行程时间随机性对交通出行的影响。

本文研究了同时考虑电动汽车随机行程时间和充电时间的交通网络均衡问题。首先，建立了考虑电动汽车随机行程时间和充电时间的交通网络均衡模型；其次，利用改进的Frank-Wolfe 算法求解上述模型；第三，针对Grid network 网络进行数值试验并对数值结果进行了分析；最后，总结了研究成果以及进一步研究的方向。

1 考虑电动汽车随机行程时间和充电时间的交通网络均衡模型

1.1 行程时间的随机性

考虑由有向图G（N,A）建模的交通网络，其中N是所有节点的集合，A是所有路段的集合。ca表示路段a（a∈A）的道路通行能力，xa表示路段a a∈（ ）

A的交通流量，网络用户均衡模型中的时间阻抗通过BPR 函数获得:式中：Ta表示路段a的行程时间；表示路段a自由行驶的时间；xa表示当时通过路段a的交通流量；ca表示路段a的道路通行能力；α、β 为模型的参数。

Hong 等[3]研究了路网中路段的通行能力ca是随机变量的情形，从而Ta也是随机变量，并假设通过路网中路段a的交通量xa与路段a的通行能力ca是相互没有关联性的，其期望值为：

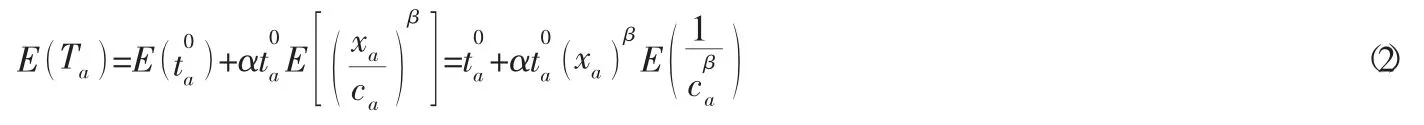
式中：E（）表示期望值。

假设ca是服从正态分布的，即对于正态分布的路段容量可以得到如下的期望值：

代入式（2） 中：

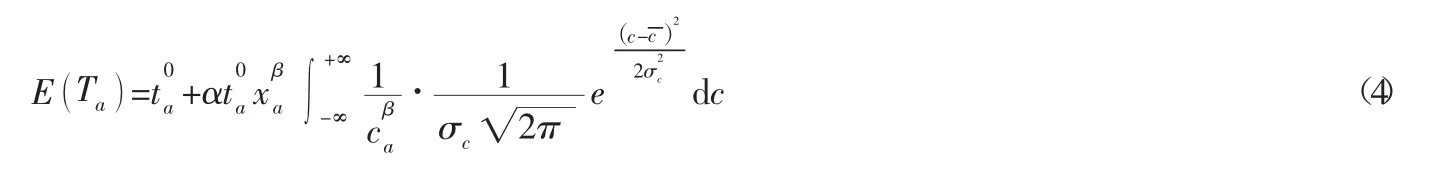
式中：N表示状态分布符号；～表示后者服从前者；表示服从正态分布时的均值；表示服从正态分布时的方差；σc表示服从正态分布时的标准差。

路线行程时间Tp可通过路段行程时间相加来表示：

式中：Tp表示通过路线所需要的总时间；a∈p表示行驶的路段a在路线p中。

1.2 改进的交通网络均衡问题

Liu 等[13]和蔺靖军[14]通过对电动汽车充电桩的位置以及充电桩数量的限制，建立了一个考虑纯电动汽车驾驶行为的网络交通均衡模型，但是没有考虑行程时间随机性，因此本文结合其模型和行程时间随机性建立了考虑随机行程时间和充电时间的交通网络均衡模型：

2 求解算法

Step 5：结束条件。利用前后两次迭代的流量变化情况来确定收敛条件，如果当前流量增量与更新后流量的比值低于指定阈值，则结束迭代；否则不满足收敛条件，令n=n+1，返回Step1 继续迭代。

此外，路径搜索本文采用的K短路算法，而不是笛卡尔最短路搜索算法。因为笛卡尔最短路找到的最优路径不一定能够满足充电汽车耗电的要求，所以出行最终的最短路是在所有可行路径中（采用K短路搜索算法） 筛选能够满足电动车耗电、充电需求的最短路径。

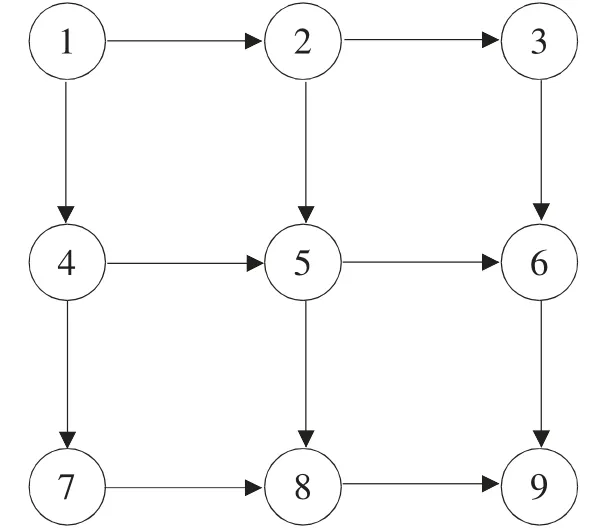
图1 Grid network

3 数值试验

3.1 Grid network

Grid network 是一个可扩展的网络，通常用于测试交通网络均衡分配问题。本文采用的Grid network（n= 3）包含9 个节点、12 条路段、1 对OD 对，如图1 所示，其中各个节点、各条路段属性见表1。

表1 网络属性

3.2 普通燃油汽车路网交通分配

设OD 对是节点1 和节点9，其之间的OD 流量为450（car），当道路网络中只考虑燃油汽车特性时，应用传统的交通均衡分配模型以及算法，得到的路段费用、路段流量、路径详细信息见表2 和表3，该路网总的行驶时间是102.034min。

表2 路网中都是燃油汽车时的路段费用及路段流量

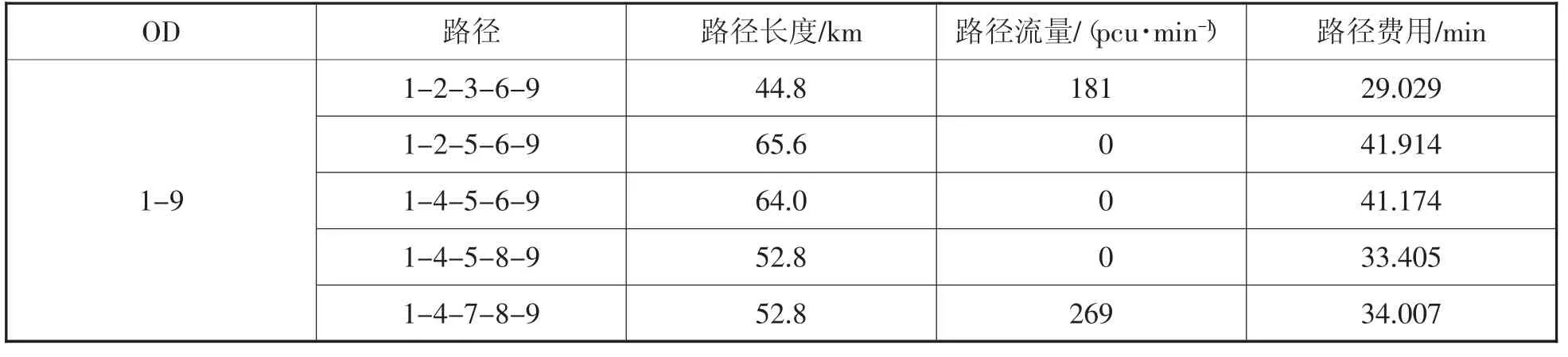
表3 路网中都是燃油汽车时的路径信息

在该路网中，只有一对OD 对，从获得的数据来看，在每次迭代结束后，进行下一次路径选择时，都会选择路径费用较少的路径。比如路网中2-3 路径费用9.056min，2-5 的路径费用12min，迭代后选择了2-3 路径，同理4-5 和4-7 选择了4-7 路径。因此进行迭代后路径选择都是选择费用最少的路径，而没有选择的路径其路径费用都是大于或者等于所选择的路径，因此所表现出来的情况符合Wardrop 第一原理。所以可知选取路段通行能力的期望值作为确定值，路段流量取其期望值进行讨论的做法是可行且合理的。

3.3 电动汽车路网交通分配

根据相关文献充电桩的分类，本文采用电池电量6kw，充电标准为240V、30A 的充电桩，其中节点4 和节点5 可各提供1 000 辆纯电动汽车进行充电。因此，目前每个节点的充电桩数量对于OD 数量来说是没有进行控制的。依据参考文献，本文所采用的纯电动汽车使用的充电电池最大电池容量为24kw 时，充电电池的消耗速率为0.3（kw·h）/km。另外，取纯电动汽车的固定充电时间为5min，充电时间系数为10min/（kw·h），纯电动汽车的初始电量为9kw·h。为了计算的方便，将纯电动汽车的驾驶员的焦虑里程设置为0。运用Matlab 软件进行编程求解，得到路网中各个路段费用、路段流量见表4，路径详细信息见表5，该路网总的行驶时间是104.297min。

表4 路网中都是电动汽车时的路段费用及路段流量

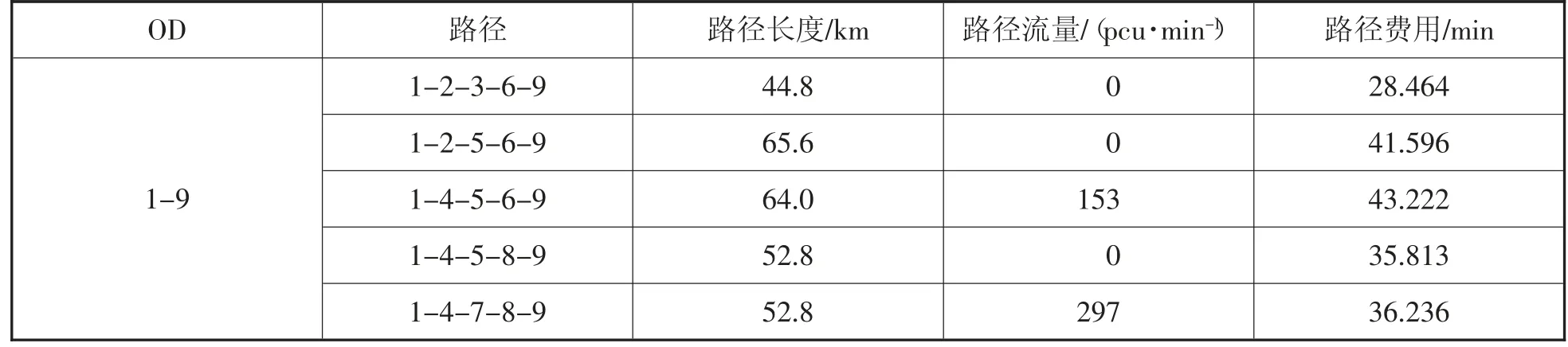
表5 路网中都是电动汽车时的路径信息

在该路网中，路网中的节点4 和节点5 作为安置充电桩的位置，因此这两个节点是起着承接的作用。从该路网的长度，以及电池的起始蓄电的电量来看，起点到终点在不充电的情况下是不可能完成的，所以必须在途中选择有充电桩的节点进行充电。因此最短路径要考虑到充电桩安置的位置以及充电时间，所以在该路网中节点4 和节点5 是必须选择的。在纯电动汽车的交通网络中，考虑到电动汽车充电的需求，以及受到路网中充电桩位置和数量的限制，在进行路径选择时，并不是选择路径费用最少的路径，而是要满足电池充电需求，足够支撑电动汽车从起点到终点的路径，因此所表现出来的情况不符合Wardrop 第一原理。

3.4 数据分析

燃油汽车网络和电动汽车网络的路径费用对比如图2 所示。

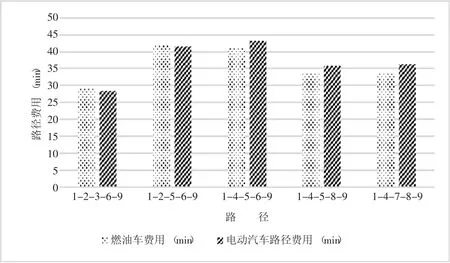
图2 数据对比图

从图2 数据分析可见，电动汽车在路网的行驶时间会大于普通燃油汽车在路网的行驶时间，所以这两种交通均衡分配问题是存在差异的。另外，从该路网中1-2-3-6-9 的路径费用来看，如果在电动汽车电量充足的情况下，普通燃油汽车和电动汽车选择的路线都是路径费用最少的，而没有选择的路径其路径费用都是大于或者等于所选择的路径，因此所表现出来的情况符合Wardrop 第一原理。但是当电动汽车电量不充足，在途中有充电需求时，电动汽车在路网中充电时间、充电桩位置以及数量都在影响着出行者对路径的选择，因此选择的最优路径并不是费用最少路径，而是能够完成出行需求的路径。

4 结 论

针对电动汽车在随机交通网络中出行的网络均衡问题，本文建立了考虑电动汽车出行时间随机性的交通网络均衡模型，并对电动汽车出行的随机行程时间和充电时间的线性组合问题进行了讨论，采用Matlab 软件进行了编程，并且运用了Frank-Wolfe 算法和K短路算法求解问题，获得了在路网中对交通均衡分配问题的一个数据结果的统计，验证了该模型和算法的正确性和可行性。结果表明：

（1） 在随机交通网络环境下，将路网中路段上的通行能力期望值认为是确定值，由于路段上交通流量会根据特殊情况不断变化，不易求解且反映不出路段上实际情况，于是对其进行了优化，采用交通流量的期望值，不仅便于计算，而且更精确地反映出纯电动汽车在路网中对路径的选择情况。

（2） 针对纯电动汽车特性的交通路网，考虑电动汽车行程时间随机特性，有助于研究电动汽车储蓄电池的蓄电能力；有助于观察电动车辆行驶状况，合理地布置充电桩的位置及数量；有助于未来对电动汽车的交通管理、分配、出行以及城市交通路网线路的布设，方便未来纯电动汽车的普及。

本文中只考虑了BPR 中对于交通阻抗的期望值研究，没有考虑纯电动汽车在充电时的充电时间期望，考虑纯电动汽车充电时间的期望问题需要进一步研究。