B2B 电子商务模式下多供货点智能配送VRP——以泉州为例

陈琳琳，杨 敏，程 春 CHEN Linlin, YANG Min, CHENG Chun

（1. 仰恩大学 管理学院，福建 泉州362014；2. 厦门大学 管理学院，福建 厦门361005）

(1. School of Management, Yangen University, Quanzhou 362014, China; 2. School of Management, Xiamen University, Xiamen 361005, China)

2019 年5 月28 日，福建永安国家棉花市场监测系统举办的棉花形势分析会上，福建纺织协会相关领导强调了福建要做好因地制宜、产业升级、区域分工协作。其中，物流供应链的改善和升级将成为产业升级的重点之一，直接影响产业的运营成本和效率。泉州作为福建省重要的纺织基地，其纺织鞋服发展迅速，随着“互联网+”战略的推进，出现越来越多的跨境电商企业，产业升级和创新发展迫在眉睫[1]。为促进传统纺织鞋服业在电子商务模式下更好的发展，本文以泉州纺织鞋业为例，基于目前泉州纺织鞋业在互联网环境下的发展现状，对其B2B 物流配送问题进行研究。

车辆路径（Vehicle Routing Problem, VRP） 作为物流供应链研究中的一大重要分支，目前已得到较多研究[2-6]。但是，关于B2B 电子商务模式下的VRP 研究则较少，已有研究多是关于B2C 电子商务模式下的VRP 进行探讨。Moons 等人研究了在B2C电子商务环境中整合订单拣选和车辆路线决策的价值[7]；Yuan 等人基于B2C 和O2O 订单的特点，提出一种创新的联合分销服务的车辆路径优化思路[8]；Chao 等人在B2C 电子商务模式下，基于实际城市道路系统的不完整图建立VRP 模型，并提出一种新的离散差分进化算法用于求解[9]；张晓楠等人以费用最小为目标，研究了模糊需求下的B2C 物流配送网络问题[10]；李琳等人针对B2C 电子商务环境下物流配送的特点建立带预约时间的VRP 模型[11]。此类基于B2C 电子商务模式下的VRP 模型多是考虑单仓库情形。

与B2C 电子商务模式下的单仓库VRP 情形不同，B2B 电子商务模式下的VRP 研究必然涉及多供货点、多需求点的问题，运输网络类似多仓库VRP 问题[12]。因此，本文将基于VRP 领域相关理论方法，对B2B 模式下的VRP 问题展开探讨，考虑VRP 模型的多仓库属性，相比于单仓库VRP，多仓库VRP 问题复杂度更高。本文以泉州纺织鞋业的B2B 发展为例，考虑多供货点、多需求点、时间窗等因素，从系统优化的角度，以降低资源消耗，提高整体效益为目标，构建适用于泉州纺织鞋业的B2B 电子商务模式下的多供货点VRP 模型，同时提出基于Python 和Gurobi 求解器的求解方法，最后通过仿真分析，从供货点集中和供货点分散两种情形，验证本文所提模型和求解方法的可行性和有效性，适用于泉州当前B2B 电子商务模式下的智能配送。

图1 泉州跨境电商微小企业运营模式

1 B2B 电子商务下物流配送模型

1.1 问题描述

泉州纺织鞋服产业发达，随着电子商务的发展，目前以个体工商户注册的跨境电商企业已逐渐增多。当商户收到跨境电商平台上的订单时，可在一手货源网平台先下单，后在线下进行提货发货，具体运营模式如图1 所示。一手货源网如爱搜鞋网，其线下店铺多分布在泉州幸福街附近。

本文所探讨的B2B 电子商务下的物流配送问题，正是基于泉州目前跨境电商背景下B2B 物流配送问题展开的。在泉州传统的B2B 电子商务模式下，未对物流配送工作做系统的规划，电子商务平台如爱搜鞋网主要用于商品的展示，买方商户下达订单后需要直接对自己的商品物流负责，由于快递费用较高，大部分买方商户选择自己上门取货，从系统优化的角度来看，往往会导致物流资源的浪费。基于此，本文构建多供货点多需求点的VRP 模型，从系统优化的角度，合理规划配送路线，在规定时间内完成需求点需求配送的同时，使物流资源利用率最大。

1.2 多供货点智能配送VRP 模型构建

为提高物流资源的利用率，本文将以物流集成商的角色，对物流配送问题进行优化。以每日需求为一个研究周期，考虑有m个供货点，n个需求点，K辆配送车辆，买方商户所需的商品为多品种商品，且各需求点的需求可能来自多个配送点，如图2 所示，某车辆执行一次配送任务的路径说明。

基于图2，对研究问题做进一步的研究假设：

（1） 车辆起止位置一致，起于配送中心，且终于配送中心；

（2） 所有车辆规模一致，保持行驶速度不变，且支持长途运输；

图2 车辆执行一次配送任务的路径示意图

（3） 车辆总数足够多，总能满足运载需求。

模型的相关参数定义如下：

P｛0,1,2,…,m+n+1 ｝节点集合，其中0 代表起点，m+n+1 代表终点；M= ｛1,2,…,m｝供货点集合；N=｛m+1,m+2,…,m+n｝送货点集合，i∈M,m+i∈N；K表示车辆总数；c表示运输的单位距离费用；dij表示路线（i,j）的距离；Fk车辆k一次启动费用，包括车辆折旧；Qk表示车辆k的最大装载容量；qj表示点j的需求量，若j∈M则qj为负，若j∈N则qj为正；v为车辆的行驶速度，假设保持匀速行驶；wik表示到达i节点时k车载有商品的量；tek表示车辆k的最早开始工作时间；tlk表示车辆k的最晚结束工作时间；ei表示节点i最早服务时间；li表示节点i最迟服务时间；si表示i需要的服务时间；hik表示车辆k在节点i的等待时间；rik表示车辆k到达节点i的时间。

决策变量：

以配送费用最小为目标构建模型如下：

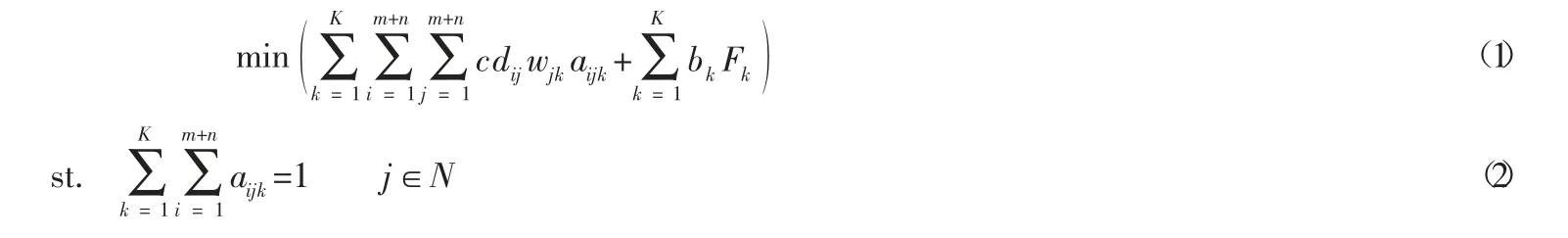
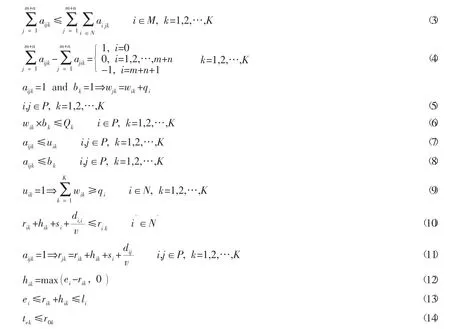
式（1） 为模型的目标函数，表示车辆的运输费用和启动费用最低。式（2） 保证每个需求点都能得到配送，为方便买方客户，设定买方客户的所有需求通过一次收货满足。式（3） 保证每次取货有对应的收货，其中N'为对应的需求点集合，如：点A, B, C 为点D 对应的需求点，则有从D 点出发的取货，至少应到达A, B, C 中的一个需求点。式（4） 为路径平衡约束，表示车辆有到达某点的路线，则对应会存在由该点发出的路线。式（5） 为货载量平衡约束，若车辆k经过路径i,（）j，i点为需求点，则车辆到达j点时的运载量为到达i点时的运载量减i点的需求量；若i为供货点，则车辆到达j点时的运载量为到达i点时的运载量加i点的取货量。式（6） 为最大装载限制约束。式（7） 和式（8） 满足货物与车辆匹配关系。式（9） 保证需求得到满足。式（10） 表示货物先取后送的约束。式（11） 表示时间平衡约束。式（12） 为等待时间约束。式（13） 为时间窗约束。式（14） 保证车辆起止时间有意义。

2 仿真分析

由最终模型可以看出，本文所构建的多仓库车辆路径优化模型是一个混合整数非线性规划模型，决策变量aijk，bk直接影响最终优化目标。为降低问题的复杂性，本文先设定运载车辆为统一规格，且每辆车仅需要完成一次配送任务，根据决策变量aijk和bk分两个阶段决策：确定调用车辆数目，确定车辆行驶路径。具体求解过程如图3 所示：

图3 模型求解过程图

为验证模型及求解方法的可行性和有效性，本文通过rand（）函数，随机生成6 个供货点，15 个需求点的运输网络。基于泉州纺织鞋业跨境电商的发展背景，供货点多集中在幸福街，而需求点则零散分布在大泉州地区，故在随机生成位置信息时，令供货点的位置信息限定在［0,1 0 ］范围内，而需求点的位置信息则分布在［0,100］范围内，随机产生的位置信息如表1 所示，其中第0 个点为车辆起始点，第23 个点为车辆终点。

假设车辆启动成本为500 元，车辆的行驶速度为50.4km/h，最大装载量为100 件，单位距离成本为6 元/km，车辆从原点出发完成货物配送后回到原点，提货开始时间和送货开始时间均为当天8 点，提货结束时间和送货结束时间均为当天18 点。订单相关信息如表2 所示，其中提货服务时间与提货量成正比。

基于上述数据，配送货物共计380 件，可确定bk的初始值为b1,b2,b3,b4=1，本文在Intel（R） Core（TM） i7-8565U CPU@1.80GHz 1.99GHz 处理器、8.00GB 内存、Windows 10（64 位） 系统下，运用Python 编码，调用Gurobi 求解器进行路径规划。求解结果如表3 所示，对应优化后的目标函数值为7 167.61，即初始总费用为7 167.61 元，对应配送路径图如图4 所示。

由表3 可得，车辆总是先到其任务配送路径上的所有供货点处取完货再逐一到对应需求点完成配送。分析可知，由于本文是基于泉州搜鞋网的B2B 模式特点展开的仿真分析，供货点较集中，因此，先全部取货再送货有利于缩短配送路径。最后，在需求时间窗允许的范围内，调整启动的配送车辆为2 辆，即通过同一车辆的多趟运输，进一步减少车辆启动费用，得调整后的总费用为6 167.61 元。

为进一步验证模型和求解方法的有效性，将供货点和需求点的位置信息重新随机生成，不对供货点做特别限定，所有位置皆在［0,100］内随机生成，其他需求信息不变。运行软件得到新的求解结果如图5 所示，总费用为7 974.32 元。

由图5 可得，此时，车辆的取货行为可能发生在配送中途，而位置相邻的需求点通常由同一配送路径完成，符合实际情况。

表1 位置信息

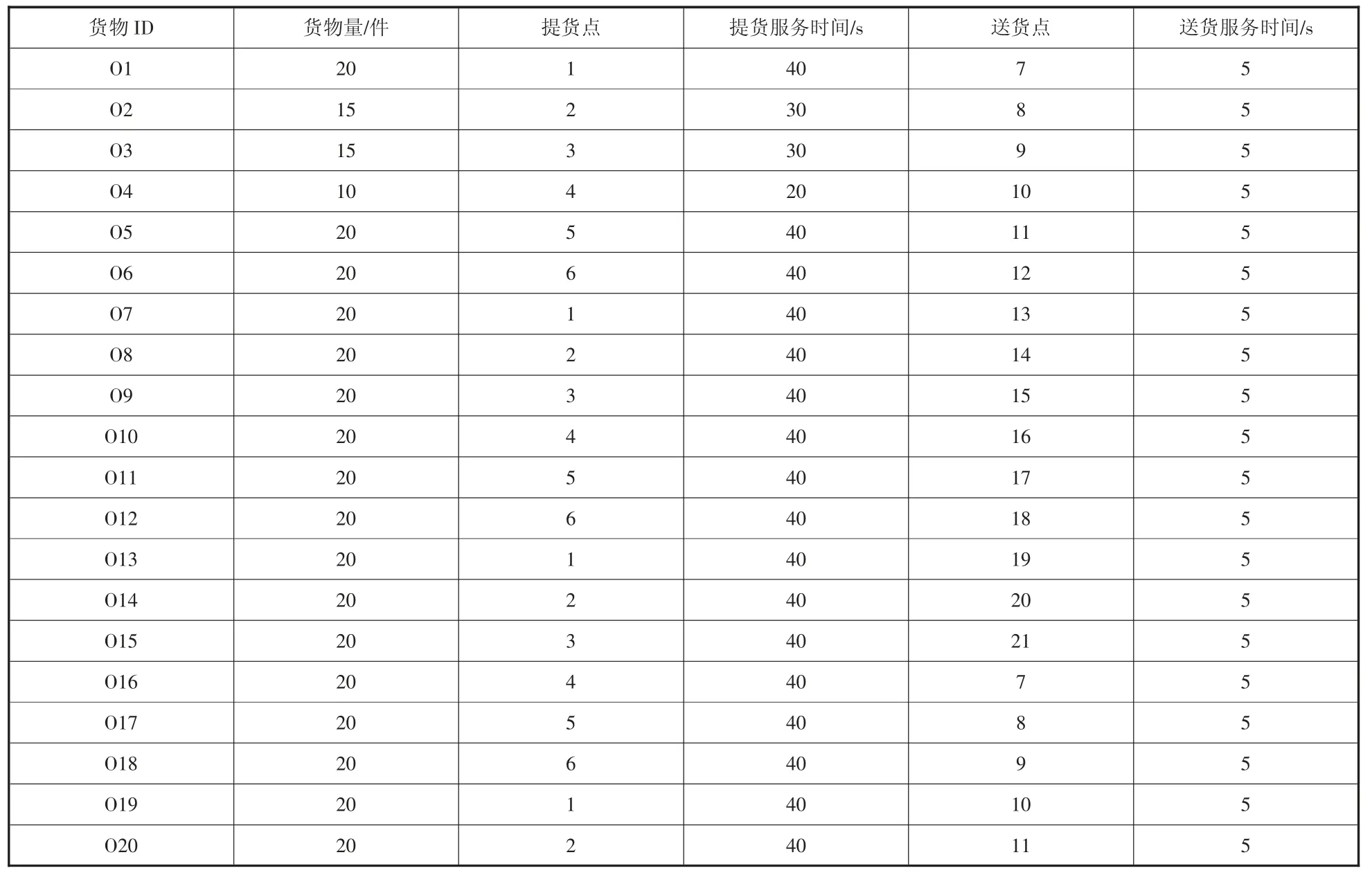
表2 订单信息

表3 供货点集中情况下的求解结果

综上，本文所提的数学模型和求解方法适用于B2B 模式下的多供货点智能配送问题研究，且算法运行时长均在30min 内，符合实际运营需要。在实际运营中，点与点间的距离数据可直接由商家信息和百度地图获取。相比于目前买方商户直接对商品物流负责的情形，本文从系统的角度统筹优化物流配送问题，明显有利于运输资源的节约。若买方商户各自进行商品取货则需要空载前往商品批发市场，而后返回，容易产生较多的车辆资源浪费；若买方商户选择“一件代发”操作，将商品交由第三方人员有偿代发，则容易造成较高的快递成本。而基于本文所提的多供货点智能配送模型，在充分考虑供需关系的同时，能够最大程度降低整体费用的支出，提高车辆利用率的同时，也间接减少了汽车尾气的排放。因此，在传统产业中考虑智能物流，统筹优化配送问题，将是未来的发展趋势，有利于产业升级。

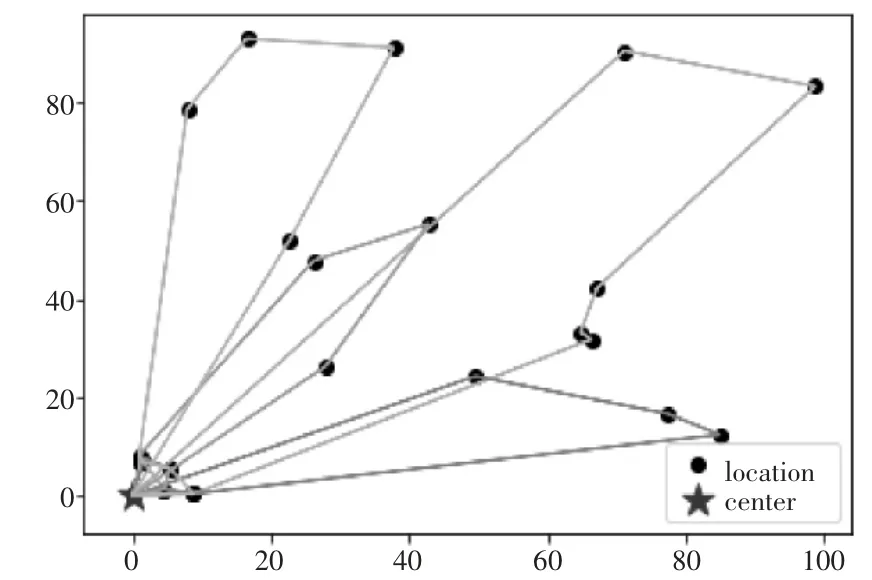
图4 供货点集中情况下的配送路径

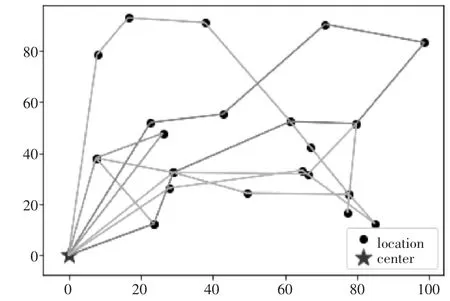
图5 供货点随机分布情况下的配送路径

3 结 论

本文针对B2B 电子商务模式下的VRP 问题，建立了多供货点智能配送VRP 模型。考虑车辆运输费用和启动费用，以总费用最小为目标，使得车辆资源得到充分利用；考虑多供货点多需求点的物流网络特点，提高模型在B2B 电子商务模式下的实际应用价值；并设计了基于Python 和Gurobi 求解器的求解方法，能够较快得到可行有效的配送方案。最后，基于泉州纺织鞋业目前跨境电商的发展特点，通过仿真实验，随机生成6 个供货点，15 个需求点，从供货点集中和分散两种情况分别探讨了智能配送问题。仿真结果表明，本文所提的模型和方法能够得到有效的配送方案，有利于资源的统筹优化，适用于解决B2B电子商务模式下的多供货点智能配送路径优化问题。以泉州目前传统纺织鞋业在B2B 电子商务环境下的发展现状为例，验证了统筹管理物流配送问题将进一步降低物流费用，促进传统产业在互联网环境下更好地发展。未来，将进一步考虑车辆规格不同、需求随机等情况下的配送问题，进一步提高模型的应用价值。