基于量子行为粒子群算法的航空瞬变电磁拟二维反演技术
2020-12-14何一鸣薛国强
何一鸣,薛国强,4*,赵 炀
(1.中国科学院地质与地球物理研究所 中国科学院矿产资源研究重点实验室,北京 100029; 2.中国科学院地球科学研究院,北京 100029; 3.中国科学院大学 地球与行星科学学院,北京 100049; 4.长安大学 地球物理场多参数综合模拟实验室(中国地球物理学会重点实验室),陕西 西安 710054)
0 引 言
航空瞬变电磁法发射和接收装置皆位于空中,完全摆脱了地形的限制,具有高效率和适应性强等特点,其广泛应用于矿产资源探测、地质填图和地热资源勘查等领域[1-7]。该方法在人工脉冲信号激发下产生感应电磁场响应,然后通过数据反演拟合重构地电信息。为获得更加接近地下真实模型的反演结果,研究精细反演算法显得极为必要。反演算法可划分为确定性反演算法和随机性反演算法,目前主流反演算法为确定性反演算法,例如广义逆矩阵[8]、共轭梯度[9]和拟牛顿[10]等确定性反演算法,具有计算速度快的特点,但是瞬变电磁法反问题具有非线性和病态性,以及确定性反演算法反演结果依赖于初始模型的选择等问题,在求解上述反问题时易受人为因素干扰陷入到局部极小值中,导致最终反演结果偏离真实参数模型[11]。随后,改进正则化方法被提出来,在确定性反演算法基础上加入模型约束来减小反演结果的非唯一性,同时提高反演结果的稳定性。其中Occam反演算法采用最大光滑稳定泛函所得到光滑反演结果能够保证电性变化上的连续性,但是对目标体边界刻画不够清晰[12];而聚焦反演算法采用最小梯度支撑稳定泛函得到尖锐反演结果能够显著提高目标体边界刻画精度,但是仍然存在假异常干扰。
随着近些年来计算科学的快速发展,随机性反演算法逐渐成为研究热点,主要包括粒子群(Particle Swarm Optimization,PSO)算法、模拟退火算法、遗传算法、贝叶斯算法和神经网络算法等[6,13-16]。其中粒子群算法作为一种群优化理论的随机性反演算法,具有较好的跳出局部极小值的能力,自从被提出后广泛应用于基因工程[17]、复合材料[18]、数学建模[19]、生命科学[20]等领域中。2006年,Fernandez-Alvarez等率先将其引入到地球物理反演中,成功地实现了垂直电测深的反问题求解[21]。最近十几年,众多学者先后开展了基于粒子群算法的反演研究工作,极大推动了粒子群算法在地球物理领域的发展,但是由于粒子群算法在求解非线性映射关系下的高维反问题时,仍然存在早熟收敛和收敛速度慢等问题,所以限制了粒子群算法在电磁法二、三维反演中的发展[15,22-24]。
本文首先分析了早熟收敛和收敛速度缓慢的原因,然后分别给出了相应的解决方案。一方面,在传统粒子群算法中,早熟收敛问题主要由于粒子群分布集中或运动随机性不足,使得各粒子快速向全局最优粒子聚集。本文引入量子行为粒子群(Quantum-behaved Particle Swarm Optimization,QPSO)算法改善传统的粒子群算法,其中引入量子在势阱中运动规律指导粒子群在空间位置更新,使得粒子可以出现在势阱范围内任何存在概率分布的位置上,进而能够克服群体聚集性导致的早熟收敛问题[25-26]。另一方面,局部极小值个数直接影响反演收敛速度,考虑到粒子群算法中局部极小值个数与模型参数的空间维度成指数正相关关系,因此,本文提出采用拟二维反演算法代替传统二维反演算法,将二维模型拆分为一维,设法提高粒子群算法的收敛速度[27]。但是在传统拟二维反演中,采用添加正则化项实现横向约束,如果在群体中开展基于L曲线法正则化参数寻优过程将要耗费大量计算资源[28]。结合量子行为粒子群算法中全局最优粒子在粒子群进化过程中的重要地位和积极影响,提出了采用非线性滑动窗口滤波器α-Trimmed方法开展全局最优粒子的模型参数光滑约束技术,实现粒子群算法的快速拟二维反演[29]。最后将量子行为粒子群算法拟二维反演技术应用到含噪全航空瞬变电磁数据处理中,反演结果更接近真实的地电模型参数,验证了算法有效性和鲁棒性,为全航空瞬变电磁反演解释提供一种合适的解释方法。
1 航空瞬变电磁法反问题
尽管航空瞬变电磁法不同装置形式之间存在一定差异,但原理上正反演问题都可以简要表述为
d=F(m)
(1)
式中:F是根据电磁传播规律建立的数学物理方程(正演算子);d为地表观测的响应数据;m为模型参数集。
在模型参数和正演算子已知的情况下,计算瞬变电磁响应是一个正问题。反之,如果观测数据和正演算子已知,那么推断地球内部结构或地下矿藏位置是一个典型的反问题。
用于求解反问题的反演算法可分为确定性反演算法[8-10]和随机性反演算法[13-16]。确定性反演算法[图1(a)]在模型空间中从某一个初始模型开始,沿着灵敏度函数确定的方向移动,当正演响应和记录的数据集之间的拟合差满足要求,即得到解,反演结果依赖于初始模型选取,易陷入局部最优解。而随机性反演算法[图1(b)]在整个模型空间内进行随机搜索,在模型空间中多个点同时开始,依据个体经验积累和群体的信息交流确定各个模型运动方向,且具有一定随机性,最后将所有满足拟合残差要求的模型组成表征反问题解的模型集,其中不仅包括一个全局最优解,还会有多个次优解,因此,随机性反演算法具有更强的全局寻优能力。

图1 确定性反演算法与随机性反演算法对比
2 方法原理
2.1 量子行为粒子群算法
粒子群算法是一种著名的群理论随机性反演算法,在1995年由Kennedy和Eberhart首次提出,灵感源自社会群体在自然界中搜索食物的过程,依据个体知识积累和群体信息共享为寻优运动过程提供指导,不断更新粒子群参数信息,最终获得最优解[30]。粒子的速度V和位置矢量X计算公式分别为
(2)
(3)

计算粒子群的目标函数ψ的表达式为
(4)
式中:N为数据个数;Dobs为拟合数据;d为仿真数据。
自从粒子群算法提出后,学者们先后提出了大量的改进算法,量子行为粒子群算法是其中之一[31-34]。在量子行为粒子群算法中,采用量子在多维空间中运动理论为粒子群位置更新提供指导,依据量子理论中势阱概念划分粒子运动范围,使得粒子可以出现在任何存在概率分布的位置上,进而能够克服传统粒子群算法中早熟收敛问题。量子行为粒子群算法的粒子群更新策略(图2)描述为

图2 量子行为粒子群算法示意图
(5)
(6)
(7)
(8)
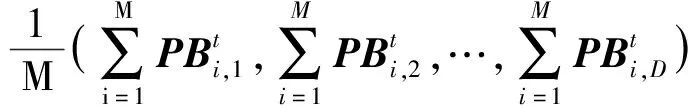
(9)
(10)
(11)
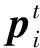
2.2 α-Trimmed方法横向约束
依据各测点对应的全局最优粒子对于所有其他粒子的空间约束力,提出采用α-Trimmed方法开展相邻测点的全局最优粒子间的横向模型约束。首先将各测点对应的全局最优粒子整合为一个最优模型矩阵mD,N,其中D为模型中变量数,N为测点个数。然后依据需要的横向约束尺度选择合适的固定窗宽n,滑动窗口读取矩阵数据,对选中的数据进行由小到大的排序得到新的序列
m(1∶D,αn+1+j)≤m(1∶D,αn+2+j)≤
…≤m(1∶D,n-αn+j)
(12)
式中:α为裁剪参数。
选择裁剪参数并裁掉序列中前段和后段相同数目的数据,最后将剩下的数据取平均值代替窗中心点的值[29],其表达式为
(13)
最后以N=5,α=0.25为例,给出了一个典型α-Trimmed方法处理流程,包括选区数据、排序、裁剪极值和求平均值等步骤。然后,通过滑动窗口对整体数据进行处理,实现横向约束效果(图3)。

图3 α-Trimmed方法的横向约束示意图
2.3 量子行为粒子群拟二维反演算法计算步骤
量子行为粒子群拟二维反演算法计算步骤(图4)如下:
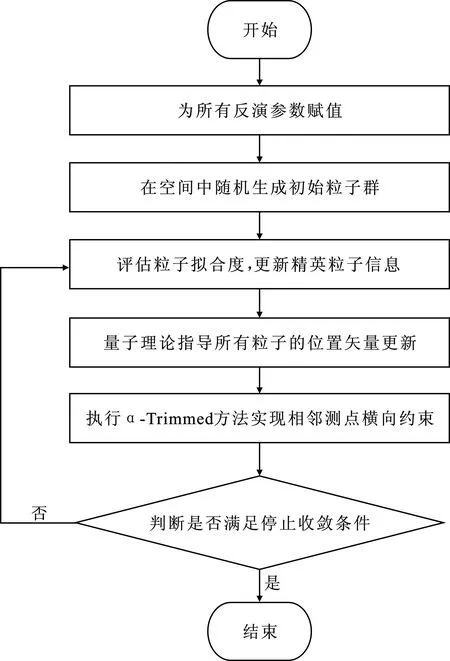
图4 量子行为粒子群算法拟二维反演流程
步骤1,获取Nobs个测点的响应数据和收发装置参数。
步骤2,设置反演参数。
步骤4,计算第N个测点所有粒子的适应度,依据式(5)~(9)更新各测点粒子群最优解和全局最优解。
步骤5,根据式(5)~(8)依次计算第N个测点能量势阱的中心位置、能量势阱范围和平均最优值,再计算创造力因子,并根据式(4)更新粒子群的位置信息。
步骤6,计算第N个测点所有粒子的适应度,然后更新粒子群最优解和全局最优解。
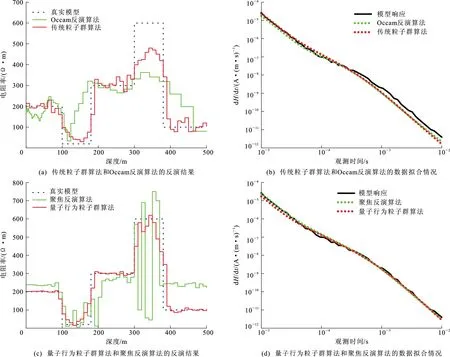
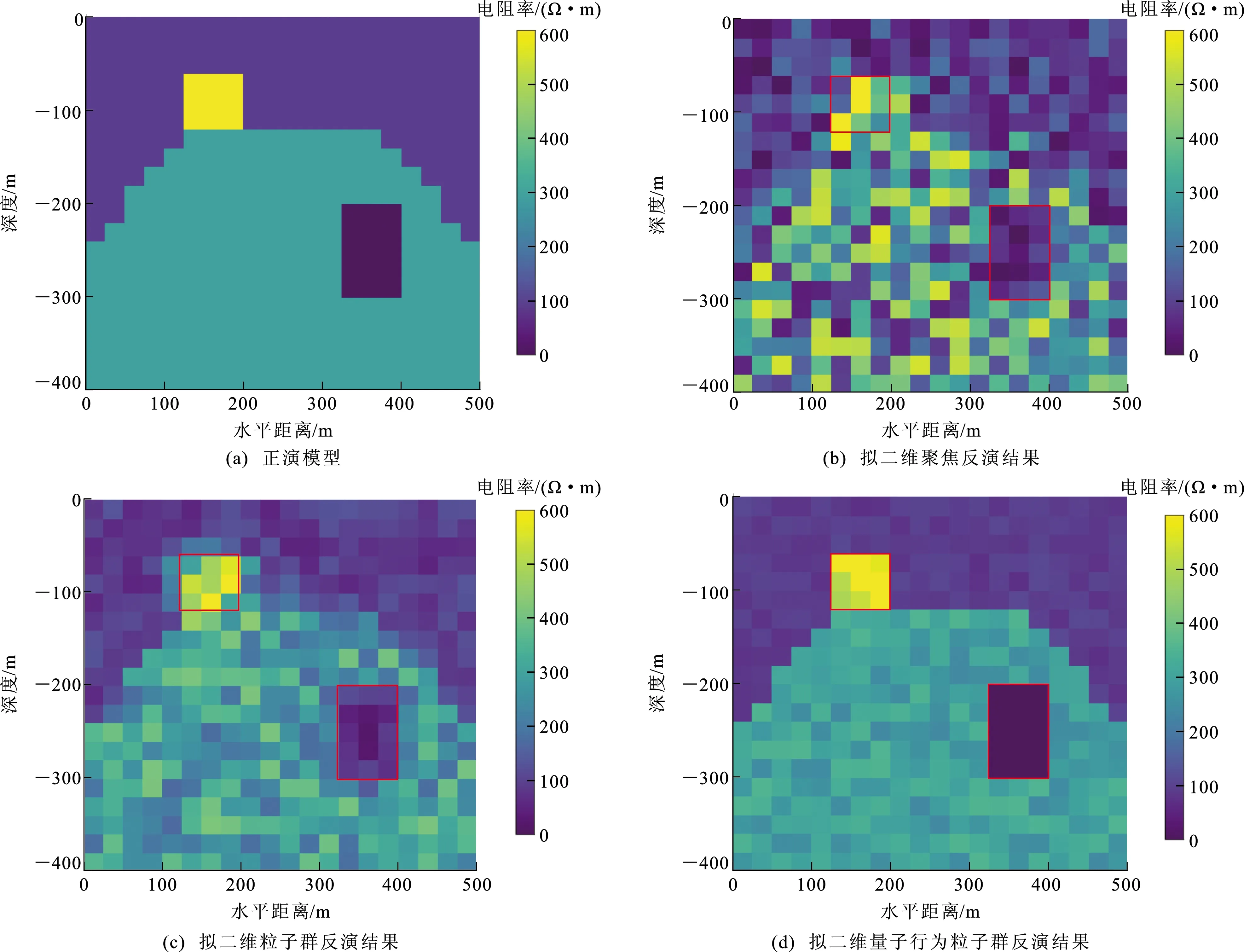
步骤7,如果N 步骤8,利用各测点全局最优解生成最优模型矩阵,并设为外部存档集。 步骤9,开展α-Trimmed方法横向约束,然后更新各测点粒子群最优解和全局最优解,t=t+1。 步骤10,如果t≤T,N=1,返回步骤4,否则输出全局最优解作为最终拟二维反演解。 在一维反演中,仿真模拟的地质模型由5层构成,由上到下各层电阻率和层厚度参数分别为[200,20,300,600,100]和[100,80,120,80]。其中发射波形为25 Hz双极性方波,电流大小为1 A,线圈半径为25 m,离地高度为30 m,记录时间道为0.001~10.000 ms,接收点位于发射线圈中心,观测磁场强度垂直分量的时间导数(dH/dt)响应曲线,添加随机噪声后信噪比达到26 dB。 为检验量子行为粒子群算法跳出局部最优解的能力,对比了在相同拟合差条件下,两种主流的正则化约束反演算法(Occam反演算法和聚集反演算法)与传统粒子群算法和量子行为粒子群算法寻优效果对比。传统粒子群算法和Occam反演算法的反演结果[图5(a)]表明Occam反演算法中提取异常体的边界信息较为困难,而传统粒子群算法能够更好地刻画边界信息。量子行为粒子群算法和聚焦反演算法的反演结果[图5(c)]表明聚焦反演算法对于边界信息更敏感,但是存在过多的假异常。在量子行为粒子群算法的一维反演结果中,在100~190 m深度观察到低阻层,最小电阻率为8 Ω·m;在310~380 m深度观察到高阻层,最大电阻率为616 Ω·m。量子行为粒子群算法反演结果更加接近真实地质模型,有效压制了反问题的非唯一性。在相同拟合差条件下,量子行为粒子群算法搜索精度高于目前主流的反演算法。 图5 基于5层地电模型的反演拟合图 在模型参数设置中,层数为50层,厚度参数固定,粒子数为200,最大迭代次数为50。Occam反演算法和聚焦反演算法初始模型为100 Ω·m的半空间模型;传统粒子群算法初始模型在搜索空间中随机生成,自我认知系数和社会认知系数取值均为2;量子行为粒子群算法中的创造力参数取值为[0.5,1.0],随迭代次数线性递减变化,实现反演早期大范围全局搜索和反演晚期局部精细搜索。 在拟二维反演算法研究中,地质模型背景电阻率为上、下两层,分别为100和300 Ω·m。如图6(a)所示,在浅部和深部分别设计一个60 m×60 m的正方形高阻异常体和一个100 m×60 m长方形低阻异常体。其中,发射波形为25 Hz双极性方波,电流为1 A,线圈半径为15 m,发射线圈和接收点的离地高度分别为45和50 m,记录时间道为0.1~10.0 ms,接收磁感应强度垂直分量的时间导数(dB/dt)响应曲线。在25 m点距的500 m剖面上共包括21个测点。响应数据如图7(a)所示,浅部异常体位置和深部异常体位置对应的数据早期测道变化都明显。为了测试量子行为粒子群算法的鲁棒性,在得到的原始数据中加入高斯随机噪声,使信噪比达到26 dB[图7(b)]。 图6 电阻率剖面 图7 多测道图 模型参数反演计算中分别开展了基于L曲线法拟二维聚焦反演和基于α-Trimmed方法的拟二维粒子群反演。α-Trimmed方法经过50次迭代计算后,各算法的反演结果如图6所示。图6(b)和(c)反演结果表明,与聚焦反演算法相比,粒子群算法反演结果中包括更少的假异常,更接近真实地电模型。对比图6(c)和(d)反演结果,量子行为粒子群算法显著改善了反演结果的精度。上述实验验证了基于量子行为粒子群算法的航空瞬变电磁法拟二维反演技术的有效性和鲁棒性。其中,α-Trimmed方法的参数N=5,5点平滑既能保证横向连续又不会丢失真实地电信息;裁剪参数设置为α=0.25,去除模型参数中的极值,保证了反演结果稳定性。 (1)首先从理论上分析了传统粒子群算法在高维反演中存在早熟收敛和速度缓慢等问题的原因,然后结合前人改进粒子群算法的技术和航空瞬变电磁反演问题特点,提出了基于量子行为粒子群算法与α-Trimmed方法相结合的拟二维反演技术,拟克服了早熟收敛和反演速度缓慢问题。 (2)经过一维和二维数值模拟分析,结果表明:无论是在相同拟合差条件下,还是相同迭代次数下,量子行为粒子群算法都能够提供更接近真实的地电模型反演结果,算法的可靠性和鲁棒性得到了验证。 (3)目前粒子群反演算法的实际计算速度仍大幅落后于传统的确定性反演算法,下一步计划开展关于粒子群反演算法和确定性反演算法的混合算法,将已成熟应用于电磁法反演中的确定性反演算法与粒子群算法相结合,希望能够获得更高精度、更快速度的混合算法,在更大的搜索空间中开展拟三维航空瞬变电磁反演研究。3 数值模拟
3.1 一维反演
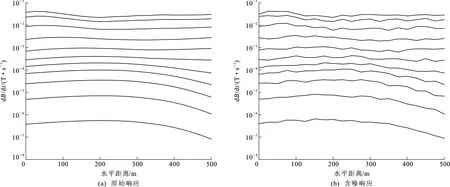
3.2 拟二维反演
4 结 语
